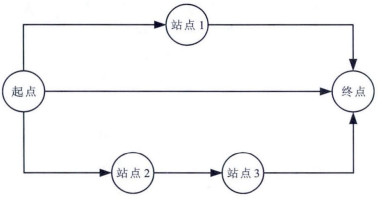
-
摘要: 针对中国大城市的工作生活模式与公交网络的特性, 以成都市居民公交出行为研究对象, 提出了符合乘客路径选择行为的广义公交路径。考虑了公交出行的路段阻抗和站点阻抗, 建立了公交路径阻抗函数, 提出了有效路径的确定方法。基于改进的Logit模型, 建立了一种换乘行为影响下的路径选择模型。以成都市部分公交网络为例, 应用提出的配流算法进行实例验证。分析结果表明: 当选定的4条公交线路高峰时段的最小发车间隔分别为4、4、3、3min, 非高峰时段的最大发车间隔均为10min时, 对应的最小换乘步行时间和最大换乘步行时间分别为0、6min; 当最大路径阻抗和最小路径阻抗分别为71.5、51.5min时, 对应的乘车时间分别为60、48min, 路径选择比例分别为5.53%、41.98%;当最大路径阻抗和最小路径阻抗分别为52.5、48.5min时, 对应的乘车时间分别为42、39min, 路径选择比例分别为13.40%、62.07%;考虑换乘行为时, 配流结果与实际值的最大相对误差、最小相对误差和平均相对误差分别为16.46%、11.09%、14.42%, 不考虑换乘行为时, 最大相对误差、最小相对误差和平均相对误差分别为34.37%、11.38%、23.15%。考虑换乘行为的配流结果更贴近实际情况。Abstract: Aiming at the work and life modes and the particularities of public traffic networks of big cities in China, the public traffic trip behaviors of residents in Chengdu City were taken as study object, and the generalized public traffic route which could accord with the route choice behavior of passenger was put out.By considering the section impedance and station impedance during the public traffic trip, the impedance function of public traffic route was set up, and the determination method of effective path was proposed.Based on the improved logit model, a route choice model under the influence of transfer behavior was established.The part public traffic network of Chengdu City was taken as an example, the example verification was carried out by using proposed assignment algorithm.Analysis result indicates that when the minimum departure intervals of four designate public traffic lines during peak period are 4, 4, 3, 3min respectively and all the maximum departure intervals during non-peak period are 10min, the minimum and maximum transfer walking times are 0, 6 min respectively.When the maximum impedance and minimum impedance are 71.5, 51.5min respectively, the riding times are 60, 48min respectively, the route choice ratios are 5.53%, 41.98% respectively.When the maximum impedance and minimum impedance are 52.5, 48.5 min respectively, the riding times are 42, 39 min respectively, the route choice ratios are 13.40%, 62.07% respectively.When the transfer behavior is considered, the maximum relative error, the minimum relative error and the average relative error of assignment results and actual values are 16.46%, 11.09%, 14.42% respectively.When the transfer behavior is not considered, the maximum relative error, the minimum relative error and the average relative error are 34.37%, 11.38%, 23.15% respectively.The public traffic assignment result considering transfer behavior is in accord with actual situation.
-
图 9 不同有效路径容忍系数对配流结果的影响
Figure 9. Influences of different values of Eon public traffic assignment results
图 10 不同路网熟悉程度对配流结果的影响
Figure 10. Influences of different values ofθon public traffic assignment results
-
[1] NUZZOLO A, CRISALLI U, ROSATI L. A schedulebased assignment model with explicit capacity constraints for congested transit networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 20 (1): 16-33. doi: 10.1016/j.trc.2011.02.007 [2] CIPRIANI E, GORI S, PETRELLI M. Transit network design: aprocedure and an application to a large urban area[J]. Transportation Research Part C: Emerging Technologies, 2012, 20 (1): 3-14. doi: 10.1016/j.trc.2010.09.003 [3] WAHBA M. MILATRAS: microsimulation learning-based approach to transit assignment[D]. Toronto: University of Toronto, 2008. [4] 雷全胜, 唐祯敏. 城市公交平衡配流研究的几个关键问题综述[J]. 系统工程学报, 2003, 18 (1): 62-66, 70. doi: 10.3969/j.issn.1000-5781.2003.01.010LEI Quan-sheng, TANG Zhen-min. Several key problems about the study of equilibrium assignment for urban transit network: a survey[J]. Journal of Systems Engineering, 2003, 18 (1): 62-66, 70. (in Chinese). doi: 10.3969/j.issn.1000-5781.2003.01.010 [5] 陈鹏, 严新平, 李旭宏, 等. 轨道交通与常规公交换乘优惠模型[J]. 长安大学学报: 自然科学版, 2011, 31 (5): 85-90. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201105017.htmCHEN Peng, YAN Xin-ping, LI Xu-hong, et al. Transfer benefit model between rail transit and bus transit[J]. Journal of Chang'an University: Natural Science Edition, 2011, 31 (5): 85-90. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201105017.htm [6] 王镜, 邵春福, 毛科俊. 公交换乘优惠的双层规划模型[J]. 中国公路学报, 2008, 21 (2): 93-97. doi: 10.3321/j.issn:1001-7372.2008.02.018WANG Jing, SHAO Chun-fu, MAO Ke-jun. Bi-level programming model for transfer benefit of public transportation[J]. China Journal of Highway and Transport, 2008, 21 (2): 93-97. (in Chinese). doi: 10.3321/j.issn:1001-7372.2008.02.018 [7] YU Bin, YANG Zhong-zhen, JIN Peng-huan, et al. Transit route network design-maximizing direct and transfer demand density[J]. Transportation Research Part C: Emerging Technologies, 2012, 22 (10): 58-75. [8] KNOPPERS P, MULLER T. Optimized transfer opportunities in public transport[J]. Transportation Science, 1995, 29 (1): 101-105. doi: 10.1287/trsc.29.1.101 [9] SHAFAHI Y, KHANI A. A practical model for transfer optimization in a transit network: model formulations and solutions[J]. Transportation Research Part A: Policy and Practice, 2010, 44 (6): 377-389. doi: 10.1016/j.tra.2010.03.007 [10] ANEZ J, BARRA D L, PEREZ B. Dual graph representation of transport networks[J]. Transportation Research Part B: Methodological, 1996, 30 (3): 209-216. doi: 10.1016/0191-2615(95)00024-0 [11] JOLLIFFE J K, HUTCHINSON T P. A behavioural explanation of the association between bus and passenger arrivals at a bus stop[J]. Transportation Science, 1975, 9 (3): 248-282. doi: 10.1287/trsc.9.3.248 [12] LOZANO A, STORCHI G. Shortest viable path algorithm in multimodal networks[J]. Transportation Research Part A: Policy and Practice, 2001, 35 (3): 225-241. doi: 10.1016/S0965-8564(99)00056-7 [13] POON M H, WONG S C, TONG C O. A dynamic schedulebased model for congested transit networks[J]. Transportation Research Part B: Methodological, 2004, 38 (4): 343-368. doi: 10.1016/S0191-2615(03)00026-2 [14] 翁敏, 毋河海, 杜清运, 等. 基于公交网络模型的最优出行路径选择的研究[J]. 武汉大学学报: 信息科学版, 2004, 29 (6): 500-503. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH200406007.htmWENG Min, WU He-hai, DU Qing-yun, et al. An optimal route choice based on public traffic network model[J]. Geomatics and Information Science of Wuhan University, 2004, 29 (6): 500-503. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH200406007.htm [15] 赵巧霞, 马志强, 张发. 以最小换乘次数和站数为目标的公交出行算法[J]. 计算机应用, 2004, 24 (12): 136-137, 146. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY200412046.htmZHAO Qiao-xia, MA Zhi-qiang, ZHANG Fa. Algorithms for public transit trip with minimal transfer times and stops[J]. Computer Applications, 2004, 24 (12): 136-137, 146. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY200412046.htm [16] 苏爱华, 施法中. 公交网络换乘问题的一种实现[J]. 工程图学学报, 2005 (4): 55-59. https://www.cnki.com.cn/Article/CJFDTOTAL-GCTX200504010.htmSU Ai-hua, SHI Fa-zhong. Optimal route choice of public traffic network based on shortest path searching[J]. Journal of Engineering Graphics, 2005 (4): 55-59. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCTX200504010.htm [17] 侯刚, 周宽久. 基于换乘次数最少的公交网络最优路径模型研究[J]. 计算机技术与发展, 2008, 18 (1): 44-47. https://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ200801013.htmHOU Gang, ZHOU Kuan-jiu. Research for public traffic network model of optimum route with minimal transfer times[J]. Computer Technology and Development, 2008, 18 (1): 44-47. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ200801013.htm [18] 刘剑锋. 基于换乘的城市轨道交通网络流量分配建模及其实证研究[D]. 北京: 北京交通大学, 2012.LIU Jian-feng. Transfer-based modeling flow assignment with empirical analysis for urban rail transit network[D]. Beijing: Beijing Jiaotong University, 2012. (in Chinese). [19] 董治, 李林波, 王艳丽. 城市交通管理公众参与机制的要素[J]. 长安大学学报: 社会科学版, 2009, 11 (1): 38-41, 49. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200901009.htmDONG Zhi, LI Lin-bo, WANG Yan-li. Elements in public participation mechanism of urban traffic management[J]. Journal of Chang'an University: Social Science Edition, 2009, 11 (1): 38-41, 49. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200901009.htm [20] 李淑庆, 李哲, 朱文英. 一体化公交网络均衡配流模型[J]. 交通运输工程学报, 2013, 13 (1): 62-69. http://transport.chd.edu.cn/article/id/201301010LI Shu-qing, LI Zhe, ZHU Wen-ying. Equilibrium assignment model of integrated transit network[J]. Journal of Traffic and Transportation Engineering, 2013, 13 (1): 62-69. (in Chinese). http://transport.chd.edu.cn/article/id/201301010 [21] LAM W H, HUANG Hai-jun. A combined trip distribution and assignment model for multiple user classes[J]. Transportation Research Part B: Methodological, 1992, 26 (4): 275-287. [22] 石琼, 吴群琪. 拥挤收费为主导缓解城市交通拥挤可行性研究[J]. 长安大学学报: 社会科学版, 2004, 6 (3): 38-42. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200403010.htmSHI Qiong, WU Qun-qi. Feasibility research on congestion pricing for our urban traffic congestion[J]. Journal of Chang'an University: Social Science Edition, 2004, 6 (3): 38-42. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200403010.htm [23] 王元庆, 王瑶文, 孙传姣. 城市交通技术援助项目特点及效果[J]. 长安大学学报: 社会科学版, 2008, 10 (1): 38-42. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200801010.htmWANG Yuan-qing, WANG Yao-wen, SUN Chuan-jiao. Characteristics of technical assistance for urban transportation and effect[J]. Journal of Chang'an University: Social Science Edition, 2008, 10 (1): 38-42. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200801010.htm [24] 赵建有, 俞礼军. 城市交通可持续发展状态量化评价方法[J]. 长安大学学报: 自然科学版, 2004, 24 (4): 63-66. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200404015.htmZHAO Jian-you, YU Li-jun. Quantitative assessment method of sustainable development state for urban transport system[J]. Journal of Chang'an University: Natural Science Edition, 2004, 24 (4): 63-66. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200404015.htm -
下载:
点击查看大图
图(10) / 表(2)
计量
- 文章访问数: 676
- HTML全文浏览量: 109
- PDF下载量: 1186
- 被引次数: 0
