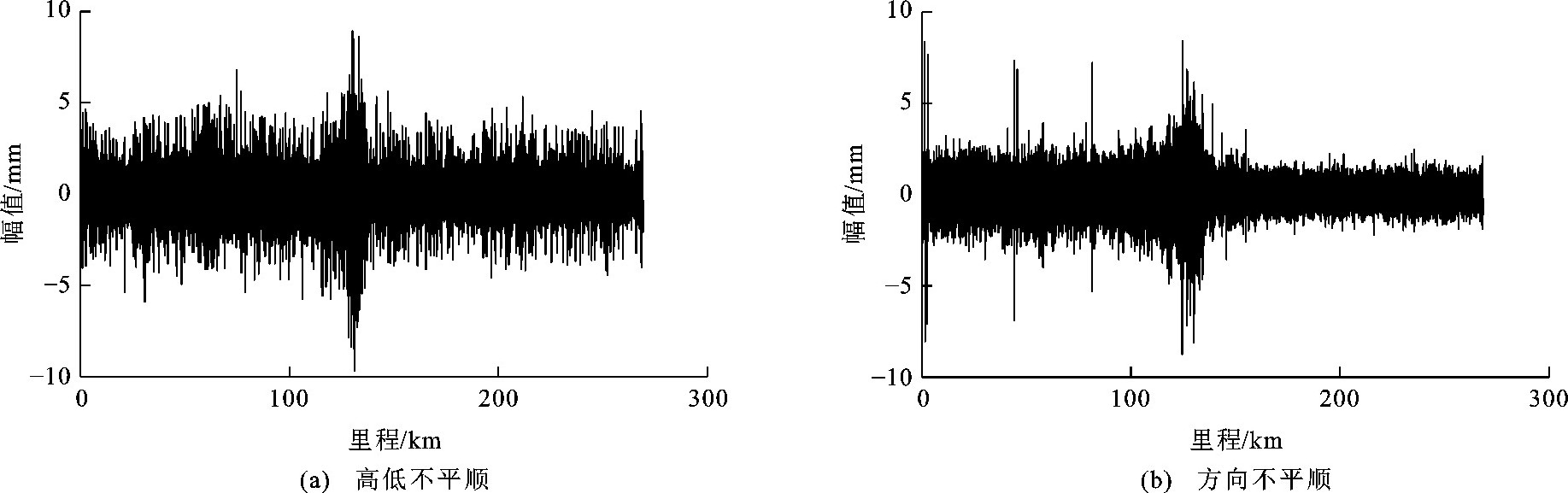
Abstract: To efficiently select track irregularity random samples for satisfying the ergodicity requirements of excitation sources in stochastic dynamics and reliability analysis in vehicle-track system, the weak-stationarity and similarity spectral of track irregularities were introduced to propose a track irregularity probabilistic model. Using the discrete probability integration and statistical approaches, the massively measured track irregularity time histories were divided into multiple time-domain sequences. The statistical power spectral density distribution of each sequence was calculated by the spectral analysis method. Then, using the matrix-based method, the set representation of the power spectral density function of track irregularities was obtained. It was assumed that the power spectral densities could be linearly accumulated at different frequencies, allowing the probabilities of entire spectra line to be obtained using the power spectral density probability distribution of a single frequency. The representative track irregularity spectra were selected through the commonly random simulation methods, and the track random irregularities were inversely simulated. The height and direction track irregularities of high-speed railway about 269 km were measured. Based on the vehicle-track coupled dynamics theory, the calculation results between the track irregularity probabilistic model and track irregularity stochastic model was compared from the aspects of the simulated amplitude of track irregularity and the probability density distribution for dynamic response in the vehicle-track system to verify the validity and high efficacy of the track irregularity probabilistic model. Calculation result shows that when taking the track random irregularities caused by the two models as excitation sources, the difference of the obtained probability entropies of vehicle-track system dynamic response between the two models is less than 2%. Both models can accurately express the excitation characteristics of track irregularities. The stochastic and probabilistic models need 131 and 33 random samples, respectively, to guarantee the consistent probability density distributions between the simulation and measurement, and the probabilistic model has higher computation efficiency. Under the presented computational condition, the wheel-rail forces and car body accelerations are 38-152 kN and-0.042 g-0.043 g, respectively, and are respectively less than the limits of wheel-rail forces (170 kN) and car body accelerations (0.25 g) in Code for High Speed Railway Design (TB 10621—2014). The track irregularity status of the investigated high-speed line is sufficient to guarantee the running safety and riding comfort of the vehicle.