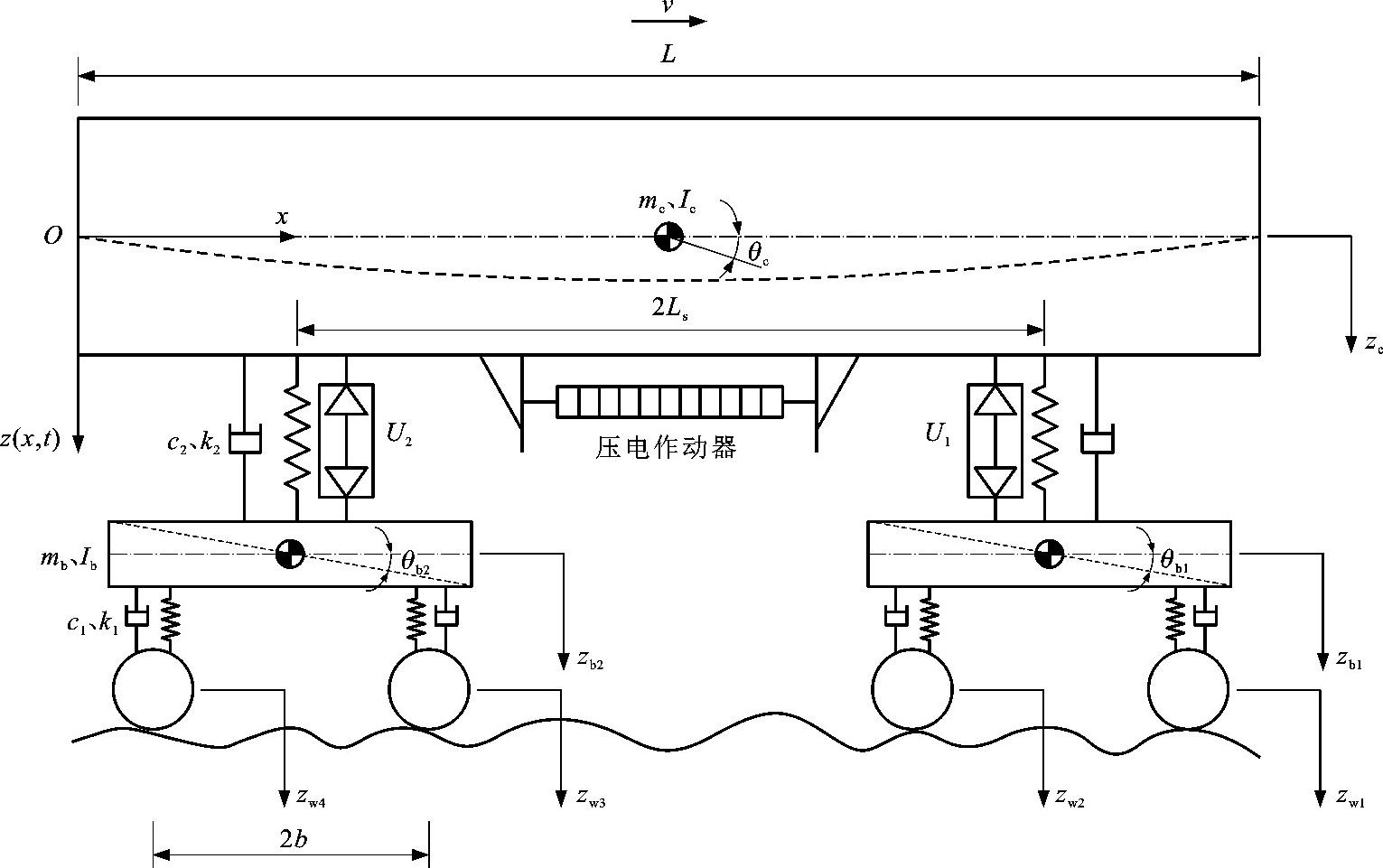
Vibration control of EMU car body based on secondary vertical actuators and piezoelectric actuators
-
摘要: 为了减小高速动车组车体刚性与弹性振动, 提出了一种基于二系垂向作动器与车体压电作动器的高速动车组车体振动主动控制方法; 基于某型高速动车组, 设计了一种在车辆二系安装垂向作动器, 在车体底架布置压电作动器, 运用H∞鲁棒最优控制器进行车辆协调控制的主动减振方法; 建立了基于车辆动力学参数的刚柔耦合减振力学模型, 采用H2及H∞准则优化压电作动器与压电传感器布置位置, 运用鲁棒最优控制方法设计了H∞反馈控制器; 利用MATLAB仿真了减振装置与主动控制方法对车辆动力学性能的影响, 比较了被动悬挂车辆、仅安装二系垂向作动器车辆与采用主动控制车辆的动力学性能差异。研究结果表明: 压电作动器与压电传感器布置在距车体左端距离为7.15、12.25、17.35m处车体一阶及二阶弹性模态归一化H2及H∞范数最大, 可以作为压电作动器与传感器的布置位置; 基于二系垂向作动器与车体压电作动器的鲁棒最优控制方法能够有效地抑制车体的振动, 一阶垂弯振动频率处车体中部和转向架上方的加速度功率谱分别减小为被动悬挂车辆的5%、10%;速度越大, 振动加速度抑制效果越明显, 当车辆的运行速度为200km·h-1时, 车体振动加速度均方根减小10%, 当车辆的运行速度为350km·h-1时, 车体振动加速度均方根减小18%;相对于被动悬挂, 二系垂向作动器输出力功率谱在车体浮沉与点头振动频率处的量级为106 N2·Hz-1, 对车体刚性振动有较大抑制作用, 压电作动器电压功率谱在车体一阶垂弯振动频率处达到峰值4 000V2·Hz-1, 对车体弹性振动有较大抑制作用。Abstract: To reduce the rigid and elastic vibration of car body of high-speed electric multiple units (EMU), the active vibration control method was proposed based on secondary vertical actuators and car body piezoelectric actuators. Based on a certain type of high-speed EMU, an active reducing method of vibration was designed in which vertical actuators were installed in thesecondary suspension, piezoelectric actuators were arranged in the under-frame of the car body, and an H∞ robust optimal controller was used to coordinate the vehicle control. A mechanics model of rigid-flexible coupled vibration reduction based on vehicle dynamics parameters was established. The placement positions of the piezoelectric actuators and sensors were optimized by using the H2 and H∞ norms. The H∞ feedback controller was designed by robust optimal control method. The effect of vibration damper and active control method on vehicle dynamic performance was simulated by MATLAB. The dynamic performance differences between passive suspension vehicle, secondary vertical actuators vehicle and active control vehicle were compared. Analysis results show that when the piezoelectric actuators and the piezoelectric sensors are arranged at the distances of 7.15, 12.25, and 17.35 mfrom the left end of the car body, the normalized H2 and H∞ norms of the first and second-order elastic modes of the car body are the largest, and can be used as the placement positions of piezoelectric actuators and sensors. The robust optimal control method based on the secondary vertical actuators and car body piezoelectric actuators can effectively suppress vibration of the car body, and the acceleration power spectrums of the first order vertical bending vibration frequency on the car body centre and above the bogie reduce by 5% and 10% of passive suspension vehicle, respectively. With higher velocity, the vibration acceleration suppression effect is more obvious. When vehicle's speed is 200 and 350 km·h-1, its mean square root of vibration acceleration decreases by 10% and 18%, respectively. Compared with the passive suspension, the magnitudes of output force power spectrums of the secondary vertical actuators are 106 N2·Hz-1 at the bounce and pitch vibration frequencies of the car body. Thus, the secondary vertical actuators can greatly suppress the rigid vibration of the car body. The voltage power spectrums of the piezoelectric actuators reach a peak of 4 000 V2·Hz-1 at the first order vertical bending vibration frequency of the car body, which greatly suppresses the elastic vibration of the car body.
-
0. 引言
在高速铁路动车组设计中, 速度是设计的终极目标, 安全是设计的永恒主题。为了提高动车组运行速度, 降低运行过程中的能量消耗, 在车体设计过程中采用铝合金代替不锈钢, 用“三明治夹心”结构代替实体结构, 这种轻量化设计导致车体刚度减小, 自振频率降低。同时, 随着运行速度的提高, 线路激扰频率增大; 而随着车辆服役时间和环境的变化, 轮轨接触产生的激扰力也会变化, 从而引起车体运行过程中的弹性振动[1, 2, 3]。该振动频率处于人体敏感的频率范围, 影响乘坐舒适性, 同时也导致车体与车下设备的振动失效问题[4]。
为了抑制车体的振动, 国内外学者做了大量的研究。黄彩虹等将高阻尼弹性材料贴附于车体适当部位, 通过提高车体结构阻尼, 增加车体结构损耗因子方法, 达到减小车体弹性振动, 提高乘坐舒适性的目的[5, 6]; Schandl等在地铁车辆车体底架侧梁适当部位安装压电作动器, 采用鲁棒反馈控制方法控制车体振动, 通过仿真及比例模型试验验证了方法的有效性[7, 8]; Foo等在车体二系悬挂处安装电液作动器, 在车体中部安装电磁作动器, 采用天棚阻尼控制方法, 减小了车体轻量化设计引起的弹性振动[9]; Sugahara等为了提高乘坐舒适性, 降低刚性与垂向弯曲振动, 采用在车辆一系垂向悬挂处安装可调阻尼减振器, 在二系悬挂处安装可调阻尼空气弹簧, 运用天棚阻尼控制方法降低车体振动, 仿真与新干线试验表明, 采用该方法的车辆一阶垂弯振动加速度功率谱可降低至原来的20%, 刚体振动加速度功率谱降至原来一半[10, 11]。
由于一阶垂向弯曲弹性振动对车体弹性振动贡献最大[12, 13, 14], 而二系垂向可调阻尼减振器设置在车体一阶垂向弹性振动的节点附近, 因此, 仅对车体刚性振动减振效果明显, 对车体弹性振动减振效果有限。随着压电智能结构制造工艺的提升, 其输出力可满足车体这类大型结构弹性振动控制时对工作力的要求[15, 16, 17, 18, 19], 而且压电智能结构具有质量轻、能耗低的优点, 对柔性结构振动有较好的抑制作用。
本文针对高速动车组运营过程中出现的车体共振问题, 提出一种二系布置垂向作动器与车体布置压电作动器, 采用鲁棒最优控制方法减小车体振动新方法; 采用H2与H∞准则优化了压电作动器与压电传感器布置位置, 设计了鲁棒最优控制器, 仿真分析了该方法对车体振动减振的有效性, 为车辆结构减振设计提供参考。
1. 车辆减振力学模型
为分析减振装置对车辆振动的效果, 建立如图 1所示车辆垂向减振力学模型。在传统车辆垂向模型的基础上, 在二系垂向悬挂位置处安装电液作动器, 在车体底架侧梁位置处安装压电作动器。将车体考虑为弹性欧拉梁, 其坐标系原点O位于车体左端, 将构架与轮对考虑为刚体, 假设轮对与钢轨刚性紧密接触, 轨道不平顺即为轮对位移。图 1中: v为列车运行速度; L为车体长度; Ls为转向架定距之半; mc为车体质量; Ic为车体点头转动惯量; mb为构架质量; Ib为构架点头转动惯量; c1、c2分别为一系、二系垂向阻尼; k1、k2分别为一系、二系垂向刚度; U1、U2分别为右侧、左侧二系垂向作动器控制力; b为转向架轴距之半; z (x, t) 为车体垂向振动位移, 包含刚体位移和弹性体位移; x为车体纵向位置坐标; t为车辆运行时间; θc为车体点头位移; zc为车体浮沉位移; zb1、zb2分别为右位、左位构架浮沉位移; θb1、θb2分别为右位、左位构架点头位移; zw1~zw4分别为第1~4轮对垂向位移。根据梁的振动理论并考虑结构阻尼的影响, 可得[20]
式中: E为车体弹性模量; I为车体截面惯性矩; ρ为车体密度; A为车体截面面积; φ为车体内滞阻尼系数; xi为二系悬挂在车体中的纵向位置坐标, i=1对应图 1右位转向架, i=2对应左位转向架; Fi为二系悬挂作用在弹性车体上的力; δ (·) 为Delta函数; n为压电作动器的个数; xl1、xl2分别为第l个压电作动器两固定端的坐标; Ml (x, t) 为第l个压电作动器作用于车体上的弯矩, 其值与输入电压成正比[21]; R为压电作动器弯矩系数; Vl为施加在第l个作动器上的电压; H (·) 为Heaviside函数; d为压电应变系数; g为压电作动器的宽度; Ep为压电作动器弹性模量; zp为压电作动器至车体中性轴的高度。
根据牛顿运动定律, 有
式中: Ui为二系垂向作动器i输出的控制力。
由于车体视为弹性等截面均质欧拉梁, 则其浮沉运动振型函数为Y1 (x) =1, 点头运动振型函数为Y2 (x) =x-L/2。由于车体二系悬挂的刚度和阻尼较小, 故可视为两端自由的欧拉梁, 其弹性振动的第r阶振型函数为
式中: βr为与车体结构参数与频率有关的弧度。
设参数qr (t) 为车体第r阶弹性模态坐标, 应用模态叠加原理, 车体的振动位移为各模态位移的叠加, 取车体前N阶模态有
将式(5) 带入式(1), 沿车体全长积分, 并利用模态的正交性和δ函数的性质, 可得车体及转向架振动方程组为
式中: ξr为车体弹性振型阻尼比; ωr为车体弹性振动频率。
设位移向量为
则系统振动微分方程可写为
式中: M、K、C分别为车辆系统惯量、刚度与阻尼矩阵; F为压电作动器输出力向量; D1为二系垂向作动器系数矩阵; D2为轨道不平顺输入矩阵; Z1为轨道不平顺激扰向量, 各个矩阵都有其相应维数。
令状态向量X为
式(9) 可写为
2. 作动器与传感器位置布置
由于车体二系悬挂空间限制, 对二系垂向可调阻尼减振器的选择限制较大。Foo等的研究表明: 二系垂向可调阻尼减振器可采用电液伺服作动器, 其作动力与频率响应均可满足要求[9]。压电作动器与传感器安装位置对车体减振效果影响很大, 如果安装在弹性振动节点处, 则不会产生作用力及传感信号, 为此可采用H2与H∞准则来优化压电元件布置位置[21]。为实现压电作动器的同位控制, 防止由于模态截断而导致的溢出问题, 在同一部位两侧分别布置压电作动器和压电传感器。由于车体尺寸及所需减振力均较大, 压电作动器采用压电堆栈工作方式, 满足车体弹性振动控制的要求。
对于图 1车辆控制系统, 以压电作动器控制电压为输入, 车体垂向振动位移为输出, 系统传递函数G(s) 的H2与H∞范数分别为
式中: s为复变量; ω为s的虚部; G* (jω) 为G (jω) 的复共轭; σmax[G (jω) ]为G (jω) 的最大奇异值。
H2范数表示系统G (s) 的脉冲响应能量, 使其最小即为系统振动能量最小。
表 1 动车组参数Table 1. Parameters of EMU
采用表 1动车组参数, 取车体前两阶弹性模态, 其量纲为1的H2与H∞范数分别见图 2、3, 可知: 在车体位置坐标x分别为7.15、12.25、17.35m处车体一阶与二阶弹性模态量纲为1的H2及H∞范数最大, 可以作为压电作动器与传感器的布置位置, 见图 4。
3. 车体振动减振控制方法
为了实现车体振动加速度控制, 满足系统的鲁棒性控制要求, 可采用H∞最优控制来实现[22, 23, 24]。H∞控制的基本思想是: 当系统干扰至误差传递函数的H∞范数最小时, 干扰对系统误差的影响最小, 因此, 可采用H∞范数作为目标函数的度量进行优化设计。
车体考虑刚体模态与前两阶弹性模态, 构架和轮对视为刚体, 压电作动器依照图 4布置, 系统的状态空间实现可表示为
式中: w为外部干扰及激扰向量; u为作动器控制输入向量; Z2为被控变量向量, 包括车体垂向加速度、二系垂向作动器控制力及压电作动器控制电压; Y为测量输出向量, 包括车体垂向振动加速度及车体二系悬挂挠度; B4为干扰输入矩阵; B5为控制输入矩阵; C1为性能输出矩阵; C2为测量输出矩阵; D11、D12、D21、D22分别为广义对象的馈通矩阵; V1、V2、V3分别对应图 4中车体位置坐标为7.15、12.25、17.35m处压电作动器控制电压。
测量输出定义为
由式(13) 可知: 输出为车体的浮沉运动加速度、点头运动加速度与车辆二系悬挂动挠度, 依据各向量定义即可得到各系数矩阵。
图 5为系统H∞控制框图, 主要目标是降低车体垂向振动, 提高乘坐舒适性, 同时减小控制器的频率响应范围。
图 5中: K (s) 为镇定控制器传递函数; P为广义对象; WQ为测量噪声Q的权函数, 取0.023;Wf为外界扰动f的权函数, 取0.003 6;WY为测量输出Y的权函数; Wu为控制输入u的权函数, 分别为
式中: W1为振动加速度; W2为二系动挠度; W3为二系垂向作动器; W4为压电作动器权函数。
4. 仿真结果分析
采用表 1高速列车参数与表 2压电作动器参数, 在MATLAB环境中, 利用鲁棒控制工具箱进行编程, 按照前述方法设计H∞范数约束的状态估计最优控制器, 其主要步骤如下。
步骤1:建立式(12) 的数学模型, 明确被控变量、测量变量与干扰输入。
步骤2:根据设计要求, 选择测量噪声、扰动输入、测量输出与控制力加权函数。
表 2 压电作动器参数Table 2. Parameters of piezoelectric actuators
步骤3:设计采用H∞控制的反馈控制规律。
步骤4:通过仿真手段对所设计的系统进行性能评价, 评价指标采用振动加速度功率谱密度与加速度均方根。如系统满足设计要求则结束, 如不满足返回步骤1重新设计。
为分析车体垂向振动减振效果, 有必要首先分析车体自振频率及振型, 根据文献[25]~[27]方法, 依据表 1车辆参数, 自振频率与振型见表 3。
表 3 车辆模态分析结果Table 3. Analysis result of vehicle modes
依据上述步骤, 通过MATLAB仿真得到的车体中部与转向架上方振动加速度功率谱分别见图 6、7, 可知: 在二系垂向作动器和车体压电作动器联合作用下, 车体中部与转向架上方18 Hz以下振动加速度功率谱显著减小; 在一阶垂弯振动频率处, 车体中部加速度功率谱减小为被动悬挂的5%, 转向架上方加速度功率谱减小为被动悬挂的10%;车体中部振动加速度功率谱在大于18 Hz时增大, 由于平稳性指标在该频段以上加权值较小, 而且本身增幅也不大, 不影响减振效果; 在车体浮沉与点头振动频段处, 二系垂向作动器和二系垂向作动器与压电作动器联合作用的效果差别不大, 但在一阶垂弯频率处, 采用联合控制的减振效果比仅采用二系垂向作动器更明显, 可显著减小一阶垂弯处车体的弹性振动, 表明压电作动器对车体一阶垂向弹性振动抑制作用明显。
图 8为采用H∞最优控制器的联合控制车辆与被动悬挂车辆在不同运行速度下的车体中部振动加速度均方根对比, 可以看出: 联合控制车辆振动加速度均方根较被动悬挂小, 速度越大, 减小值越大, 200km·h-1时振动加速度均方根减小0.004m·s-2, 减小了10%, 350km·h-1时振动加速度均方根减小0.018m·s-2, 减小了18%。
图 9为二系垂向作动器控制力功率谱曲线, 可以看出: 在车体浮沉与点头振动频率处二系垂向作动器控制力的功率谱量级为106 N2·Hz-1, 表明在该频段处二系垂向作动器控制力较大, 对车体刚性振动会产生较大抑制作用; 在车体二阶垂弯频率处控制力功率谱量级为103 N2·Hz-1, 表明在该阶频率处二系垂向作动器控制力较小, 对车体振动抑制作用较小。
图 9 二系垂向作动器控制力功率谱Figure 9. Control force power spectrums of secondary vertical actuators图 10为压电作动器输出电压功率谱, 可以看出: 在0~15Hz频段处, 压电作动器输出电压功率谱较大, 特别是在车体一阶垂弯振动频率处, 其电压功率谱达到峰值4 000V2·Hz-1, 表明在压电作动器作用下, 车体一阶垂弯弹性振动得到有效控制; 在约3Hz处, 左、右侧压电作动器较中间压电作动器电压功率谱大25%, 表明在该频率处转向架上方压电作动器需输出更大的作动力, 以控制车体振动。
图 10 压电作动器输出电压功率谱Figure 10. Output voltage power spectrums of piezoelectric actuators5. 结语
(1) 根据减振原理, 提出在车体二系悬挂位置处安装电液作动器、在车体底架侧梁安装压电作动器的动车组车辆减振方法, 建立了安装减振装置的车辆系统力学模型, 设计了主动悬挂H∞最优控制器, 分析结果表明, 该方法能显著降低车体刚性与弹性振动, 尤其是车体一阶垂弯振动, 速度越高, 减振效果越明显。
(2) 压电作动器与传感器位置布置可采用归一化H2/H∞范数来优化, 为避免模态截断带来的溢出问题, 压电作动器与传感器应采用同位控制。
(3) 仿真结果表明, 采用H∞鲁棒最优控制时, 压电作动器的控制电压和电液作动器的输出力均能满足控制要求, 抑制车体振动, 改善运行平稳性, 但由于控制仿真计算的局限性, 下一步应通过比例实验台与实车试验进行验证。
-
图 9 二系垂向作动器控制力功率谱
Figure 9. Control force power spectrums of secondary vertical actuators
图 10 压电作动器输出电压功率谱
Figure 10. Output voltage power spectrums of piezoelectric actuators
-
[1] SHI Huai-long, WU Ping-bo. Flexible vibration analysis for car body of high-speed EMU[J]. Journal of Mechanical Science and Technology, 2016, 30 (1): 55-66. doi: 10.1007/s12206-015-1207-6 [2] LING Liang, ZHANG Qing, XIAO Xin-biao, et al. Integration of car-body flexibility into train-track coupling system dynamics analysis[J]. Vehicle System Dynamics, 2018, 56 (4): 485-505. doi: 10.1080/00423114.2017.1391397 [3] DUMITRIU M. A new passive approach to reducing the carbody vertical bending vibration of railway vehicles[J]. Vehicle System Dynamics, 2017, 55 (11): 1787-1806. doi: 10.1080/00423114.2017.1330962 [4] GONG Dao, ZHOU Jin-song, SUN Wen-jing. Influence of under-chassis-suspended equipment on high-speed EMU trains and the design of suspension parameters[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016, 230 (8): 1790-1802. doi: 10.1177/0954409715614601 [5] 黄彩虹, 曾京. 基于约束阻尼层的高速客车车体弯曲振动的抑制[J]. 交通运输工程学报, 2010, 10 (1): 36-42. doi: 10.3969/j.issn.1671-1637.2010.01.007HUANG Cai-hong, ZENG Jing. Flexural vibration suppression of car body for high-speed passenger car based on constrained damping layers[J]. Journal of Traffic and Transportation Engineering, 2010, 10 (1): 36-42. (in Chinese). doi: 10.3969/j.issn.1671-1637.2010.01.007 [6] SUZUKI Y, MAEBASHI E, AKUTSU K, et al. Method for flexural vibration damping of rolling stock carbody[J]. Quarterly Report of Railway Technical Research Institute, 1997, 38 (3): 123-128. [7] SCHANDL G, LUGNER P, BENATZKY C, et al. Comfort enhancement by an active vibration reduction system for a flexible railway car body[J]. Vehicle System Dynamics, 2007, 45 (9): 835-847. doi: 10.1080/00423110601145952 [8] KOZEK M, BENATZKY C, SCHIRRER A, et al. Vibration damping of a flexible car body structure using piezo-stack actuators[J]. Control Engineering Practice, 2011, 19 (3): 298-310. doi: 10.1016/j.conengprac.2009.08.001 [9] FOO E, GOODALL R M. Active suspension control of flexiblebodied railway vehicles using electro-hydraulic and electromagnetic actuators[J]. Control Engineering Practice, 2000, 8 (5): 507-518. doi: 10.1016/S0967-0661(99)00188-4 [10] SUGAHARA Y, KAZATO A, KOGANEI R, et al. Suppression of vertical bending and rigid-body-mode vibration in railway vehicle car body by primary and secondary suspension control: results of simulations and running tests using Shinkansen vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223 (6): 517-531. doi: 10.1243/09544097JRRT265 [11] SUGAHARA Y, KAZATO A, TAKIGAMI T, et al. Suppression of vertical vibration in railway vehicles by controlling the damping force of primary and secondary suspensions[J]. Quarterly Report of Railway Technical Research Institute, 2008, 49 (1): 7-15. [12] SUZUKI Y, AKUTSU K. Theoretical analysis of flexural vibration of car body[J]. Quarterly Report of Railway Technical Research Institute, 1990, 31 (1): 42-48. [13] DIANA G, CHELI F, COLLINA A, et al. The development of a numerical model for railway vehicles comfort assessment through comparison with experimental measurements[J]. Vehicle System Dynamics, 2002, 38 (3): 165-183. doi: 10.1076/vesd.38.3.165.8287 [14] 曹辉, 张卫华, 缪炳荣. 车体弹性效应下的垂向振动特性研究[J]. 铁道学报, 2017, 39 (6): 48-54. doi: 10.3969/j.issn.1001-8360.2017.06.006CAO Hui, ZHANG Wei-hua, MIAO Bing-rong. Research on vertical vibration characteristic of car body under flexible effect[J]. Journal of the China Railway Society, 2017, 39 (6): 48-54. (in Chinese). doi: 10.3969/j.issn.1001-8360.2017.06.006 [15] KAMADA T, KIUCHI R, NAGAI M. Suppression of railway vehicle vibration by shunt damping using stack type piezoelectric transducers[J]. Vehicle System Dynamics, 2008, 46 (S): 561-570. [16] TAKIGAMI T, TOMIOKA T. Investigation to suppress bending vibration of railway vehicle carbodies using piezoelectric elements[J]. Quarterly Report of Railway Technical Research Institute, 2005, 46 (4): 225-230. [17] MOHEIMANI S O R. A survey of recent innovations in vibration damping and control using shunted piezoelectric transducers[J]. IEEE Transactions on Control Systems Technology, 2003, 11 (4): 482-494. doi: 10.1109/TCST.2003.813371 [18] TAKIGAMI T, TOMIOKA T, HANSSON J. Vibration suppression of railway vehicle carbody with piezoelectric elements (a study by using a scale model of Shinkansen)[J]. Japan Society of Mechanical Engineers, 2005, 71 (4): 1254-1262. [19] MOLATEFI H, AYOUBI P, MOZAFARI H. Active vibration control of a railway vehicle carbody using piezoelectric elements[J]. Chinese Journal of Mechanical Engineering, 2017, 30 (4): 363-972. [20] HALIM D, MOHEIMANI S O R. Spatial resonant control of flexible structures—application to a piezoelectric laminate beam[J]. IEEE Transactions on Control Systems Technology, 2001, 9 (1): 37-53. doi: 10.1109/87.896744 [21] HALIM D, MOHEIMANI S O R. Spatial H2control of a piezoelectric laminate beam: experimental implementation[J]. IEEE Transactions on Control Systems Technology, 2002, 10 (4): 533-546. doi: 10.1109/TCST.2002.1014673 [22] KAMADA T, HIRAIZUMI K, NAGAI M. Active vibration suppression of lightweight railway vehicle body by combined use of piezoelectric actuators and linear actuators[J]. Vehicle System Dynamics, 2010, 48 (S): 73-87. [23] ORVNS A, STICHEL S, PERSSON R. Active lateral secondary suspension with H∞control to improve ride comfort: simulations on a full-scale model[J]. Vehicle System Dynamics, 2011, 49 (9): 1409-1422. doi: 10.1080/00423114.2010.527011 [24] MOUSAVI BIDELEH S M, MEI T X, BERBYUK V. Robust control and actuator dynamics compensation for railway vehicles[J]. Vehicle System Dynamics, 2016, 54 (12): 1762-1784. doi: 10.1080/00423114.2016.1234627 [25] 曾京, 邬平波, 郝建华. 铁道客车系统的垂向减振分析[J]. 中国铁道科学, 2006, 27 (3): 62-67. doi: 10.3321/j.issn:1001-4632.2006.03.011ZENG Jing, WU Ping-bo, HAO jian-hua. Analysis of vertical vibration reduction for railway vehicle systems[J]. China Railway Science, 2006, 27 (3): 62-67. (in Chinese). doi: 10.3321/j.issn:1001-4632.2006.03.011 [26] 黄彩虹, 曾京, 邬平波, 等. 铁道客车车体弹性振动减振研究[J]. 工程力学, 2010, 27 (12): 250-256. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201012041.htmHUANG Cai-hong, ZENG Jing, WU Ping-bo, et al. Study on car body flexible vibration reduction for railway passenger carriage[J]. Engineering Mechanics, 2010, 27 (12): 250-256. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201012041.htm [27] 曾京, 罗仁. 考虑车体弹性效应的铁道客车系统振动分析[J]. 铁道学报, 2007, 29 (6): 19-25. doi: 10.3321/j.issn:1001-8360.2007.06.004ZENG Jing, LUO Ren. Vibration analysis of railway passenger car systems by considering flexible carbody effect[J]. Journal of the China Railway Society, 2007, 29 (6): 19-25. (in Chinese). doi: 10.3321/j.issn:1001-8360.2007.06.004 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 666
- HTML全文浏览量: 186
- PDF下载量: 316
- 被引次数: 0
