A dynamic evolution model of disequilibrium network traffic flow with quantity regulation of congestion
-
摘要: 基于经济学非瓦尔拉斯均衡理论, 采用经济学中市场摸索过程模拟出行者路径选择行为; 假设城市出行者在路径决策过程中, 考虑路径出行时间和关键路径拥挤程度的共同影响, 以价格拥挤混合均衡交通流模式为基础, 建立了一种价格-拥挤混合调节的非均衡网络交通流动态演化模型, 并验证了模型稳定状态与均衡的等价性; 基于简单的测试网络和中型路网, 对演化模型进行了模拟, 描述了非均衡网络交通流的演化过程与非均衡状态下交通网络的整体表现。研究结果表明: 时间价格调节模型的演化结果符合经典的Wardrop第一原理, 拥挤数量调节的结果使得OD间各路径上关键路段的拥挤程度一致, 价格-拥挤混合调节的结果会使路径流在走行费用较小和拥挤程度较低的路径上相互进行调整, 其动态演化过程波动性要大于单一调节的情况; 在测试路网中, 考虑采用拥挤程度对路径进行选择的行为, 使得整个路网拥挤均匀程度整体提高62%, 但路段饱和度均值却从0.60增大到了0.64, 表明路网整体上变得拥挤; 若考虑两者的共同调节, 最拥堵路段饱和度从0.936下降到0.787, 均匀程度整体提高46%, 且路段饱和度均值降低, 路径行程时间变小, 拥堵得到改善; 中型路网的测试结果也表明这种混合均衡模式能灵活、客观地描述路网交通流动态演化过程, 获得较为合理的路网系统的稳态流量。Abstract: Supposing that the travel cost on the paths and the congestion degree on the key links were considered by the urban travelers, aprice-congestion mixed dynamic evolution model was established based on analyzing the equilibrium flow model.The model was based on the economics theory of non-Walrasian equilibrium method and by simulating the traveler's route choice behavior following the economical concept of market exploration process, the equivalency of model stability and equalization was verified.The evolution model was simulated by using a simple test network and a medium size network, the evolution process of disequilibrium network traffic flow and the performance of traffic network under the disequilibrium situation were described.Analysis result indicates that the evolution model of time price regulation accords with the classical Wardrop's first principle; the result of quantity regulation of congestion allows the degree of congestion on the key links of each path between OD to be the same; the result of pricecongestion mixed regulation allows the path flow to be adjusted between the paths of lower cost and the ones of less congestion, the undulation of dynamic evolution of which is greater than that of the single regulation.In the test network, because the model only considers the choice behavior of congestion degree upon path, the congestion degree of whole traffic network is more uniform, and compared with the single price regulation model, the overall uniformity coefficient improves by 62%.However, the mean link saturation improves from 0.60 to 0.64, which indicates that the traffic network becomes congested overall.By considering the joint regulation of these two factors, the saturation of most congested link decreases from 0.936 to 0.787.The overall uniformity coefficient improves by 46%.The mean saturation of links, path travel time and congestion decrease.The test result of the medium size network also shows that such mixed equilibrium model can describe the dynamic evolution process of traffic flow on traffic network flexibly and objectively, and achieve steady state flow of traffic network system, which canexplain the traffic travel behavior better.8 tabs, 9 figs, 32 refs.
-
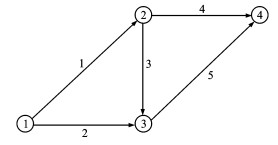
Figure 1. Test traffic network[10]
Table 1. Cost function parameters

Table 2. Evolution model parameters

Table 3. Fixed demand equilibrium network path flow, cost and maximum congestion degree

Table 4. Fixed demand equilibrium network path flow and maximum congestion degree

Table 5. Fixed demand equilibrium network path flow, cost and maximum congestion degree

Table 6. Calculated values of saturation of road link under different regulation mechanisms

Table 7. Parameters of each link cost function

Table 8. Fixed demand equilibrium network path flow, cost and maximum congestion degree

-
[1] BOYCE D. Beckmann's transportation network equilibrium model: Its history and relationship to the Kuhn-Tucker conditions[J]. Economics of Transportation, 2013, 2 (1): 47-52. doi: 10.1016/j.ecotra.2012.11.002 [2] XU Hong-li. Urban transportation network equilibrium andcongestion pricing with bounded rationality[D]. Nanjing: Nanjing University, 2011. [3] KUMAR A, PEETA S. A day-to-day dynamical model for the evolution of path flows under disequilibrium of traffic networks with fixed demand[J]. Transportation Research Part B: Methodological, 2015, 80: 235-256. doi: 10.1016/j.trb.2015.07.014 [4] HE Xiao-zheng, PEETA S. Amarginal utility day-to-day traffic evolution model based on one-step strategic thinking[J]. Transportation Research Part B: Methodological, 2016, 84: 237-255. doi: 10.1016/j.trb.2015.12.003 [5] SMITH M J. The existence and calculation of traffic equilibria[J]. Transportation Research Part B: Methodological, 1983, 17 (4): 291-303. doi: 10.1016/0191-2615(83)90047-4 [6] SMITH M J. The stability of a dynamic model of traffic assignment-an application of a method of Lyapunov[J]. Transportation Science, 1984, 18 (3): 245-252. doi: 10.1287/trsc.18.3.245 [7] SMITH M J, WINSTERN M B. A continuous day-to-day traffic assignment model and the existence of a continuous dynamic user equilibrium[J]. Annals of Operations Research, 1995, 60 (1): 59-79. doi: 10.1007/BF02031940 [8] HUANG Hai-jun, LAM W. Modeling and solving the dynamic user equilibrium route and departure time choice problem in network with queues[J]. Transportation Research Part B: Methodological, 2002, 36 (3): 253-273. doi: 10.1016/S0191-2615(00)00049-7 [9] PEETA S, YANG T H. Stability issues for dynamic traffic assignment[J]. Automatica, 2003, 39 (1): 21-34. doi: 10.1016/S0005-1098(02)00179-6 [10] FRIESZT L. Day-to-day dynamic network disequilibria and idealized traveler information systems[D]. Fairfax: George Mason University, 1994. [11] ZHANG Ding, NAGURNEY A. On the local and global stability of a travel route choice adjustment process[J]. Transportation Research Part B: Methodological, 1996, 30 (4): 245-262. doi: 10.1016/0191-2615(95)00034-8 [12] ZHANG Ding, NAGURNEY A. On the equivalence between stationary link flow patterns and traffic network equilibria[J]. Transportation Research Part B: Methodological, 2001, 35 (8): 731-748. doi: 10.1016/S0191-2615(00)00020-5 [13] SANDHOLM W H. Potential games with continuous player sets[J]. Journal of Economic Theory, 2001, 97 (1): 81-108. doi: 10.1006/jeth.2000.2696 [14] YANG F. An evolutionary game theory approach to the dayto-day traffic dynamics[D]. Madison: University of WisconsinMadison, 2005. [15] YANG Fan, ZHANG Ding. Day-to-day stationary link flow pattern[J]. Transportation Research Part B: Methodological, 2009, 43 (1): 119-126. doi: 10.1016/j.trb.2008.05.005 [16] TARUN R, BOYLES S D. Dynamic pricing in discrete time stochastic day-to-day route choice models[J]. Transportation Research Part B: Methodological, 2016, 92: 104-118. doi: 10.1016/j.trb.2016.01.008 [17] GUO Ren-yong, YANG Hai, HUANG Hai-jun. Day-to-day flow dynamics and congestion control[J]. Transportation Science, 2016, 50 (3): 982-997. doi: 10.1287/trsc.2015.0596 [18] BROWN D B, GIORGI E D, SIM M. Aspirational preferencesand their representation by risk measures[J]. Management Science, 2012, 58 (11): 2095-2113. doi: 10.1287/mnsc.1120.1537 [19] TAN Zhi-jia, YANG Hai, GUO Ren-yong. Dynamic congestion pricing with day-to-day flow evolution and user heterogeneity[J]. Transportation Research Part C: Emerging Technologies, 2015, 61: 87-105. doi: 10.1016/j.trc.2015.10.013 [20] XIAO Feng, YANG Hai, YE Hong-bo. Physics of day-today network flow dynamics[J]. Transportation Research Part B: Methodological, 2016, 86: 86-103. doi: 10.1016/j.trb.2016.01.016 [21] HAN Lan-shan, DU Li-li. On a link-based day-to-day traffic assignment model[J]. Transportation Research Part B: Methodological, 2012, 46 (1): 72-84. doi: 10.1016/j.trb.2011.09.005 [22] WU Jian-jun, SUN Hui-jun, WANG D Z W, et al. Boundedrationality based day-to-day evolution model for travel behavior analysis of urban railway network[J]. Transportation Research Part C: Emerging Technologies, 2013, 31: 73-82. doi: 10.1016/j.trc.2013.01.010 [23] IRYO T. Day-to-day dynamical model incorporating an explicit description of individuals'information collection behaviour[J]. Transportation Research Part B: Methodological, 2016, 92: 88-103. doi: 10.1016/j.trb.2016.01.009 [24] CAREY M. The dual of the traffic assignment problem with elastic demands[J]. Transportation Research Part B: Methodological, 1985, 19 (3): 227-237. doi: 10.1016/0191-2615(85)90006-2 [25] CAREY M. Network equilibrium: optimization formulations with both quantities and prices as variable[J]. Transportation Research Part B: Methodological, 1987, 21 (1): 69-77. doi: 10.1016/0191-2615(87)90022-1 [26] HUANG Zhong-xiang, HE Guo-guang, LIU Bao. Disequilbrium traffic assignment models by price-quantity regulation[J]. Journal of System Engineering, 1999, 14 (2): 145-151. [27] HUANG Zhong-xiang, HE Guo-guang, LIU Bao. A primary study on disequilibrium transportation planning[J]. Journal of Management Sciences in China, 2001, 4 (1): 52-57. [28] ZHANG Jun-yi, MONDEN H. Transport demand and supply model based on disequilibrium theory[J]. Journal of the Eastern Asia Society for Transportation Studies, 2003 (5): 1262-1277. [29] GUO Ren-yong, HUANG Hai-jun. Dynamical evolutionary model of traffic assignment under AITS[J]. Journal of Management Sciences in China, 2008, 11 (2): 12-19. [30] HUANG Zhong-xiang, CAI Jian-rong, WU Li-xuan. Disequilibrium adjustment mechanism for urban resident travel markets[J]. Journal of Chang'an University: Natural Science Edition, 2016, 36 (6): 105-110. [31] FRIESZ T L, SUO Zhong-gui, BERNSTEIN D. A dynamic disequilibrium interregional commodity flow model[J]. Transportation Research Part B: Methodological, 1998, 32 (7): 467-483. doi: 10.1016/S0191-2615(98)00012-5 [32] NGUYEN S, DUPIU C. An efficient method for computing traffic equilibria in networks with asymmetric transportation costs[J]. Transportation Science, 1984, 18 (2): 185-202. doi: 10.1287/trsc.18.2.185 -





 下载:
下载: