An ant colony optimization algorithm of stochastic user equilibrium traffic assignment problem
-
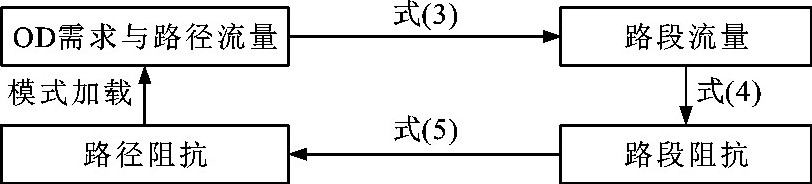
摘要: 研究了出行者对路网熟悉程度的指标与交通流分配均衡性之间的关系, 提出了具有指数形式信息素更新策略的随机用户均衡模型蚁群优化算法, 建立了从Logit模型加载, 到交通需求确认及路径流量、路段流量、路段阻抗、路径阻抗迭代计算的交通分配动态循环流程; 计算了Nguyen-Dupuis路网模型中各路段的流量与阻抗, 并与连续平均算法计算结果进行比较; 通过调节出行者对路网熟悉程度的因子, 分析了蚁群优化算法与连续平均算法的敏感性。研究结果表明: 采用连续平均算法和蚁群优化算法计算的路段流量分布分别为20~280、40~260pcu, 蚁群优化算法的流量分布区间减小了15.4%, 路段流量的最大值减小了7.1%, 因此, 采用蚁群优化算法计算的路段流量较为均衡; 采用蚁群优化算法时, 在Nguyen-Dupuis路网模型中各路段流量的标准差从65pcu降至48pcu, 88%可选路径的阻抗分布在61~64, 且84%的路径阻抗低于采用连续平均算法计算的阻抗, 因此, 采用蚁群优化算法减少了用户出行时间; 当路网熟悉程度分别为0.01、0.1、1、2、7、11时, 采用连续平均算法计算的路段流量标准差分别为75、65、50、47、45、45pcu, 采用蚁群优化算法计算的路段流量标准差分别为48、48、48、47、43、43pcu, 可见, 随着路网熟悉程度的增大, 分配在各路段上的流量范围逐渐减小, 标准差趋于稳定, 信息素更新策略对出行者的路径选择概率影响越明显, 出行者选择阻抗小的路径的概率变大, 因此, 采用蚁群优化算法对路段的流量分配逐渐优于连续平均算法。Abstract: The relationship between the indicators of the traveler's familiarity with the road network and the equilibrium of traffic flow assignment was studied. An ant colony optimization algorithm with the pheromone update strategy of exponential form was proposed to solve the stochastic user equilibrium problem. In addition, the dynamic cycle process of traffic assignment was established from the logit model loading to the iterative calculations of traffic demand, path flow, road flow, road impedance and path impedance. The road flows and road impedances of Nguyen-Dupuis road network model were calculated and compared with the result computed by the successive average algorithm. The sensitivities of ant colony optimization algorithm and successive average algorithm were analyzed by adjusting the factors of the traveler's familiaritywith the road network. Analysis result shows that the road flow distributions computed by the successive average algorithm and ant colony optimization algorithm are 20-280 and 40-260 pcu, respectively, and the flow distribution interval computed by the latter decreases by 15.4%, while the maximum road flow decreases by 7.1%. Therefore, the road flow calculated by the ant colony optimization algorithm is more balanced. When using the ant colony optimization algorithm, the standard deviation of each road section flow in Nguyen-Dupuis road network model reduces from 65 to 48 pcu, 88% of the alternative paths' impedances distribute in 61-64, and 84% of the path impedances are lower than the result computed by the successive average algorithm. Therefore, the ant colony optimization algorithm can reduce the user travel time. When the familiarity of the road network is 0.01, 0.1, 1, 2, 7, and 11, respectively, the standard deviation of each road section calculated by the successive average algorithm is 75, 65, 50, 47, 45, and 45 pcu, respectively, and the standard deviation calculated by the ant colony optimization algorithm is 48, 48, 48, 47, 43, and 43 pcu, respectively. With the increase of road network familiarity, the range of the flow assigned to each road gradually decreases, and the standard deviation tends to be stable. The pheromone update strategy has greater influence on the probability of traveler's path selection, and the probability selecting the path with smaller impedance is higher. Therefore, the ant colony optimization algorithm gradually outperforms the successive average algorithm for the flow distribution of each road section.
-
表 1 路段的基本属性
Table 1. Basic properties of roads

表 2 路网中的有效路径
Table 2. Effective paths in road network

-
[1] FRIESZ T L, BERNSTEIN D, SUO Z, et al. Dynamic network user equilibrium with state-dependent time lags[J]. Networks and Spatial Economics, 2001, 1: 319-347. doi: 10.1023/A:1012896228490 [2] HUANG Hai-jun, LAM W H K. Modeling and solving the dynamic user equilibrium route and departure time choice problem in network with queues[J]. Transportation Research Part B: Methodological, 2002, 36 (3): 253-273. doi: 10.1016/S0191-2615(00)00049-7 [3] CHOW A H F. Dynamic system optimal traffic assignment—a state-dependent control theoretic approach[J]. Transportmetrica, 2009, 5 (2): 85-106. doi: 10.1080/18128600902717483 [4] ZHONG R X, SUMALEE A, FRIESZ T L, et al. Dynamic user equilibrium with side constraints for a traffic network: theoretical development and numerical solution algorithm[J]. Transportation Research Part B: Methodological, 2011, 45 (7): 1035-1061. doi: 10.1016/j.trb.2011.05.004 [5] DAGANZO C F, SHEFFI Y. On stochastic models of traffic assignment[J]. Transportation Science, 1977, 11 (3): 253-274. doi: 10.1287/trsc.11.3.253 [6] LIU Hao-xiang, WANG D Z W. Global optimization method for network design problem with stochastic user equilibrium[J]. Transportation Research Part B: Methodological, 2015, 72: 20-39. doi: 10.1016/j.trb.2014.10.009 [7] CHEN A, RYU S, XU Xiang-dong, et al. Computation and application of the paired combinatorial logit stochastic user equilibrium problem[J]. Computers and Operations Research, 2014, 43: 68-77. doi: 10.1016/j.cor.2013.08.022 [8] RASMUSSEN T K, WATLING D P, PRATO C G, et al. Stochastic user equilibrium with equilibrated choice sets: PartⅡ—solving the restricted SUE for the logit family[J]. Transportation Research Part B: Methodological, 2015, 77: 146-165. doi: 10.1016/j.trb.2015.03.009 [9] MAHER M. Stochastic user equilibrium assignment with elastic demand[J]. Traffic Engineering and Control, 2001, 42 (5): 163-167. [10] KUANG A W, HUANG Z X. Stochastic user equilibrium traffic assignment with multiple user classes and elastic demand[C]∥IEEE. 2010International Conference on Intelligent Computation Technology and Automation. New York: IEEE, 2010: 394-397. [11] MENG Qiang, LAM W H K, YANG Liu. General stochastic user equilibrium traffic assignment problem with link capacity constraints[J]. Journal of Advanced Transportation, 2008, 42 (4): 429-465. doi: 10.1002/atr.5670420403 [12] KUANG A W, HUANG Z X. A research on mixed stochastic user equilibrium model based on generalized travel disutility under ATIS[C]∥IEEE. 2010International Conference on Intelligent Computation Technology and Automation. New York: IEEE, 2010: 324-327. [13] MENG Qiang, LIU Zhi-yuan. Mathematical models and computational algorithms for probit-based asymmetric stochastic user equilibrium problem with elastic demand[J]. Transportmetrica, 2012, 8 (4): 261-290. doi: 10.1080/18128601003736026 [14] 周晶. 随机交通均衡配流模型及其等价的变分不等式问题[J]. 系统科学与数学, 2003, 23 (1): 120-127. doi: 10.3969/j.issn.1000-0577.2003.01.017ZHOU Jing. Stochastic user equilibrium and its variational inequality problem[J]. Journal of Systems Science and Mathematical Sciences, 2003, 23 (1): 120-127. (in Chinese). doi: 10.3969/j.issn.1000-0577.2003.01.017 [15] 况爱武, 王正武, 李炳林. 多用户类弹性需求随机用户均衡模型及其求解[J]. 长沙理工大学学报: 自然科学版, 2007, 4 (2): 16-20. https://www.cnki.com.cn/Article/CJFDTOTAL-HNQG200702002.htmKUANG Ai-wu, WANG Zheng-wu, LI Bing-lin. Model and its solution for stochastic user equilibrium traffic assignment with multiple user classes and variable demand[J]. Journal of Changsha University of Science and Technology: Natural Science, 2007, 4 (2): 16-20. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HNQG200702002.htm [16] 陈群, 王艳, 陈维亚, 等. 一种新的概率型随机用户均衡问题表示方法及算法[J]. 中国公路学报, 2014, 27 (8): 82-88. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201408015.htmCHEN Qun, WANG Yan, CHEN Wei-ya, et al. New expression and algorithm for probit-based stochastic user equilibrium[J]. China Journal of Highway and Transport, 2014, 27 (8): 82-88. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201408015.htm [17] 周博见, 李旭宏, 何杰. 求解基于路径的Logit型随机用户均衡模型的新算法[J]. 中国公路学报, 2014, 27 (3): 100-107. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201403018.htmZHOU Bo-jian, LI Xu-hong, HE Jie. A new algorithm for path-based logit stochastic user equilibrium model[J]. China Journal of Highway and Transport, 2014, 27 (3): 100-107. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201403018.htm [18] 徐兵, 朱道立. 多用户多准则固定需求随机交通均衡变分模型[J]. 公路交通科技, 2007, 24 (4): 129-133. doi: 10.3969/j.issn.1002-0268.2007.04.030XU Bing, ZHU Dao-li. A multiclass and multicriteria stochastic traffic network equilibrium variational inequality model with fixed demand[J]. Journal of Highway and Transportation Research and Development, 2007, 24 (4): 129-133. (in Chinese). doi: 10.3969/j.issn.1002-0268.2007.04.030 [19] DORIGO M, BIRATTARI M, STÜTZLE T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1 (4): 28-39. doi: 10.1109/MCI.2006.329691 [20] LIAO Tian-jun, SOCHA K, MONTES DE OCA M A, et al. Ant colony optimization for mixed-variable optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18 (4): 503-518. [21] MATTEUCCI M, MUSSONE L. Ant colony optimization technique for equilibrium assignment in congested transportation networks[C]∥Association for Computing Machinery. 8th Annual Genetic and Evolutionary Computation Conference. New York: Association for Computing Machinery, 2006: 87-88. [22] D'ACIERNO L, MONTELLA B, DE LUCIA F, et al. A stochastic traffic assignment algorithm based on ant colony optimization[J]. Lecture Notes in Computer Science, 2006, 4150: 25-36. [23] MATTEUCCI M, MUSSONE L. An ant colony system for transportation user equilibrium analysis in congested networks[J]. Swarm Intelligence, 2013, 7 (4): 255-277. [24] 徐勋倩, 黄卫. 蚂蚁算法处理动态交通网络用户均衡配流问题[J]. 公路交通科技, 2005, 22 (1): 111-114. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200501029.htmXU Xun-qian, HUANG Wei. Ant algorithm for users equilibrium assignment model of dynamic traffic network[J]. Journal of Highway and Transportation Research and Development, 2005, 22 (1): 111-114. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200501029.htm [25] 安毅生, 袁绍欣, 赵祥模, 等. 基于蚁群算法的动态路径选择优化方法[J]. 交通运输系统工程与信息, 2014, 14 (3): 97-103. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201403015.htmAN Yi-sheng, YUAN Shao-xin, ZHAO Xiang-mo, et al. Optimization of dynamic route choice based on ant colony algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14 (3): 97-103. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201403015.htm [26] SHEFFI Y, POWELL W B. An algorithm for the equilibrium assignment problem with random link times[J]. Networks, 1982, 12 (2): 191-207. -





 下载:
下载: