Alternate evolution algorithm based on plant growth simulation for berth-quay crane joint allocation model
-
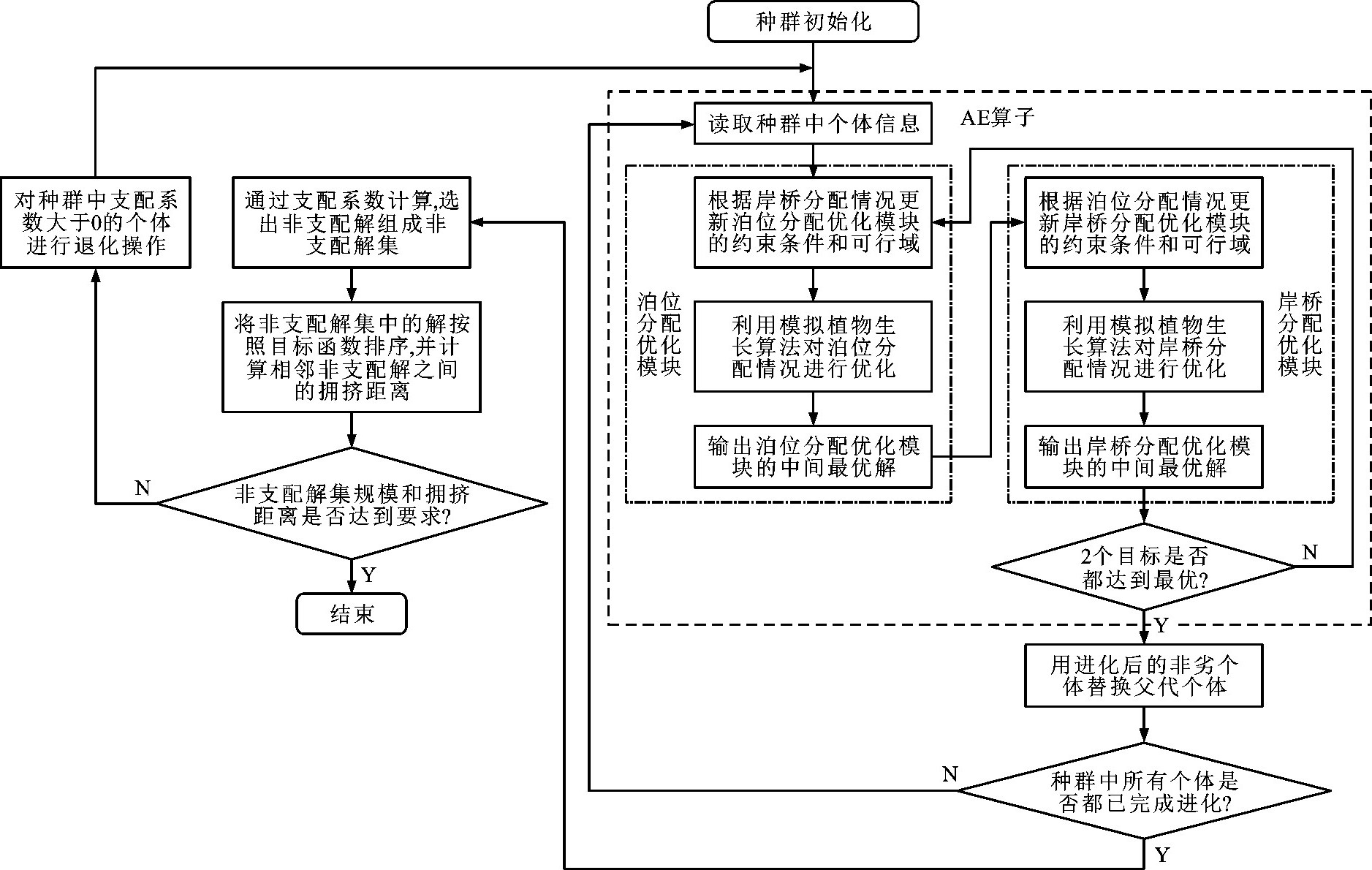
摘要: 为了综合优化集装箱码头泊位和岸桥联合分配计划, 分析了二者的相互独立性和系统关联性; 利用相互独立性, 分别针对泊位和岸桥分配建立了以平均在港时间和作业成本最小为目标的2个优化子模型; 利用系统关联性, 构建了泊位-岸桥联合分配的约束条件, 将2个子模型紧密联系在一起, 建立了完整的泊位-岸桥联合分配模型; 分析了联合分配模型的特点, 设计了模拟植物生长交替进化算法求解模型, 利用基于模拟植物生长算法的交替进化算子对种群中每个个体的2个目标进行交替优化, 进而实现种群进化, 通过算法框架实现非支配解筛选, 经多次种群进化和非支配解筛选, 获得泊位-岸桥联合分配的Pareto满意解集; 针对大连港集装箱码头3d中共计31艘真实到港船舶的泊位-岸桥联合分配计划进行优化计算, 并与多目标遗传算法的计算结果进行对比。计算结果表明: 共获得13个满意解, 船舶平均在港时间为7.47~9.44h, 使用岸桥次数为85~96台, 作业总成本为20.868~21.114万元; 与多目标遗传算法相比, 进化算法的运算速度提高了6.07%, 所得非支配解的数量增加了4个, 增加幅度为30.76%, 且计算结果更趋近于Pareto前沿, 联合分配计划优化程度较高。可见, 采用模拟植物生长交替进化算法能够最大限度地保持种群进化过程中个体的独立性, 获得更多的非劣解, 且交替进化的方式能够使结果更逼近Pareto前沿。Abstract: To optimize the berth-quay crane joint allocation plans in a container terminal synthetically, the independence and system relevance between berth and quay crane were analysed. Based on the independence, two optimized sub-models were established, one to target the berth with the minimum average time in port, and the other to target the quay cranes with the minimum operating cost. Based on the system relevance, the constraint conditions for berth-quay crane joint allocation were constructed, the two sub-models were linked closely, and a complete berth-quay crane joint allocation model was established. The characteristics of the joint allocation model were analysed, and an alternate evolution algorithm based on plant growth simulation wasdesigned to solve it. Alternate evolution operators based on the plant growth simulation algorithm were used to alternately optimize the two targets of each individual in the population to achieve population evolution. The non-dominated solutions were screened through the algorithm framework. After multiple population evolutions and non-dominated solution screening, the Pareto satisfactory solution set for the berth-quay crane joint allocation was obtained. A berthquay crane joint allocation plan for 31 vessels arriving within 3 din the container terminal of Dalian Port was optimized and compared with the multi-objective genetic algorithm. Calculation result shows that 13 satisfactory solutions are obtained. The average vessel time in the port is 7.47-9.44 h, the number of quay cranes used is 85-96 and the total operating cost is 208 680-211 140 yuan. Compared with the optimization results of the multi-objective genetic algorithm, the computation speed is 6.07% faster, and four more non-dominated solutions are achieved with an increase rate of 30.76%, the results are closer to the Pareto frontier and the optimization degree of joint allocation plan is higher. The designed alternate evolution algorithm based on plant growth simulation maintains the maximized independence of an individual in the population evolution process and obtains more non-inferior solutions, and the alternate evolutionary approach provides results closer to the Pareto frontier.
-
表 1 到港船舶数据
Table 1. Data of arriving vessels

表 2 满意解
Table 2. Satisfactory solutions

表 3 两种算法计算结果对比
Table 3. Computation result comparison of two algorithms

-
[1] IMAI A, NISHIMURA E, PAPADIMITRIOU S. The dynamic berth allocation problem for a container port[J]. Transportation Research Part E: Methodological, 2001, 37 (4): 401-417. [2] ZHEN Lu, LIANG Zhe, ZHUGE Dan, et al. Daily berth planning in a tidal port with channel flow control[J]. Transportation Research Part B: Methodological, 2017, 106: 193-217. doi: 10.1016/j.trb.2017.10.008 [3] LEE D H, CHEN Jiang-hang, CAO Jin-xin. The continuous berth allocation problem: agreedy randomized adaptive search solution[J]. Transportation Research Part E: Logistics and Transportation Review, 2010, 46 (6): 1017-1029. doi: 10.1016/j.tre.2010.01.009 [4] TAVAKKOLI-MOGHADDAM R, MAKUI A, SALAHI S, et al. An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports[J]. Computers and Industrial Engineering, 2009, 56 (1): 241-248. doi: 10.1016/j.cie.2008.05.011 [5] 常祎妹, 朱晓宁. 不确定因素下的集装箱码头车船间装卸作业集成调度[J]. 交通运输工程学报, 2017, 17 (6): 115-124. doi: 10.3969/j.issn.1671-1637.2017.06.013CHANG Yi-mei, ZHU Xiao-ning. Integrated scheduling of handling operation between train and vessel in container terminal under uncertain factor[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (6): 115-124. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.06.013 [6] PARK Y M, KIM K H. A scheduling method for berth and quay cranes[J]. OR Spectrum, 2003, 25 (1): 1-23. doi: 10.1007/s00291-002-0109-z [7] 范丽先, 王行苑, 尹静波. 基于公平原则的泊位-岸桥联合调度研究[J]. 工业工程与管理, 2017, 22 (2): 60-68. https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201702010.htmFAN Li-xian, WANG Xing-yuan, YIN Jing-bo. Joint scheduling of berth-quay crane based on fair principle[J]. Industrial Engineering and Management, 2017, 22 (2): 60-68. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201702010.htm [8] LIANG Cheng-ji, HUANG You-fang, YANG Yang. A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning[J]. Computers and Industrial Engineering, 2009, 56 (3): 1021-1028. doi: 10.1016/j.cie.2008.09.024 [9] LI Feng, SHEU J B, GAO Zi-you. Solving the continuous berth allocation and specific quay crane assignment problems with quay crane coverage range[J]. Transportation Science, 2015, 49 (4): 968-989. doi: 10.1287/trsc.2015.0619 [10] 张睿, 靳志宏, 邢曦文, 等. 同贝同步模式下的集装箱装卸作业调度优化[J]. 系统工程学报, 2014, 29 (6): 833-844. doi: 10.3969/j.issn.1000-5781.2014.06.012ZHANG Rui, JIN Zhi-hong, XING Xi-wen, et al. Optimization of container scheduling on integrated loading and unloading operations in same ship-bay[J]. Journal of Systems Engineering, 2014, 29 (6): 833-844. (in Chinese). doi: 10.3969/j.issn.1000-5781.2014.06.012 [11] 周鹏飞, 康海贵. 面向随机环境的集装箱码头泊位-岸桥分配方法[J]. 系统工程理论与实践, 2008, 28 (1): 161-169. doi: 10.3321/j.issn:1000-6788.2008.01.024ZHOU Peng-fei, KANG Hai-gui. Study on berth and quaycrane allocation under stochastic environments in container terminal[J]. Systems Engineering—Theory and Practice, 2008, 28 (1): 161-169. (in Chinese). doi: 10.3321/j.issn:1000-6788.2008.01.024 [12] 曾庆成, 杨忠振. 集装箱码头集成调度模型与混合优化算法[J]. 系统工程学报, 2010, 25 (2): 264-270. https://www.cnki.com.cn/Article/CJFDTOTAL-XTGC201002021.htmZENG Qing-cheng, YANG Zhong-zhen. Integrating scheduling model and hybrid optimization algorithm for container terminals[J]. Journal of Systems Engineering, 2010, 25 (2): 264-270. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTGC201002021.htm [13] 孙彬, 孙俊清, 陈秋双. 基于鲁棒反应式策略的泊位和岸桥联合调度[J]. 系统工程理论与实践, 2013, 33 (4): 1076-1083. doi: 10.3969/j.issn.1000-6788.2013.04.032SUN Bin, SUN Jun-qing, CHEN Qiu-shuang. Integrated scheduling for berth and quaycranes based on robust and reactive policy[J]. Systems Engineering—Theory and Practice, 2013, 33 (4): 1076-1083. (in Chinese). doi: 10.3969/j.issn.1000-6788.2013.04.032 [14] 郑斐峰, 乔龙亮, 黄基诞. 有限预知信息下集装箱码头泊位与岸桥联合在线调度[J]. 系统管理学报, 2018, 27 (1): 1-9. https://www.cnki.com.cn/Article/CJFDTOTAL-XTGL201801001.htmZHENG Fei-feng, QIAO Long-liang, HUANG Ji-dan. An online model of berth and quay crane integrated allocation with finite look-ahead[J]. Journal of Systems and Management, 2018, 27 (1): 1-9. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTGL201801001.htm [15] SHANG Xiao-ting, CAO Jin-xin, REN Jie. A robust optimization approach to the integrated berth allocation and quay crane assignment problem[J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 94: 44-65. doi: 10.1016/j.tre.2016.06.011 [16] 杨春霞, 王诺, 杨华龙. 集装箱码头泊位-岸桥分配耦合优化[J]. 计算机集成制造系统, 2011, 17 (10): 2270-2277. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201110025.htmYANG Chun-xia, WANG Nuo, YANG Hua-long. Coupling optimization for berth allocation and quay crane assignment problem in container terminals[J]. Computer Integrated Manufacturing Systems, 2011, 17 (10): 2270-2277. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201110025.htm [17] YANG Chun-xia, WANG Xiao-jun, LI Zhen-feng. An optimization approach for coupling problem of berth allocation and quay crane assignment in container terminal[J]. Computers and Industrial Engineering, 2012, 63 (1): 243-253. doi: 10.1016/j.cie.2012.03.004 [18] 张红菊, 乐美龙. 基于多目标粒子群算法的泊位-岸桥分配研究[J]. 武汉理工大学学报, 2012, 34 (2): 59-64. doi: 10.3963/j.issn.1671-4431.2012.02.013ZHANG Hong-ju, LE Mei-long. Research on container berth-quay crane allocation based on multi-objective PSO[J]. Journal of Wuhan University of Technology, 2012, 34 (2): 59-64. (in Chinese). doi: 10.3963/j.issn.1671-4431.2012.02.013 [19] 杨华龙, 滕川川. 基于挤压算法的集装箱码头泊位与岸桥联合调度优化[J]. 大连海事大学学报, 2014, 40 (3): 8-12. doi: 10.3969/j.issn.1006-7736.2014.03.002YANG Hua-long, TENG Chuan-chuan. Extrusion algorithmbased optimization of berth and crane joint scheduling at container terminal[J]. Journal of Dalian Maritime University, 2014, 40 (3): 8-12. (in Chinese). doi: 10.3969/j.issn.1006-7736.2014.03.002 [20] LI Ming-wei, HONG Wei-chiang, GENG Jing, et al. Berth and quay crane coordinated scheduling using multi-objective chaos cloud particle swarm optimization algorithm[J]. Neural Computing and Applications, 2017, 28 (11): 3163-3182. doi: 10.1007/s00521-016-2226-7 [21] 杨春霞, 王诺. 基于多目标遗传算法的集装箱码头泊位-岸桥分配问题研究[J]. 计算机应用研究, 2010, 27 (5): 1720-1725. doi: 10.3969/j.issn.1001-3695.2010.05.032YANG Chun-xia, WANG Nuo. Berth-quay crane allocation in container terminal based on multi-objective genetic algorithm[J]. Application Research of Computers, 2010, 27 (5): 1720-1725. (in Chinese). doi: 10.3969/j.issn.1001-3695.2010.05.032 [22] JORNADA D, LEON V J. Biobjective robust optimization over the efficient set for Pareto set reduction[J]. European Journal of Operational Research, 2016, 252 (2): 573-586. doi: 10.1016/j.ejor.2016.01.017 [23] MARTNEZ-VARGAS A, DOMNGUEZ-GUERRERO J, ANDRADE A G, et al. Application of NSGA-II algorithm to the spectrum assignment problem in spectrum sharing networks[J]. Applied Soft Computing, 2016, 39: 188-198. doi: 10.1016/j.asoc.2015.11.010 [24] HU Yuan, BIE Zhao-hong, DING Tao, et al. An NSGA-II based multi-objective optimization for combined gas and electricity network expansion planning[J]. Applied Energy, 2016, 167: 280-293. doi: 10.1016/j.apenergy.2015.10.148 [25] 韩敏, 何泳. 基于高斯混沌变异和精英学习的自适应多目标粒子群算法[J]. 控制与决策, 2016, 31 (8): 1372-1378. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201608004.htmHAN Min, HE Yong. Adaptive multi-objective particle swarm optimization with Gaussian chaotic mutation and elite learning[J]. Control and Decision, 2016, 31 (8): 1372-1378. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201608004.htm [26] 李彤, 王春峰, 王文波, 等. 求解整数规划的一种仿生类全局优化算法——模拟植物生长算法[J]. 系统工程理论与实践, 2005, 25 (1): 76-85. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200501012.htmLI Tong, WANG Chun-feng, WANG Wen-bo, et al. A global optimization bionics algorithm for solving integer programming—plant growth simulation algorithm[J]. Systems Engineering—Theory and Practice, 2005, 25 (1): 76-85. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200501012.htm -





 下载:
下载: