基于线性矩阵不等式的船舶动力定位滑模控制

薛晗; 邵哲平; 潘家财; 方琼林

doi:10.19818/j.cnki.1671-1637.2018.05.012

基于线性矩阵不等式的船舶动力定位滑模控制

doi: 10.19818/j.cnki.1671-1637.2018.05.012

集美大学航海学院, 福建厦门 361021

基金项目:

国家自然科学基金项目 51579114

福建省自然科学基金项目 2018J05085

福建省中青年教师教育科研项目 JAT160273

详细信息

作者简介:
薛晗(1982-), 女, 江苏兴化人, 集美大学讲师, 工学博士, 从事智能控制研究

中图分类号: U661.33
计量
- 文章访问数: 665
- HTML全文浏览量: 155
- PDF下载量: 329
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-07
- 刊出日期: 2018-10-25

Sliding mode control for ship dynamic positioning based on linear matrix inequality

School of Navigation, Jimei University, Xiamen 361021, Fujian, China

More Information

Author Bio:
XUE Han(1982-), female, lecturer, PhD, imlmd@163.com

摘要

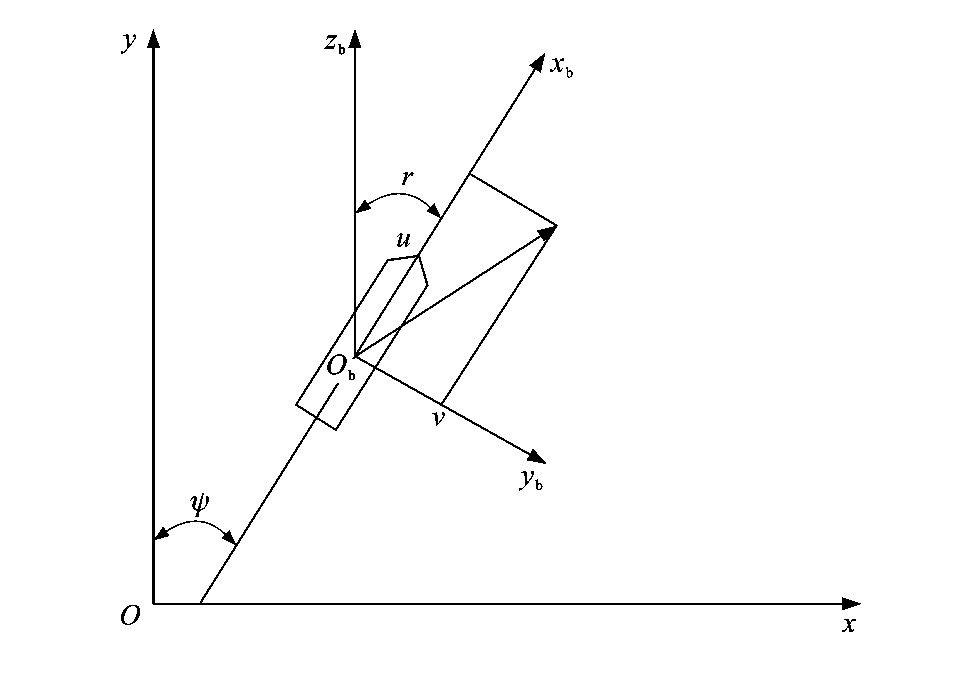
摘要: 为了解决具有非线性和环境干扰的船舶动力定位系统的控制问题, 提出了一种基于线性矩阵不等式的滑模控制算法; 将跟踪误差设计为滑模函数, 设计线性矩阵不等式, 求解状态反馈增益; 基于二次型Lyapunov函数证明了闭环系统的稳定性; 设计切换函数, 使系统对不确定性和外加干扰具有较强的鲁棒性, 避免出现抖振现象; 对基于线性矩阵不等式的滑模控制器进行仿真, 计算出动力定位船舶在无扰动的匀速运动和有外界环境扰动的变速运动2种不同情况下的前进速度、横荡速度、艏向角速度、前进加速度、横荡加速度、艏向角加速度、前进控制力、横荡控制力和艏向控制力矩等; 分析了状态反馈增益线性矩阵、边界层、切换项增益等参数对控制性能的影响。研究结果表明: 采用基本滑模控制使前进速度达到期望值所需的上升时间为29s, 而新算法为15s, 节约了48.28%;采用基本滑模控制使横荡速度达到期望值所需的上升时间为24s, 而新算法为14s, 节约了41.67%;采用基本滑模控制使艏向角速度达到期望值所需的上升时间为13s, 而新算法为10s, 节约了23.08%。可见, 设计的控制器对有非线性和环境干扰的船舶动力定位系统都具有较强的鲁棒性, 具有控制输入连续、控制抖振小、不存在过高增益等特点。
- 船舶工程 /
- 动力定位 /
- 滑模控制 /
- 线性矩阵不等式 /
- 运动控制 /
- 鲁棒性
Abstract: In order to solve the control problem of ship dynamic positioning systems with nonlinear and environmental disturbances, a sliding mode control algorithm based on the linear matrix inequality (LMI) was proposed.The tracking error was designed as a sliding mode function, and a linear matrix inequality was designed to solve the state feedback gain.Based on the quadratic Lyapunov function, the stability of the closed-loop system was proved.The switching function was designed to make the system robust to uncertainties and external disturbances and to avoid chattering.The sliding mode controller based on the LMI was simulated, and the forward speed, sway speed, heading angular speed, forward acceleration, sway acceleration, heading angular acceleration, forward control force, sway control force, and heading control moment of a dynamic-positioning ship were calculated under two different conditions, namely, uniform motion without disturbance and variable-speed motion with external environment disturbance.The effects of parameters such as the linear matrix of state feedbackgain, boundary layer, and switching gain on control performance were analyzed and compared.Analysis result indicates that it takes 29 sfor the forward speed to reach the expected value by using the basic sliding mode control, whereas the new algorithm saves 48.28% at 15 s.It takes24 sfor the sway speed to reach the expected value by using the basic sliding mode control, whereas the new algorithm saves 41.67%at 14 s.It takes 13 sfor the heading angular speed to reach the expected value by using the basic sliding mode control, whereas the new algorithm saves 23.08%at 10 s.Thus, the designed controller has strong robustness for the ship dynamic positioning system with nonlinear and environmental disturbances, and has the characteristics of continuous control input, no control chattering, and no high gain.
- ship engineering /
- dynamic positioning /
- sliding mode control /
- linear matrix inequality /
- motion control /
- robustness

HTML全文

图 1 船舶平面运动模型

Figure 1. Model of ship plane motion

下载: 全尺寸图片幻灯片

图 2 前进速度曲线

Figure 2. Forward speed curves

下载: 全尺寸图片幻灯片

图 3 横荡速度曲线

Figure 3. Sway speed curves

下载: 全尺寸图片幻灯片

图 4 艏向角速度曲线

Figure 4. Heading angular speed curves

下载: 全尺寸图片幻灯片

图 5 无扰动下控制输入曲线

Figure 5. Control input curves without disturbance

下载: 全尺寸图片幻灯片

图 6 前进加速度曲线

Figure 6. Forward acceleration curve

下载: 全尺寸图片幻灯片

图 7 横荡加速度曲线

Figure 7. Sway acceleration curve

下载: 全尺寸图片幻灯片

图 8 艏向角加速度曲线

Figure 8. Heading angular acceleration curve

下载: 全尺寸图片幻灯片

图 9 有扰动下船舶速度曲线

Figure 9. Ship speed curves with disturbance

下载: 全尺寸图片幻灯片

图 10 有扰动下控制输入曲线

Figure 10. Control input curves with disturbance

下载: 全尺寸图片幻灯片

图 11 船舶速度曲线(F₁, ₁=-28.225 0)

Figure 11. Ship speed curves (F₁, ₁=-28.225 0)

下载: 全尺寸图片幻灯片

图 12 控制输入曲线(F₁, ₁=-28.225 0)

Figure 12. Control input curves (F₁, ₁=-28.225 0)

下载: 全尺寸图片幻灯片

图 13 船舶速度曲线(F₁, ₁=-2 821.500 0)

Figure 13. Ship speed curves (F₁, ₁=-2 821.500 0)

下载: 全尺寸图片幻灯片

图 14 控制输入曲线(F₁, ₁=-2 821.500 0)

Figure 14. Control input curves (F₁, ₁=-2 821.500 0)

下载: 全尺寸图片幻灯片

图 15 船舶速度曲线(Δ=0.50)

Figure 15. Ship speed curves (Δ=0.50)

下载: 全尺寸图片幻灯片

图 16 控制输入曲线(Δ=0.50)

Figure 16. Control input curves (Δ=0.50)

下载: 全尺寸图片幻灯片

图 17 船舶速度曲线(Δ=0.02)

Figure 17. Ship speed curves (Δ=0.0.02)

下载: 全尺寸图片幻灯片

图 18 控制输入曲线(Δ=0.02)

Figure 18. Control input curves (Δ=0.02)

下载: 全尺寸图片幻灯片

图 19 船舶速度曲线(η= (100, 100, 100)^T)

Figure 19. Ship speed curves (η= (100, 100, 100)^T)

下载: 全尺寸图片幻灯片

图 20 控制输入曲线(η= (100, 100, 100)^T)

Figure 20. Control input curves (η= (100, 100, 100)^T)

下载: 全尺寸图片幻灯片

图 21 前进速度比较

Figure 21. Comparison of forward speeds

下载: 全尺寸图片幻灯片

图 22 横荡速度比较

Figure 22. Comparison of sway speeds

下载: 全尺寸图片幻灯片

图 23 艏向角速度比较

Figure 23. Comparison of heading angular speeds

下载: 全尺寸图片幻灯片

表 1 船模参数

Table 1. Ship model parameters

下载: 导出CSV

参考文献(30)

[1]	SRENSEN A J. A survey of dynamic positioning control systems[J]. Annual Reviews in Control, 2011, 35 (1): 123-136. doi: 10.1016/j.arcontrol.2011.03.008
[2]	NGUYEN T D, SRENSEN A J, QUEK S T. Design of hybrid controller for dynamic positioning from calm to extreme sea conditions[J]. Automatica, 2007, 43 (5): 768-785. doi: 10.1016/j.automatica.2006.11.017
[3]	FANG M C, LEE Z Y. Application of neuro-fuzzy algorithm to portable dynamic positioning control system for ships[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8 (1): 38-52. doi: 10.1016/j.ijnaoe.2015.09.003
[4]	PARK K P, JO A R, CHOI J W. A study on the key performance indicator of the dynamic positioning system[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8 (5): 511-518. doi: 10.1016/j.ijnaoe.2016.04.004
[5]	DU Jia-lu, HU Xin, KRSTI C'M, et al. Robust dynamic positioning of ships with disturbances under input saturation[J]. Automatica, 2016, 73 (11): 207-214.
[6]	陈士安, 王骏骋, 姚明. 车辆半主动悬架全息最优滑模控制器设计方法[J]. 交通运输工程学报, 2016, 16 (3): 72-83, 99. doi: 10.3969/j.issn.1671-1637.2016.03.009 CHEN Shi-an, WANG Jun-cheng, YAO Ming. Design method of holographic optimal sliding mode controller for semi-active suspension of vehicle[J]. Journal of Traffic and Transportation Engineering, 2016, 16 (3): 72-83, 99. (in Chinese). doi: 10.3969/j.issn.1671-1637.2016.03.009
[7]	ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Slidingmode tracking control of surface vessels[J]. IEEE Transactions on Industrial Electronics, 2008, 55 (11): 4004-4012. doi: 10.1109/TIE.2008.2005933
[8]	ROY S, KAR I N. Adaptive sliding mode control of a class of nonlinear systems with artificial delay[J]. Journal of the Franklin Institute, 2017, 354 (18): 8156-8179. doi: 10.1016/j.jfranklin.2017.10.010
[9]	刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24 (3): 407-418. doi: 10.3969/j.issn.1000-8152.2007.03.015 LIU Jin-kun, SUN Fu-chun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory and Applications, 2007, 24 (3): 407-418. (in Chinese). doi: 10.3969/j.issn.1000-8152.2007.03.015
[10]	LIU Jin-kun, SUN Fu-chun. Nominal model-based sliding mode control with backstepping for 3-axis flight table[J]. Chinese Journal of Aeronautics, 2006, 19 (1): 65-71. doi: 10.1016/S1000-9361(11)60269-0
[11]	DAI Yan-yan, KIM Y G, WEE S G, et al. Symmetric caging formation for convex polygonal object transportation by multiple mobile robots based on fuzzy sliding mode control[J]. ISA Transactions, 2016, 60: 321-332. doi: 10.1016/j.isatra.2015.11.017
[12]	邵井丰. 基于滑模变结构的船舶动力定位控制研究[D]. 大连: 大连海事大学, 2015. SHAO Jing-feng. Research on ship dynamic positioning control based on sliding mode variable structure[D]. Dalian: Dalian Maritime University, 2015. (in Chinese).
[13]	代昌盛. 欠驱动船舶运动的自适应迭代滑模控制研究[D]. 大连: 大连海事大学, 2017. DAI Chang-sheng. Research on adaptive iterative sliding mode control for underactuated ship motion[D]. Dalian: Dalian Maritime University, 2017. (in Chinese).
[14]	秦朝宇. 基于终端滑模自抗扰的船舶航迹跟踪控制[D]. 大连: 大连海事大学, 2017. QIN Chao-yu. Active disturbance rejection control for ship path following based terminal sliding mode[D]. Dalian: Dalian Maritime University, 2017. (in Chinese).
[15]	王昱棋. 基于终端滑模的欠驱动水面船舶航迹跟踪及编队控制[D]. 大连: 大连海事大学, 2017. WANG Yu-qi. Terminal sliding mode control for tracking and formation of underactuated surface vessels[D]. Dalian: Dalian Maritime University, 2017. (in Chinese).
[16]	HAN Yao-zhen, PAN Wei-gang. Gain-scheduled continuous higher-order sliding mode control for uncertain nonlinear system[J]. Optik, 2016, 127 (10): 4345-4354. doi: 10.1016/j.ijleo.2016.01.157
[17]	SUN Zhi-jian, ZHANG Guo-qing, YI Bo-wen, et al. Practical proportional integral sliding mode control for underactuated surface ships in the fields of marine practice[J]. Ocean Engineering, 2017, 142: 217-223. doi: 10.1016/j.oceaneng.2017.07.010
[18]	LIAO Yu-lei, WAN Lei, ZHUANG Jia-yuan. Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel[J]. Procedia Engineering, 2011, 15: 256-263. doi: 10.1016/j.proeng.2011.08.051
[19]	SUN Zhi-jian, ZHANG Guo-qing, LU Yu, et al. Leaderfollower formation control of underactuated surface vehicles based on sliding mode control andparameter estimation[J]. ISA Transactions, 2018, 72: 15-24. doi: 10.1016/j.isatra.2017.11.008
[20]	ESFAHANI H N, AZIMIRAD V, DANESH M. A time delay controller included terminal sliding mode and fuzzy gaintuning for underwater vehicle-manipulator systems[J]. Ocean Engineering, 2015, 107: 97-107. doi: 10.1016/j.oceaneng.2015.07.043
[21]	ZHANG Ming-jun, LIU Xing, YIN Bao-ji, et al. Adaptive terminal sliding mode based thruster fault tolerant control for underwater vehicle in time-varying ocean currents[J]. Journal of the Franklin Institute, 2015, 352 (11): 4935-4961. doi: 10.1016/j.jfranklin.2015.08.009
[22]	邹剑. 船舶航向动态滑模变结构控制研究[D]. 重庆: 重庆大学, 2012. ZOU Jian. The research of ship heading dynamic sliding variable structure control system[D]. Chongqing: Chongqing University, 2012. (in Chinese).
[23]	WANG Hui-min, YANG Guang-hong. Piecewise controller design for affine fuzzy systems via dilated linear matrix inequality characterizations[J]. ISA Transactions, 2012, 51 (6): 771-777. doi: 10.1016/j.isatra.2012.06.014
[24]	WANG Qing, XU Peng-cheng, LAM E Y, et al. Iterative solution to linear matrix inequality arising from time delay descriptor systems[J]. Applied Mathematics and Computation, 2013, 219 (9): 4176-4184. doi: 10.1016/j.amc.2012.11.017
[25]	GARONE E, NTOGRAMATZIDIS L. Linear matrix inequalities for globally monotonic tracking control[J]. Automatica, 2015, 61 (11): 173-177.
[26]	DE CAMPOSV A F, DA CRUZ J J, ZANETTA JR L C. Robust and optimal adjustment of power system stabilizers through linear matrix inequalities[J]. International Journal of Electrical Power and Energy Systems, 2012, 42 (1): 478-486. doi: 10.1016/j.ijepes.2012.04.025
[27]	BACULI J, AYOUBI M A. Fuzzy attitude control of solar sail via linear matrix inequalities[J]. Acta Astronautica, 2017, 138 (9): 233-241.
[28]	YANG Y U, DUBLJEVIC S. Linear matrix inequalities (LMIs) observer and controller design synthesis for parabolic PDE[J]. European Journal of Control, 2014, 20 (5): 227-236.
[29]	AMMAR M E, DUMONT G A. Automatic tuning of paper machines cross-direction controllers via linear matrix inequalities[J]. Journal of Electrical Systems and Information Technology, 2015, 2 (3): 283-295. doi: 10.1016/j.jesit.2015.11.006
[30]	SUN Jia, WANG Shi-heng, WANG Ke. Zhang neural networks for a set of linear matrix inequalities withtime-varying coefficient matrix[J]. Information Processing Letters, 2016, 116 (10): 603-610. doi: 10.1016/j.ipl.2016.04.014