基于双层规划的危险货物配送路径鲁棒优化

马昌喜; 何瑞春; 熊瑞琦

doi:10.19818/j.cnki.1671-1637.2018.05.016

基于双层规划的危险货物配送路径鲁棒优化

doi: 10.19818/j.cnki.1671-1637.2018.05.016

兰州交通大学交通运输学院, 甘肃兰州 730070

基金项目:

国家自然科学基金项目 71861023

详细信息

作者简介:
马昌喜(1979-), 男, 湖北汉川人, 兰州交通大学教授, 工学博士, 从事危险货物运输系统优化与设计研究

通讯作者:
何瑞春(1970-), 女, 甘肃临洮人, 兰州交通大学教授, 工学博士

中图分类号: U492.3
计量
- 文章访问数: 721
- HTML全文浏览量: 90
- PDF下载量: 478
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-26
- 刊出日期: 2018-10-25

Robust optimization on distributing routes of hazardous materials based on bi-level programming

School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China

More Information

Author Bio:
MA Chang-xi(1979-), male, professor, PhD, machangxi@mail.lzjtu.cn

Corresponding author: MA Chang-xi (1979-), male, professor, PhD, E-mail: machangxi@mail.lzjtu.cn

摘要

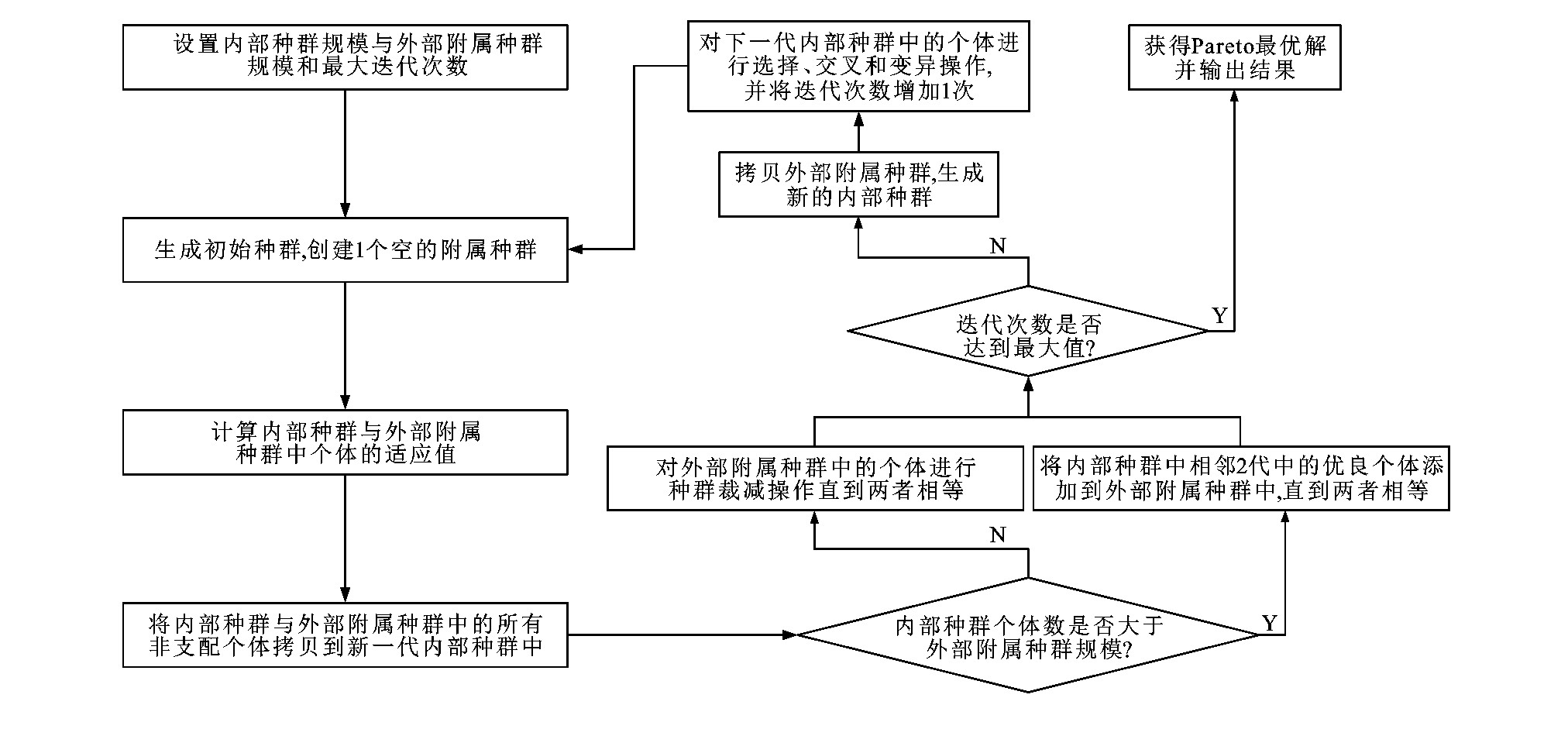
摘要: 针对不确定环境下带时间窗的多配送中心危险货物配送路径优化问题, 提出一种含鲁棒控制参数的鲁棒优化方法; 综合考虑危险货物运输风险、运输费用和服务时间窗, 构建了危险货物配送路径多目标双层鲁棒优化模型, 上层模型追求运输风险和运输费用最小化, 下层模型采用用户均衡交通分配模型; 根据Bertsimas-Sim鲁棒优化理论, 对含有不确定参数的上层模型进行鲁棒对等转化; 联合增强型Pareto遗传算法和Frank-Wolfe算法构建了求解多目标双层鲁棒优化模型的混合算法, 采用3段式编码和解码方法、等位匹配交叉操作以及翻转变异等遗传操作方法求解上层模型, 采用Frank-Wolfe算法求解下层用户均衡模型; 以经典的Sioux-Falls交通网络为例, 对含有3个配送中心、7个需求点的危险货物配送路径优化问题进行案例分析, 以验证模型及其算法的合理性。研究结果表明: 当鲁棒控制参数分别为0、30和60时, 构建的混合算法能分别快速得到3、2和3组鲁棒最优解, 且所有解均为包含具体运输路段和发车时刻的配送方案, 而非配送顺序; 该混合算法与传统两阶段启发式算法相比, 运算时间能节省54.74%。可见, 该混合算法无论是在求解效率上, 还是在解的表达形式上均优于两阶段启发式算法, 能较好地完成不确定环境下危险货物配送路径多目标双层鲁棒优化任务。
- 交通规划 /
- 危险货物 /
- 配送路径 /
- 双层规划 /
- 鲁棒模型 /
- 多目标优化 /
- 混合算法
Abstract: To solve the optimization problem for the hazardous materials distributing routes (HMDR) with multi-distribution centers and time windows in uncertain environments, a robust optimization method with robust control parameters was proposed.Comprehensively considering the transportation risk, transportation cost and service time window in hazardous materials distributing routes, a multi-objective bi-level optimization model was constructed.The upperlevel model was used to minimize the transportation risk and transportation cost.The lower-level model was constructed as the user equilibrium traffic distribution model.With the Bertsimas-Sim robust optimization theory, the robust peer-to-peer transformation was performed on the upperlevel model with uncertain parameters.The enhanced Pareto genetic algorithm and Frank-Wolfe algorithm were combined to form a hybrid algorithm to solve the multi-objective bi-level robust optimization model.The three-stage coding and decoding method, equipotent matching crossoveroperation and flipping mutation operation were used to solve the upper-level model, and the Frank-Wolfe algorithm was used to solve the lower-level model.Taking the classical Sioux-Falls transportation network as an example, a case study was conducted to verify the rationality of the model and its algorithm for the optimization on the distributing routes of hazardous materials with3 distribution centers and 7 demand points.Research result shows that when the robust control parameters are set as 0, 30 and 60, respectively, the hybrid algorithm can obtain 3, 2 and 3 robust optimal solutions, respectively, and all solutions are delivered with the specific road sections and departure times but not the distribution order.Comparing with the traditional twostage heuristic algorithm, the hybrid algorithm can save 54.74%of the runtime.It can clearly be seen that the hybrid algorithm is superior to the two-stage heuristic algorithm both in the algorithmic efficiency and expression of the solution, and can complete the multi-objective bi-level robust optimization on the hazardous materials distributing routes in uncertain environments.
- traffic planning /
- hazardous material /
- distributing route /
- bi-level programming /
- robust model /
- multi-objective optimization /
- hybrid algorithm

HTML全文

图 1 增强型Pareto遗传算法流程

Figure 1. Flow of enhanced Pareto genetic algorithm

下载: 全尺寸图片幻灯片

图 2 混合算法流程

Figure 2. Flow of hybrid algorithm

下载: 全尺寸图片幻灯片

图 3 包含12个节点的交通网络

Figure 3. Traffic network with 12nodes

下载: 全尺寸图片幻灯片

图 4 编码与解码

Figure 4. Encoding and decoding

下载: 全尺寸图片幻灯片

图 5 交叉操作

Figure 5. Crossover operation

下载: 全尺寸图片幻灯片

图 6 变异操作

Figure 6. Mutation operation

下载: 全尺寸图片幻灯片

图 7 Sioux-Falls网络

Figure 7. Sioux-Falls network

下载: 全尺寸图片幻灯片

图 8 初始种群分布

Figure 8. Initial population distribution

下载: 全尺寸图片幻灯片

图 9 进化150代后种群分布

Figure 9. Population distribution after 150evolution generations

下载: 全尺寸图片幻灯片

表 1 运输任务信息

Table 1. Information of transport task

下载: 导出CSV

表 2 路段相关参数取值

Table 2. Values of related road parameters

下载: 导出CSV

表 3 λ=0时的Pareto解集

Table 3. Pareto solution sets when λ=0

下载: 导出CSV

表 4 λ=30时的Pareto解集

Table 4. Pareto solution sets when λ=30

下载: 导出CSV

表 5 λ=60时的Pareto解集

Table 5. Pareto solution sets when λ=60

下载: 导出CSV

表 6 λ=0时采用不同算法得到的配送方案对比

Table 6. Comparison of distribution schemes based on different algorithms when λ=0

下载: 导出CSV

参考文献(34)

[1]	胡大伟, 陈希琼, 高扬. 定位路径问题综述[J]. 交通运输工程学报, 2018, 18 (1): 111-129. doi: 10.3969/j.issn.1671-1637.2018.01.011 HU Da-wei, CHEN Xi-qiong, GAO Yang. Review on locationrouting problem[J]. Journal of Traffic and Transportation Engineering, 2018, 18 (1): 111-129. (in Chinese). doi: 10.3969/j.issn.1671-1637.2018.01.011
[2]	VERMA M. A cost and expected consequence approach to planning and managing railroad transportation of hazardous materials[J]. Transportation Research Part D: Transport and Environment, 2009, 14 (5): 300-305. doi: 10.1016/j.trd.2009.03.002
[3]	JASSBI J, MAKVANDI P. Route selection based on soft MODM framework in transportation of hazardous materials[J]. Applied Mathematical Sciences, 2010, 4 (63): 3121-3132.
[4]	BIANCO L, CARAMIA M, GIORDANI S. A bilevel flow model for hazmat transportation network design[J]. Transportation Research Part C: Emerging Technologies, 2009, 17 (2): 175-196. doi: 10.1016/j.trc.2008.10.001
[5]	MINCIARDI R, ROBBA M. A bi-level approach for the decentralized optimal control of dangerous goods fleets flowing through a tunnel[C]//IFAC. Preprints of the 18th IFAC World Congress. Laxenburg: IFAC, 2011: 9788-9793.
[6]	KHEIRKHAH A, NAVIDI H, BIDGOLI M M. A bi-level network interdiction model for solving the hazmat routing problem[J]. International Journal of Production Research, 2017, 54 (2): 459-471.
[7]	CHIOU S W. A risk-averse signal setting policy for regulating hazardous material transportation under uncertain travel demand[J]. Transportation Research Part D: Transport and Environment, 2017, 50: 446-472. doi: 10.1016/j.trd.2016.11.029
[8]	DU Jiao-man, LI Xiang, YU Le-an, et al. Multi-depot vehicle routing problem for hazardous materials transportation: a fuzzy bilevel programming[J]. Information Sciences, 2017, 399: 201-218. doi: 10.1016/j.ins.2017.02.011
[9]	XIN C L, QINGGE L, WANG J M, et al. Robust optimization for the hazardous materials transportation network design problem[J]. Journal of Combinatorial Optimization, 2015, 30: 320-334. doi: 10.1007/s10878-014-9751-z
[10]	贾红梅. 公路危险品运输决策策略研究[D]. 长春: 吉林大学, 2006. JIA Hong-mei. The study of road hazmat transportation strategies[D]. Changchun: Jilin University, 2006. (in Chinese).
[11]	帅斌, 种鹏云. 基于决策者风险偏好的危险货物运输路径优化问题研究[J]. 铁道货运, 2011, 28 (1): 7-13. https://www.cnki.com.cn/Article/CJFDTOTAL-TDHY201101004.htm SHUAI Bin, ZHONG Peng-yun. Research on routing optimization of hazardous material transportation based on risk preference of decision maker[J]. Railway Freight Transport, 2011, 28 (1): 7-13. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDHY201101004.htm
[12]	王云鹏, 孙文财, 李世武, 等. 基于ArcGIS的危险品城市运输路径优化模型[J]. 吉林大学学报: 工学版, 2009, 39 (1): 45-49. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY200901009.htm WANG Yun-peng, SUN Wen-cai, LI Shi-wu, et al. Route optimization model for urban hazardous material transportation based on ArcGIS[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39 (1): 45-49. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY200901009.htm
[13]	马昌喜, 广晓平, 吴芳, 等. 发达运输网络环境下危险品公路运输路径决策[J]. 交通运输系统工程与信息, 2009, 9 (4): 134-139. doi: 10.3969/j.issn.1009-6744.2009.04.021 MA Chang-xi, GUANG Xiao-ping, WU Fang, et al. Highway transportation route decision-making of hazardous material in developed transportation network[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9 (4): 134-139. (in Chinese). doi: 10.3969/j.issn.1009-6744.2009.04.021
[14]	熊瑞琦, 马昌喜. 多配送中心危险货物配送路径鲁棒优化[J]. 计算机应用, 2017, 37 (5): 1485-1490. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201705049.htm XIONG Rui-qi, MA Chang-xi. Robust vehicle route optimization for multi-depot hazardous materials transportation[J]. Journal of Computer Applications, 2017, 37 (5): 1485-1490. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201705049.htm
[15]	马昌喜. 危险品道路运输网络优化设计研究[D]. 兰州: 兰州交通大学, 2013. MA Chang-xi. Study on the optimization design of hazardous materials road transportation network[D]. Lanzhou: Lanzhou Jiaotong University, 2013. (in Chinese).
[16]	代存杰, 李引珍, 马昌喜, 等. 考虑风险分布特征的危险品运输路径优化[J]. 中国公路学报, 2018, 31 (4): 330-342. doi: 10.3969/j.issn.1001-7372.2018.04.038 DAI Cun-jie, LI Yin-zhen, MA Chang-xi, et al. Transportation path optimization for hazardous materials considering characteristics of risk distribution[J]. China Journal of Highway and Transport, 2018, 31 (4): 330-342. (in Chinese). doi: 10.3969/j.issn.1001-7372.2018.04.038
[17]	MA Chang-xi, LI Yin-zhen, HE Rui-chun, et al. Route optimisation models and algorithms for hazardous materials transportation under different environments[J]. International Journal of Bio-Inspired Computation, 2013, 5 (4): 252-264. doi: 10.1504/IJBIC.2013.055473
[18]	陆键, 刘禹杰, 马晓丽. 基于博弈论的危险品运输网络选线[J]. 中国公路学报, 2018, 31 (4): 322-329. doi: 10.3969/j.issn.1001-7372.2018.04.037 LU Jian, LIU Yu-jie, MA Xiao-li. Game-theory-based hazardous materials transport network routing[J]. China Journal of Highway and Transport, 2018, 31 (4): 322-329. (in Chinese). doi: 10.3969/j.issn.1001-7372.2018.04.037
[19]	张逊逊, 许宏科, 于加晴. 融合PM_2.5排放量和运输路程的区域[J]. 长安大学学报: 自然科学版, 2017, 37 (2): 99-106. doi: 10.3969/j.issn.1671-8879.2017.02.012 ZHANG Xun-xun, XU Hong-ke, YU Jia-qing. Path decision-making of regional agricultural products distribution with fusion of PM_2.5emissions and transportation distance[J]. Journal of Chang'an University: Natural Science Edition, 2017, 37 (2): 99-106. (in Chinese). doi: 10.3969/j.issn.1671-8879.2017.02.012
[20]	MA Chang-xi, HAO Wei, PAN Fu-quan, et al. Road screening and distribution route multi-objective robust optimization for hazardous materials based on neural network and genetic algorithm[J]. Plos One, 2018, 13 (6): 1-22.
[21]	BERTSIMAS D, SIM M. The price of robustness[J]. Operations Research, 2004, 52 (1): 35-53. doi: 10.1287/opre.1030.0065
[22]	王秋平, 丁猛. 历史街区交通微循环优化的双层规划模型[J]. 交通运输工程学报, 2016, 16 (3): 125-132. http://transport.chd.edu.cn/article/id/201603015 WANG Qiu-ping, DING Meng. Bi-level programming model for traffic microcirculation optimization in historic districts[J]. Journal of Traffic and Transportation Engineering, 2016, 16 (3): 125-132. (in Chinese). http://transport.chd.edu.cn/article/id/201603015
[23]	MA Chang-xi, HAO Wei, HE Rui-chun, et al. Distribution path robust optimization of electric vehicle with multiple distribution centers[J]. Plos One, 2018, 13 (3): 1-16.
[24]	代存杰, 李引珍, 马昌喜, 等. 时间依赖需求下多车型快速公交发车频率优化[J]. 交通运输工程学报, 2017, 17 (1): 129-139. http://transport.chd.edu.cn/article/id/201701015 DAI Cun-jie, LI Yin-zhen, MA Chang-xi, et al. Optimization of departure frequency for bus rapid transit with multi-type vehicles under time-dependent demand[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (1): 129-139. (in Chinese). http://transport.chd.edu.cn/article/id/201701015
[25]	MA Chang-xi, HE Rui-chun, ZHANG Wei. Path optimization of taxi carpooling[J]. Plos One, 2018, 13 (8): 1-15.
[26]	杨临涧, 赵祥模, 贺冰花, 等. 随机用户均衡交通分配问题的蚁群优化算法[J]. 交通运输工程学报, 2018, 18 (3): 189-198. http://transport.chd.edu.cn/article/id/201803019 YANG Lin-jian, ZHAO Xiang-mo, HE Bing-hua, et al. An ant colony optimization algorithm of stochastic user equilibrium traffic assignment problem[J]. Journal of Traffic and Transportation Engineering, 2018, 18 (3): 189-198. (in Chinese). http://transport.chd.edu.cn/article/id/201803019
[27]	杨忠振, 穆雪, 朱晓聪. 交通流变化下的多配送中心-多需求点配送网络优化模型[J]. 交通运输工程学报, 2015, 15 (1): 100-107. doi: 10.19818/j.cnki.1671-1637.2015.01.013 YANG Zhong-zhen, MU Xue, ZHU Xiao-cong. Optimization model of distribution network with multiple distribution centers and multiple demand points considering traffic flow change[J]. Journal of Traffic and Transportation Engineering, 2015, 15 (1): 100-107. (in Chinese). doi: 10.19818/j.cnki.1671-1637.2015.01.013
[28]	TANG Jin-jun, YANG Yi-fan, QI Yong. A hybrid algorithm for urban transit schedule optimization[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 512: 745-755.
[29]	贺韵竹, 杨忠振. 自营货车与公交车协同快件配送优化[J]. 交通运输工程学报, 2017, 17 (6): 97-103. http://transport.chd.edu.cn/article/id/201706011 HE Yun-zhu, YANG Zhong-zhen. Optimization of express distribution by cooperatively using private trucks and buses[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (6): 97-103. (in Chinese). http://transport.chd.edu.cn/article/id/201706011
[30]	汪宏晨, 张霞, 唐炉亮, 等. 时段交通限行的时空动态建模与路径优化方法[J]. 长安大学学报: 自然科学版, 2017, 37 (5): 89-96. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201705012.htm WANG Hong-chen, ZHANG Xia, TANG Lu-liang, et al. Time and space dynamic modeling and route optimization method of time-dependent traffic restriction[J]. Journal of Chang'an University: Natural Science Edition, 2017, 37 (5): 89-96. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201705012.htm
[31]	郭咏梅, 胡大伟, 陈翔. 改进蚁群算法求解带时间窗的应急物流开环车辆路径问题[J]. 长安大学学报: 自然科学版, 2017, 37 (6): 105-112. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201706015.htm GUO Yong-mei, HU Da-wei, CHEN Xiang. Solution of emergency logistics open-loop vehicle routing problem with time window based on improved ant colony algorithm[J]. Journal of Chang'an University: Natural Science Edition, 2017, 37 (6): 105-112. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201706015.htm
[32]	叶清. 危险品运输车辆鲁棒调度模型与算法研究[D]. 兰州: 兰州交通大学, 2016. YE Qing. Research on model and algorithm for hazardous materials transport vehicle robust scheduling[D]. Lanzhou: Lanzhou Jiaotong University, 2016. (in Chinese).
[33]	SUWANSIRIKUL C, FRIESZ T L, TOBIN R L. Equilibrium decomposed optimization: a heuristic for the continuous equilibrium network design problem[J]. Transportation Science, 1987, 21 (4): 254-263.
[34]	于滨, 靳鹏欢, 杨忠振. 两阶段启发式算法求解带时间窗的多中心车辆路径问题[J]. 系统工程理论与实践, 2012, 32 (8): 1793-1800. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201208021.htm YU Bin, JIN Peng-huan, YANG Zhong-zhen. Two-stage heuristic algorithm for multi-depot vehicle routing problem with time windows[J]. Systems Engineering—Theory and Practice, 2012, 32 (8): 1793-1800. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL201208021.htm