Application of bilinear cohesive zone model in damage and cracking analysis of concrete pavement
-
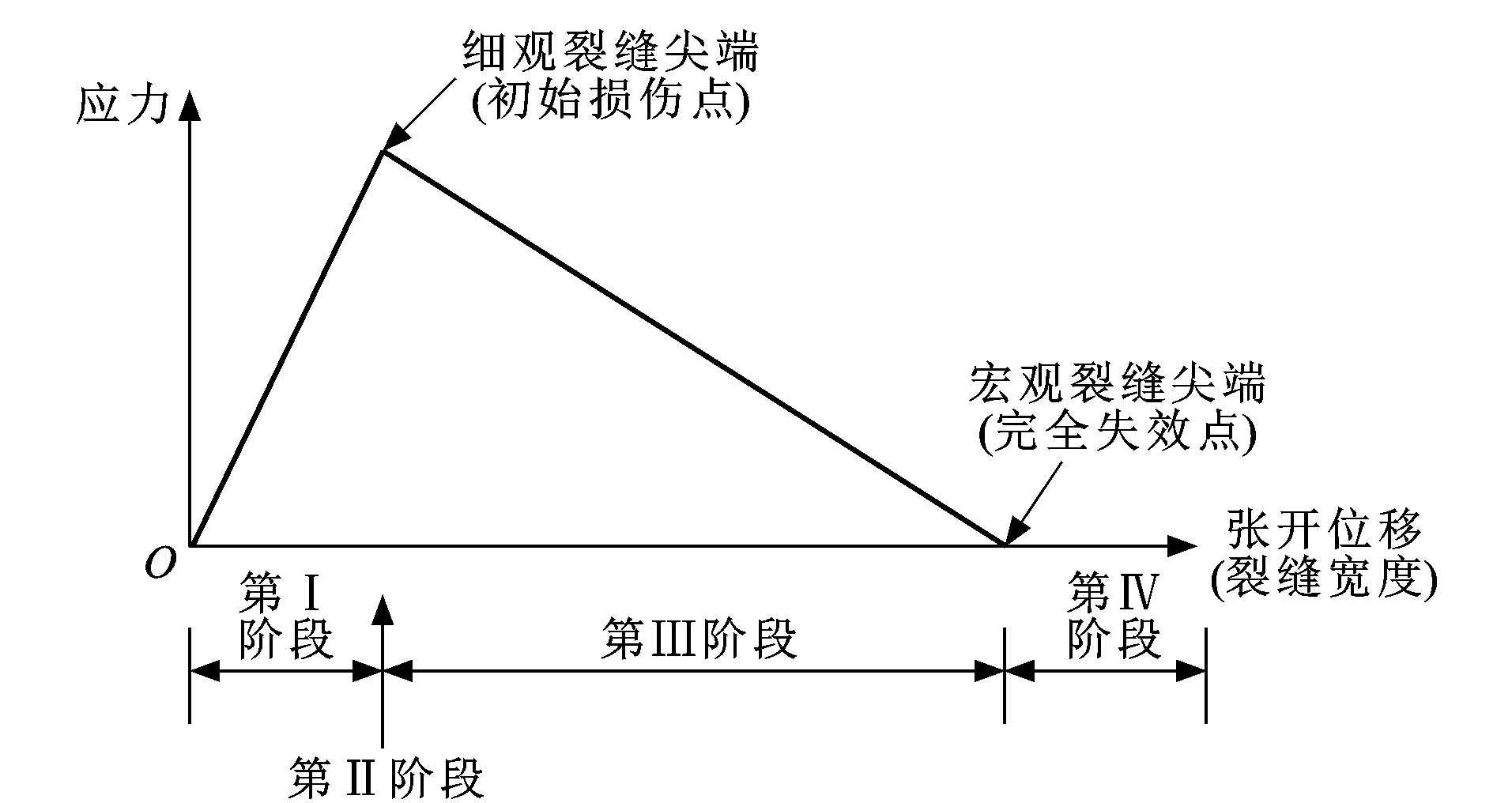
摘要: 为了揭示混凝土路面的损伤开裂机理及其对承载力的影响, 考虑混凝土材料的弹塑性, 应用非线性断裂力学中的双线性黏聚区模型, 结合ABAQUS有限元软件, 在预计开裂部位布设黏结单元, 模拟了四点加载小梁试件从弹性响应到断裂失效的全过程, 以验证双线性黏聚区模型在混凝土损伤开裂分析中的适用性; 应用双线性黏聚区模型分析了Winkler地基上混凝土板的断裂特性和损伤后的承载力衰减。分析结果表明: 在加载小梁受荷全过程中, 梁底应力经历了线性增大、达到混凝土极限强度后减小、最大点上移与变为0等阶段, 作用力-加载位移变化与已有研究一致; 在加载全过程中, 混凝土板的截面应力分布变化与小梁类似; 混凝土板在损伤阶段承载力会持续增大, 但由于板的支承条件与四点加载小梁不同, 板的断裂近似于脆性断裂, 无明显承载力衰减过程, 板断裂时的极限承载力与弹性阶段临界状态承载力之比为1.32;混凝土板发生初始损伤后, 极限承载力最大会衰减至未损伤板的87%, 且随着初始损伤程度的增加, 极限承载力衰减速率变大。Abstract: In order to reveal the damage and cracking mechanisms and their impact on the bearing capacity of concrete pavement, the elasticity and plasticity of concrete material were considered. By using the bilinear cohesive zone model in non-linear fracture mechanics, the cohesive elements were inserted into the potential path of crack propagation based on ABAQUS finite element software, and the whole process from elastic response to damage failure was modeled for a four-point loading beam. The reliability of bilinear cohesive zone model for the analysis of concrete damage and cracking was verified. By using the bilinear cohesive zone model, the cracking characteristics and the decrease of bearing capacity after the initial damage of a concrete slab on Winkler foundation were analyzed as well. Analysis result indicates that under the entire process of loading, the stresses at the bottom of the beam experience the phases of increasing linearly, decreasing after reaching the concrete flexural strength, the maximum stress point moving upwards, and reducing to 0. The load-displacement relationship on the beam is in accordance to the existing results. For the concrete slab under the entire process of loading, the variations of stress distribution at the section are similar to those of the beam. The bearing capacity of concrete slab increases continuously, but for its supporting condition is different from that of the beam. The failure of concrete slab appears to be brittle, and shows no obvious decay. The ratio of the ultimate bearing capacity to the critical bearing capacity at the elastic phase is 1.32. Once the initial damage of concrete slab occurs, the ultimate bearing capacity will decrease at most to 87% of undamaged slab. The decay rate of ultimate bearing capacity increases with the degree of initial damage.
-
图 4 弹性阶段梁截面正应力分布
Figure 4. Normal stress distributions along beam section at elasticity stage
图 5 损伤阶段梁截面正应力分布
Figure 5. Normal stress distributions along beam section at damage stage
图 6 开裂阶段梁截面正应力分布
Figure 6. Normal stress distributions along beam section at cracking stage
图 10 初始损伤板与未损伤板的极限应力之比
Figure 10. Ratioes of ultimate stress of slab with initial damage to that of undamaged slab
表 1 混凝土材料参数
Table 1. Concrete material parameters
参数 数值 弹性模量/GPa 32.04 泊松比 0.15 抗拉强度/MPa 4.15 断裂能/ (N·m-1) 167 开裂位移/mm 0.076 2 
下载: 导出CSV
-
[1] XIAO Yang-jian, CHEN Zeng-shun, ZHOU Jian-ting, et al. Concrete plastic-damage factor for finite element analysis: concept, simulation, and experiment[J]. Advances in Mechanical Engineering, 2017, 9 (9): 1-10. [2] IOANNIDES A M. Fracture mechanics in pavement engineering: the specimen-size effect[J]. Transportation Research Record, 1997 (1568): 10-16. [3] RAMSAMOOJ D V, LIN G S, RAMADAN J. Stresses at joints and cracks in highway and airport pavements[J]. Engineering Fracture Mechanics, 1998, 60: 507-518. doi: 10.1016/S0013-7944(98)00059-9 [4] CASTELL M A, INGRAFFEA A R, IRWIN L H. Fatigue crack growth in pavements[J]. Journal of Transportation Engineering, 2000, 126 (4): 283-290. doi: 10.1061/(ASCE)0733-947X(2000)126:4(283) [5] JENSEN E A, HANSEN W. Crack resistance of jointed plain concrete pavements[J]. Transportation Research Record, 2002 (1809): 60-65. [6] IOANNIDES A M, PENG Jun, SWINDLER JR J R. ABAQUS model for PCC slab cracking[J]. International Journal of Pavement Engineering, 2006, 7 (4): 311-321. doi: 10.1080/10298430600798994 [7] GAEDICKE C, ROESLER J, SHAH S. Fatigue crack growth prediction in concrete slabs[J]. International Journal of Fatigue, 2009, 31: 1309-1317. doi: 10.1016/j.ijfatigue.2009.02.040 [8] AMERI M, MANSOURIAN A, KHAVAS M H, et al. Cracked asphalt pavement under traffic loading—a 3D finite element analysis[J]. Engineering Fracture Mechanics, 2011, 78 (8): 1817-1826. doi: 10.1016/j.engfracmech.2010.12.013 [9] LING Jian-ming, TAO Ze-feng, QIAN Jin-song, et al. Investigation the influences of geotextile on reducing the thermal reflective cracking using XFEM[J]. International Journal of Pavement Engineering, 2018, 19 (5): 391-398. doi: 10.1080/10298436.2017.1402598 [10] JENQ Y, SHAH S P. Two parameter fracture model for concrete[J]. Journal of Engineering Mechanics, 1985, 111 (10): 1227-1241. doi: 10.1061/(ASCE)0733-9399(1985)111:10(1227) [11] BARENBLATT G I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks[J]. Journal of Applied Mathematics and Mechanics, 1959, 23 (3): 622-636. doi: 10.1016/0021-8928(59)90157-1 [12] BARENBLATT G I. The mathematical theory of equilibrium cracks in brittle fracture[J]. Advances in Applied Mechanics, 1962, 7: 55-129. [13] HILLERBORG A, MODEER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6 (6): 773-781. doi: 10.1016/0008-8846(76)90007-7 [14] BRINCKER R, DAHL H. Fictitious crack model of concrete fracture[J]. Magazine of Concrete Research, 1989, 41 (147): 79-86. doi: 10.1680/macr.1989.41.147.79 [15] ULFKJæR J P, KRENK S, BRINCKER R. Analytical model for fictitious crack propagation in concrete beams[J]. Journal of Engineering Mechanics, 1995, 121 (1): 7-15. doi: 10.1061/(ASCE)0733-9399(1995)121:1(7) [16] ELICES M, GUINEA G V, GOMEZ J, et al. The cohesive zone model: advantages, limitations and challenges[J]. Engineering Fracture Mechanics, 2002, 69 (2): 137-163. doi: 10.1016/S0013-7944(01)00083-2 [17] SONG S H, PAULINO G H, BUTTLAR W G. Simulation of crack propagation in asphalt concrete using an intrinsic cohesive zone model[J]. Journal of Engineering Mechanics, 2006, 132 (11): 1215-1223. doi: 10.1061/(ASCE)0733-9399(2006)132:11(1215) [18] SONG S H, PAULINO G H, BUTTLAR W G. A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material[J]. Engineering Fracture Mechanics, 2006, 73 (18): 2829-2848. doi: 10.1016/j.engfracmech.2006.04.030 [19] ROESLER J, PAULINO G H, PARK K, et al. Concrete fracture prediction using bilinear softening[J]. Cement and Concrete Composites, 2007, 29 (4): 300-312. doi: 10.1016/j.cemconcomp.2006.12.002 [20] FERREIRA M D C, VENTURINI W S, HILD F. On the analysis of notched concrete beams: from measurement with digital image correlation to identification with boundary element method of a cohesive model[J]. Engineering Fracture Mechanics, 2011, 78 (1): 71-84. doi: 10.1016/j.engfracmech.2010.10.008 [21] KIM Y R. Cohesive zone model to predict fracture in bituminous materials and asphaltic pavements: state-of-the-art review[J]. International Journal of Pavement Engineering, 2011, 12 (4): 343-356. doi: 10.1080/10298436.2011.575138 [22] 周正峰, 蒲卓桁, 刘超. 黏聚区模型在沥青路面反射裂缝模拟中的应用[J]. 交通运输工程学报, 2018, 18 (3): 1-10. doi: 10.3969/j.issn.1671-1637.2018.03.002ZHOU Zheng-feng, PU Zhuo-heng, LIU Chao. Application of cohesive zone model to simulate reflective crack of asphalt pavement[J]. Journal of Traffic and Transportation Engineering, 2018, 18 (3): 1-10. (in Chinese). doi: 10.3969/j.issn.1671-1637.2018.03.002 [23] ROESLERJ, PAULINO G, GAEDICKE C, et al. Fracture behavior of functionally graded concrete materials for rigid pavements[J]. Transportation Research Record, 2007 (2037): 40-50. [24] PARK K, PAULINO G H, ROESLER J R. Determination of the kink point in the bilinear softening model for concrete[J]. Engineering Fracture Mechanics, 2008, 75 (13): 3806-3818. doi: 10.1016/j.engfracmech.2008.02.002 [25] PARK K, PAULINO G H, ROESLER JR. Cohesive fracture model for functionally graded fiber reinforced concrete[J]. Cement and Concrete Reseach, 2010, 40: 956-965. doi: 10.1016/j.cemconres.2010.02.004 [26] GAEDICKE C, ROESLER J. Fracture-based method to determine flexural capacity of concrete beams on soil[J]. Road Materials and Pavement Design, 2010, 11 (2): 361-385. doi: 10.1080/14680629.2010.9690280 [27] GAEDICKE C, ROESLER J, EVANGELISTA JR F. Three-dimensional cohesive crack model prediction of the flexural capacity of concrete slabs on soil[J]. Engineering Fracture Mechanics, 2012, 94: 1-12. doi: 10.1016/j.engfracmech.2012.04.029 [28] 管俊峰, 卿龙邦, 赵顺波. 混凝土三点弯曲梁裂缝断裂全过程数值模拟研究[J]. 计算力学学报, 2013, 30 (1): 143-148, 155. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG201301023.htmGUAN Jun-feng, QING Long-bang, ZHAO Shun-bo. Research on numerical simulation on the whole cracking processes of three-point bending notch concrete beams[J]. Chinese Journal of Computational Mechanics, 2013, 30 (1): 143-148, 155. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG201301023.htm [29] LU W Y, HU S W. Effect of large crack-depth ratio on three-point bending concrete beam with single edge notch[J]. Materials Research Innovations, 2015, 19 (S8): 312-317. [30] CAMANHO P P, DAVILA C G. Mix-mode decohesion finite elements for the simulation of delamination in composite materials[R]. Washington DC: NASA, 2002. -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 1514
- HTML全文浏览量: 271
- PDF下载量: 1025
- 被引次数: 0
