基于非线性Drive-shaft模型的车辆传动系统冲击响应

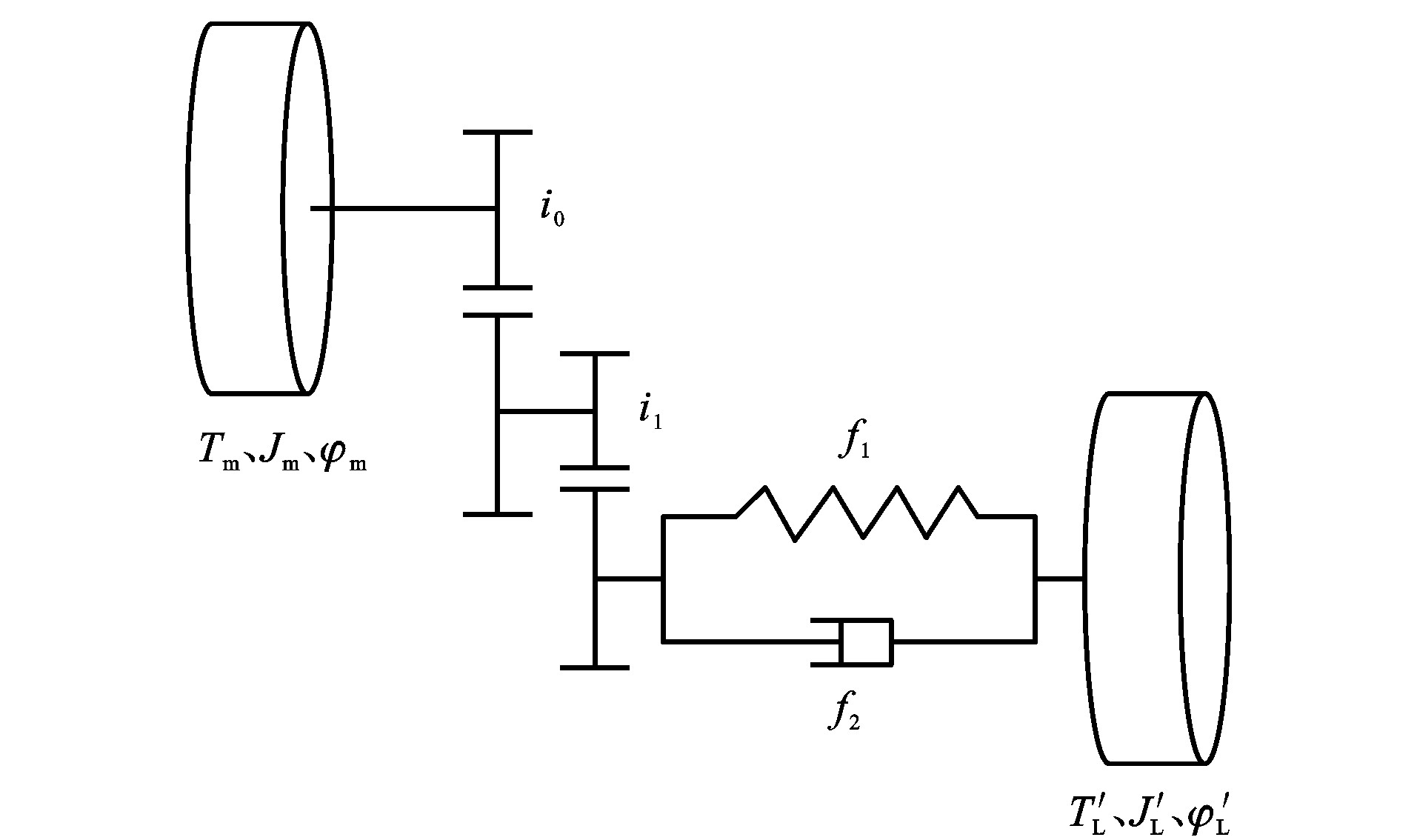
摘要: 建立了包含线性与非线性项的车辆传动系统非线性Drive-shaft模型, 应用具有耗散项的拉格朗日方程将非线性Drive-shaft模型转换为当量化的两质量模型, 通过将两端扭转角等效到同一端获得了传动系统的冲击响应方程, 应用Routh-Hurwitz准则分析了冲击响应方程的稳定性, 获得了稳定性参数区间。仿真结果表明: 将非线性阻尼分别设置为0和线性阻尼的1/10、-1/10时, 冲击响应首个峰值的绝对值分别为0.153 9、0.101 4、0.371 6, 当非线性阻尼为线性阻尼的1/10时, 冲击响应的首个峰值的绝对值最小, 这说明正的非线性阻尼有利于冲击响应的衰减; 将非线性刚度分别设置为0和线性刚度的1/10、-1/10时, 获得的冲击响应首个峰值的绝对值分别为0.153 9、0.178 8、0.115 9, 当非线性刚度为线性刚度的-1/10时, 冲击响应的首个峰值的绝对值最小, 这说明负的三次方非线性刚度有利于冲击响应的衰减; 在固定非线性刚度为线性刚度的-1/10的基础上, 将代表非线性阻尼的系数分别设置为0.1、0、-0.1, 获得的冲击响应首个峰值的绝对值分别为0.078 4、0.114 2、0.231 6。可见, 当代表非线性阻尼的系数设置为0.1时, 冲击响应的首个峰值的绝对值最小, 这表明在传动系统线性刚度及线性阻尼的基础上, 设计负的非线性刚度及正的非线性阻尼可以提升传动系统抵抗冲击的性能。
- 汽车工程 /
- Drive-shaft模型 /
- 传动系统 /
- 非线性刚度 /
- 非线性阻尼 /
- 冲击响应 /
- 稳定性
Abstract: The nonlinear drive-shaft model of the vehicle powertrain that consists of linear and nonlinear terms was established. Based on the Lagrange equation with dissipative terms, the quantized two-mass model was obtained from the nonlinear drive-shaft model. The shock response equation was obtained by the equivalent torsion angle from two ends of the powertrain to one end. The stability of the shock response equation, as well as the stable region of the parameters, were obtained by using the Routh-Hurwitz criterion. Simulation result shows that when the values of the nonlinear damping are set as 0, 1/10, and-1/10 of the linear damping, the absolute values of the first peak of shock response are 0.153 9, 0.101 4, and 0.371 6, respectively. When the value of the nonlinear damping is 1/10 of the linear damping, the absolute value of the first peak is the smallest, which indicates that the positive nonlinear damping is beneficial to the shock response. When the values of nonlinear stiffness are set as 0, 1/10, and-1/10 of the linear stiffness, the absolute values of the first peak of the shock response are 0.153 9, 0.178 8, and 0.115 9, respectively. When the value of nonlinear stiffness is-1/10 of the linear stiffness, the absolute value of the first peak is the smallest, which indicates that the negative cubic nonlinear stiffness is beneficial to shock response. When the value of nonlinear stiffness is fixed at-1/10 of linear stiffness and the coefficients that represent the nonlinear damping are set as 0.1, 0, and-0.1, respectively, the absolute values of the first peak are obtained as 0.078 4, 0.114 2, and 0.231 6, respectively. When the coefficient representing the nonlinear damping is set as 0.1, the absolute value of the first peak of the shock response is the smallest, which indicates that, on the basis of the linear stiffness and damping of the powertrain system, the shock resistance of the powertrain can be improved by introducing negative nonlinear cubic stiffness and positive nonlinear damping to the linear powertrain.
- automotive engineering /
- drive-shaft model /
- powertrain /
- nonlinear stiffness /
- nonlinear damping /
- shock response /
- stability

HTML全文

图 1 传动系统Drive-shaft模型

Figure 1. Drive-shaft model of powertrain

下载: 全尺寸图片幻灯片

图 2 不同非线性阻尼下的冲击响应曲线

Figure 2. Shock response curves under different nonlinear dampings

下载: 全尺寸图片幻灯片

图 3 不同非线性阻尼下的幅频响应曲线

Figure 3. Amplitude-frequency response curves under different nonlinear dampings

下载: 全尺寸图片幻灯片

图 4 不同非线性刚度下的冲击响应曲线

Figure 4. Shock response curves under different nonlinear stiffnesses

下载: 全尺寸图片幻灯片

图 5 不同非线性刚度下的幅频响应曲线

Figure 5. Amplitude-frequency response curves under different nonlinear stiffnesses

下载: 全尺寸图片幻灯片

图 6 非线性刚度与非线性阻尼下的传动系统冲击响应曲线

Figure 6. Shock response curves of powertrain under nonlinear stiffnesses and nonlinear dampings

下载: 全尺寸图片幻灯片

图 7 非线性刚度与非线性阻尼下的传动系统幅频响应曲线

Figure 7. Amplitude-frequency response curves of powertrain under nonlinear stiffnesses and nonlinear dampings

下载: 全尺寸图片幻灯片

参考文献(31)

[1]	LI Lai-hang, SINGH R. Analysis of start-up transient for a powertrain system with a nonlinear clutch damper[J]. Mechanical Systems and Signal Processing, 2015, 62-63: 460-479. doi: 10.1016/j.ymssp.2015.03.001
[2]	LI Meng, KHONSARI M, YANG Ru-zhou. Dynamics analysis of torsional vibration induced by clutch and gear set in automatic transmission[J]. International Journal of Automotive Technology, 2018, 19 (3): 473-488. doi: 10.1007/s12239-018-0046-8
[3]	FAN Xin-xiu, WALKER P D, WANG Qi. Modeling and simulation of longitudinal dynamics coupled with clutch engagement dynamics for ground vehicles[J]. Multibody System Dynamics, 2018, 43 (2): 153-174. doi: 10.1007/s11044-017-9592-5
[4]	YANG Li-kun, LI He-yan, AHMADIAN M, et al. Analysis of the influence of engine torque excitation on clutch judder[J]. Journal of Vibration and Control, 2017, 23 (4): 645-655. doi: 10.1177/1077546315582291
[5]	TURNBULL R, MIKNAS O, MOHAMMDAPOUR M, et al. Combined experimental and flexible multi-body dynamic investigation of high-energy impact-induced driveline vibration[J]. Proceeding of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2017, 231 (1): 181-193. doi: 10.1177/1464419316659996
[6]	WANG Yong-liang, QIN Xun-peng, HUANG Song, et al. Design and analysis of a multi-stage torsional stiffness dual mass flywheel based on vibration control[J]. Applied Acoustics, 2016, 104: 172-181. doi: 10.1016/j.apacoust.2015.11.004
[7]	TAILONY R, NIKOLAIDIS E. Driveline backlash identification and torsional defects detection using torque signatures analysis for an IC engine cold test stand[J]. Journal of Failure Analysis and Prevention, 2017, 17 (6): 1226-1233. doi: 10.1007/s11668-017-0361-9
[8]	TAILONY R, NIKOLAIDIS E. Designing an external collar torsional damper based on the backlash excitation measurements and the calculated torsional elastic properties of the engine cold test driveline[J]. Journal of Failure Analysis and Prevention, 2018, 18 (1): 130-135. doi: 10.1007/s11668-018-0390-z
[9]	IDEHARA S J, FLACH F L, LEMES D. Modeling of nonlinear torsional vibration of the automotive powertrain[J]. Journal of Vibration and Control, 2018, 24 (9): 1774-1786. doi: 10.1177/1077546316668687
[10]	VADAMALU R S, BEIDL C. MPC for active torsional vibration reduction of hybrid electric powertrains[J]. IFAC Papers OnLine, 2016, 49 (11): 756-761. doi: 10.1016/j.ifacol.2016.08.110
[11]	LIU Dong-hao, YU Hai-sheng, ZHANG Jian-wu. Multibody dynamics analysis for the coupled vibrations of a power split hybrid electric vehicle during the engine start transition[J]. Proceeding of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2016, 230 (4): 527-540. doi: 10.1177/1464419315618862
[12]	HE Hong-wen, GUO Xiao-guang. Multi-objective optimization research on the start condition for a parallel hybrid electric vehicle[J]. Applied Energy, 2018, 227: 294-303. doi: 10.1016/j.apenergy.2017.07.082
[13]	TANG Xiao-lin, YANG Wei, HU Xiao-song, et al. A novel simplified model for torsional vibration analysis of a series-parallel hybrid electric vehicle[J]. Mechanical Systems and Signal Processing, 2017, 85: 329-338. doi: 10.1016/j.ymssp.2016.08.020
[14]	PETTERSSON M, NIELSEN L. Diesel engine speed control with handling of driveline resonances[J]. Control Engineering Practice, 2003, 11 (3): 319-328. doi: 10.1016/S0967-0661(02)00150-8
[15]	BERRIRI M, CHEVREL P, LEFEBVRE D. Active damping of automotive powertrain oscillations by a partial torque compensator[J]. Control Engineering Practice, 2018, 16 (7): 874-883.
[16]	BAUMANN J, TORKZADEH D D, RAMSTEIN A, et al. Model-based predictive anti-jerk control[J]. Control Engineering Practice, 2006, 14 (3): 259-266. doi: 10.1016/j.conengprac.2005.03.026
[17]	傅洪, 田光宇, 陈红旭, 等. 电机-变速器集成驱动系统扭转振动控制的研究[J]. 汽车工程, 2010, 32 (7): 596-600, 595. https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201007012.htm FU Hong, TIAN Guang-yu, CHEN Hong-xu, et al. A study on the torsional vibration control of motor transmission integrated drive system[J]. Automotive Engineering, 2010, 32 (7): 596-600, 595. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201007012.htm
[18]	CHEN Xing, YUAN Shi-hua, PENG Zeng-xiong. Nonlinear vibration for PMSM used in HEV considering mechanical and magnetic coupling effects[J]. Nonlinear Dynamics, 2015, 80 (1/2): 541-552.
[19]	NIU Xi-ze, QIU Jia-jun. Investigation of torsional instability, bifurcation, and chaos of a generator set[J]. IEEE Transactions on Energy Conversion, 2002, 17 (2): 164-168. doi: 10.1109/TEC.2002.1009463
[20]	李永强, 刘杰. 非线性刚度不平衡转子径向碰摩动力学研究[J]. 应用力学学报, 2005, 22 (3): 475-478. doi: 10.3969/j.issn.1000-4939.2005.03.032 LI Yong-qiang, LIU Jie. Dynamics behavior of nonlinear rigid unbalanced rotor system supported on oil film bearing[J]. Chinese Journal of Applied Mechanics, 2005, 22 (3): 475-478. (in Chinese). doi: 10.3969/j.issn.1000-4939.2005.03.032
[21]	KHAN A A, VYAS N S. Nonlinear bearing stiffness parameter estimation in flexible rotor-bearing systems using Volterra and Wiener approach[J]. Probabilistic Engineering Mechanics, 2001, 16 (2): 137-157. doi: 10.1016/S0266-8920(00)00016-3
[22]	吴光强, 栾文博. 汽车传动系相关NVH问题的动力学研究论述[J]. 机械工程学报, 2013, 49 (24): 108-116. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201324013.htm WU Guang-qiang, LUAN Wen-bo. Review of dynamic research for NVH problems related to automotive driveline[J]. Journal of Mechanical Engineering, 2013, 49 (24): 108-116. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201324013.htm
[23]	张立军, 司杨, 余卓平. 燃料电池轿车动力传动系统非线性动态特性仿真分析[J]. 机械工程学报, 2009, 45 (2): 62-67. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200902014.htm ZHANG Li-jun, SI Yang, YU Zhuo-ping. Numerical investigation into nonlinear dynamical characteristics of fuel cell vehicle powertrain system[J]. Journal of Mechanical Engineering, 2009, 45 (2): 62-67. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200902014.htm
[24]	王骏骋, 何仁. 电动轮轮内主动减振器的非线性模糊最优滑模控制[J]. 汽车工程, 2018, 40 (6): 719-725. https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201806015.htm WANG Jun-cheng, HE Ren. Nonlinear optimal sliding mode fuzzy control for in-wheel active vibration damper of electric wheel[J]. Automotive Engineering, 2018, 40 (6): 719-725. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201806015.htm
[25]	HE Ren, WANG Jun-cheng. Vertical vibration control of an in-wheel motor-driven electric vehicle using an in-wheel active vibration system[J]. Asian Journal of Control, 2018, 22 (2): 1-18.
[26]	TALEBITOOTI R, MOROVATI M. Study on TVD parameters sensitivity of a crankshaft using multiple scale and state space method considering quadratic and cubic non-linearities[J]. Latin American Journal of Solids and Structures, 2014, 11 (14): 2672-2695. doi: 10.1590/S1679-78252014001400007
[27]	HARIS A, MOTATO E, THEODOSSIADES S, et al. A study on torsional vibration attenuation in automotive drivetrains using absorbers with smooth and non-smooth nonlinearities[J]. Applied Mathematical Modelling, 2017, 46: 674-690.
[28]	PETTERSSON M, NIELSEN L. Diesel engine speed control with handling of driveline resonances[J]. Control Engineering Practice, 2003, 11 (3): 319-328.
[29]	NAUS G J L, BEENAKKERS M A, HUISMAN R G M, et al. Robust control of a clutch system to prevent judder-induced driveline oscillations[J]. Vehicle System Dynamics, 2010, 48 (11): 1379-1394.
[30]	MASHADI B, BADRYKOOHI M. Driveline oscillation control by using a dry clutch system[J]. Applied Mathematical Modelling, 2015, 39 (21): 6471-6490. doi: 10.1016/j.apm.2015.01.061
[31]	HAN Qing-zhen, HE Ren. Torsional dynamics and stability of automotive driveline considering cubic nonlinearity[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2018, DOI: 10.117/0954407018779655.