Influence of roll and pitch on multipath effect of shipborne GNSS signal
Article Text (Baidu Translation)
-
摘要: 建立了舰船相关坐标系与舰载GNSS天线相关坐标系, 构建了GNSS卫星与倾斜天线的空间位置关系模型; 基于理论分析与动、静态试验, 给出了舰船摇摆条件下GNSS信号的多路径效应随接收机天线倾斜角的变化规律。研究结果表明: 当舰载天线受横纵摇影响连续处于摇晃倾斜姿态时, 卫星信号多路径效应的变化与天线倾斜方向、天线倾角和卫星相对高度角的差有关; 卫星位于天线倾斜方向时, 相对高度角大于天线倾角的卫星信号多路径效应不受天线姿态变化的影响, 小于天线倾角的卫星信号多路径效应随天线倾角的增大而增大, 且逐渐趋于稳定; 卫星位于背对天线倾斜方向时, 相对高度角大于天线倾角的卫星信号多路径效应随天线倾角增大而缓慢增大, 小于天线倾角的卫星信号多路径效应随天线倾角增大而显著增大, 甚至部分卫星信号完全失锁; 卫星处于倾斜天线天顶方位时, 其多路径效应不受天线倾斜角影响。可见, 根据舰船不同姿态确定各颗GNSS观测卫星信号置信度, 可为海上动态精密定位与测量的误差修正问题提供解决方向。Abstract: The ship related coordinate system and ship-based GNSS antenna correlation coordinate system were established, and the spatial position relationship model between the GNSS satellite and tilt antenna was constructed. Based on theoretical analysis and dynamic and static experiments, the variation rules of multipath effect of GNSS signal with the tilt angle of receiver antenna under ship swing condition were given. Analysis result shows that when the ship-based antenna is continuously at the swaying and tilting position by the roll and pitch effect, the variation of multipath effect of satellite signal is related to the antenna tilt direction, antenna tilt angle and the difference of satellite relative height angle. When the satellite faces the antenna tilted direction, the multipath effect of satellite signal with a relative height angle greater than the antenna tilt angle is not affected by the antenna attitude change. The multipath effect of satellite signal with a relative height angle smaller than the antenna tilt angle increases as the antenna tilt angle increases, and gradually becomes stable. When the satellite is in the opposite tilted direction of antenna, the multipath effect of satellite signal whose relative height angle is greater than the antenna tilt angle increases slowly with the increase of antenna tilt angle. While the multipath effect of satellite signal whose relative height angle is smaller than the antenna tilt angle increases significantly with the increase of antenna tilt angle, and even some satellite signals are completely unlocked. When the satellite is at the zenith position of inclined antenna, its multipath effect is not affected by the antenna tilt angle. Therefore, determining the signal confidence of each GNSS observation satellite according to the different attitudes of the ship can provide a solution for the error correction problem of dynamic precision positioning and measurement at sea.
-
图 7 位于天线倾斜方向的卫星多路径效应偏差角度序列
Figure 7. Deviation angle series of multipath effects of satellites facing antenna tilt direction
图 8 xR > 0且E-γ < 0时试验站D观测卫星的多路径效应综合指标
Figure 8. Multipath effect composite indicators of observation satellites at test station D when xR > 0 and E-γ < 0
图 9 位于背对天线倾斜方向的卫星多路径效应偏差角度序列
Figure 9. Deviation angle series of multipath effects of satellites in tilt back azimuth of antenna
图 10 xR < 0且E-γ < 0时试验站D观测卫星的多路径效应综合指标
Figure 10. Multipath effect composite indicators of observation satellites of test station D when xR < 0 and E-γ < 0
图 11 轨迹穿过yRORzR面的卫星多路径效应偏差角度序列
Figure 11. Deviation angle series of multipath effects of satellites passing through plane yRORzR
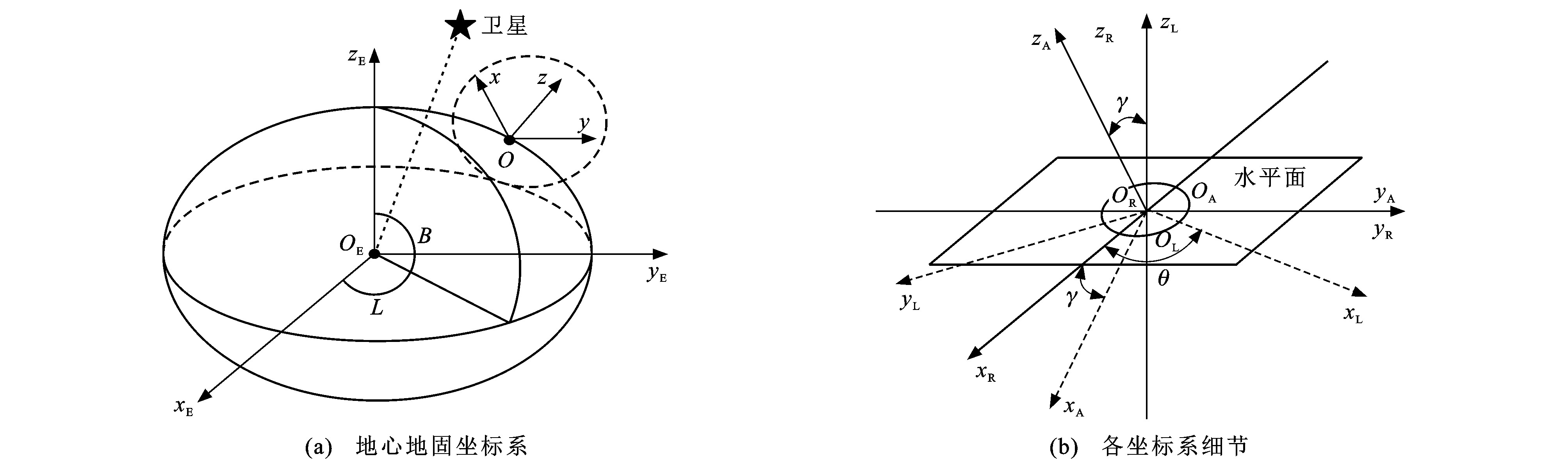
表 1 相关坐标系框架
Table 1. Frameworks of relevant coordinate systems
坐标框架 坐标原点 z轴 x轴 y轴 接收机天线坐标系OAxAyAzA 天线几何中心(OA) 沿天线垂直对称轴指向天顶方向(zA) 与z轴垂直指向天线倾斜方向(xA) 与x轴、z轴构成右手坐标系(yA) 接收机天线水平坐标系ORxRyRzR 天线几何中心(OR) 垂直于水平面指向天顶方向(zR) OAxAyAzA坐标系的xA轴在水平面上的投影(xR) 与x轴、z轴构成右手坐标系(yR) 站心坐标系OLxLyLzL 天线几何中心(OL) 垂直于水平面指向天顶方向(zL) 与z轴垂直指向北极(xL) 与x轴、z轴构成左手坐标系(yL) 地心地固坐标系OExEyEzE 地球质心(OE) 指向国际地球自转服务系统定义的参考极方向(zE) 指向国际地球自转服务系统定义的参考子午面和赤道的交点(xE) 与x轴、z轴构成右手坐标系(yE) 大地坐标系 坐标用纬度B、经度L和大地高程H表示 
下载: 导出CSV
表 2 倾斜天线与卫星的相对位置对信号的影响
Table 2. Effects of relative position of tilted antenna and satellite on signal
倾斜天线与卫星的相对位置 对信号的影响 相对方位 相对高度角 直射信号 多路径信号 xR > 0 E-γ > 0 正常接收 扼流圈削弱 E-γ < 0 正常接收 正常接收 xR≤0 E-γ > 0 正常接收 扼流圈削弱 E-γ < 0 扼流圈削弱 扼流圈削弱
下载: 导出CSV
表 3 试验参数
Table 3. Experimental parameters
接收机型号 中海达iRTK2 采样间隔/s 1 截止高度角/ (°) 15 天线方位角/ (°) 125 天线倾角范围/ (°) 0~70 天线倾角间隔/ (°) 10 卫星信号 GPS、BDS、GLONASS 观测历元 每个倾角观测历元为300个
下载: 导出CSV
-
[1] TABIBI S, GEREMIA-NIEVINSKI F, DAM T V. Statistical comparison and combination of GPS, GLONASS, and multi-GNSS multipath reflectometry applied to snow depth retrieval[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55 (7): 3773-3785. doi: 10.1109/TGRS.2017.2679899 [2] 周红进, 钟云海, 李伟. 大型舰船编队相对导航方法比较[J]. 交通运输工程学报, 2016, 16 (1): 149-158. doi: 10.3969/j.issn.1671-1637.2016.01.018ZHOU Hong-jin, ZHONG Yun-hai, LI Wei. Comparison of relative navigation methods for large vessel formation[J]. Journal of Traffic and Transportation Engineering, 2016, 16 (1): 149-158. (in Chinese). doi: 10.3969/j.issn.1671-1637.2016.01.018 [3] ZHUANG W, TRANQUILLA J M. Effects of multipath and antenna on GPS observables[J]. IEE Proceedings: Radar, Sonar and Navigation, 1995, 142 (5): 267-275. doi: 10.1049/ip-rsn:19951998 [4] 栾锡武, 鲁银涛, 徐涛. 海洋地球物理测量中GPS数据问题与处理[J]. 地球物理学进展, 2005, 20 (4): 897-904. doi: 10.3969/j.issn.1004-2903.2005.04.003LUAN Xi-wu, LU Yin-tao, XU Tao. GPS data problems and its processing in marine geophysical survey[J]. Progress in Geophysics, 2005, 20 (4): 897-904. (in Chinese). doi: 10.3969/j.issn.1004-2903.2005.04.003 [5] SHOJI Y, SATO K, YABUKI M, et al. PWV retrieval over the ocean using shipborne GNSS receivers with MADOCA real-time orbits[J]. Sola, 2016, 12: 265-271. doi: 10.2151/sola.2016-052 [6] 刘永义, 党亚民, 薛树强. 基于海面环境多路径效应建模初探[J]. 测绘科学, 2013, 38 (1): 122-124. https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201301040.htmLIU Yong-yi, DANG Ya-min, XUE Shu-qiang. Preliminary discussion of multipath effect model on sea surface[J]. Science of Surveying and Mapping, 2013, 38 (1): 122-124. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201301040.htm [7] PADROS N, ORTIGOSA J I, BAKER J, et al. Comparative study of high-performance GPS receiving antenna designs[C]//IEEE. Proceedings of the 1996 AP-S International Symposium and URSI Radio Science Meeting. New York: IEEE, 1996: 1958-1961. [8] 范晓燕, 周乾. GPS测量中多路径效应研究综述[J]. 工程地球物理学报, 2010, 7 (3): 382-386. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDQ201003025.htmFAN Xiao-yan, ZHOU Qian. Review of multipath effects in GPS measurement[J]. Chinese Journal of Engineering Geophysics, 2010, 7 (3): 382-386. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCDQ201003025.htm [9] GEORGIADOU Y, KLEUSBERG A. On carrier signal multipath effects in relative GPS positioning[J]. Manuscripta Geodaetica, 1998, 13: 172-179. [10] VAN NEE R D J. Multipath effects on GPS code phase measurements[J]. Navigation: Journal of the Institute of Navigation, 1992, 39 (2): 177-190. doi: 10.1002/j.2161-4296.1992.tb01873.x [11] VAN NEE R D J. Spread-spectrum code and carrier synchronization errors caused by multipath and interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29 (4): 1359-1365. doi: 10.1109/7.259541 [12] 张秀凤, 尹勇, 金一丞. 规则波中船舶运动六自由度数学模型[J]. 交通运输工程学报, 2007, 7 (3): 40-43. doi: 10.3321/j.issn:1671-1637.2007.03.009ZHANG Xiu-feng, YIN Yong, JIN Yi-cheng. Ship motion mathematical model with six degrees of freedom in regular wave[J]. Journal of Traffic and Transportation Engineering, 2007, 7 (3): 40-43. (in Chinese). doi: 10.3321/j.issn:1671-1637.2007.03.009 [13] LAU L, CROSS P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling[J]. Journal of Geodesy, 2007, 81: 713-732. doi: 10.1007/s00190-007-0139-z [14] GE L, CHEN H Y, HAN S, et al. Adaptive filtering of continuous GPS results[J]. Journal of Geodesy, 2000, 74: 572-580. doi: 10.1007/s001900000120 [15] ZHONG P, DING X L, ZHENG D W, et al. Adaptive wavelet transform based on cross-validation method and its application to GPS multipath mitigation[J]. GPS Solutions, 2008, 12 (2): 109-117. doi: 10.1007/s10291-007-0071-y [16] 张志伟, 暴景阳, 肖付民, 等. 多波束测点位置归算横纵摇耦合效应分析[J]. 地理与地理信息科学, 2016, 32 (4): 38-41. doi: 10.3969/j.issn.1672-0504.2016.04.007ZHANG Zhi-wei, BAO Jing-yang, XIAO Fu-min, et al. Pitch-rolling coupling effect analysis on position reduction of multibeam echosounder[J]. Geography and Geo-Information Science, 2016, 32 (4): 38-41. (in Chinese). doi: 10.3969/j.issn.1672-0504.2016.04.007 [17] 魏玉阔. 多波束测深假象消除与动态空间归位技术[D]. 哈尔滨: 哈尔滨工程大学, 2011.WEI Yu-kuo. Technique of bathymetric artifact elimination and seafloor footprint positioning for multibeam bathymetry[D]. Harbin: Harbin Engineering University, 2011. (in Chinese). [18] HARE R. Depth and position error budgets for multibeam echosounding[J]. International Hydrographic Review, 2015, 72 (2): 37-69. [19] BJ∅RKE J T. Computation of calibration parameters for multibeam echo sounders using the least squares method[J]. IEEE Journal of Oceanic Engineering, 2005, 30 (4): 818-831. doi: 10.1109/JOE.2005.862138 [20] 郭海林, 陈亮. 利用MP提高GPS单点定位精度的研究[J]. 测绘通报, 2016 (3): 25-28. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201603009.htmGUO Hai-lin, CHEN Liang. Research on improving GPS point positioning precision by MP[J]. Bulletin of Surveying and Mapping, 2016 (3): 25-28. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201603009.htm [21] AGTERBERG F P. Combining indicator patterns in weights of evidence modeling for resource evaluation[J]. Nonrenewable Resources, 1992, 1 (1): 39-50. doi: 10.1007/BF01782111 [22] 李国伟, 郭金运, 原永东, 等. GPS测站多路径效应建模研究[J]. 测绘科学, 2013, 38 (3): 7-9, 21. https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201303003.htmLI Guo-wei, GUO Jin-yun, YUAN Yong-dong, et al. Studies of modeling multipath effect at GPS station[J]. Science of Surveying and Mapping, 2013, 38 (3): 7-9, 21. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201303003.htm [23] LUO Yu, WANG Yong-qing, WU Si-liang, et al. Multipath effects on vector tracking algorithm for GNSS signal[J]. Science China (Information Sciences), 2014, 57 (10): 145-157. [24] 李晓光, 程鹏飞, 成英燕, 等. GNSS数据质量分析[J]. 测绘通报, 2017 (3): 1-4, 8. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201703001.htmLI Xiao-guang, CHENG Peng-fei, CHENG Ying-yan, et al. Quality analysis of GNSS data[J]. Bulletin of Surveying and Mapping, 2017 (3): 1-4, 8. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201703001.htm [25] STRODE P R R, GROVES P D. GNSS multipath detection using three-frequency signal-to-noise measurements[J]. GPS Solutions, 2016, 20 (3): 399-412. doi: 10.1007/s10291-015-0449-1 [26] 唐龙江, 徐爱功, 徐宗秋, 等. 复杂环境下多模GNSS接收机性能评估[J]. 导航定位学报, 2017, 5 (4): 105-109. https://www.cnki.com.cn/Article/CJFDTOTAL-CHWZ201704019.htmTANG Long-jiang, XU Ai-gong, XU Zong-qiu, et al. Performance evaluation of multimode GNSS receiver for CORS network[J]. Journal of Navigation and Positioning, 2017, 5 (4): 105-109. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHWZ201704019.htm [27] 田宗彪, 章磊, 张训虎, 等. GNSS点位质量评定中多路径效应分析研究[J]. 工程勘察, 2017 (2): 45-48. https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC201702009.htmTIAN Zong-biao, ZHANG Lei, ZHANG Xun-hu, et al. Study of multipath effects in GNSS points quality assessment[J]. Geotechnical Investigation and Surveying, 2017 (2): 45-48. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCKC201702009.htm [28] 周冬梅. 基于小波变换的多路径误差研究[D]. 赣州: 江西理工大学, 2010.ZHOU Dong-mei. Research on multipath error based on wavelet transform[D]. Ganzhou: Jiangxi University of Science and Technology, 2010. (in Chinese). [29] YI Ting-hua, LI Hong-nan, GU Ming. Effect of different construction materials on propagation of GPS monitoring signals[J]. Measurement: Journal of the International Measurement Confederation, 2012, 45 (5): 1126-1139. doi: 10.1016/j.measurement.2012.01.027 [30] FAN K K, DING X L. Estimation of GPS carrier phase multipath signals based on site environment[J]. Journal of Global Positioning Systems, 2006, 5 (1): 22-28. [31] 薛志宏. GNSS动态变形测量关键技术研究[D]. 郑州: 解放军信息工程大学, 2012.XUE Zhi-hong. A study of key technology for dynamic deformation monitoring using GNSS[D]. Zhengzhou: PLA Information Engineering University, 2012. (in Chinese). -
点击查看大图
图(11) / 表(3)
计量
- 文章访问数: 849
- HTML全文浏览量: 144
- PDF下载量: 272
- 被引次数: 0
