Heterogeneous vehicular network selection method considering network congestion and system fairness
-
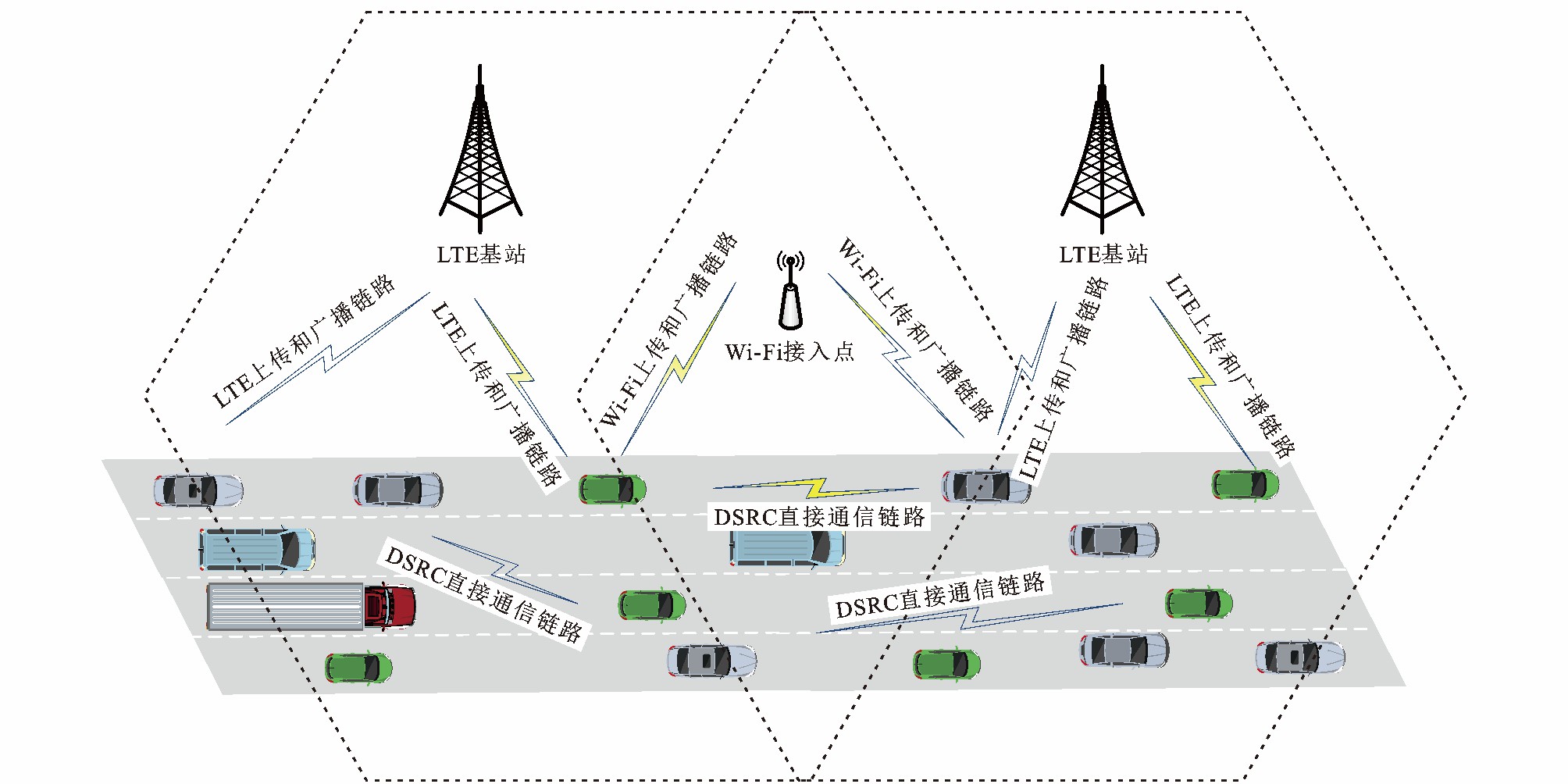
摘要: 利用演化博弈的有限理智特性执行网络选择, 以实现车载异构网络系统中网络资源的均衡分配; 利用双层博弈对演化博弈方法进行优化, 保证极端拥堵中部分车辆消息传输的同时, 维持系统公平; 设计了专用短程通信、长期演进和无线局域网融合的车载异构网络仿真场景, 对比了基于多准则决策的传统方法、基于演化博弈的网络选择方法和基于双层博弈的网络选择方法。仿真结果表明: 采用基于演化博弈和双层博弈的车载异构网络选择方法首次解决了动态网络环境中车载异构网络切换时出现的大规模乒乓效应, 利用双层博弈能够实现拥堵抑制和系统公平; 采用基于双层博弈的网络选择方法能够驱动异构网络系统在2~3个切换周期内实现网络系统状态的稳定; 在预设的动态网络评价条件下与80个终端的一般场景中, 双层博弈终端平均网络评价指标高于演化博弈19.5%, 为3种网络协同工作提供可靠服务; 在190个终端极端拥堵场景中, 终端合理分配, 共享专用短程通信网络资源, 双层博弈终端平均网络评价指标高于演化博弈10.3%, 双层博弈专用短程通信网络评价指标为演化博弈的2.18倍, 可以保证车联网基本安全信息的广播、系统的公平并维系基本车联网服务。Abstract: The bounded rationality characteristic of evolutionary game was used to implement the network selection, and the network resource of heterogeneous vehicular network system was evenly distributed. The fairness of the system was guaranteed by optimizing evolutionary game with two-layer game while some of the vehicles can transmit message in extreme congestion. The network simulation scene combined with dedicated short-range communication (DSRC), long-term evolution, and wireless local area network was designed, and the traditional method based on multiple criteria decision making, the network selection method based on evolutionary game, and the network selection method based on two-layer game were compared. Simulation result shows that the large scale ping-pong effects of dynamic network environment in heterogeneous vehicular network switching was firstly solved by using the heterogeneous vehicular network selection method based on evolutionary game and two-layer game. The two-layer game can suppress congestion and provide system fairness. The network selection method based on two-layer game can drive the heterogeneous network system to achieve the stability of network system state in 2-3 switching cycles. In the preset dynamic network evaluation condition and the general scene with 80 terminals, the terminal average network evaluation index of two-layer game is 19.5% higher than that of evolutionary game, and it provides reliable services for three kinds of network cooperation. In the extreme congestion scenario with 190 terminals, the terminals are reasonably distributed and share the DSRC network resources. The terminal average network evaluation index of two-layer game is 10.3% higher than that of evolutionary game, and the evaluation index of two-layer game DSRC network is 2.18 times of evolutionary game. Therefore, the basic safety messages broadcast, system fairness and basic connected vehicle service can be ensured.
-
图 1 车载异构网络系统拓扑结构
Figure 1. Topological structure of heterogeneous vehicular network system
图 2 终端数量与网络评价指标的关系
Figure 2. Relationship between terminal number and network evaluation index
图 4 基于演化博弈的网络选择方法流程
Figure 4. Flow of network selection method based on evolutionary game
图 5 基于演化博弈的网络选择方法仿真结果
Figure 5. Simulation results of network selection method based on evolutionary game
图 6 基于多准则决策的网络选择方法仿真结果
Figure 6. Simulation results of network selection method based on MCDM
图 7 演化博弈和MCDM方法终端平均网络评价指标
Figure 7. Terminal average network evaluation indexes between evolutionary game and MCDM method
图 9 一般场景下基于演化博弈的网络选择方法仿真结果
Figure 9. Simulation results of network selection method based on evolutionary game in regular scenario
图 10 一般场景下基于双层博弈的网络选择方法仿真结果
Figure 10. Simulation results of network selection method based on two-layer game in regular scenario
图 11 一般场景下双层博弈和演化博弈终端平均网络评价指标
Figure 11. Average network evaluation indexes between two-layer game and evolutionary game in regular scenario
图 12 拥堵场景下基于演化博弈的网络选择方法仿真结果
Figure 12. Simulation results of network selection method based on evolutionary game in congestion scenario
图 13 拥堵场景下基于双层博弈的网络选择方法仿真结果
Figure 13. Simulation results of network selection method based on two-layer game in congestion scenario
图 14 拥堵场景下双层博弈和演化博弈终端平均网络评价指标
Figure 14. Average network evaluation indexes between two-layer game and evolutionary game in congestion scenario
图 15 拥堵场景下双层博弈和演化博弈方法公平性对比
Figure 15. Equality comparison between two-layer game and evolutionary game in congestion scenario
图 17 随机性能场景下基于双层博弈的终端数量
Figure 17. Fig. 17 Terminal numbers based on two-layer game in random-performance scenario
-
[1] 赵祥模, 惠飞, 史昕, 等. 泛在交通信息服务系统的概念、架构与关键技术[J]. 交通运输工程学报, 2014, 14 (4): 105-115. http://transport.chd.edu.cn/article/id/201404013ZHAO Xiang-mo, HUI Fei, SHI Xin, et al. Concept, architecture and challenging technologies of ubiquitous traffic information service system[J]. Journal of Traffic and Transportation Engineering, 2014, 14 (4): 105-115. (in Chinese). http://transport.chd.edu.cn/article/id/201404013 [2] KENNEY J B. Dedicated short-range communications (DSRC) standards in the United States[J]. Proceedings of the IEEE, 2011, 99 (7): 1162-1182. doi: 10.1109/JPROC.2011.2132790 [3] XU Zhi-gang, LI Xiao-chi, ZHAO Xiang-mo, et al. DSRC versus 4G-LTE for connected vehicle applications: a study on field experiments of vehicular communication performance[J]. Journal of Advanced Transportation, 2017, 2017: 1-10. [4] SU K C, WU H M, CHANG W L, et al. Vehicle-to-vehicle communication system through Wi-Fi network using android smartphone[C]//IEEE. 2012 International Conference on Connected Vehicles and Expo (ICCVE). New York: IEEE, 2013: 191-196. [5] HOSSAIN E, CHOW G, LEUNG V C M, et al. Vehicular telematics over heterogeneous wireless networks: a survey[J]. Computer Communications, 2010, 33 (7): 775-793. doi: 10.1016/j.comcom.2009.12.010 [6] YLIANTTILA M, PANDE M, MÄKELÄ J, et al. Optimization scheme for mobile users performing vertical handoffs between IEEE 802.11 and GPRS/EDGE networks[C]//IEEE. IEEE Global Telecommunications Conference. New York: IEEE, 2001: 3439-3443. [7] BUDDHIKOT M, CHANDRANMENON G, HAN S, et al. Integration of 802.11 and third-generation wireless data networks[C]//IEEE. The Conference on Computer Communications—22nd Annual Joint Conference of the IEEE Computer and Communications Societies. New York: IEEE, 2003: 503-512. [8] HAIDER A, GONDAL I, KAMRUZZAMAN J. Dynamic dwell timer for hybrid vertical handover in 4G coupled networks[C]//IEEE. 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring). New York: IEEE, 2011: 1-5. [9] NIYATO D, HOSSAIN E. Dynamics of network selection in heterogeneous wireless networks: an evolutionary game approach[J]. IEEE Transactions on Vehicular Technology, 2009, 58 (4): 2008-2017. doi: 10.1109/TVT.2008.2004588 [10] MA Dong, MA Mao-de. A QoS-based vertical handoff scheme for interworking of WLAN and WiMAX[C]//IEEE. GLOBECOM—IEEE Global Telecommunications Conference. New York: IEEE, 2009: 1-6. [11] SEPULCRE M, GOZALVEZ J, ALTINTAS O, et al. Context-aware heterogeneous V2I communications[C]//IEEE. 7th International Workshop on Reliable Networks Design and Modeling. New York: IEEE, 2015: 295-300. [12] TIAN Da-xin, ZHOU Jian-shan, WANG Yun-peng, et al. A dynamic and self-adaptive network selection method for multimode communications in heterogeneous vehicular telematics[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16 (6): 3033-3049. doi: 10.1109/TITS.2015.2422144 [13] MARQUEZ-BARJA J M, AHMADI H, TORNELL S M, et al. Breaking the vehicular wireless communications barriers: vertical handover techniques for heterogeneous networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64 (12): 5878-5890. doi: 10.1109/TVT.2014.2386911 [14] WANG Shang-guang, FAN Cun-qun, HSU Ching-hsien, et al. A vertical handoff method via self-selection decision tree for internet of vehicles[J]. IEEE Systems Journal, 2016, 10 (3): 1183-1192. doi: 10.1109/JSYST.2014.2306210 [15] AWAD A, MOHAMED A, CHIASSERINI C F. Dynamic network selection in heterogeneous wireless networks: a user-centric scheme for improved delivery[J]. IEEE Consumer Electronics Magazine, 2017, 6 (1): 53-60. doi: 10.1109/MCE.2016.2614419 [16] KIM S. Fog radio access network system control scheme based on the embedded game model[J]. Eurasip Journal on Wireless Communications and Networking, 2017, 2017 (1): 1-5. doi: 10.1186/s13638-016-0795-x [17] AGRAWAL S, TYAGI N, MISRA A K. Seamless VANET connectivity through heterogeneous wireless network on rural highways[C]//ACM. 2nd International Conference on Information and Communication Technology for Competitive Strategies. New York: ACM, 2016: 1-5. [18] DEY K C, RAYAMAJHI A, CHOWDHURY M, et al. Vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communication in a heterogeneous wireless network—performance evaluation[J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 168-184. doi: 10.1016/j.trc.2016.03.008 [19] SYFULLAH M, LIMJ M Y. Data broadcasting on Cloud-VANET for IEEE 802.11p and LTE hybrid VANET architectures[C]//IEEE. 3rd IEEE International Conference on Computational Intelligence and Communication Technology. New York: IEEE, 2017: 1-6. [20] CHARITOS M, KALIVAS G. MIMO HetNet IEEE 802.11p-LTE deployment in a vehicular urban environment[J]. Vehicular Communications, 2017, 9: 222-232. doi: 10.1016/j.vehcom.2016.12.004 [21] SALVO P, TURCANU I, CUOMO F, et al. Heterogeneous cellular and DSRC networking for floating car data collection in urban areas[J]. Vehicular Communications, 2017, 8: 21-34. [22] CHANG C J, TSAI T L, CHEN Y H. Utility and game-theory based network selection scheme in heterogeneous wireless networks[C]//IEEE. 2009 IEEE Wireless Communications and Networking Conference. New York: IEEE, 2009: 2846-2850. [23] ZHU Kun, NIYATO D, WANG Ping. Network selection in heterogeneous wireless networks: evolution with incomplete information[C]//IEEE. IEEE Wireless Communications and Networking Conference. New York: IEEE, 2010: 1-6. [24] PERVAIZ H, MEI Hai-bo, BIGHAM J, et al. Enhanced cooperation in heterogeneous wireless networks using coverage adjustment[C]//ACM. 6th International Wireless Communications and Mobile Computing Conference. New York: ACM, 2010: 241-245. [25] LIU Xing-wei, FANG Xu-ming, CHEN Xu, et al. A bidding model and cooperative game-based vertical handoff decision algorithm[J]. Journal of Network and Computer Applications, 2011, 34 (4): 1263-1271. doi: 10.1016/j.jnca.2011.01.012 [26] LIU Bin, TIAN Hui, WANG Bin, et al. AHP and game theory based approach for network selection in heterogeneous wireless networks[C]//IEEE. 2014 IEEE 11th Consumer Communications and Networking Conference. New York: IEEE, 2014: 501-506. [27] CAMPOLO C, VINEL A, MOLINARO A, et al. Modeling broadcasting in IEEE 802.11p/WAVE vehicular networks[J]. IEEE Communications letters, 2011, 15 (2): 199-201. [28] VINEL A. 3GPP LTE versus IEEE 802.11p/WAVE: which technology is able to support cooperative vehicular safety applications?[J]. IEEE Wireless Communications Letters, 2012, 1 (2): 125-128. [29] BALDO N, REQUENA-ESTESO M, NÚÑEZ-MARTÍNEZ J, et al. Validation of the IEEE 802.11 MAC model in the ns3 simulator using the EXTREME testbed[C]//ICST. 3rd International ICST Conference on Simulation Tools and Techniques. Bratislava: ICST, 2010: 1-9. [30] HOFBAUER J, SIGMUND K. Evolutionary game dynamics[R]. Laxenburg: IIASA, 2003. [31] BAZZI A, MASINI B M, ZANELLA A, et al. On the performance of IEEE 802.11p and LTE-V2V for the cooperative awareness of connected vehicles[J]. IEEE Transactions on Vehicular Technology, 2017, 66 (11): 10419-10432. -
下载:
点击查看大图
计量
- 文章访问数: 609
- HTML全文浏览量: 112
- PDF下载量: 372
- 被引次数: 0
