Nonlinear dynamics characteristics of maglev vehicle under track random irregularities
-
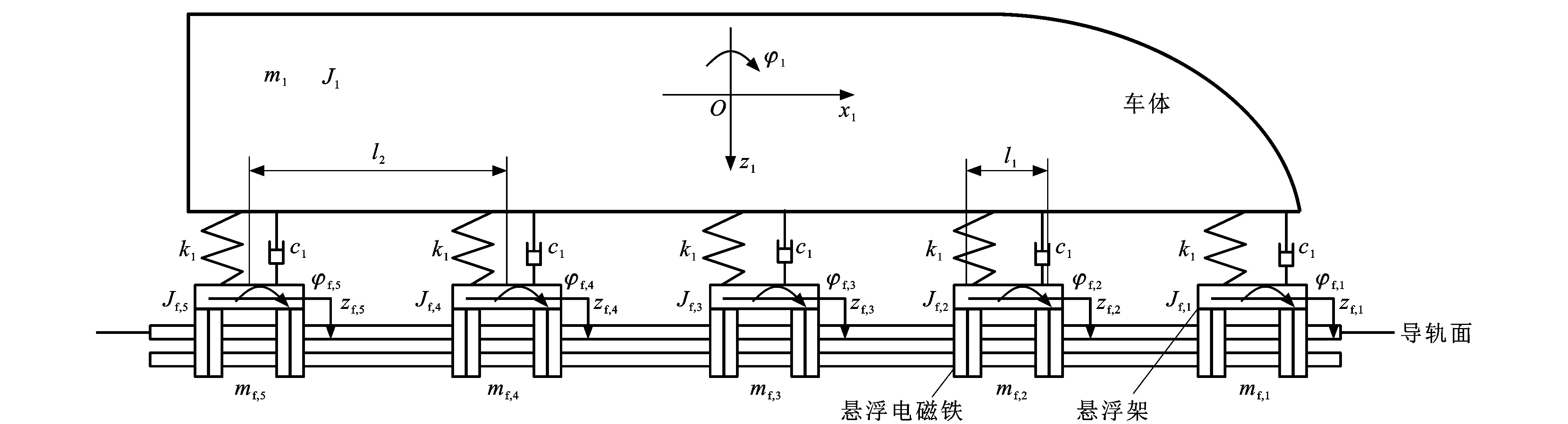
摘要: 基于柔性轨道研究了随机不平顺下磁浮车辆的动力学特性, 在将轨道受力分解为分段链式结构的基础上, 提出了一种磁浮车辆垂向悬浮稳定性分析方法, 定义了不同悬浮力作用于各自悬浮点时柔性轨道的振动固有频率和模态矩阵; 建立了轨道分段链式结构的离散形式和轨道结构的运动方程, 采用虚拟激励法将轨道不平顺产生的随机激励转化为系统输入激励, 并将轨道随机高低不平顺作为振动激励源进行车轨振动控制; 在不同反馈控制参数下采用电压反馈双环PID控制器数值仿真车辆的悬浮状态, 并分析了轨道随机不平顺激励下反馈控制参数对磁浮系统稳定性的影响。研究结果表明: 当磁浮车辆速度为50~80 km·h-1, 位移反馈参数、速度反馈参数和电流反馈参数分别为140 000、50、500时, 车辆可以从起始间隙16 mm快速定位到平衡位置间隙9 mm, 在2.2 s时即可稳定悬浮, 系统的超调量和稳态误差分别为1.50和0.13 mm, 且系统振动频率趋近于0;当位移反馈参数、速度反馈参数和电流反馈参数分别为15 000、50、400时, 磁浮车辆在轨道随机不平顺作用下的悬浮稳定性变差, 系统在9 s左右逐渐趋于稳定, 但仍旧在平衡位置上下浮动, 且系统振动频率和振动幅值分别为7 Hz和0.5 mm; 当磁浮车辆的速度超出50~80 km·h-1时, 第1组反馈控制参数不再适用, 磁浮系统在1.7 s左右发散, 车辆失稳, 表明在不同车辆速度和反馈控制参数的作用下, 轨道随机不平顺能显著影响磁浮车辆的悬浮稳定性。Abstract: The dynamics characteristics of maglev vehicle caused by the random irregularity were studied based on the flexible track. Based on decomposing the track force into a segmented chain structure, an analysis method for the vertical suspension stability of maglev vehicle was proposed. The vibration natural frequencies and modal matrices of flexible track were defined when different suspension forces acted on their respective suspension points. The discrete form of track segmented chain structure and the motion equation of track structure were established. The random excitation generated by the track irregularity was transformed to the system input excitation by the virtual excitation method, and the vibrations of vehicle and track were controlled by taking the random unevenness irregularity of track as the vibration excitation source. The double-loop PID controller with the voltage feedback was used to numerically simulate the vehicle suspension state under different feedback control parameters, and the influences of feedback control parameters on the maglev system stability under the random track irregularity excitation were analyzed. Research result shows that when the maglev vehicle speed is 50-80 km·h-1 and the displacement feedback parameter, speed feedback parameter and current feedback parameter are 140 000, 50 and 500, respectively, the vehicle can quickly locate from the initial gap of 16 mm to the equilibrium position (9 mm), and can achieve a stable suspension at 2.2 s. The overshoot and steady-state error of system are-1.50 and 0.13 mm, respectively, and the vibration frequency approaches zero. When the displacement feedback parameter, speed feedback parameter and current feedback parameter are 15 000, 50 and 400, respectively, the maglev vehicle suspension stability becomes worse under the action of track random irregularity. The system tends to be stable gradually around 9 s, but it still floats up and down at the equilibrium position, and the vibration frequency and amplitude of system are 7 Hz and 0.5 mm, respectively. When the maglev vehicle speed exceeds 50-80 km·h-1, the first set of feedback control parameters are no longer applicable. The maglev system diverges around 1.7 s, and the train is unstable, indicating that under the actions of different vehicle speeds and feedback control parameters, the track random irregularity can significantly affect the suspension stability of maglev vehicle.
-
图 4 不同反馈控制参数下悬浮间隙曲线
Figure 4. Suspension gap curves under different feedback control parameters
图 5 不同反馈控制参数下控制电流曲线
Figure 5. Control current curves under different feedback control parameters
图 6 不恰当反馈控制参数下悬浮间隙发散曲线
Figure 6. Suspension gap divergence curve under unsuitable feedback control parameters
图 7 不恰当反馈控制参数下控制电流发散曲线
Figure 7. Control current divergent curve under unsuitable feedback control parameters
表 1 车轨耦合系统物理参数
Table 1. Physical parameters of vehicle track coupling system
物理参数 参数值 车体质量/t 25 悬浮架质量/kg 750 每延米轨道质量/kg 8 937.755 线圈匝数 700 目标气隙/m 0.009 电磁铁面积/m2 0.024 真空磁导率/ (H·m-1) 4π×10-7 线圈电阻/Ω 1.2 稳定电流/A 19.5 漏磁率 0 
下载: 导出CSV
-
[1] 郑浩哲. 随机路面行驶车辆振动响应的快速虚拟激励算法[J]. 汽车工程, 1993, 15 (5): 268-275. https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC199305002.htmZHENG Hao-zhe. A fast computing method for random vibrations of road vehicles[J]. Automotive Engineering, 1993, 15 (5): 268-275. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC199305002.htm [2] 赵又群, 郭孔辉. 具有随机道路输入的人-车-路闭环操纵系统的响应分析与操纵安全性评价[J]. 汽车工程, 1997, 19 (5): 273-278. doi: 10.3321/j.issn:1000-680X.1997.05.001ZHAO You-qun, GUO Kong-hui. Response analysis and handing safety evaluation for driver/vehicle/road closed-loop maneuvering system with random road input[J]. Automotive Engineering, 1997, 19 (5): 273-278. (in Chinese). doi: 10.3321/j.issn:1000-680X.1997.05.001 [3] 李强, 周济. 重型越野车的非平稳随机激励系统优化设计方法[J]. 机械强度, 1998, 20 (1): 45-52. https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD801.010.htmLI Qiang, ZHOU Ji. The dynamic optimization design method of nonstationary stochastic excitation heavy truck[J]. Journal of Mechanical Strength, 1998, 20 (1): 45-52. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD801.010.htm [4] 李杰, 陈建兵. 随机结构动力可靠性分析的概率密度演化方法[J]. 力学学报, 2004, 17 (2): 121-125. doi: 10.3969/j.issn.0258-1825.2004.02.001LI Jie, CHEN Jian-bing. Probability density evolution method for dynamic reliability analysis of stochastic structures[J]. Journal of Vibration Engineering, 2004, 17 (2): 121-125. (in Chinese). doi: 10.3969/j.issn.0258-1825.2004.02.001 [5] 陈建兵, 李杰. 随机荷载作用下随机结构线性反应的概率密度演化分析[J]. 固体力学学报, 2004, 25 (1): 119-124. doi: 10.3969/j.issn.0254-7805.2004.01.025CHEN Jian-bing, LI Jie. Probability density evolution of linear stochastic structural response[J]. Acta Mechanica Solida Sinica, 2004, 25 (1): 119-124. (in Chinese). doi: 10.3969/j.issn.0254-7805.2004.01.025 [6] 李杰, 陈建兵. 随机动力系统中的概率密度演化方程及其研究进展[J]. 力学进展, 2010, 40 (2): 170-188. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201002005.htmLI Jie, CHEN Jian-bing. Advances in the research on probability density evolution equations of stochastic dynamical systems[J]. Advances in Mechanics, 2010, 40 (2): 170-188. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201002005.htm [7] 林家浩, 钟万勰, 张文首. 结构非平稳随机响应方差矩阵的直接精细积分计算[J]. 振动工程学报, 1999, 12 (1): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC901.000.htmLIN Jia-hao, ZHONG Wan-xie, ZHANG Wen-shou. Precise integration of the variance matrix of structural nonstationary random responses[J]. Journal of Vibration Engineering, 1999, 12 (1): 1-8. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC901.000.htm [8] 吕峰. 车辆与结构相互作用随机动力分析[D]. 大连: 大连理工大学, 2008.LYU Feng. Stochastic analysis for dynamic interaction of vehicles and structures[D]. Dalian: Dalian University of Technology, 2008. (in Chinese). [9] 张志超. 车桥系统耦合振动和地震响应的随机分析[D]. 大连: 大连理工大学, 2010.ZHANG Zhi-chao. Stochastic analysis for the coupling vibration and seismic responses of train-bridge systems[D]. Dalian: Dalian University of Technology, 2010. (in Chinese). [10] ZHANG Z C, LIN J H, ZHANG Y H, et al. Non-stationary random vibration analysis of three-dimensional train-bridge systems[J]. Vehicle System Dynamics, 2010, 48 (4): 457-480. doi: 10.1080/00423110902866926 [11] ZHANG Z C, ZHANG Y H, LIN J H, e al. Random vibration of a train traversing a bridge subjected to traveling seismic waves[J]. Engineering Structures, 2011, 33 (12): 3546-3558. doi: 10.1016/j.engstruct.2011.07.018 [12] ZHANG Y W, LIN J H, ZHAO Y, et al. Symplectic random vibration analysis of a vehicle moving on an infinitely long periodic track[J]. Journal of Sound and Vibration, 2010, 329 (21): 4440-4454. doi: 10.1016/j.jsv.2010.05.004 [13] 赵春发, 翟婉明, 王开云. 磁悬浮车辆随机振动响应分析及其平稳性研究[J]. 中国机械工程, 2002, 13 (16): 1402-1407. doi: 10.3321/j.issn:1004-132X.2002.16.016ZHAO Chun-fa, ZHAI Wan-ming, WANG Kai-yun. A study on maglev vehicle vertical random vibration and ride quality[J]. China Mechanical Engineering, 2002, 13 (16): 1402-1407. (in Chinese). doi: 10.3321/j.issn:1004-132X.2002.16.016 [14] MACE B R, MANCONI E. Modelling wave propagation in two-dimensional structures using finite element analysis[J]. Journal of Sound and Vibration, 2008, 318 (4/5): 884-902. [15] 张玲玲. 磁浮列车悬浮系统的Hopf分岔及滑模控制研究[D]. 长沙: 湖南大学, 2010.ZHANG Ling-ling. Research on Hopf bifurcation and sliding mode control for suspension system of maglev train[D]. Changsha: Hunan University, 2010. (in Chinese). [16] XU Jun-qi, CHEN Chen, GAO Ding-gang, et al. Nonlinear dynamic analysis on maglev train system with flexible guideway and double time-delay feedback control[J]. Journal of Vibroengineering, 2017, 19 (8): 6346-6362. doi: 10.21595/jve.2017.18970 [17] 吕峰, 林家浩, 张亚辉. 车辆-轨道系统垂向随机振动的辛方法分析[J]. 力学学报, 2008, 40 (3): 381-387. doi: 10.3321/j.issn:0459-1879.2008.03.012LYU Feng, LIN Jia-hao, ZHANG Ya-hui. Random vibration analysis of vehicle-track coupling systems using symplectic method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40 (3): 381-387. (in Chinese). doi: 10.3321/j.issn:0459-1879.2008.03.012 [18] LYUF, KENNEDYD, WILLIAMSF W, et al. Symplectic analysis of vertical random vibration for coupled vehicle-track systems[J]. Journal of Sound and Vibration, 2008, 317(1/2): 236-249. (in Chinese) [19] MAZILU T, DUMITRIU M, TUDORACHE C. On the dynamics of interaction between a moving mass and an infinite one-dimensional elastic structure at the stability limit[J]. Journal of Sound and Vibration, 2011, 330 (15): 3729-3743. doi: 10.1016/j.jsv.2011.02.026 [20] 张有为. 车辆-轨道耦合系统高效随机振动分析及优化[D]. 大连: 大连理工大学, 2013.ZHANG You-wei. Efficient random vibration analysis and optimization for coupled vehicle-track systems[D]. Dalian: Dalian University of Technology, 2013. (in Chinese). [21] LI Jin-hui, LI Jie, ZHOU Dan-feng, et al. The active control of maglev stationary self-excited vibration with a virtual energy harvester[J]. IEEE Transactions on Industrial Electronics, 2015, 62 (5): 2942-2951. doi: 10.1109/TIE.2014.2364788 [22] 张丽萍, 郭立新. 基于逆虚拟激励法的随机路面谱的识别方法[J]. 东北大学学报(自然科学版), 2012, 33 (2): 258-261. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201202027.htmZHANG Li-ping, GUO Li-xin. Identification of random road spectrum based on inverse pseudo-excitation method[J]. Journal of Northeast University (Natural Science), 2012, 33 (2): 258-261. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201202027.htm [23] 王辉, 钟晓波, 沈钢. 一种新型磁悬浮线路设计方案及悬浮控制方法[J]. 同济大学学报(自然科学版), 2013, 41 (7): 1112-1118. doi: 10.3969/j.issn.0253-374x.2013.07.026WANG Hui, ZHONG Xiao-bo, SHEN Gang. A new maglev line system design and control strategy[J]. Journal of Tongji University (Natural Science), 2013, 41 (7): 1112-1118. (in Chinese). doi: 10.3969/j.issn.0253-374x.2013.07.026 [24] TSUNASHIMA H, ABE M. Static and dynamic performance of permanent magnet suspension for maglev transport vehicle[J]. Vehicle System Dynamics, 1998, 29 (2): 83-111. doi: 10.1080/00423119808969368 [25] CHEN Chen, XU Jun-qi, JI Wen, et. al. Sliding mode robust adaptive control of maglev vehicle's nonlinear suspension system based on flexible track: design and experiment[J]. IEEE Access, 2019, 7: 41874-41884. doi: 10.1109/ACCESS.2019.2906245 [26] SUN You-gang, XU Jun-qi, QIANG Hai-yan, et. al. Adaptive sliding mode control of maglev system based on RBF neural network minimum parameter learning method[J]. Measurement, 2019, 141: 217-226. [27] XU Jun-qi, CHEN Chen, SUN You-gang, et al. Multi point suspension cooperative modeling and control of low speed maglev vehicle[C]//IEEE. 2018 Chinese Automation Congress (CAC 2018). New York: IEEE, 2018: 3317-3322. [28] 张青霞, 段忠东, JANKOWSKI L. 基于虚拟变形法的车-桥耦合系统移动质量识别[J]. 力学学报, 2011, 43 (3): 598-610. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201103021.htmZHANG Qing-xia, DUAN Zhong-dong, JANKOWSKI L. Moving mass identification of vehicle-bridge coupled system based on virtual distortion method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43 (3): 598-610. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201103021.htm [29] 李小珍, 朱艳, 强士中. 车桥系统空间非平稳随机分析[J]. 铁道学报, 2012, 34 (6): 88-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201206021.htmLI Xiao-zhen, ZHU Yan, QIANG Shi-zhong. Spatial train-bridge coupling system non-stationary stochastic responses analysis[J]. Journal of the China Railway Society, 2012, 34 (6): 88-94. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201206021.htm [30] 孙作玉, 王晖. 结构非平稳随机响应方差数值计算方法[J]. 振动工程学报, 2009, 22 (3): 325-328. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200903019.htmSUN Zuo-yu, WANG Hui. Calculation method of the variance matrix of structural non-stationary random responses[J]. Journal of Vibration Engineering, 2009, 22 (3): 325-328. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200903019.htm -
点击查看大图
图(11) / 表(1)
计量
- 文章访问数: 2033
- HTML全文浏览量: 187
- PDF下载量: 1270
- 被引次数: 0
