航路时空资源分配的多目标优化方法

田文; 杨帆; 尹嘉男; 宋津津

doi:10.19818/j.cnki.1671-1637.2020.06.019

航路时空资源分配的多目标优化方法

doi: 10.19818/j.cnki.1671-1637.2020.06.019

南京航空航天大学民航学院, 江苏南京 211106

基金项目:

国家自然科学基金项目 71971112

国家自然科学基金项目 61903187

国家自然科学基金项目 52002178

江苏省自然科学基金项目 BK20190416

江苏省自然科学基金项目 BK20190414

中央高校基本科研业务费专项资金项目 kfjj20190717

详细信息

作者简介:
田文(1981-), 女, 山东青岛人, 南京航空航天大学讲师, 工学博士, 从事空中交通流量管理研究

中图分类号: V355
计量
- 文章访问数: 884
- HTML全文浏览量: 164
- PDF下载量: 255
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-06
- 刊出日期: 2020-06-25

Multi-objective optimization method of air route space-time resources allocation

School of Civial Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, Jiangsu, China

Funds:

National Natural Science Foundation of China 71971112

National Natural Science Foundation of China 61903187

National Natural Science Foundation of China 52002178

Natural Science Foundation of Jiangsu Province BK20190416

Natural Science Foundation of Jiangsu Province BK20190414

Fundamental Research Funds for the Central Universities kfjj20190717

More Information

Author Bio:
TIAN Wen(1981-), female, lecturer, PhD, tw1981@nuaa.edu.cn

摘要

摘要: 为了提高航空公司与空管方之间的协同决策程度, 降低航班延误水平, 以航路飞行的航班为研究对象, 研究了航路时空资源的多目标分配; 考虑实际运行条件下航班的唯一性约束、时间顺序约束和可行性约束的影响, 以航班在流量受限区所分配的飞行航迹和进入时隙为决策变量, 以航班总延误成本最小和航空公司延误公平损失偏差系数最小为目标函数, 构建了多目标非线性0-1整数规划模型; 基于模型特点引用了非支配排序遗传算法(NSGA-Ⅱ), 并利用排列编码法设计了一种整数基因编码方式, 以最大限度保证基因产生可行解集; 为了验证模型与算法的有效性, 基于南中国海地区航班运行实例, 对算法搜寻最优解的性能进行了研究, 并将此算法与传统按时刻表分配(RBS)方法进行了对比。研究结果表明: 改进编码方式的NSGA-Ⅱ算法使解集种群在约50代后世代距离从600收敛至30并稳定, 具有良好的收敛性; 针对实例中的多目标优化模型共生成有6组解的帕累托解集, 结果有66.7%的概率完全支配RBS方法, 且优化结果中航班平均延误成本比RBS方法降低了8.5%, 平均公平损失偏差系数降低了70.6%。可见提出的航路时空资源多目标优化方法的执行效果显著, 可在降低总延误成本的基础上兼顾各航空公司的公平性, 是解决航路飞行航班航迹与时隙资源分配问题的一种有效方法。
- 空中交通管理 /
- 航路资源分配 /
- 多目标遗传算法 /
- 协同航迹选择程序 /
- 帕累托解 /
- 基因编码
Abstract: To improve the degree of collaborative decision-making between airlines and air traffic controllers, as well as reduce the level of flight delays, air route flights were used as a research object and the multi-objective allocation of route space-time resources was studied. The effects of uniqueness, time sequence, and feasibility constraints of flights under actual operating conditions were considered and the flight trajectory and entry time slot assigned by the flight in the restricted area were viewed as decision variables. The lowest total flight delay cost and the lowest airline delay fair loss deviation coefficient were regarded as objective functions. A multi-objective nonlinear 0-1 integer programming model was constructed. Based on the characteristics of the model reference, the non-dominated sorting genetic algorithm-Ⅱ(NSGA-Ⅱ) was used and an integer gene encoding scheme was designed by the permutation encoding method. A feasible solution set was generated to maximize genes. To verify the validities of the model and algorithm, based on the South China sea area flight operation example, the performance of searching for the optimal solution was studied and the algorithm was compared with the traditional ration-by-schedule(RBS) method. Research result shows that the improved encoding style of the NSGA-Ⅱ algorithm makes the generation distance of the solution set population converge from 600 to 30 and becomes stable after approximately 50 generations, with suitable convergence. The Pareto solution set with six solutions is generated for the multi-objective optimization model, with a 66.7% probability that the RBS method is completely dominated by the results. The average flight delay cost in the optimization results is 8.5% lower than that of the RBS method, and the average fair loss deviation coefficient is 70.6% lower. The implementation effect of the multi-objective optimization method for the space-time resources of the air route is remarkable. The fairness of each airline can be considered on the basis of reducing the total delay cost, making this an effective method for solving the problem of flight trajectory and slot resource allocation.
- air traffic control /
- air route resources allocation /
- multi-objective genetic algorithm /
- collaborative trajectory options program /
- Pareto solution /
- gene encoding

HTML全文

图 1 航迹选项示例

Figure 1. Example of trajectory options

下载: 全尺寸图片幻灯片

图 2 基因编码结构

Figure 2. Gene encoding structure

下载: 全尺寸图片幻灯片

图 3 g_i取值规则流程

Figure 3. Flow of g_i value rules

下载: 全尺寸图片幻灯片

图 4 染色体G的可行解映射流程

Figure 4. Feasible solution mapping process of chromosome G

下载: 全尺寸图片幻灯片

图 5 部分匹配交叉过程示例

Figure 5. Example of partial matching cross procedure

下载: 全尺寸图片幻灯片

图 6 帕累托最优前沿

Figure 6. Pareto optimal frontiers

下载: 全尺寸图片幻灯片

图 7 世代距离

Figure 7. Generation distances

下载: 全尺寸图片幻灯片

图 8 帕累托最优解集

Figure 8. Pareto optimal solution sets

下载: 全尺寸图片幻灯片

图 9 各优化方案与RBS对比结果

Figure 9. Comparison results between each optimization scheme and RBS

下载: 全尺寸图片幻灯片

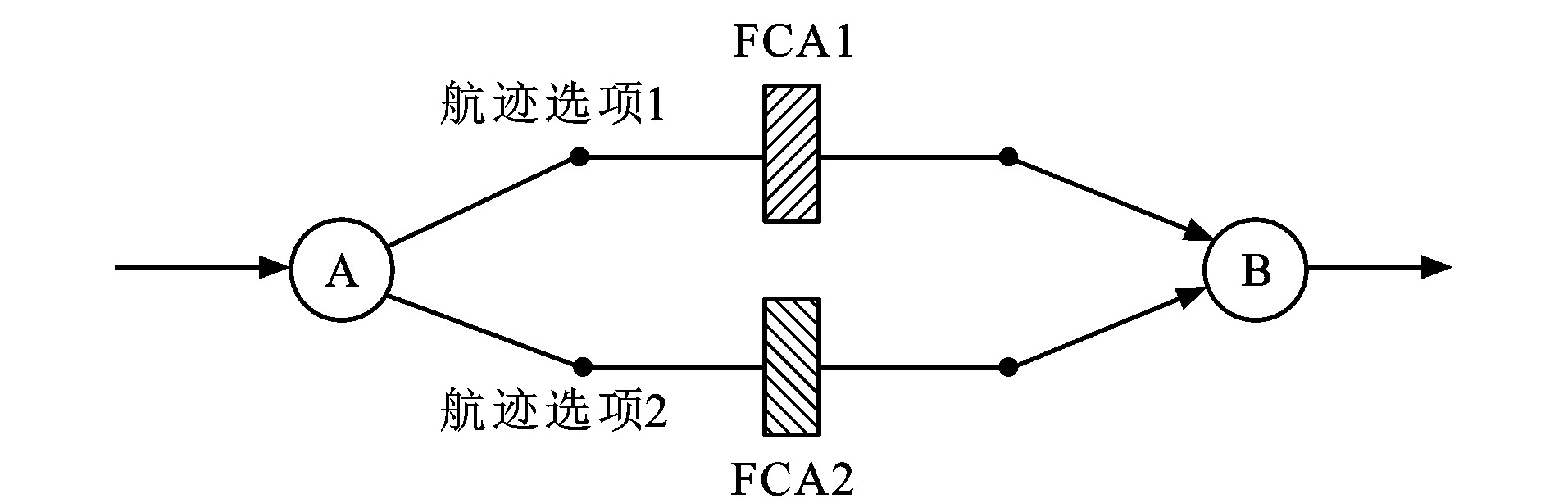
表 1 航路相关信息

Table 1. Route information

航迹	容量(个·h^-1)
FCA1	10
FCA2	12

下载: 导出CSV

表 2 可用时隙信息

Table 2. Available time slot informations

基因值	FCA1的时隙	基因值	FCA2的时隙
1	19:10:00	2	19:12:00
3	19:16:00	4	19:15:00
5	19:22:00	6	19:17:00
7	19:28:00	8	19:20:00
9	19:34:00	10	19:24:00
11	19:40:00	12	19:29:00
13	19:46:00	14	19:34:00
15	19:52:00	16	19:39:00
17	19:58:00	18	19:44:00
19	20:04:00	20	19:49:00
21	20:10:00	22	19:54:00
23	20:16:00	24	19:59:00
25	20:22:00	26	20:04:00
27	20:28:00	28	20:09:00

下载: 导出CSV

表 3 航班信息

Table 3. Flight information

航班编号	航空公司	机型	乘客数量/人次	预计进入FCA1的时间	预计进入FCA2的时间	最早进入时间
1	A	M	130	19:10:00	19:13:28	19:10:00
2	A	M	120	19:10:30	19:10:30	19:10:30
3	B	M	150	19:15:47	19:15:47	19:15:47
4	B	M	120	19:17:22	19:18:44	19:17:22
5	C	M	150	19:18:46	19:19:17	19:18:46
6	A	H	270	19:18:52	19:22:29	19:18:52
7	B	H	290	19:21:00	19:21:00	19:21:00
8	C	M	130	19:22:46	19:21:23	19:21:23
9	C	M	150	19:25:49	19:25:10	19:25:10
10	B	H	380	19:26:05	19:25:38	19:25:38
11	A	M	130	19:33:31	19:30:48	19:30:48
12	C	M	130	19:35:39	19:34:40	19:34:40
13	A	M	130	19:35:00	19:39:53	19:35:00
14	C	M	150	19:40:36	19:35:56	19:35:56
15	A	M	120	19:37:30	19:41:28	19:37:30
16	C	M	170	19:40:00	19:43:49	19:40:00
17	C	H	300	19:46:17	19:49:18	19:46:17
18	B	M	120	19:48:45	19:56:50	19:48:45
19	C	M	150	19:49:34	19:53:44	19:49:34
20	C	H	300	19:55:38	19:52:04	19:52:04
21	A	M	120	19:54:47	19:54:47	19:54:47
22	A	M	170	19:55:00	19:55:18	19:55:00
23	B	H	380	19:56:38	19:58:38	19:56:38

下载: 导出CSV

表 4 帕累托解集对应的目标值

Table 4. Target values of Pareto solution sets

航迹时隙选择方案	延误成本/min	公平损失偏差系数
1	251.55	0.076 50
2	257.18	0.012 60
3	275.48	0.011 90
4	281.33	0.011 80
5	295.55	0.005 11
6	305.06	0.001 82
平均值	277.69	0.019 96

下载: 导出CSV

参考文献(27)

[1]	徐汇晴, 田文. 基于航路资源协同分配的ATFM方法研究[J]. 航空计算技术, 2019, 49(1): 32-36, 41. doi: 10.3969/j.issn.1671-654X.2019.01.008 XU Hui-qing, TIAN Wen. Research on collaborative allocation of en-route resource for ATFM[J]. Aeronautical Computing Technique, 2019, 49(1): 32-36, 41. (in Chinese). doi: 10.3969/j.issn.1671-654X.2019.01.008
[2]	ZHU Guo-dong, WEI Peng, HOFFMAN R, et al. Centralized disaggregate stochastic allocation models for collaborative trajectory options program (CTOP)[C]∥IEEE. 37th AIAA/IEEE Digital Avionics Systems Conference (DASC). New York: IEEE, 2018: 1-10.
[3]	KAMINE S, TIEN S L, COOPER W. Analysis of AFP route-outs in preparation for CTOP post-implementation assessment[C]∥AIAA. 2013 Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2013: 1-10.
[4]	YOO H S, BRASIL C L, BUCKLEY N, et al. Impact of different trajectory option set participation levels within an air traffic management collaborative trajectory option program[C]//AIAA. 2018 Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2018: 14-25.
[5]	KIM A M. Collaborative resource allocation strategies for air traffic flow management[D]. Berkeley: University of California, Berkeley, 2011.
[6]	MURCA M C R. Collaborative air traffic flow management: incorporating airline preferences in rerouting decisions[J]. Journal of Air Transport Management, 2018, 71(1): 97-107.
[7]	YANG Shang-wen, ZHANG Jing-ting, CHEN Ping, et al. Multiobjective optimization model for collaborative en-route and slot allocation[J]. Mathematical Problems in Engineering, 2018, 1(1): 1-7.
[8]	孙晓阳, 胡明华, 张洪海. 空域和流量协同管理建模与仿真[J]. 交通运输工程学报, 2010, 10(1): 72-76. doi: 10.3969/j.issn.1671-1637.2010.01.013 SUN Xiao-yang, HU Ming-hua, ZHANG Hong-hai. Modeling and simulation of collaborative management for airspace and traffic flow[J]. Journal of Traffic and Transportation Engineering, 2010, 10(1): 72-76. (in Chinese). doi: 10.3969/j.issn.1671-1637.2010.01.013
[9]	杨赛, 胡明华, 杨尚文. 基于协同航路技术的航路资源分配方法研究[J]. 交通运输工程与信息学报, 2011, 9(4): 97-100, 118. doi: 10.3969/j.issn.1672-4747.2011.04.016 YANG Sai, HU Ming-hua, YANG Shang-wen. Research of route allocation methods based on collaborative routing technology[J]. Journal of Transportation Engineering and Information, 2011, 9(4): 97-100, 118. (in Chinese). doi: 10.3969/j.issn.1672-4747.2011.04.016
[10]	HO-HUU V, HARTIES S, VISSER H G, et al. An optimization framework for route design and allocation of aircraft to multiple departure routes[J]. Transportation Research Part D: Transport and Environment, 2019, 76(1): 273-288.
[11]	刘方勤, 胡明华, 张颖. 基于航路耦合容量的协同多航路资源分配[J]. 航空学报, 2011, 32(4): 672-684. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201104012.htm LIU Fang-qin, HU Ming-hua, ZHANG Yin. Collaborative multiple en-route airspace resource rationing based on en-route capacity under coupling constraints[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(4): 672-684. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201104012.htm
[12]	CHURCHILL A M, LOVELL D J. Coordinated aviation network resource allocation under uncertainty[J]. Transportation Research Part E: Logistics and Transportation Review, 2012, 48(1): 19-33. doi: 10.1016/j.tre.2011.05.006
[13]	RODIONOVA O, ARENSON H, SRIDHAR B, et al. Efficient trajectory options allocation for the collaborative trajectory options program[C]//IEEE. 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC). New York: IEEE, 2018: 1-10.
[14]	CASTELLI L, PESENTI R, RANIERI A. The design of a market mechanism to allocate air traffic flow management slots[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(5): 931-943. doi: 10.1016/j.trc.2010.06.003
[15]	KIM A, HANSEN M. A framework for the assessment of collaborative en route resource allocation strategies[J]. Transportation Research Part C: Emerging Technologies, 2013, 33(8): 324-339.
[16]	KIM A, HANSEN M. Some insights into a sequential resource allocation mechanism for en route air traffic management[J]. Transportation Research Part B: Methodological, 2015, 79(9): 1-15.
[17]	KIM B. Two-stage combinatorial optimization framework for air traffic flow management under constrained capacity[D]. Atlanta: Georgia Institute of Technology, 2015.
[18]	杨尚文, 陈平, 童明. 基于航班时刻不确定性的航路时隙分配模型[J]. 交通信息与安全, 2019, 37(6): 156-162. https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201906020.htm YANG Shang-wen, CHEN Ping, TONG Ming. A model of en-route and slot allocation based on uncertainty of flight time[J]. Journal of Transportation Information and Safety, 2019, 37(6): 156-162. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JTJS201906020.htm
[19]	张洪海, 胡明华. 多跑道降落飞机协同调度优化[J]. 交通运输工程学报, 2009, 9(3): 86-91. doi: 10.3321/j.issn:1671-1637.2009.03.017 ZHANG Hong-hai, HU Ming-hua. Multi-runway collaborative scheduling optimization of aircraft landing[J]. Journal of Traffic and Transportation Engineering, 2009, 9(3): 86-91. (in Chinese). doi: 10.3321/j.issn:1671-1637.2009.03.017
[20]	徐兆龙, 姜雨, 罗宇骁, 等. 基于蚁群算法的多跑道航班协同调度建模[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38(6): 1362-1366, 1371. doi: 10.3963/j.issn.2095-3844.2014.06.041 XU Zhao-long, JIANG Yu, LUO Yu-xiao, et al. Modeling of collaborative scheduling of flights on multi-runways based on ant colony algorithm[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2014, 38(6): 1362-1366, 1371. (in Chinese). doi: 10.3963/j.issn.2095-3844.2014.06.041
[21]	王璐, 张小宁, 孙智慧, 等. 效益和公平性的多跑道航班调度精确算法研究[J]. 航空计算技术, 2017, 47(2): 25-28. doi: 10.3969/j.issn.1671-654X.2017.02.007 WANG Lu, ZHANG Xiao-ning, SUN Zhi-hui, et al. Exact algorithm for multi-runway scheduling of flights at airports considering airline company profits and fairness[J]. Aeronautical Computing Technique, 2017, 47(2): 25-28. (in Chinese). doi: 10.3969/j.issn.1671-654X.2017.02.007
[22]	GANJI M, LOVELL D J, BALL M O, et al. Resource allocation in flow-constrained areas with stochastic termination times[J]. Transportation Research Record, 2009(2106): 90-99.
[23]	张洪海, 胡明华. 多跑道着陆飞机协同调度多目标优化[J]. 西南交通大学学报, 2009, 44(3): 402-409. doi: 10.3969/j.issn.0258-2724.2009.03.017 ZHANG Hong-hai, HU Ming-hua. Multi-objective optimization for collaborative scheduling aircraft landing on multi-runways[J]. Journal of Southwest Jiaotong University, 2009, 44(3): 402-409. (in Chinese). doi: 10.3969/j.issn.0258-2724.2009.03.017
[24]	余朝军, 江驹, 徐海燕, 等. 基于改进遗传算法的航班-登机口分配多目标优化[J]. 交通运输工程学报, 2020, 20(2): 121-130. doi: 10.19818/j.cnki.1671-1637.2020.02.010 YU Chao-jun, JIANG Ju, XU Hai-yan, et al. Multi-objective optimization of flight-gate assignment based on improved genetic algorithm[J]. Journal of Traffic and Transportation Engineering, 2020, 20(2): 121-130. (in Chinese). doi: 10.19818/j.cnki.1671-1637.2020.02.010
[25]	万莉莉, 胡明华, 田勇, 等. 终端区进离场资源分配优化模型[J]. 交通运输工程学报, 2016, 16(2): 109-117. http://transport.chd.edu.cn/article/id/201602013 WAN Li-li, HU Ming-hua, TIAN Yong, et al. Optimization model of arrival and departure resource allocation in terminal area[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 109-117. (in Chinese). http://transport.chd.edu.cn/article/id/201602013
[26]	WANG Yong, ASSOGBA K, LIU Yong, et al. Two-echelon location-routing optimization with time windows based on customer clustering[J]. Expert Systems with Applications, 2018, 104(8): 244-260.
[27]	VELDHUIZEN D A, LAMONT G B. Evolutionary computation and convergence to a pareto front[C]//Stanford University. Proceedings of the 1998 Genetic Programming Conference. Stanford: Stanford University, 1998: 221-228.