Train passing analysis on large-span railway suspension bridge based on ANSYS-MATLAB co-simulation
-
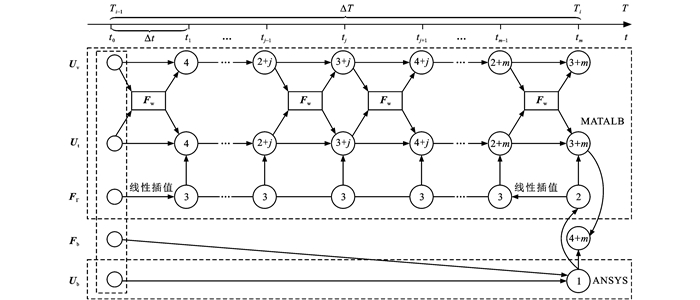
摘要: 针对大跨铁路悬索桥结构复杂、几何非线性显著的特点开展行车动力分析，提出了一种ANSYS与MATLAB实时交互、联合仿真的列车-轨道-桥梁耦合振动分析方法; 在ANSYS内建立悬索桥和轨道结构精细有限元模型，在MATLAB内基于多刚体动力学理论组装车辆质量、阻尼和刚度矩阵，并将轨道结构动力微分方程系数矩阵导至MATLAB中; 分别建立悬索桥子系统、轨道-车辆子系统的动力微分方程，然后基于异步长策略，以大时间步长在ANSYS内考虑主缆几何刚度，并通过更新结构刚度矩阵来求解悬索桥子系统振动响应，以小时间步长在MATLAB内考虑轮轨空间接触关系，并通过施加轨道不平顺来求解轨道-车辆子系统动力响应，2种计算软件通过实时交换数据实现子系统之间的耦合求解; 通过分析某单跨铁路简支梁桥的实测数据验证了该方法的正确性，并利用该联合仿真方法对主跨为660 m的某铁路悬索桥进行了行车动力计算。分析结果表明：随着车速的提高，桥梁动力响应增大，行车安全性与平稳性趋于恶化; 在车速不大于180 km·h-1的工况下，该悬索桥能够满足行车安全性要求; 在列车动力荷载作用下，不考虑悬索桥几何刚度会导致跨中竖向位移产生7.4%的计算误差; 考虑几何刚度、不更新桥梁刚度矩阵导致的桥梁与列车响应计算误差均不超过1%，能够满足工程计算精度需求。可见，提出的联合仿真方法可用于大跨柔性铁路桥梁的行车动力分析。
-
关键词:
- 桥梁工程 /
- 大跨铁路悬索桥 /
- ANSYS-MATLAB联合仿真 /
- 列车-轨道-桥梁耦合振动 /
- 几何非线性 /
- 异步长
Abstract: To study the driving dynamics of large-span railway suspension bridges with complex structures and significant geometric nonlinearity, a train-track-bridge coupled vibration analysis method was introduced based on the real-time interacting ANSYS-MATLAB co-simulation. The refined finite element models of suspension bridge and track structure were established in ANSYS. The mass, damping, and stiffness matrices of train were assembled in MATLAB according to the multi-rigid-body dynamics theory, and the dynamic differential equation coefficient matrices of track structure were exported to MATLAB. The dynamic differential equations of suspension bridge subsystem and track-train subsystem were established separately. Then, based on the multi-time-step strategy, the vibration responses of suspension bridge subsystem were calculated by considering the geometric stiffness of main cables and updating the stiffness matrices of structure in ANSYS with coarse time steps. The dynamic responses of track-train subsystem were calculated by considering the wheel-rail spatial contact relationship and applying track irregularities in MATLAB with fine time steps. The coupling solution between subsystems was realized via the real-time data exchange between ANSYS and MATLAB. The method was verified by analyzing the test data of a railway simply supported beam bridge with single span. The co-simulation method was applied to a 660 m-long railway suspension bridge to analyze the driving dynamics. Analysis result shows that the dynamic responses of bridge tend to increase and the driving safety and stability tend to deteriorate as the speed of train increases. The suspension bridge design can fulfil the safety requirements when the train speed does not exceed 180 km·h-1. Under the train dynamic loads, neglecting the geometric stiffness of suspension bridge results in an calculation error of 7.4% in the midspan vertical displacement. Considering the geometric stiffness without updating the bridge stiffness matrix leads to a calculation error less than 1% for the bridge and train responses. The results satisfy the required calculation accuracy. Therefore, the proposed co-simulation method can be used to analyze the driving dynamics of large-span flexible railway bridges. 4 tabs, 14 figs, 31 refs. -
图 7 简支梁桥跨中竖向位移
Figure 7. Midspan vertical displacement of simply supported beam bridge
图 10 典型工况中主梁跨中轨下桥面板动力响应时程
Figure 10. Dynamic responses time histories of bridge deck of midspan section below track under typical working conditions
图 11 工况3中跨主缆应力时程
Figure 11. Stress time history of midspan main cable in working condition 3
图 14 首节车第1轮对左侧轮轨力
Figure 14. Left wheel-rail forces of first wheel-set of first vehicle
表 1 悬索桥模态分析结果
Table 1. Modal analysis result of suspension bridge
表 2 工况设置
Table 2. Working condition setting
工况 车速/(km·h-1) 单/双线 是否考虑几何刚度 是否更新刚度矩阵 1 80 单 是 是 2 100 单 是 是 3 120 单 是 是 4 140 单 是 是 5 160 单 是 是 6 180 单 是 是 7 120 双 是 是 8 120 单 否 否 9 120 单 是 否 
下载: 导出CSV
表 3 桥梁最大动力响应
Table 3. Maximum dynamic responses of bridge
工况 位移/mm 加速度/(m·s-2) 左跨1/2截面轨下桥面板 中跨1/4截面轨下桥面板 中跨1/2截面轨下桥面板 左跨1/2截面轨下桥面板 中跨1/4截面轨下桥面板 中跨1/2截面轨下桥面板 横向 竖向 横向 竖向 横向 竖向 横向 竖向 横向 竖向 横向 竖向 1 0.2 -4.2 0.4 86.7 0.5 121.2 0.021 2 0.285 4 0.013 2 0.311 7 0.013 2 0.378 0 2 0.2 -4.2 0.3 86.9 0.4 121.6 0.021 0 0.380 9 0.015 8 0.405 7 0.013 8 0.531 4 3 0.2 -4.2 0.3 87.1 0.4 121.8 0.026 7 0.509 0 0.019 2 0.636 0 0.019 1 0.704 0 4 0.2 -4.2 0.3 87.4 0.4 122.3 0.030 9 0.666 8 0.027 4 0.739 5 0.025 0 0.863 6 5 0.2 -4.2 0.3 87.9 0.3 122.5 0.035 9 0.845 0 0.030 9 0.931 0 0.030 2 1.087 1 6 0.2 -4.2 0.3 88.1 0.3 123.6 0.036 8 0.966 1 0.032 7 1.133 6 0.036 9 1.358 7 7 0.2 -4.8 0.2 138.2 0.1 239.4 0.028 7 0.508 7 0.044 4 1.074 1 0.031 0 0.514 9 8 0.2 -4.4 0.2 93.7 0.2 130.7 0.026 4 0.619 8 0.024 9 0.670 2 0.024 0 0.806 8 9 0.2 -4.2 0.2 86.6 0.3 121.0 0.025 6 0.618 2 0.024 6 0.651 0 0.023 2 0.760 7
下载: 导出CSV
表 4 最大车辆动力响应
Table 4. Maximum dynamic responses of vehicles
工况 动车 拖车 加速度/(m·s-2) 脱轨系数 轮轴横向力/kN 轮重减载率 加速度/(m·s-2) 脱轨系数 轮轴横向力/kN 轮重减载率 横向 竖向 横向 竖向 1 0.180 1 0.161 0 0.104 0 11.148 0.199 8 0.199 4 0.180 8 0.110 4 10.809 0.221 3 2 0.207 3 0.194 6 0.114 0 13.644 0.128 5 0.233 6 0.221 8 0.120 7 12.869 0.133 1 3 0.236 0 0.227 8 0.130 1 14.980 0.165 6 0.260 5 0.257 1 0.134 2 14.390 0.163 6 4 0.258 1 0.259 7 0.138 1 14.850 0.206 9 0.288 5 0.293 4 0.145 8 14.919 0.199 5 5 0.272 8 0.288 1 0.136 2 15.481 0.273 6 0.312 8 0.328 2 0.148 3 15.264 0.246 8 6 0.282 6 0.314 2 0.161 5 16.851 0.307 4 0.327 4 0.361 3 0.178 8 16.934 0.268 0 7 0.235 9 0.252 4 0.131 2 15.130 0.165 8 0.260 6 0.280 5 0.134 9 14.513 0.159 8 8 0.236 0 0.229 3 0.130 2 14.448 0.165 8 0.260 6 0.259 8 0.134 2 14.772 0.163 9 9 0.235 9 0.227 6 0.129 9 14.980 0.166 4 0.260 5 0.257 0 0.134 0 14.388 0.164 6
下载: 导出CSV
-
[1] 陈良江, 周勇政. 我国高速铁路桥梁技术的发展与实践[J]. 高速铁路技术, 2020, 11(2): 27-32. https://www.cnki.com.cn/Article/CJFDTOTAL-GSTL202002006.htmCHEN Liang-jiang, ZHOU Yong-zheng. Development and practice of high-speed railway bridge technology in China[J]. High Speed Railway Technology, 2020, 11(2): 27-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GSTL202002006.htm [2] 李迎九. 千米跨度高速铁路悬索桥建造技术现状与展望[J]. 中国铁路, 2019(9): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-TLZG201909001.htmLI Ying-jiu. Current situation and expectation of construction technology for HSR suspension bridge with kilometers span[J]. China Railway, 2019(9): 1-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TLZG201909001.htm [3] 李永乐, 蔡宪棠, 安伟胜, 等. 大跨度铁路悬索桥结构刚度敏感性研究[J]. 中国铁道科学, 2011, 32(4): 24-30. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201104007.htmLI Yong-le, CAI Xian-tang, AN Wei-sheng, et al. Study on the sensitivity of the structural stiffness of long-span railway suspension bridge[J]. China Railway Science, 2011, 32(4): 24-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201104007.htm [4] 沈锐利, 张东, 唐茂林. 大跨度铁路悬索桥合理刚度指标值的探讨[C]//中国土木工程学会. 2012年全国桥梁学术大会论文集. 北京: 人民交通出版社, 2012: 223-239.SHEN Rui-li, ZHANG Dong, TANG Mao-lin. Discussion on rational stiffness index of long-span railway suspension bridge[C]//Chinese Society of Civil Engineering. Proceedings of 2012 National Bridge and Structure Academic Conference. Beijing: China Communications Press, 2012: 233-239. (in Chinese) [5] 唐贺强, 徐恭义, 刘汉顺. 悬索桥用于铁路桥梁的可行性分析[J]. 桥梁建设, 2017, 47(2): 13-18. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201702003.htmTANG He-qiang, XU Gong-yi, LIU Han-shun. Feasibility analysis of applying of suspension bridge type to railway bridges[J]. Bridge Construction, 2017, 47(2): 13-18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201702003.htm [6] ZHAI Wan-ming, HAN Zhao-ling, CHEN Zhao-wei, et al. Train-track-bridge dynamic interaction: a state-of-the-art review[J]. Vehicle System Dynamics, 2019, 57(7): 984-1027. doi: 10.1080/00423114.2019.1605085 [7] 周智辉, 曾庆元. 桥上列车脱轨计算分析[J]. 中国铁道科学, 2004, 25(4): 47-50. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200404008.htmZHOU Zhi-hui, ZENG Qing-yuan. Computation and analysis of train derailment on bridge[J]. China Railway Science, 2004, 25(4): 47-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200404008.htm [8] DINH V N, KIM K D, WARNITCHAI P. Dynamic analysis of three-dimensional bridge-high-speed train interactions using a wheel-rail contact model[J]. Engineering Structures, 2009, 31(12): 3090-3106. doi: 10.1016/j.engstruct.2009.08.015 [9] ANTOLÍN P, ZHANG Nan, GOICOLEA J M, et al. Consideration of nonlinear wheel-rail contact forces for dynamic vehicle-bridge interaction in high-speed railways[J]. Journal of Sound and Vibration, 2013, 332(5): 1231-1251. doi: 10.1016/j.jsv.2012.10.022 [10] LI Q, XU Y L, WU D J, et al. Computer-aided nonlinear vehicle-bridge interaction analysis[J]. Journal of Vibration and Control, 2010, 16(12): 1791-1816. doi: 10.1177/1077546309341603 [11] ZHAI Wan-ming. Two simple fast integration methods for large-scale dynamic problems in engineering[J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 4199-4214. doi: 10.1002/(SICI)1097-0207(19961230)39:24<4199::AID-NME39>3.0.CO;2-Y [12] ZHAI Wan-ming, XIA He, CAI Cheng-biao, et al. High-speed train-track-bridge dynamic interactions—Part Ⅰ: theoretical model and numerical simulation[J]. International Journal of Rail Transportation, 2013, 1(1/2): 3-24. [13] 吴定俊, 李奇, 陈艾荣. 车桥耦合振动迭代求解数值稳定性问题[J]. 力学季刊, 2007, 28(3): 405-411. doi: 10.3969/j.issn.0254-0053.2007.03.009WU Ding-jun, LI Qi, CHEN Ai-rong. Numerical stability of iteration scheme for solution vehicle-bridge coupling vibration[J]. Chinese Quarterly of Mechanics, 2007, 28(3): 405-411. (in Chinese) doi: 10.3969/j.issn.0254-0053.2007.03.009 [14] ZHU Zhi-hui, GONG Wei, WANG Li-dong, et al. An efficient multi-time-step method for train-track-bridge interaction[J]. Computers and Structures, 2018, 196: 36-48. doi: 10.1016/j.compstruc.2017.11.004 [15] 张楠, 夏禾. 基于全过程迭代的车桥耦合动力系统分析方法[J]. 中国铁道科学, 2013, 34(5): 32-38. doi: 10.3969/j.issn.1001-4632.2013.05.06ZHANG Nan, XIA He. A vehicle-bridge interaction dynamic system analysis method based on inter-system iteration[J]. China Railway Science, 2013, 34(5): 32-38. (in Chinese) doi: 10.3969/j.issn.1001-4632.2013.05.06 [16] YU Zhi-wu, MAO Jian-feng. Probability analysis of train-track-bridge interactions using a random wheel/rail contact model[J]. Engineering Structures, 2017, 144: 120-138. doi: 10.1016/j.engstruct.2017.04.038 [17] XIA H, XU Y L, CHAN T H T. Dynamic interaction of long suspension bridges with running trains[J]. Journal of Sound and Vibration, 2000, 237(2): 263-280. doi: 10.1006/jsvi.2000.3027 [18] 郭向荣, 何玮, 朱志辉, 等. 横风作用下货物列车通过大跨度铁路斜拉桥的走行安全性研究[J]. 中国铁道科学, 2016, 37(2): 41-47. doi: 10.3969/j.issn.1001-4632.2016.02.06GUO Xiang-rong, HE Wei, ZHU Zhi-hui, et al. Running safety of freight train passing long-span cable-stayed railway bridge under cross wind[J]. China Railway Science, 2016, 37(2): 41-47. (in Chinese) doi: 10.3969/j.issn.1001-4632.2016.02.06 [19] 韩艳, 夏禾, 郭薇薇. 斜拉桥在地震与列车荷载同时作用下的动力响应分析[J]. 工程力学, 2006, 23(1): 93-98. doi: 10.3969/j.issn.1000-4750.2006.01.018HAN Yan, XIA He, GUO Wei-wei. Dynamic response of cable-stayed bridge to running trains and earthquakes[J]. Engineering Mechanics, 2006, 23(1): 93-98. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.01.018 [20] GONG Wei, ZHU Zhi-hui, LIU Yu, et al. Running safety assessment of a train traversing a three-tower cable-stayed bridge under spatially varying ground motion[J]. Railway Engineering Science, 2020, 28(2): 184-198. doi: 10.1007/s40534-020-00209-8 [21] ZHU Zhi-hui, GONG Wei, WANG Kun, et al. Dynamic effect of heavy-haul train on seismic response of railway cable-stayed bridge[J]. Journal of Central South University, 2020, 27(7): 1939-1955. doi: 10.1007/s11771-020-4421-z [22] 李小珍, 秦羽, 刘德军, 等. 侧风作用下五峰山长江大桥列车行车安全控制[J]. 铁道工程学报, 2018(7): 58-64. doi: 10.3969/j.issn.1006-2106.2018.07.011LI Xiao-zhen, QIN Yu, LIU De-jun, et al. The safety control of train running on the Wufeng Mountain Yangtze River Bridge under crosswind[J]. Journal of Railway Engineering Society, 2018(7): 58-64. (in Chinese) doi: 10.3969/j.issn.1006-2106.2018.07.011 [23] 雷虎军, 刘伟, 黄炳坤. 地震作用下千米级高速铁路悬索桥行车安全性研究[J]. 振动与冲击, 2020, 39(10): 249-255. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010035.htmLEI Hu-jun, LIU Wei, HUANG Bing-kun. Running safety of high-speed railway kilometre-level suspension bridge under earthquake[J]. Journal of Vibration and Shock, 2020, 39(10): 249-255. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010035.htm [24] YAU J D. Dynamic response analysis of suspended beams subjected to moving vehicles and multiple support excitations[J]. Journal of Sound and Vibration, 2009, 325(4/5): 907-922. http://www.sciencedirect.com/science/article/pii/S0022460X09003216 [25] 谢铠泽, 赵维刚, 蔡小培, 等. 悬索桥初始内力与几何非线性对梁轨相互作用的影响[J]. 交通运输工程学报, 2020, 20(1): 82-91. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202001009.htmXIE Kai-ze, ZHAO Wei-gang, CAI Xiao-pei, et al. Impacts of initial internal force and geometric nonlinearity of suspension bridge on bridge-rail interaction[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 82-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202001009.htm [26] 翟婉明, 蔡成标, 王开云. 高速列车-轨道-桥梁动态相互作用原理及模型[J]. 土木工程学报, 2005, 38(11): 132-137. doi: 10.3321/j.issn:1000-131X.2005.11.024ZHAI Wan-ming, CAI Cheng-biao, WANG Kai-yun. Mechanism and model of high-speed train-track-bridge dynamic interaction[J]. China Civil Engineering Journal, 2005, 38(11): 132-137. (in Chinese) doi: 10.3321/j.issn:1000-131X.2005.11.024 [27] KALKER J J. On the rolling contact of two elastic bodies in the presence of dry friction[D]. Delt: Delt University of Technology, 1967. [28] VERMEULEN P J, JOHNSON K L. Contact of nonspherical elastic bodies transmitting tangential forces[J]. Journal of Applied Mechanics, 1964, 31(2): 338-340. doi: 10.1115/1.3629610 [29] NOUR-OMID B, RANKIN C C. Finite rotation analysis and consistent linearization using projectors[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93(3): 353-384. doi: 10.1016/0045-7825(91)90248-5 [30] ZHU Zhi-hui, GONG Wei, WANG Li-dong, et al. Efficient assessment of 3D train-track-bridge interaction combining multi-time-step method and moving track technique[J]. Engineering Structures, 2019, 183: 290-302. doi: 10.1016/j.engstruct.2019.01.036 [31] 杨海洋, 钟铁毅, 夏禾. 铁路悬索桥纵向非一致激励地震响应分析[J]. 振动与冲击, 2014, 33(22): 157-163. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201422028.htmYANG Hai-yang, ZHONG Tie-yi, XIA He. Seismic responses analysis of a railway suspension bridge under longitudinal non-uniform excitations[J]. Journal of Vibration and Shock, 2014, 33(22): 157-163. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201422028.htm -
点击查看大图
图(14) / 表(4)
计量
- 文章访问数: 762
- HTML全文浏览量: 466
- PDF下载量: 198
- 被引次数: 0
