Design method for asymmetric grinding profile of rails in sharp curves
-
摘要: 为设计可提升列车小半径曲线通过性能的钢轨非对称打磨目标廓形,对中国现有CN60钢轨廓形进行了几何推导;以钢轨廓形几何参数作为设计变量,以车辆系统多体动力学指标作为综合目标函数,考虑钢轨打磨约束条件,提出了一种针对小半径曲线钢轨非对称打磨廓形的多目标数值优化模型;基于差分进化算法编写了相应的数值计算程序,并选择合理的计算参数求解了优化模型;根据实际线路参数分析了优化后钢轨打磨廓形的轮轨接触几何特性,并验证了列车的小半径曲线动力学性能。研究结果表明:提出的优化方法具有较快的计算速度,优化模型仅迭代了97次即可获得理想的钢轨打磨廓形;非对称打磨使内外钢轨具有差异性的打磨位置与打磨深度,将轮轨对中位置向轨道内侧移动了约10 mm,且不会改变轮缘处的轮轨匹配特性,有效增大了轮对横移10 mm范围内的轮对滚动圆半径差与轮轨接触角差,降低了列车在通过小半径曲线时的轮对横移、轮轨横向力、脱轨系数和轮重减载率,提高了转向架的横向稳定性和轮轨磨耗性能;虽然该打磨方式获得的钢轨廓形增大了轮轨接触应力,但并不会引起轮轨塑性变形。由此可见,该设计方法为提高列车的中小半径曲线通过能力提供了一种可行途径。Abstract: For improving the performance of trains passing through sharp curves, the geometric derivation was performed on the profile of existing CN60 rails in China to design the target rail profile by asymmetric grinding. Taking the geometric parameters of the rail profile as design variables and the multi-body dynamics index of vehicle system as the comprehensive objective function, a multi-objective numerical optimization model for the asymmetric grinding profile of rails in sharp curves was proposed considering the rail grinding constraints. On the basis of the differential evolution algorithm, the corresponding numerical calculation program was written, and reasonable calculation parameters were selected to solve the optimization model. According to the actual line parameters, the wheel-rail contact geometric characteristics of the optimized grinding profile of rails were analyzed, and the dynamics performance of trains passing through sharp curves was verified. Research results reveal that the proposed optimization method is fast in calculations, and the ideal grinding profile of rails can be obtained after only 97 iterations of the optimization model. Due to the asymmetric grinding, the inner and outer rails have different grinding positions and grinding depths, and the centering positions of wheels and rails move to the inner side of rails by about 10 mm, without any change in the wheel-rail matching characteristics at the flange. This effectively increases the wheelset rolling radius difference and the difference in wheel-rail contact angles in the wheelset lateral displacement range of 10 mm, reduces the lateral displacement of wheelset, lateral wheel-rail force, derailment coefficient, and rate of wheel load reduction when trains pass through sharp curves, and improves the lateral stability of the bogie and the wheel-rail wear performance. Although the rail profile obtained by this grinding method increases the wheel-rail contact stress, it does not cause the plastic wheel-rail deformation. Therefore, this design method is feasible to improve the capability of trains passing through small- and medium-radius curves. 3 tabs, 16 figs, 31 refs.
-
0. 引言
随着社会经济发展,铁路列车急需提高运输效率,以满足人民日益增长的运输需求,但提升运输效率的前提是保证列车安全、稳定的运行[1-4]。曲线通过性能一直以来都是影响列车运行的关键问题[5],当列车全速通过曲线时,将造成较大的轮轨作用力,从而降低了列车的动力学性能,甚至威胁行车安全[6-7],这也是小半径曲线线路对列车进行限速的主要原因之一,因此,提升列车的小半径曲线通过性能对提高列车运输效率具有重要意义。在既有线路养护工作中,工务部门常采用钢轨打磨技术[8-10]对钢轨进行维护,以提升列车的曲线通过性能。钢轨打磨是通过打磨机械或打磨车上的砂轮清除钢轨表面损伤,降低因钢轨磨耗损伤引起的轮轨间作用力,获得与车轮踏面匹配良好的钢轨廓形,使轮轨具有较好的接触特性,并改善列车的动力学性能。当列车以较高速度通过小半径曲线时,为获得列车所需的转向力矩,轮对将向外轨偏移以获得更大的轮径差,因此,对小半径曲线线路钢轨采用非对称打磨[11-13]形式将更有利于提高列车的曲线通过性能。
就钢轨打磨技术而言,钢轨打磨目标廓形是整个打磨的关键所在,它指导着钢轨打磨工作的进行,直接决定了最终的打磨效果。目前对钢轨打磨廓形的研究中:Smallwood等[14]针对轮轨最大接触压力和曲线轮轨接触特性,对曲线钢轨廓形进行了优化设计,最终使轮轨接触特性得到提升;Magel等[15-16]面向轮轨磨耗、轮轨疲劳和钢轨波磨问题,基于轮轨接触关系对钢轨打磨廓形进行了优化,证明合理的钢轨廓形可以有效降低轮轨磨耗;崔大宾等[17-19]以降低轮轨接触应力为目标,采用序列二次规划法设计了一种钢轨打磨廓形,保证了左右轮轨磨耗程度相对均匀,且不会影响车辆动力学性能;Zhai等[20]基于轮轨动态作用力提出了一种解决重载铁路曲线侧磨的非对称钢轨廓形设计方法,要求曲线钢轨非对称打磨应满足减小轮轨接触应力和增大轮对滚动圆半径差这2个必要原则;毛鑫等[21]以轮对滚动圆半径差为优化目标,反求设计出一种钢轨打磨廓形,提高了轮轨接触性能;陈步琛等[22]以轮径差函数为核心目标,以预期轮轨接触分布为边界,提出了一种逆向反推设计钢轨打磨目标廓形的算法,提升了轮轨匹配特性;林凤涛等[23-25]以减少打磨量和脱轨系数为目的设计了一种钢轨打磨廓形,使优化后的钢轨廓形具有较好的经济性,同时采用双打磨策略延长了曲线区段钢轨的使用寿命。
从上述研究中不难发现,小半径曲线钢轨打磨廓形设计的目的是增大轮对滚动圆半径差和减小轮轨磨耗,最终提升列车的曲线通过性能。鉴于此,本文以提速货运线路为研究对象,推导了钢轨廓形曲线的几何关系,以圆弧半径和切点坐标作为优化变量,以列车通过曲线时的动力学性能指标作为优化目标,提出了一种曲线钢轨非对称打磨廓形的数值优化模型,并采用差分进化(Differential Evolution, DE)算法进行求解,设计出小半径曲线钢轨非对称打磨廓形,并获得了理论验证。
1. 数学模型
1.1 设计变量
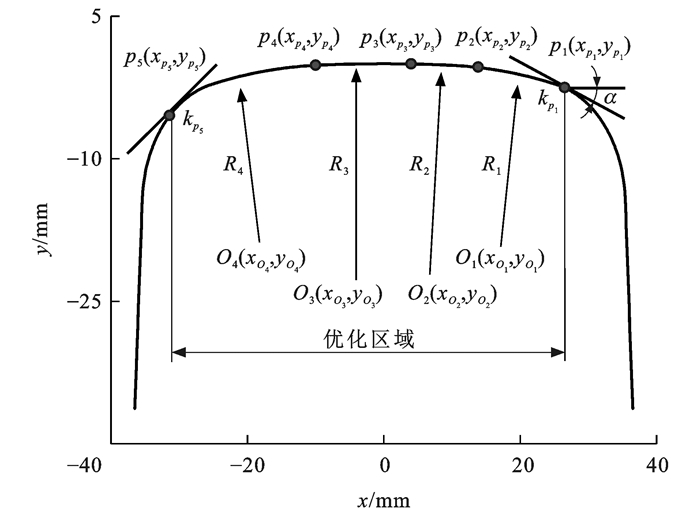
为建立数值优化模型,对提速货运线路所采用的CN60钢轨廓形进行几何推导,图 1为CN60钢轨截面在平面直角坐标系下的几何表达,其中x和y分别为钢轨横、垂向坐标。
首先根据轮轨接触区域确定钢轨的优化区域,优化区域的边界点p1(xp1, yp1)和p5(xp5, yp5)为固定点,其切线斜率分别为kp1和kp5。优化区域内的廓形曲线表示为4段连续相切的圆弧1~4。O1(xO1, yO1)~O4(xO4, yO4)分别为各圆弧的圆心坐标;R1~R4分别为各圆弧的半径;p2(xp2, yp2)~ p4(xp4, yp4)分别为4段圆弧的相切点。利用解析几何公式可推导出廓形中各参数的几何关系。
α为p1处切线与水平线的夹角,则其可由kp1计算得
α=arctan(|kp1|) (1) 由于圆弧1与固定点p1相切,则圆心O1的坐标为
{xO1=xp1−R1sin(α)yO1=yp1−R1cos(α) (2) p2是圆弧1与圆弧2的切点,因此,yp2满足
yp2=yO1+√R21−(xp2−xO1)2 (3) 由于圆弧1与圆弧2相切,此时圆心O1、O2与切点p2共线,设该线为l12,则此时圆心O2坐标满足
{k12=(yp2−yO1)/(xp2−xO1)b12=−k12xO1+yO1yp2=yO2+√R22−(xp2−xO2)2yO2=k12xO2+b12 (4) 式中:k12与b12分别为直线l12的斜率和截距。
需要注意的是,式(4)本质上是利用过已知点的两圆弧相切性质对圆心进行求解,所解出的圆心存在2个解,但由钢轨廓形几何曲线的强凸性,圆心应取两圆弧内切解。
同理,圆弧2、3的切点p3与圆心O3的坐标满足
{yp3=yO2+√R22−(xp3−xO2)2yp3=yO3+√R23−(xp3−xO3)2k23=(yp3−yO2)/(xp3−xO2)b23=−k23xO2+yO2yO3=k23xO3+b23 (5) 式中:k23和b23分别为圆心O2、O3与切点p3连线l23的斜率和截距。
p4为圆弧3与圆弧4的切点,yp4可由圆弧3计算为
yp4=yO3+√R23−(xp4−xO3)2 (6) 由于p5是固定点,且p4和p5都在圆弧4上,因此,圆弧4的圆心O4及其半径R4满足
{k34=(yp4−yO3)/(xp4−xO3)b34=−k34xO3+yO3yO4=k34xO4+b34R4=√(xp5−xO4)2+(yp5−yO4)2R4=√(xp4−xO4)2+(yp4−yO4)2 (7) 式中:k34和b34分别为圆心O3、O4与切点p4连线l34的斜率和截距。
至此,钢轨优化区域内各廓形参数都可由圆弧半径R1、R2、R3和圆弧切点横坐标xp2、xp3、xp4表达,将这6个未知量作为模型的优化变量vs,即
vs=(R1,R2,R3,xp2,xp3,xp4) (8) 4段相切圆弧Ci可表示为
Ci=fi(vs) (9) 式中:fi(vs)(i=1, 2, 3, 4)为圆弧段i的解析方程。
优化区域内的钢轨廓形曲线Cr可表示为
Cr=fr(vs) (10) 式中:fr(vs)为优化区域圆弧的解析方程。
由于小半径曲线钢轨采用非对称打磨,左右钢轨的打磨参数并不相同,需单独优化左右钢轨设计变量,则模型变量可表示为
v=(vs1,vsr) (11) 式中:vsl和vsr分别为左右侧钢轨变量。
1.2 目标函数
本文以列车通过小半径曲线时的综合动力学性能指标作为钢轨廓形设计目标。目前只设计线路上的圆曲线廓形,直线钢轨保持原有的标准廓形,在缓和曲线段设置渐变截面钢轨以最大程度逼近实际线路,曲线线路参数设置如表 1所示。
表 1 小半径曲线仿真参数Table 1. Simulation parameters of sharp curve参数 数值 两端直线长度/m 100 两端缓和曲线长度/m 100 曲线半径/m 800 曲线长度/m 300 线路超高/mm 100 采样频率/Hz 200 运行速度/(km·h-1) 90 根据提速货物列车性能要求,选择列车通过小半径曲线时的脱轨系数、轮重减载率和轮轴横向力作为目标函数,则目标函数可确定为
min (12) 式中:Ql和Qr分别为左右侧轮轨横向力;Pl和Pr分别为左右侧轮轨垂向力;ΔP为左右侧轮轨垂向力之差;P为左右侧轮轨平均垂向力;f1(v)为左右车轮的最大脱轨系数;f2(v)为最大轮重减载率;f3(v)为最大轮轴横向力。
式(12)为多目标函数,为便于计算,将多目标函数设计为综合目标函数,即针对3个目标的重要程度分别设置权重系数wz(z=1, 2, 3)。在本文的试验背景中,工务部门测试了钢轨打磨前的列车曲线动力学性能,发现轮重减载率离超限的危险程度最大,脱轨系数与轮轴横向力的危险程度次之,因此,取权重系数w1=0.3,w2=0.4,w3=0.3。同时,为统一3个目标的数量级,将式(12)进行归一化处理,则优化目标函数fv(v)可表示为
{f_{\rm{v}}}\left( \boldsymbol{v} \right) = {w_1}{f_1}\left( \boldsymbol{v} \right) + {w_2}{f_2}\left( \boldsymbol{v} \right)/0.65 + {w_3}{f_3}\left( \boldsymbol{v} \right)/35 (13) 1.3 约束方程
在钢轨优化区域内,圆弧切点坐标约束g1应满足
{g_1} = {x_{{p_5}}} < {x_{{p_4}}} < {x_{{p_3}}} < {x_{{p_2}}} < {x_{{p_1}}} (14) 钢轨打磨是去除钢轨表面材料,打磨廓形曲线高度应低于初始廓形。钢轨廓形由圆弧切点和圆弧半径计算所得,式(14)已对切点进行约束,因此,对打磨廓形的高度上限约束g2可用圆弧半径表示为
{g_2} = {R_{\rm{g}}} \le {R_{\rm{i}}} (15) 式中:Ri为钢轨初始圆弧半径;Rg为钢轨打磨廓形圆弧半径。
虽然在钢轨廓形曲线推导时,已保证各圆弧连接处的相切关系,但由于解析解与数值解存在一定计算误差δ[26],将导致计算过程中固定点p5的切线斜率kp5难以与优化曲线外侧严格相切,同时由于p5处为轮轨非接触区域,因此,以固定点p5的切线斜率约束作为打磨廓形的高度下限约束g3
{g_3} = {k_{{p_5}}} - k\left( \delta \right) < k\left( {{C_4}} \right) \le {k_{{p_5}}} (16) 式中:k(δ)为斜率允许误差;k(C4)为圆弧4在p5处的切线斜率。
由式(11)~(16)可知,优化数学模型可表示为
\left\{ {\begin{array}{*{20}{l}} {\min \;{f_{\rm{v}}}\left( \boldsymbol{v} \right) = {w_1}{f_1}\left( \boldsymbol{v} \right) + {w_2}{f_2}\left( \boldsymbol{v} \right)/0.65 + {w_3}{f_3}\left( \boldsymbol{v} \right)/35}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}.\;{g_1}, {g_2}, {g_3}} \end{array}} \right. (17) 2. 优化方法
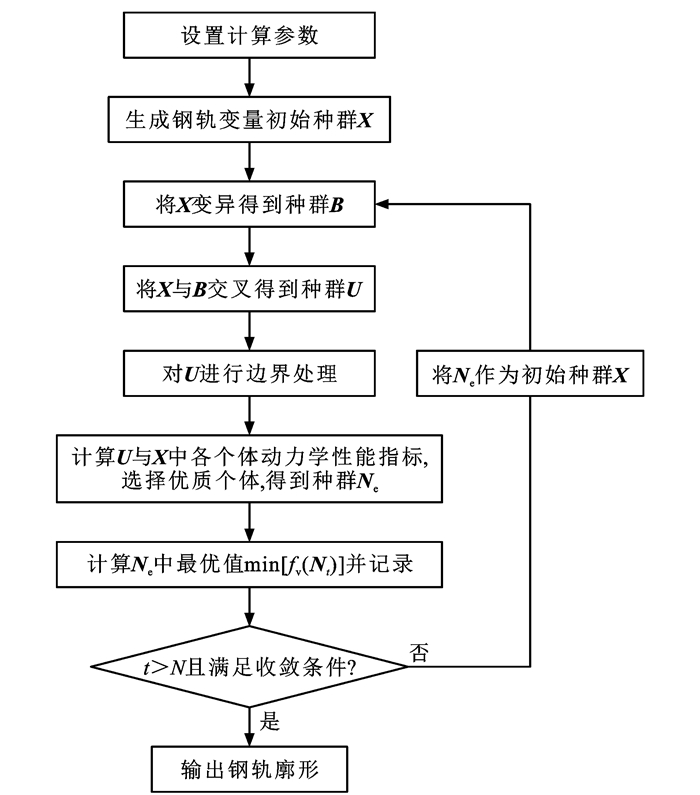
DE算法[27-28]是一种基于现代智能理论的优化算法,通过群体内个体之间的相互合作与竞争产生的群体智能来指导优化搜索的方向。该算法的基本思想是:从一个随机产生的初始种群开始,通过把种群中任意2个个体的向量差与第3个个体求和来产生新个体(变异),然后将新个体与当代种群中相应的个体相比较(交叉),如果新个体的适应度优于当前个体,则在下一代中就用新个体取代旧个体,否则仍保存旧个体(选择)。通过不断地进化,保留优良个体,淘汰劣质个体,引导搜索向最优解逼近。DE算法主要的控制参数包括种群规模N、个体长度D、缩放因子F和交叉概率因子C。其中N表示种群信息的丰富度,影响着算法计算量;D表示种群中每个向量的长度,由变量数量决定;F控制变异过程的缩放大小,对算法的寻优能力影响较大,F越大变异程度越大,但收敛速度也随之变慢;C控制父代与子代间的信息交换程度,同样也影响着种群的多样性。
在算法开始前,选定算法中各控制参数,将优化模型中的钢轨变量v以种群个体形式表达为
\boldsymbol{v} \to \boldsymbol{x} = \left( {{d_1}, {d_2}, \cdots , {d_D}} \right) (18) 式中:x为种群中个体向量;d1、d2、…、dD为v中的各变量。
种群可表示为
\boldsymbol{X} = \left( {{\boldsymbol{x}_1}, {\boldsymbol{x}_2}, \cdots , {\boldsymbol{x}_N}} \right) (19) 式中:X为一个种群,由N个个体向量x1、x2、…、xN组成。
利用DE算法设计钢轨非对称打磨廓形的过程表示如下。
首先,在约束空间内随机生成初始种群X,对初始种群的每个体向量进行变异操作,即
{\boldsymbol{b}_m} = {\boldsymbol{x}_{{r_1}}} + F\left( {{\boldsymbol{x}_{{r_2}}} - {\boldsymbol{x}_{{r_3}}}} \right) (20) 式中:bm为变异种群B中第m个个体;xr1、xr2、xr3为初始种群中随机选择的个体向量,且满足r1≠r2≠r3≠m。
获得变异种群后,通过产生随机值与交叉概率因子C和维度h(h=1, 2, …, D)的比较,对种群维度向量进行交叉,从变异种群B和初始种群X中生成交叉后的交叉种群U,且
{\boldsymbol{u}_h} = \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{b}_h}\;\;\;\;\;{\rm{rand}}\left( h \right) \le C\;或\;S\left( h \right) = h}\\ {{\boldsymbol{x}_h}\;\;\;\;\;{\rm{rand}}\left( h \right) > C\;且\;S\left( h \right) \ne h} \end{array}} \right. (21) 式中:rand(h)为对每一维度在[0, 1]中产生一个随机值;S(h)=ceil[rand(h)D],为维度序列产生的一个随机值,ceil(·)为向上取整操作;uh、bh和xh分别为交叉种群、变异种群和初始种群中维度h的列向量。
初始种群经过变异和交叉后,个体存在超出约束空间的值,此时将随机生成一个边界内的新个体,对交叉种群中的超界个体进行替换,交叉种群U得到更新。
此时,分别计算交叉种群U和初始种群X中各个个体的目标函数,选择优质个体形成新种群Ne:若交叉种群的某个体目标值优于初始种群,则将初始种群的该个体替换为交叉个体,反之保留初始个体,即
{\boldsymbol{n}_m} = \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{u}_m}\;\;\;\;{f_{\rm{v}}}\left( {{\boldsymbol{u}_m}} \right) \le {f_{\rm{v}}}\left( {{\boldsymbol{x}_m}} \right)}\\ {{\boldsymbol{x}_m}\;\;\;\;{f_{\rm{v}}}\left( {{\boldsymbol{u}_m}} \right) > {f_{\rm{v}}}\left( {{\boldsymbol{x}_m}} \right)} \end{array}} \right. (22) 式中:fv(um)和fv(xm)为种群个体的计算目标值,在本文中即为计算钢轨廓形变量所对应的动力学目标函数;nm为新种群Ne的个体。
计算种群Ne中每个个体的目标函数,取最小目标值记为min[fv(Nt)](Nt为第t次迭代的种群)。由于该问题为多目标优化问题,在进化过程中会存在连续多代个体适应性值相似的情况,同时,DE算法的收敛性也受控制参数的影响,因此,记录前N次进化值,当进化次数t>N时,给定收敛条件
\min \left[ {{f_{\rm{v}}}\left( {{\boldsymbol{N}_t}} \right)} \right] - \min \left[ {{f_{\rm{v}}}\left( {{\boldsymbol{N}_{t - N}}} \right)} \right] < \varepsilon \;或\;t = G (23) 式中:ε为允许精度;G为最大迭代次数。
若种群经过N次迭代后目标函数值满足收敛精度或达到最大迭代次数,算法终止;若不满足收敛精度则将Nt作为t+1次进化的初始种群。理论上将钢轨廓形变量通过多次进化可以获得全局最优值,即可得到钢轨非对称打磨廓形,求解流程如图 2所示。
3. 结果分析
3.1 优化结果
根据图 2所示流程对优化模型进行编程求解,形成了闭环的数值计算程序,选取相关控制参数对钢轨非对称打磨廓形进行设计,计算参数如表 2所示。
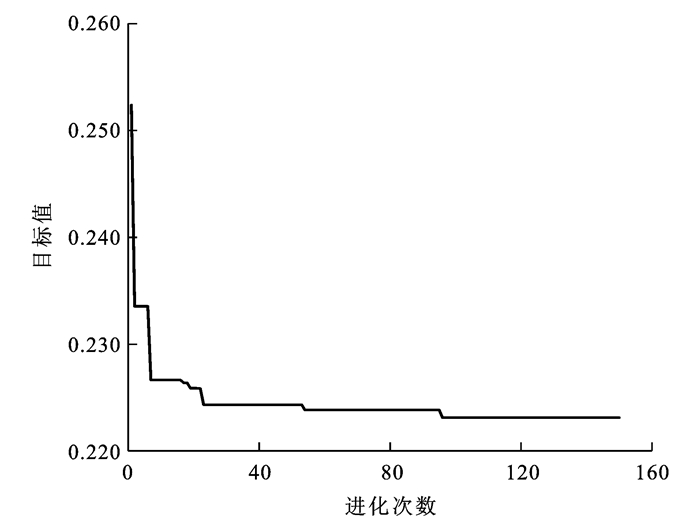
表 2 计算参数Table 2. Calculation parameters参数 数值 N 50 F 0.5 C 0.9 G 200 ε 1.0×10-5 p1 (25.330, -2.195) p5 (-35.400, -14.200) kp1 -0.232 kp5 20 图 3为优化过程的进化曲线,可见:随着进化次数的增加,目标值逐渐降低,当进化次数到达97时,目标函数已取得全局最优点,说明该方法具有较快的计算速度;在经过147次进化后算法停止,获得理想目标廓形。
图 4给出了优化所得钢轨打磨廓形与初始廓形对比,可见:优化钢轨的内外轨出现非对称现象,从钢轨打磨角度看,外轨打磨区域偏向于钢轨外侧,内轨打磨区域偏向于钢轨内侧;外轨打磨区域为-35~20 mm,在-31 mm处的最大垂向打磨量约为4.1 mm,内轨打磨区域为-35~15 mm,在-32 mm处的最大垂向打磨量约为1.6 mm;通过不同打磨区域和打磨量改变列车通过曲线时轮对的接触位置,获得较大的轮径差,以提高其曲线通过性能。
3.2 轮轨接触几何状态
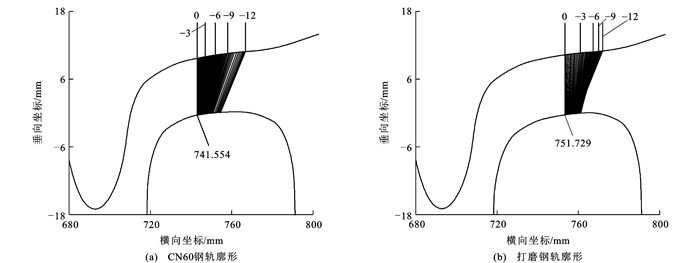
图 5、6分别给出了优化前后内外钢轨与LM车轮踏面匹配的轮轨接触点分布状态,可见:钢轨打磨使外轨对中位置接触点由打磨前的-741.554 mm向轨道内侧移动了约9 mm,至-732.232 mm处,内轨对中位置由741.554 mm向轨道外侧移动了约10 mm,至751.729 mm处;同时,打磨廓形并未改变外轨轮缘处的匹配特性,保证了轮轨不会因对中位置改变而过早发生轮缘贴靠现象。这种接触特性使列车进入曲线时可获得较大的轮径差,以提升曲线通过性能。
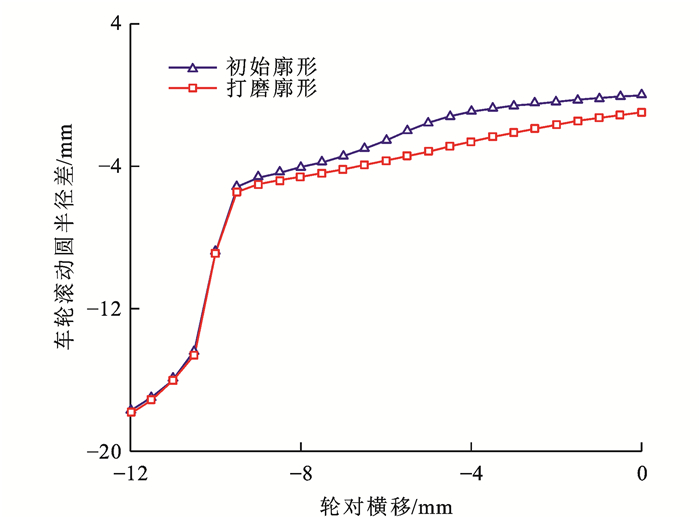
图 7给出了轮对横移12 mm范围内的车轮滚动圆半径差变化曲线,可见:优化钢轨使轮对横移在0~10 mm范围内的轮径差有所增大,这有助于提升列车的曲线通过性能。
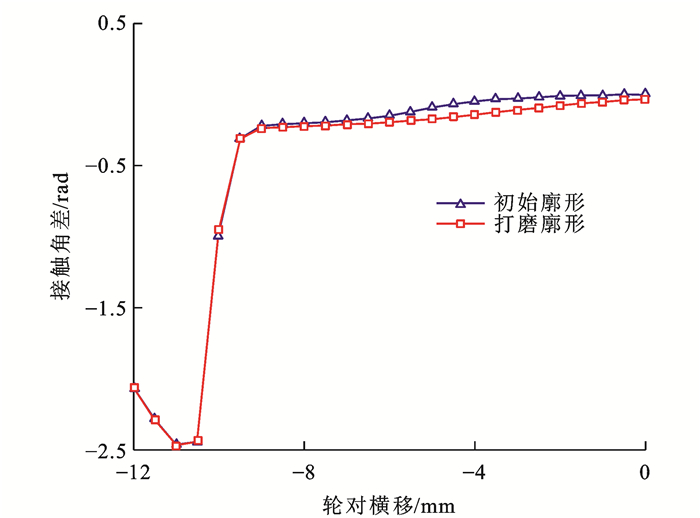
轮轨接触角[29]为轮轨接触点公切面与轮对轴线间的夹角,当轮对通过曲线时向曲线外侧发生横移将产生接触角差,图 8给出了钢轨打磨前后轮轨接触角差对比,可见:钢轨打磨提高了轮对横移0~10 mm范围内的接触角差,接触角差的提高使车轮与外轨顶面接触时法向力的横向分力提供了一定的轮对导向力,降低了轮缘与钢轨侧面的接触概率,在一定程度上提高了列车曲线通过能力。
3.3 曲线通过性能
施加美国五级谱作为线路随机不平顺激励,采用表 1所示仿真参数对钢轨打磨前后的列车曲线通过性能进行了验证。图 9为列车通过曲线时的轮对横移响应。列车以90 km·h-1通过该曲线线路时存在欠超高现象,轮对会向曲线外轨侧发生横移,增大轮轨横向力及列车倾覆的危险性。由图 9可以看出:钢轨打磨后轮对横移较打磨前有所下降,这和打磨后较大的轮径差有关,与轮轨接触状态分析的结论一致。
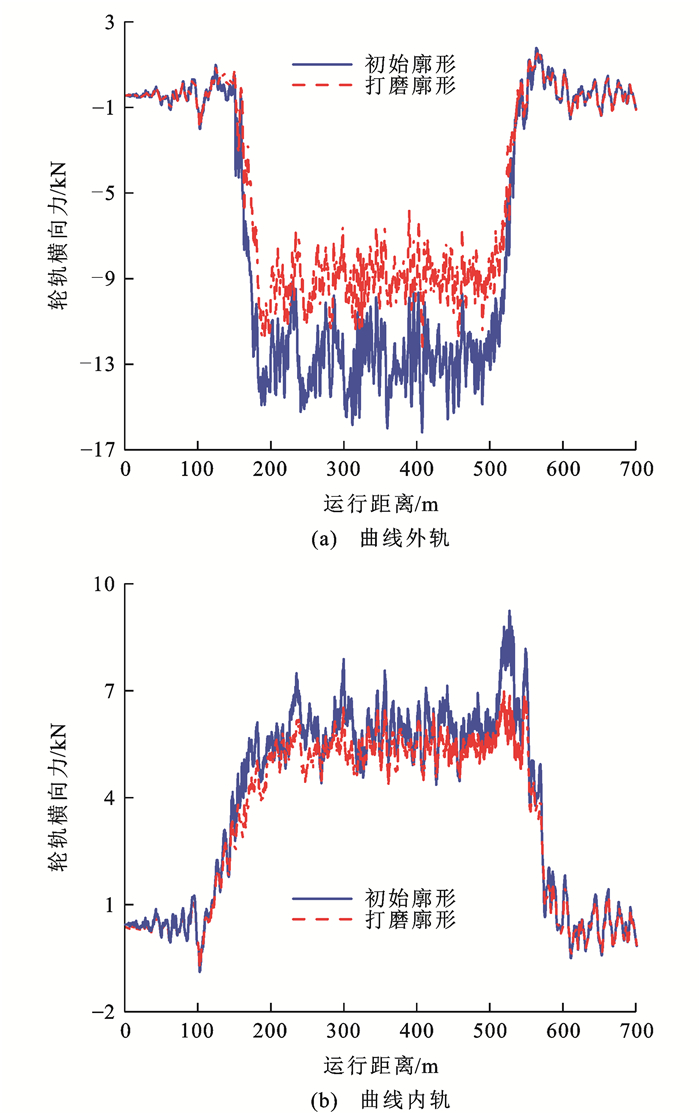
图 10给出了列车通过曲线时的轮轨横向力响应,可见:打磨钢轨使曲线外侧轮轨横向力明显降低,横向力均值由打磨前的12.85 kN降低为9.06 kN,降低幅度为29.4%;曲线内侧钢轨横向力也略有降低,其降低幅度为8.3%;轮轨横向力的下降导致内外钢轨的脱轨系数得以降低,有利于提高列车的运行安全性(图 11)。
为评估打磨前后提速货物列车通过曲线时的倾覆性能,图 12给出了钢轨打磨前后列车的轮重减载率,可见:钢轨打磨通过增大轮径差均衡了小半径曲线上列车轮对的左右轮重,轮重减载率降低约22.05%。
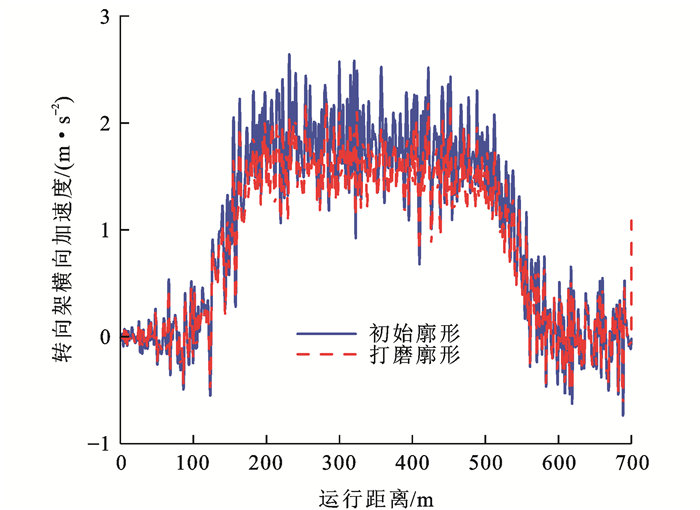
对侧架横向振动加速度进行0.5~10 Hz带通滤波处理,对滤波后的时域振动波形进行评估,若波形中出现连续6次达到或超过8 m·s-2时,判定转向架失稳。列车通过曲线时转向架横向振动加速度如图 13所示,钢轨打磨前后列车转向架均未出现失稳情况,但从结果来看,钢轨打磨仍然提高了转向架的横向稳定性。
图 14给出了列车通过曲线时的轮轨磨耗指数与运行距离的变化曲线,由于打磨钢轨使得列车曲线通过性能得到提升,改善了轮轨的蠕滑状态,使轮轨间蠕滑力与蠕滑率有所下降,降低了左右轮轨的磨耗指数。
图 15、16分别给出了钢轨打磨前后列车通过小半径曲线时的轮轨接触斑面积和轮轨最大接触应力。由于钢轨打磨改变了轮轨接触区域的钢轨廓形曲率,且由图 6可以看出内轨的轮轨接触点在钢轨上较为集中,这导致打磨钢轨接触斑面积减小(图 15),轮轨接触应力提高(图 16)。轮轨接触应力的提高易导致轮轨发生塑性变形,故需对此进行计算分析。目前常用安定极限qm衡量轮轨最大接触应力的许可范围,其可表示为[30]
{q_{\rm{m}}} \le \frac{4}{{\sqrt 3 }}{\sigma _{\rm{s}}} (24) 式中:σs为钢轨屈服强度。
取钢轨屈服强度为650 MPa[31],算得安定极限为1 501 MPa。由图 15、16可知:打磨前曲线外侧轮轨接触应力显著大于内侧轮轨接触应力;虽然打磨后的曲线外侧轮轨接触斑面积有所降低,但由图 11可知,打磨钢轨降低了列车向外轨侧倾覆的风险,外轨侧增载现象得到缓解,轮轨接触应力保持与打磨前一致;曲线内侧轮轨接触斑明显减小,导致轮轨接触应力大幅提升,达到和外轨侧相近的水平;总体看,内外轨最大接触应力均处于安定极限以内,满足铁路轮轨强度要求。
对比分析钢轨打磨前后列车通过圆曲线时的各性能指标,其平均值如表 3所示。打磨钢轨使列车通过曲线时的动力学性能和磨耗性能得到有效改善,其中轮对横移、轮重减载率和转向架横向加速度分别降低了7.70%、22.05%和12.20%;外轨横向力、外轨脱轨系数和外轨磨耗指数分别减小了29.40%、27.30%和12.30%;内轨横向力、内轨脱轨系数和内轨磨耗指数也分别减小了8.30%、7.70%和7.90%。采用钢轨非对称打磨使内外钢轨的接触斑面积分别减小了30.80%和5.70%,最大接触应力分别增大了52.40%和0.91%,但并未使轮轨材料超过安定极限。
表 3 曲线通过性能验证结果Table 3. Verification result of curve passing performance性能指标 打磨前均值 打磨后均值 提升率/% 轮对横移/mm 9.85 9.09 -7.70 轮重减载率 0.322 0.251 -22.05 转向架横向加速度/(m·s-2) 1.794 1.575 -12.20 外轨横向力/kN 12.85 9.06 -29.40 外轨脱轨系数 0.337 0.245 -27.30 外轨磨耗指数 95.85 84.05 -12.30 外轨接触斑面积/mm2 60.73 56.90 -5.70 外轨接触应力/MPa 955.57 964.34 0.91 内轨横向力/kN 5.87 5.38 -8.30 内轨脱轨系数 0.245 0.226 -7.70 内轨磨耗指数 63.465 58.413 -7.90 内轨接触斑面积/mm2 61.27 42.36 -30.80 内轨接触应力/MPa 597.28 910.16 52.40 4. 结语
(1) 以钢轨廓形的圆弧半径及切点坐标作为设计变量,对钢轨廓形进行了几何推导,获得了廓形的解析表达式。运用建立的列车系统多刚体动力学模型获取了车辆动力学性能指标,作为优化设计的综合目标函数,提出了一种小半径曲线钢轨非对称打磨廓形优化数学模型。基于差分进化算法编写了数值求解程序,对优化模型进行了求解,计算结果表明该方法具有较快的计算速度,可获得理想的钢轨打磨廓形。
(2) 获得的内外钢轨廓形具有不同的打磨范围及打磨量,这种非对称打磨廓形可为列车进入曲线后提供较大轮径差和轮轨接触角差,有助于提升列车曲线通过性能。
(3) 经理论验证,打磨后钢轨廓形可有效减小轮对横移,降低轮轨横向力、脱轨系数和轮重减载率,提高了转向架曲线横向稳定性,降低了轮轨磨耗。虽然钢轨打磨造成轮轨接触应力增大,但并不会使轮轨发生塑性变形。
(4) 本文仅针对列车曲线通过性能进行钢轨非对称打磨廓形设计,尚未考虑钢轨材料去除量等因素,在下一步研究中,将结合钢轨打磨工艺改进方法的经济性。
-
表 1 小半径曲线仿真参数
Table 1. Simulation parameters of sharp curve
参数 数值 两端直线长度/m 100 两端缓和曲线长度/m 100 曲线半径/m 800 曲线长度/m 300 线路超高/mm 100 采样频率/Hz 200 运行速度/(km·h-1) 90 表 2 计算参数
Table 2. Calculation parameters
参数 数值 N 50 F 0.5 C 0.9 G 200 ε 1.0×10-5 p1 (25.330, -2.195) p5 (-35.400, -14.200) kp1 -0.232 kp5 20 表 3 曲线通过性能验证结果
Table 3. Verification result of curve passing performance
性能指标 打磨前均值 打磨后均值 提升率/% 轮对横移/mm 9.85 9.09 -7.70 轮重减载率 0.322 0.251 -22.05 转向架横向加速度/(m·s-2) 1.794 1.575 -12.20 外轨横向力/kN 12.85 9.06 -29.40 外轨脱轨系数 0.337 0.245 -27.30 外轨磨耗指数 95.85 84.05 -12.30 外轨接触斑面积/mm2 60.73 56.90 -5.70 外轨接触应力/MPa 955.57 964.34 0.91 内轨横向力/kN 5.87 5.38 -8.30 内轨脱轨系数 0.245 0.226 -7.70 内轨磨耗指数 63.465 58.413 -7.90 内轨接触斑面积/mm2 61.27 42.36 -30.80 内轨接触应力/MPa 597.28 910.16 52.40 -
[1] 彭敬康, 崔大宾, 付耀东, 等. 提速货物列车车轮凹磨限值研究[J]. 铁道科学与工程学报, 2022, 19(2): 511-519. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202202025.htmPENG Jing-kang, CUI Da-bin, FU Yao-dong, et al. Research on hollow-worn limit of wheel treads of freight trains subjected to speed increase[J]. Journal of Railway Science and Engineering, 2022, 19(2): 511-519. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202202025.htm [2] 王璐颖. 钢轨打磨车抗脱轨稳定性研究[D]. 成都: 西南交通大学, 2012.WANG Lu-ying. Research on anti-derailment of rail grinding train[D]. Chengdu: Southwest Jiaotong University, 2012. (in Chinese) [3] 傅荧. 我国铁路货运市场占有率现状分析及展望[J]. 四川教育学院学报, 2002(7): 56-59. doi: 10.3969/j.issn.1000-5757.2002.07.023FU Ying. Analysis and prospect of railway freight market share in China[J]. Journal of Sichuan College of Education, 2002(7): 56-59. (in Chinese) doi: 10.3969/j.issn.1000-5757.2002.07.023 [4] 田生奎. 中国铁路货运市场现状及发展战略研究[D]. 北京: 对外经济贸易大学, 2007.TIAN Sheng-kui. Research on current situation and development strategy of railway freight market in China[D]. Beijing: University of International Business and Economics, 2007. (in Chinese) [5] 卢军. 钢轨打磨列车打磨质量控制[J]. 铁道技术监督, 2011, 39(1): 26-28. doi: 10.3969/j.issn.1006-9178.2011.01.011LU Jun. Grinding quality control of rail grinding train[J]. Railway Quality Control, 2011, 39(1): 26-28. (in Chinese) doi: 10.3969/j.issn.1006-9178.2011.01.011 [6] 杨国伟, 魏宇杰, 赵桂林, 等. 高速列车的关键力学问题[J]. 力学进展, 2015, 45: 217-460. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201500007.htmYANG Guo-wei, WEI Yu-jie, ZHAO Gui-lin, et al. Research progress on the mechanics of high speed rails[J]. Advances in Mechanics, 2015, 45: 217-460. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201500007.htm [7] 温士明. 地铁线路小半径曲线钢轨打磨廓形研究[D]. 成都: 西南交通大学, 2018.WEN Shi-ming. Study on rail grinding profile for small radius curved track of metro line[D]. Chengdu: Southwest Jiaotong University, 2018. (in Chinese) [8] 周清跃, 田常海, 张银花, 等. 高速铁路钢轨打磨关键技术研究[J]. 中国铁道科学, 2012, 33(2): 66-70. doi: 10.3969/j.issn.1001-4632.2012.02.12ZHOU Qing-yue, TIAN Chang-hai, ZHANG Yin-hua, et al. Research on key rail grinding technology of high-speed railway[J]. China Railway Science, 2012, 33(2): 66-70. (in Chinese) doi: 10.3969/j.issn.1001-4632.2012.02.12 [9] MAGEL E, RONEY M, KALOUSEK J, et al. The blending of theory and practice in modern rail grinding[J]. Fatigue and Fracture of Engineering Materials and Structures, 2003, 26(10): 921-929. doi: 10.1046/j.1460-2695.2003.00669.x [10] 贺振中. 国外钢轨打磨技术的应用与思考[J]. 中国铁路, 2000(10): 38-40. doi: 10.3969/j.issn.1001-683X.2000.10.014HE Zhen-zhong. Application and thinking of rail grinding technology abroad[J]. China Railway, 2000(10): 38-40. (in Chinese) doi: 10.3969/j.issn.1001-683X.2000.10.014 [11] MARICH S. Rail grinding strategies adopted in Australia[J]. Rail Engineering International Edition, 2005, 34(1): 4-6. [12] 郭俊. 轮轨滚动接触疲劳损伤机理研究[D]. 成都: 西南交通大学, 2006.GUO Jun. Study on mechanism of wheel-rail rolling contact fatigue and damage[D]. Chengdu: Southwest Jiaotong University, 2006. (in Chinese) [13] 郭俊, 刘启跃, 王文健. 钢轨打磨对轮轨滚动接触斑行为影响研究[J]. 铁道建筑, 2009, 49(12): 92-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200912034.htmGUO Jun, LIU Qi-yue, WANG Wen-jian. Research on influence of rail grinding on wheel-rail rolling contact spot behavior[J]. Railway Engineering, 2009, 49(12): 92-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200912034.htm [14] SMALLWOOD R, SINCLAIR J C, SAWLEY K J. An optimization technique to minimize rail contact stresses[J]. Wear, 1991, 144(1/2): 373-384. [15] MAGEL E, KALOUSEK J. Designing and assessing wheel/rail profiles for improved rolling contact fatigue and wear performance[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail Rapid Transit, 2017, 231(7): 805-818. doi: 10.1177/0954409717708079 [16] MAGEL E E, KALOUSEK J. The application of contact mechanics to rail profile design and rail grinding[J]. Wear, 2002, 253(1/2): 308-316. [17] 崔大宾, 李立, 金学松, 等. 铁路钢轨打磨目标型面研究[J]. 工程力学, 2011, 28(4): 178-184. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201104030.htmCUI Da-bin, LI Li, JIN Xue-song, et al. Study on rail goal profile by grinding[J]. Engineering Mechanics, 2011, 28(4): 178-184. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201104030.htm [18] 崔大宾, 李立, 金学松, 等. 基于轮轨法向间隙的车轮踏面优化方法[J]. 机械工程学报, 2009, 45(12): 205-211. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200912038.htmCUI Da-bin, LI Li, JIN Xue-song, et al. Numerical optimization technique for wheel profile considering the normal gap of the wheel and rail[J]. Journal of Mechanical Engineering, 2009, 45(12): 205-211. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200912038.htm [19] 崔大宾, 李立, 金学松. 重载货车车轮踏面优化研究[J]. 铁道学报, 2011, 33(5): 31-37. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201105010.htmCUI Da-bin, LI Li, JIN Xue-song. Study on optimization of wheel profiles on heavy haul freight car[J]. Journal of the China Railway Society, 2011, 33(5): 31-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201105010.htm [20] ZHAI Wan-ming, GAO Jian-min, LIU Peng-fei, et al. Reducing rail side wear on heavy-haul railway curves based on wheel-rail dynamic interaction[J]. Vehicle System Dynamics, 2014, 52(S1): 440-454. [21] 毛鑫, 沈钢. 基于轮径差函数的曲线钢轨打磨廓形设计[J]. 同济大学学报(自然科学版), 2018, 46(2): 253-259. doi: 10.11908/j.issn.0253-374x.2018.02.017MAO Xin, SHEN Gang. Curved rail grinding profile design based on rolling radii difference function[J]. Journal of Tongji University (Natural Science), 2018, 46(2): 253-259. (in Chinese) doi: 10.11908/j.issn.0253-374x.2018.02.017 [22] 陈步琛, 沈钢. 基于平均踏面廓形的动力学最优钢轨廓形设计[J]. 齐齐哈尔大学学报(自然科学版), 2019, 35(4): 30-35. https://www.cnki.com.cn/Article/CJFDTOTAL-QQHE201904008.htmCHEN Bu-chen, SHEN Gang. Optimized design of rail profile based on mean tread profile[J]. Journal of Qiqihar University (Natural Science Edition), 2019, 35(4): 30-35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QQHE201904008.htm [23] 林凤涛, 吴涛, 杨洋, 等. 高速铁路辙叉区钢轨打磨廓形设计方法[J]. 交通运输工程学报, 2021, 21(6): 124-135. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202106009.htmLIN Feng-tao, WU Tao, YANG Yang, et al. Design method of rail grinding profile in frog area of high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2021, 21(6): 124-135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202106009.htm [24] 林凤涛, 胡伟豪. 磨耗钢轨经济性打磨型面研究[J]. 铁道科学与工程学报, 2020, 17(10): 2493-2502. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202010007.htmLIN Feng-tao, HU Wei-hao. Study on the economical grinding surface of wear rail[J]. Journal of Railway Science and Engineering, 2020, 17(10): 2493-2502. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202010007.htm [25] 林凤涛, 庞华飞, 邓卓鑫, 等. 曲线区钢轨双打磨廓形设计方法[J]. 铁道科学与工程学报, 2022, 19(1): 87-99. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202201011.htmLIN Feng-tao, PANG Hua-fei, DENG Zhuo-xin, et al. Design method of double grinding profile for curved rail[J]. Journal of Railway Science and Engineering, 2022, 19(1): 87-99. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD202201011.htm [26] VERMA K A, PANDEY K M, RAY M, et al. The numerical analysis of combustion performance of a wedge shaped strut-based scramjet combustor[J]. Thermal Science and Engineering Progress, 2020, 20: 10074. [27] HASSAN S, HEMEIDA A M, ALKHALAF S, et al. Multi-variant differential evolution algorithm for feature selection[J]. Scientific Reports, 2020, 10(1): 17261. [28] YU Xiao-bing, LI Chen-liang, ZHOU Jia-fang. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios[J]. Knowledge-Based Systems, 2020, 204: 106209. [29] ZHANG Zhi-bo, WU Ping-bo, LUO Ren, et al. The relationship between contact angle difference and equivalent conicity of high-speed EMU[J]. Advanced Materials Research, 2012, 591/592/593: 1920-1924. [30] 刘启跃. 钢轨的安定状态研究[J]. 西南交通大学学报, 1995, 30(4): 466-471. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT504.019.htmLIU Qi-yue. The study of shakedown of rail[J]. Journal of Southwest Jiaotong University, 1995, 30(4): 466-471. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT504.019.htm [31] 张银花, 陈朝阳, 周清跃. 钢轨屈服强度指标取值研究[J]. 铁道建筑, 2006, 46(3): 92-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200603035.htmZHANG Yin-hua, CHEN Chao-yang, ZHOU Qing-yue. Research on the value of yield strength index of rail[J]. Railway Engineering, 2006, 46(3): 92-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200603035.htm 期刊类型引用(5)
1. 张翼. 个性化设计廓形打磨钢轨在高速铁路小半径曲线波磨病害整治中的应用. 铁道技术监督. 2024(01): 42-47 .  百度学术
百度学术2. 梁仲玺. 钢轨廓形打磨在小半径曲线下股轨顶疲劳掉块病害整治中的应用. 铁路采购与物流. 2024(07): 56-58 .  百度学术
百度学术3. 周骏,刘林芽,李纪阳. 基于多目标优化策略的曲线钢轨非对称打磨设计. 铁道科学与工程学报. 2024(08): 3166-3178 .  百度学术
百度学术4. 李伟. 道岔钢轨打磨对轮轨动力学影响分析. 机电信息. 2023(01): 66-68 .  百度学术
百度学术5. 张斌,汪龙洋,杨宗超,孙奇,万文超,汤金伟. 小半径曲线段钢轨打磨方案比选及动力特性研究. 振动与冲击. 2023(24): 169-174+184 .  百度学术
百度学术其他类型引用(2)
-






 下载:
下载:















 下载:
下载:








 百度学术
百度学术
















