整体式斜交桥中桥台钢桩地震响应

赵秋红; 郭浩猛; 董硕; 王晴薇; 陈宝春; 周勇军

doi:10.19818/j.cnki.1671-1637.2022.05.006

整体式斜交桥中桥台钢桩地震响应

doi: 10.19818/j.cnki.1671-1637.2022.05.006

赵秋红^{1, 2,},
郭浩猛¹,
董硕³,
王晴薇⁴,
陈宝春⁵,
周勇军^6, ,

1.
天津大学建筑工程学院，天津 300350
2.
天津大学滨海土木工程结构与安全教育部重点实验室，天津 300350
3.
山东科技大学山东省土木工程防灾减灾重点实验室，山东青岛 266590
4.
北京构力科技有限公司，北京 100013
5.
福州大学土木工程学院，福建福州 350116
6.
长安大学公路大型结构安全教育部工程研究中心，陕西西安 710064

基金项目:

国家自然科学基金项目 51878447

国家自然科学基金项目 51678406

中央高校基本科研业务费专项资金项目 300102212524

详细信息

作者简介:
赵秋红(1975-)，女，湖北宜昌人，天津大学副教授，工学博士，从事桥梁抗震、高性能结构及材料研究

通讯作者:
周勇军(1978-)，男，湖北孝昌人，长安大学教授，工学博士

中图分类号: U443.15
计量
- 文章访问数: 371
- HTML全文浏览量: 115
- PDF下载量: 62
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-31
- 刊出日期: 2022-10-25

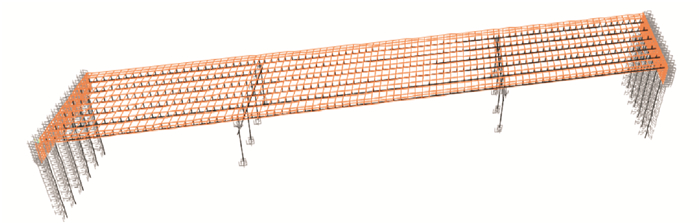
Seismic responses of abutment steel piles in integral skewed bridges

1.
School of Civil Engineering, Tianjin University, Tianjin 300350, China
2.
Key Laboratory of Coast Civil Structure Safety of Ministry of Education, Tianjin University, Tianjin 300350, China
3.
Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation, Shandong University of Science and Technology, Qingdao 266590, Shandong, China
4.
Beijing Glory PKPM Technology Co., Ltd., Beijing 100013, China
5.
College of Civil Engineering, Fuzhou University, Fuzhou 350116, Fujian, China
6.
Research Center of Highway Large Structure Engineerin on Safety, Ministry of Education, Chang'an University, Xi'an 710064, Shaanxi, China

Funds:

National Natural Science Foundation of China 51878447

National Natural Science Foundation of China 51678406

Fundamental Research Funds for the Central Universities 300102212524

More Information

Author Bio:
ZHAO Qiu-hong (1975–), female, born in Yichang, Hubei Province, associate professor at Tianjin University, PhD. She is mainly engaged in research on earthquake resistance and high-performance structures and materials of bridges. E-mail: qzhao@tju.edu.cn

ZHOU Yong-jun (1978–), male, born in Xiaochang, Hubei Province, PhD, professor at Chang'an University. E-mail: zyj@chd.edu.cn

摘要

摘要: 采用有限元分析软件SAP2000建立了某整体式斜交桥的三维结构模型，通过离散非线性弹簧单元模拟桥台-台后土以及H型钢桩-桩周土的土-结构相互作用，通过一系列双向地震作用下的非线性时程分析，研究了桩的朝向、桩周土刚度及桩头转动刚度对整体式斜交桥中H型钢桩地震响应的影响规律。研究结果表明：双向地震作用下，H型钢桩的横桥向位移显著大于纵桥向，且受桩朝向的影响更为明显，强、弱轴弯矩均呈正反双向分布，屈服面函数最大值一般位于桩顶，另一峰值则位于桩身2~4 m埋深处；钢桩绕强轴弯曲布置时，桩顶纵桥向位移相比绕弱轴弯曲时降低18.2%，但横桥向位移增大47.7%，桩顶处绕强轴弯矩增加约3.9倍，桩身反向强轴弯矩峰值降低67.0%，桩顶处绕弱轴弯矩基本不变，桩身反向弱轴弯矩峰值增加约1.0倍；随着桩周土刚度的降低，桩顶纵、横桥向位移增大，桩顶屈服面函数值降低，而桩身屈服面函数峰值增加，桩身更不易保持弹性；当桩头采用柔性连接时，桩顶纵、横桥向位移均增大，桩顶屈服面函数值降低，有利于保护桩头，而桩身屈服面函数峰值增加，当桩头转动刚度过低时甚至可能大于桩顶刚度，导致桩身在罕遇地震作用下先进入塑性。
- 桥梁工程 /
- 整体式斜交桥 /
- 非线性时程分析 /
- H型钢桩 /
- 桩的朝向 /
- 桩周土刚度 /
- 桩头转动刚度
Abstract: A three-dimensional structural model of a integral skewed bridge was established by using finite element analysis software SAP2000, and the interactions of abutment-soil behind the abutment and H-shaped steel pile-soil around the pile were simulated through a discrete nonlinear spring element. Through nonlinear time-history analysis under a series of bi-directional seismic actions, the influence rules of pile orientation, stiffness of the soil around the pile, and rotational stiffness of pile head on the seismic responses of the H-shaped steel pile in the skewed integral abutment bridge were studied. Research results show that under bi-directional seismic actions, the transverse displacement of the H-shaped steel pile is significantly greater than the longitudinal displacement, and greatly affected by the pile orientation. The bending moments around the strong and weak axes distribute in both positive and negative directions. The maximum values of yield surface function are generally located at the pile top, while the other peak values are located at the 2-4 m where the pile body is buried. When the steel pile is arranged around strong axis bending, the longitudinal displacement at the pile top reduces by 18.2% compared with that around weak axis bending, but the transverse displacement increases by 47.7%. The bending moment around the strong axis at the pile top increases by about 3.9 times, while the bending moment peak value of reverse strong axis of the pile body decreases by about 67.0%. The bending moment around the weak axis at the pile top basically unchanges, while the bending moment peak value around the reverse weak axis of the pile body increases by about 1.0 times. With the decrease in the stiffness of the soil around the pile, the longitudinal and transverse displacements at the pile top improve, and the yield surface function value at the pile top reduces slightly, while the peak value of the yield surface function of the pile body increases. The pile body is difficult to be elastic. When a flexible connection is adopted at the pile head, the longitudinal and transverse displacements at the pile top both rise. The yield surface function value at the pile top decreases, and the pile head can be protected effectively, but the peak value of the yield surface function of the pile body increases. When the rotational stiffness of the pile head is too low, the peak value of the yield surface function of the pile body may be higher than the value at the pile top, and thus the pile body may enter the plastic stage first under rare earthquakes.
- bridge engineering /
- integral skewed bridge /
- nonlinear time-history analysis /
- H-shaped steel pile /
- pile orientation /
- stiffness of soil around pile /
- rotational stiffness of pile head

HTML全文

图 1 整体式斜交桥有限元模型

Figure 1. Finite element model of integral skewed bridge

下载: 全尺寸图片幻灯片

图 2 有限元模型

Figure 2. Finite element models

下载: 全尺寸图片幻灯片

图 3 台后土弹簧力-位移曲线

Figure 3. Force-displacement curves of abutment soil springs

下载: 全尺寸图片幻灯片

图 4 桩周土弹簧力-位移曲线

Figure 4. Spring force-displacement curves of soil around pile

下载: 全尺寸图片幻灯片

图 5 H型钢桩的截面弯矩-曲率曲线

Figure 5. Moment-curvature curves of H-shaped steel pile

下载: 全尺寸图片幻灯片

图 6 整体式斜交桥H型钢桩朝向

Figure 6. Orientations of H-shaped steel pile of integral skewed bridge

下载: 全尺寸图片幻灯片

图 7 桩头包裹橡胶板的桥台-H型钢桩柔性连接节点^[22]

Figure 7. Abutment-H-shaped steel pile flexible joint for pile head with rubber plate

下载: 全尺寸图片幻灯片

图 8 桥台-H型钢桩柔性连接节点的有限元模型

Figure 8. Finite element model of flexible joint of abutment-H-shaped steel pile

下载: 全尺寸图片幻灯片

图 9 骨架曲线的对比

Figure 9. Comparison of skeleton curves

下载: 全尺寸图片幻灯片

图 10 峰值加速度调整为0.6g的El-Centro、Taft及Lan1地震波记录

Figure 10. El-Centro, Taft and Lan1 seismic wave records with peak acceleration adjusted to 0.6g

下载: 全尺寸图片幻灯片

图 11 不同H型钢桩朝向的桩顶位移时程曲线

Figure 11. Displacement time-history curves of tops of H-shaped steel piles with different orientations

下载: 全尺寸图片幻灯片

图 12 不同H型钢桩朝向的桩身位移、弯矩及屈服面函数值分布

Figure 12. Distributions of displacements, moments and yield surface function values of H-shaped steel pile bodies with different orientations

下载: 全尺寸图片幻灯片

图 13 不同桩周土刚度下H型钢桩的桩身位移、弯矩及屈服面函数值分布

Figure 13. Distributions of displacements, moments and yield surface function values of H-shaped steel pile bodies with different soil stiffnesses around piles

下载: 全尺寸图片幻灯片

图 14 不同桩头转动刚度下桩身位移分布与桩顶位移曲线

Figure 14. Distributions of pile body displacements and curves of pile top displacements with different rotational stiffnesses of pile heads

下载: 全尺寸图片幻灯片

图 15 不同桩头转动刚度下H型钢桩的弯矩与屈服面函数值分布

Figure 15. Distributions of moments and yield surface function values of H-shaped steel pile with different rotational stiffnesses of pile heads

下载: 全尺寸图片幻灯片

表 1 桥梁基本信息

Table 1. Basic information of bridge

上部结构	主梁高/m		1.09
	主梁中心距/m		2.21
	桥面板厚度/m		0.21
桥台	高×厚/m		2.50×0.76
	台后密实砂土	内摩擦角/(°)	39
	台后密实砂土	容重/(kN·m^-3)	16.20
桩基础	截面型号		HP 12×84
	桩周密实砂土	内摩擦角/(°)	35
	桩周密实砂土	容重/(kN·m^-3)	19.20
橡胶支座	型号		GJZ 350×600×99

下载: 导出CSV

表 2 桥梁有限元分析模型

Table 2. Finite element analysis models of bridge

编号	桩的朝向	桩周土	桩头转动刚度/(kN·m·rad^-1)
编号	桩的朝向	桩周土	强轴	弱轴
M-1	沿桥梁轴线绕弱轴	密实	0(铰接)
M-2			1.00×10²	2.86×10¹
M-3			1.00×10³	2.86×10²
M-4			1.00×10⁴	2.86×10³
M-5			8.52×10⁴(贴橡胶板)	2.31×10⁴(贴橡胶板)
M-6			1.00×10⁵	2.86×10⁴
M-7			5.00×10⁵	1.43×10⁵
M-8			1.00×10⁶	2.86×10⁵
M-9	沿桥梁轴线绕弱轴	密实	∞(刚接)
M-10	沿桥台法线绕弱轴
M-11	沿桥梁轴线绕强轴
M-12	沿桥台法线绕强轴
M-13	沿桥梁轴线绕弱轴	松散
M-14	沿桥台法线绕弱轴	松散

下载: 导出CSV

表 3 不同桩朝向时H型钢桩的地震响应

Table 3. Seismic response of H-shaped steel piles with different orientations

模型编号	钢桩朝向	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	强轴弯矩M₁/(kN·m)		弱轴弯矩M₂/(kN·m)		屈服面函数值φ
模型编号	钢桩朝向	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	M₁₊	M_1－	M₂₊	M_2－	φ₊	φ_－
M-9	沿桥梁轴线绕弱轴	37.4	102.8	73.3	589.3	325.7	136.7	1.15	0.91
M-11	沿桥梁轴线绕强轴	30.6	151.8	358.2	194.5	313.8	276.4	1.35	1.03
M-10	沿桥台法线绕弱轴	33.2	100.9	91.0	636.7	325.8	83.9	1.15	0.98
M-12	沿桥台法线绕强轴	35.1	139.5	269.2	162.8	303.2	270.8	1.16	0.90

下载: 导出CSV

表 4 不同桩周土刚度下H型钢桩的地震响应

Table 4. Seismic responses of H-shaped steel piles with different soil stiffnesses around piles

模型编号	钢桩朝向	桩周土	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	强轴弯矩M₁/(kN·m)		弱轴弯矩M₂/(kN·m)		屈服面函数值φ
模型编号	钢桩朝向	桩周土	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	M₁₊	M_1－	M₂₊	M_2－	φ₊	φ_－
M-9	沿桥梁轴线绕弱轴	密实	37.4	102.8	73.3	589.3	325.7	136.7	1.15	0.91
M-13	沿桥梁轴线绕弱轴	松散	42.7	123.2	87.6	601.2	319.9	121.1	1.12	0.95
M-10	沿桥台法线绕弱轴	密实	33.2	100.9	91.0	636.7	325.8	83.9	1.15	0.98
M-14	沿桥台法线绕弱轴	松散	40.4	117.0	103.0	660.7	321.0	75.4	1.12	1.00

下载: 导出CSV

表 5 不同桩头转动刚度下H型钢桩的地震响应

Table 5. Seismic responses of H-shaped steel piles with different rotational stiffnesses of pile heads

模型编号	桩头强轴转动刚度/(kN·m·rad^-1)	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	强轴弯矩M₁/(kN·m)		弱轴弯矩M₂/(kN·m)		屈服面函数值φ
模型编号	桩头强轴转动刚度/(kN·m·rad^-1)	桩顶纵桥向位移/mm	桩顶横桥向位移/mm	M₁₊	M_1－	M₂₊	M_2－	φ₊	φ_－
M-1	0(铰接)	43.1	137.8	0	657.8	0	201.4	0.000	0.995
M-2	1.00×10²	43.0	144.1	6.3	666.4	0.6	205.5	0.001	1.022
M-3	1.00×10³	43.2	143.9	57.1	665.8	6.0	194.0	0.020	1.022
M-4	1.00×10⁴	48.5	135.2	107.6	669.1	113.6	185.3	0.258	1.045
M-5	8.52×10⁴(贴橡胶板)	44.0	107.9	104.1	606.5	222.1	159.2	0.647	0.929
M-6	1.00×10⁵	43.2	108.6	104.2	605.0	252.0	166.4	0.781	0.930
M-7	5.00×10⁵	41.3	106.8	102.7	602.7	313.1	164.1	1.088	0.919
M-8	1.00×10⁶	37.9	105.9	103.1	600.4	325.7	159.3	1.153	0.925
M-9	∞(刚接)	37.4	102.8	102.9	589.3	325.7	152.8	1.153	0.909

下载: 导出CSV

参考文献(30)

[1]	卢明奇, 杨庆山, 李英勇. 斜度对斜交桥地震作用下的扭转效应影响[J]. 哈尔滨工程大学学报, 2012, 33(2): 155-159. doi: 10.3969/j.issn.1006-7043.201010032 LU Ming-qi, YANG Qing-shan, LI Ying-yong. Torsion effects of skew angles on skew bridges during earthquakes[J]. Journal of Harbin Engineering University, 2012, 33(2): 155-159. (in Chinese) doi: 10.3969/j.issn.1006-7043.201010032
[2]	庄卫林, 刘振宇, 蒋劲松. 汶川大地震公路桥梁震害分析及对策[J]. 岩石力学与工程学报, 2009, 28(7): 1377-1387. doi: 10.3321/j.issn:1000-6915.2009.07.011 ZHUANG Wei-lin, LIU Zhen-yu, JIANG Jin-song. Earthquake-induced damage analysis of highway bridges inWenchuan earthquake and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1377-1387. (in Chinese) doi: 10.3321/j.issn:1000-6915.2009.07.011
[3]	MENG J Y, LUI E M, LIU Y. Dynamic response of skew highway bridges[J]. Journal of Earthquake Engineering, 2001, 5(2): 205-223.
[4]	TIRASIT P, KAWASHIMA K. Effect of nonlinear seismic torsion on the performance of skewed bridge piers[J]. Journal of Earthquake Engineering, 2008, 12(6): 980-998. doi: 10.1080/13632460701673019
[5]	YANG C S W, WERNER S D, DESROCHES R. Seismic fragility analysis of skewed bridges in the central southeastern United States[J]. Engineering Structures, 2015, 83(1): 116-128.
[6]	KUNIN J, ALAMPALLI S. Integral abutment bridges: current practice in United States and Canada[J]. Journal of Performance of Constructed Facilities, 2000, 14(3): 104-111. doi: 10.1061/(ASCE)0887-3828(2000)14:3(104)
[7]	黄福云, 单玉麟, 罗小烨, 等. 基于位移的整体桥混凝土桩基抗震设计准则[J]. 中国公路学报, 2021, 34(5): 99-109. doi: 10.3969/j.issn.1001-7372.2021.05.010 HUANG Fu-yun, SHAN Yu-lin, LUO Xiao-ye, et al. Displacement-based seismic design criteria of concrete piles in integral abutment jointless bridges[J]. China Journal of Highway and Transport, 2021, 34(5): 99-109. (in Chinese) doi: 10.3969/j.issn.1001-7372.2021.05.010
[8]	GOEL R K. Earthquake characteristics of bridges with integral abutments[J]. Journal of Structural Engineering, 1997, 123(11): 1435-1443. doi: 10.1061/(ASCE)0733-9445(1997)123:11(1435)
[9]	DUNKER K F, LIU D J. Foundations for integral abutments[J]. Practice Periodical on Structural Design and Construction, 2007, 12(1): 22-30. doi: 10.1061/(ASCE)1084-0680(2007)12:1(22)
[10]	ERHAN S, DICLELI M. Comparative assessment of the seismic performance of integral and conventional bridges with respect to the differences at the abutments[J]. Bulletin of Earthquake Engineering, 2015, 13(2): 653-677. doi: 10.1007/s10518-014-9635-8
[11]	HASSIOTIS S, ROMAN E. A survey of current issues on the use of integral abutment bridges[J]. Bridge Structures, 2005, 1(2): 81-101. doi: 10.1080/15732480500125635
[12]	XU Ming, LIU Peng-fei. Response of full-height frame integral abutments subjected to seismic motions[J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 356-368. doi: 10.1016/j.soildyn.2019.03.024
[13]	SHAMSABADI A, KAPUSKAR M. Nonlinear soil-abutment-foundation-structure interaction analysis of skewed bridges subjected to near-field ground motions[J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2202(1): 192-205. doi: 10.3141/2202-23
[14]	ZHAO Qiu-hong, DONG Shuo, WANG Qing-wei. Seismic response of skewed integral abutment bridges under near-fault ground motions, including soil-structure interaction[J]. Applied Sciences, 2021, 11(7): 3217. doi: 10.3390/app11073217
[15]	赵秋红, 张冀豪, 陈宝春. 整体式斜交桥抗震性能分析[J]. 地震工程与工程振动, 2018, 38(4): 34-40. doi: 10.13197/j.eeev.2018.04.34.zhaoqh.006 ZHAO Qiu-hong, ZHANG Ji-hao, CHEN Bao-chun. Seismic analysis on skewed integral abutment bridges. [J]. Journal of Earthquake Engineering and Engineering Dynamics, 2018, 38(4): 34-40. (in Chinese) doi: 10.13197/j.eeev.2018.04.34.zhaoqh.006
[16]	黄福云, 庄一舟, 付毳, 等. 无伸缩缝梁桥抗震性能与设计计算方法研究[J]. 地震工程与工程振动, 2015, 35(5): 15-22. doi: 10.13197/j.eeev.2015.05.15.huangfy.003 HUANG Fu-yun, ZHUANG Yi-zhou, FU Cui, et al. Review on the seismic performance and simplified design method of jointless bridge[J]. Journal of Earthquake Engineering and Engineering Dynamics, 2015, 35(5): 15-22. (in Chinese) doi: 10.13197/j.eeev.2015.05.15.huangfy.003
[17]	ITANI A M, PEKAN G. Seismic performance of steel plate girder bridges with integral abutments[R]. Reno: University of Nevada, 2011.
[18]	VASHEGHANI-FARAHANI R, ZHAO Q H, BURDETTE E G. Seismic analysis of integral abutment bridge in Tennessee, including soil-structure interaction[J]. Transportation Rese arch Record: Journal of the Transportation Research Board, 2010, 2201(1): 70-79. doi: 10.3141/2201-09
[19]	赵秋红, 齐朝阳, 安泽宇, 等. 考虑SSI的整体式钢桥抗震性能参数分析[J]. 交通运输工程学报, 2018, 18(5): 35-46. doi: 10.3969/j.issn.1671-1637.2018.05.004 ZHAO Qiu-hong, QI Zhao-yang, AN Ze-yu, et al. Parametric analysis on seismic behavior of integral abutment steel bridge considering SSI[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 35-46. (in Chinese) doi: 10.3969/j.issn.1671-1637.2018.05.004
[20]	SHERAFATI A, AZIZINAMINI A. Flexible pile head in jointless bridges: experimental investigation[J]. Journal of Bridge Engineering, 2015, 20(4): 04014071. doi: 10.1061/(ASCE)BE.1943-5592.0000628
[21]	AZIZINAMINI A, YAKEL A, SHERAFATI A, et al. Flexible Pile head in jointless bridges: design provisions for H-piles in cohesive soils[J]. Journal of Bridge Engineering, 2016, 21(3): 04015064. doi: 10.1061/(ASCE)BE.1943-5592.0000791
[22]	齐朝阳. 整体式桥台-桩节点抗震性能试验研究[D]. 天津: 天津大学, 2017. QI Zhao-yang. Experimental research on seismic behavior of integral abutment-pile joint[D]. Tianjin: Tianjin University, 2017. (in Chinese)
[23]	KOZAK D L, LAFAVE J M, FAHNESTOCK L A. Seismic modeling of integral abutment bridges in Illinois[J]. Engineering Structures, 2018, 165: 170-183. doi: 10.1016/j.engstruct.2018.02.088
[24]	汤虎, 李建中. 板式橡胶支座桥梁地震位移控制方法[J]. 中国公路学报, 2013, 26(3): 110-116. doi: 10.3969/j.issn.1001-7372.2013.03.012 TANG Hu, LI Jian-zhong. Displacement control method for continuous bridges on laminated rubber bearings under earthquake excitation[J]. China Journal of Highway and Transport, 2013, 26(3): 110-116. (in Chinese) doi: 10.3969/j.issn.1001-7372.2013.03.012
[25]	QUINN B H, CIVJAN S A. Parametric study on effects of pile orientation in integral abutment bridges[J]. Journal of Bridge Engineering, 2017, 22(4): 04016132. doi: 10.1061/(ASCE)BE.1943-5592.0000952
[26]	ZORDAN T, BRISEGHELLA B, LAN C. Parametric and pushover analyses on integral abutment bridge[J]. Engineering Structures, 2011, 33(2): 502-515. doi: 10.1016/j.engstruct.2010.11.009
[27]	SHAMSABADI A, ROLLINS K M, KAPUSKAR M. Nonlinear soil-abutment-bridge structure interaction for seismic performance-based design[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(6): 707-720. doi: 10.1061/(ASCE)1090-0241(2007)133:6(707)
[28]	DICLELI M. Integral abutment-backfill behavior on sand soil—pushover analysis approach[J]. Journal of Bridge Engineering, 2005, 10(3): 354-364. doi: 10.1061/(ASCE)1084-0702(2005)10:3(354)
[29]	孔令刚, 姜丽红, 陈仁朋, 等. 考虑桩头约束的水平受荷单桩响应分析[J]. 应用力学学报, 2014, 31(3): 393-399, 490-491. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201403017.htm KONG Ling-gang, JIANG Li-hong, CHEN Ren-peng, et al. Response of single pile with partial pile head fixity subjected to lateral loading[J]. Chinese Journal of Applied Mechanics, 2014, 31(3): 393-399, 490-491. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201403017.htm
[30]	李枝军, 葛飞, 徐秀丽, 等. 板式橡胶支座性能有限元模拟与试验研究[J]. 东南大学学报(自然科学版), 2013, 43(6): 1299-1304. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201306031.htm LI Zhi-jun, GE Fei, XU Xiu-li, et al. Finite element simulation and experimental study of property for elastomeric pad bearing[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(6): 1299-1304. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201306031.htm