整体桥H型钢-RC阶梯桩与土相互作用拟静力试验

庄一舟; 宋琨生; 宋永青; 陈国栋; 黄福云; 陈良

doi:10.19818/j.cnki.1671-1637.2022.05.008

整体桥H型钢-RC阶梯桩与土相互作用拟静力试验

doi: 10.19818/j.cnki.1671-1637.2022.05.008

1.
浙江工业大学土木工程学院，浙江杭州 310014
2.
福州大学土木工程学院，福建福州 350108

基金项目:

国家自然科学基金项目 51778147

详细信息

作者简介:
庄一舟(1964-)，男，浙江奉化人，浙江工业大学教授，工学博士，从事桥梁工程研究

中图分类号: U441
计量
- 文章访问数: 529
- HTML全文浏览量: 176
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-17
- 刊出日期: 2022-10-25

Quasi-static test on H-shaped steel-RC stepped pile-soil interaction of integral bridge

1.
College of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China
2.
College of Civil Engineering, Fuzhou University, Fuzhou 350108, Fujian, China

Funds:

National Natural Science Foundation of China 51778147

More Information

Author Bio:
ZHUANG Yi-zhou(1964-), male, professor, PhD, yizhouzhuang@qq.com

摘要

摘要: 以H型钢-RC阶梯桩模型试验为背景，进行了2根H型钢-RC阶梯桩(HS-RC-0.25、HS-RC-0.50)及1根H型钢桩(HS)的低周往复荷载拟静力试验；在桩顶施加水平位移荷载，埋设应变片与土压力计，采用特殊设计的桩身水平变位测试方法，得到了H型钢-RC阶梯桩桩身破坏特点、沿桩深方向的桩身水平位移与应变、骨架曲线和滞回性能曲线；利用OpenSEES对比分析了桩顶自由与固定条件下阶梯桩桩顶水平变位能力，得到了阶梯桩水平承载力折减系数与转化系数，对比了利用折减系数得到的模型桩水平承载力计算值与试验值。试验结果表明：H型钢桩的桩顶弹性变形为2~25 mm，其水平变形能力强，承载能力好，加载全过程滞回环饱满，耗能效果好；刚度比对阶梯桩的破坏模式无显著影响，阶梯桩的上段钢桩均无明显的屈曲破坏，变截面处混凝土严重剥落且破坏位置相同；随刚度比增大，阶梯桩-土体系屈服位移及屈服荷载均提高，HS-RC-0.25较HS-RC-0.50桩顶屈服位移减小了29.15%，桩身应变突变减小；阶梯桩的滞回环在加载初期因为滑移表现为捏拢状，而在加载后期过渡为饱满的梭形，耗能效果良好，HS-RC-0.50加载全过程的耗能比HS-RC-0.25多25.4%，具有较好的水平变形能力；对比试验值，HS-RC-0.25的计算误差为-9.68%，HS-RC-0.50的计算误差为-2.47%。可见，HS-RC阶梯桩能满足整体桥桩基的水平变形需求，利用折减系数能较好地计算阶梯桩的水平承载力特征值。
- 桥梁工程 /
- 整体桥 /
- H型钢桩 /
- H型钢-RC阶梯桩 /
- 桩与土相互作用 /
- 拟静力试验 /
- 有限元分析
Abstract: On the basis of H-shaped steel-RC stepped pile model tests, the quasi-static tests of 2 H-shaped steel-RC stepped piles (HS-RC-0.25, HS-RC-0.50) and an H-shaped steel (HS) pile under the low cyclic repeated loading were carried out. A horizontal displacement load was applied on the pile top, and the strain and soil pressure gauges were embedded, a specially designed test method for the horizontal displacement of the pile body was adopted, and the failure characteristics of the HS-RC stepped pile, the horizontal displacement and strain of the pile body along the pile depth, skeleton curve, and hysteretic behavior curve were obtained. The horizontal displacement abilities of the stepped pile top under free and fixed conditions were compared and analyzed by OpenSEES. The reduction coefficient and conversion coefficient of the horizontal bearing capacity of the stepped pile were obtained, and the calculated value obtained by the reduction coefficient and test value of horizontal bearing capacity of the model pile were compared. Test results show that the elastic deformation range of the pile top of the HS pile is 2-25 mm, and the pile has strong horizontal deformation ability, positive bearing capacity, full hysteresis loop during the whole loading process, and excellent energy consumption effect. The stiffness ratio has no significant effect on the failure mode of the stepped pile. The upper steel pile of the stepped pile has no apparent buckling failure, and the concrete at the variable section is seriously peeled off with the same failure position. With the increase in the stiffness ratio, the yield displacement and yield load of the stepped pile-soil system increase. Compared with that of HS-RC-0.50, the yield displacement of HS-RC-0.25 decreases by 29.15%, and the strain mutation of the pile body decreases. The hysteresis loop of the stepped pile is pinched at the initial loading stage due to slip and becomes spindle-shaped at the later loading stage. The energy consumption effect is positive, and the energy consumption of HS-RC-0.50 during the whole loading process is 25.4% more than that of HS-RC-0.25, which shows an excellent horizontal deformation ability. Compared with the experimental value, the calculation error of HS-RC-0.25 is -9.68%, while the calculation error of HS-RC-0.50 is -2.47%. The HS-RC stepped pile can meet the horizontal deformation requirements of the integral abutment bridge pile foundation, and the reduction coefficient can be used to better calculate the stepped pile's horizontal bearing capacity characteristic value.
- bridge engineering /
- integral bridge /
- H-shaped steel pile /
- H-shaped steel-RC stepped pile /
- pile-soil interaction /
- quasi-static test /
- finite element analysis

HTML全文

图 1 试件横截面(单位：mm)

Figure 1. Cross sections of specimens (unit: mm)

下载: 全尺寸图片幻灯片

图 2 RC截面配筋(单位：mm)

Figure 2. RC sectional reinforcements (unit: mm)

下载: 全尺寸图片幻灯片

图 3 HS-RC桩制作

Figure 3. HS-RC pile fabrication

下载: 全尺寸图片幻灯片

图 4 试验土箱

Figure 4. Testing soil box

下载: 全尺寸图片幻灯片

图 5 砂土材性试验

Figure 5. Sand material tests

下载: 全尺寸图片幻灯片

图 6 水平位移加载历程

Figure 6. Horizontal displacement loading history

下载: 全尺寸图片幻灯片

图 7 传感器布置(单位：mm)

Figure 7. Arrangements of sensors (unit: mm)

下载: 全尺寸图片幻灯片

图 8 模型桩破坏模式

Figure 8. Failure modes of model piles

下载: 全尺寸图片幻灯片

图 9 桩身位移曲线

Figure 9. Displacement curves of pile bodies

下载: 全尺寸图片幻灯片

图 10 桩身应变分布曲线

Figure 10. Strain distribution curves of pile bodies

下载: 全尺寸图片幻灯片

图 11 桩身应变时间历程

Figure 11. Strain time histories of pile bodies

下载: 全尺寸图片幻灯片

图 12 桩身应变比较

Figure 12. Strain comparison of pile bodies

下载: 全尺寸图片幻灯片

图 13 桩身弯矩

Figure 13. Bending moments of pile bodies

下载: 全尺寸图片幻灯片

图 14 桩侧土压力

Figure 14. Earth pressures of pile sides

下载: 全尺寸图片幻灯片

图 15 土压力-桩身位移曲线

Figure 15. Soil pressure-pile body displacement curves

下载: 全尺寸图片幻灯片

图 16 滞回曲线

Figure 16. Hysteresis curves

下载: 全尺寸图片幻灯片

图 17 模型桩骨架曲线

Figure 17. Skeleton curves of model piles

下载: 全尺寸图片幻灯片

图 18 模型桩耗能特性

Figure 18. Energy consumption characteristics of model piles

下载: 全尺寸图片幻灯片

图 19 模型桩刚度退化曲线

Figure 19. Stiffness degradation curves of model piles

下载: 全尺寸图片幻灯片

图 20 桩与土相互作用模型及纤维截面网格划分

Figure 20. Pile-soil interaction model and fiber section meshing

下载: 全尺寸图片幻灯片

图 21 有限元模型验证

Figure 21. Validation of finite element model

下载: 全尺寸图片幻灯片

图 22 有限元与试验桩身位移对比

Figure 22. Comparison of finite element and test pile body displacements

下载: 全尺寸图片幻灯片

图 23 桩顶承载力

Figure 23. Bearing capacities of pile top

下载: 全尺寸图片幻灯片

图 24 承载力归一化处理

Figure 24. Normalization of bearing capacity

下载: 全尺寸图片幻灯片

表 1 试件参数

Table 1. Parameters of specimens

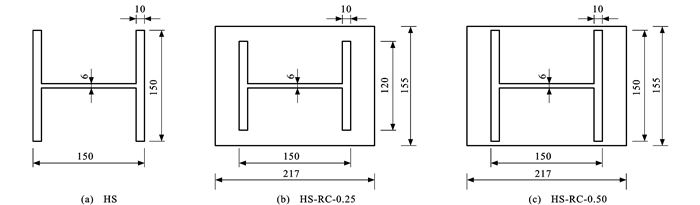
编号	材料种类	桩长/m	抗弯刚度/(kN·m²)
HS	Q235	3.5	1 125.49
HS-RC-0.25	Q235/C40	1.4/2.1	576.49/2 052.30
HS-RC-0.50	Q235/C40	1.4/2.1	1 125.49/2 052.30

下载: 导出CSV

表 2 砂土参数

Table 2. Parameters of sand

参数	含水量/%	密度/(g·cm^-3)	内摩擦角/(°)	平均标贯击数	相对密实度/%
取值	4.6	1.90	35	16	53

下载: 导出CSV

表 3 HS-RC阶梯桩尺寸

Table 3. Dimensions of HS-RC stepped piles

刚度比	HS段				RC段
刚度比	腹板高/mm	腹板厚/mm	翼缘厚/mm	翼缘宽/mm	长/mm	宽/mm	配筋率/%
0.1	544	14	28	288	700	500	1.6
0.2				362
0.3				415
0.4				456
0.5				490

下载: 导出CSV

表 4 阶梯桩水平承载力折减系数(桩顶自由)

Table 4. Reduction factors of horizontal bearing capacity of stepped pile (top freedom)

长度比	不同刚度比的折减系数
长度比	0.1	0.2	0.3	0.4	0.5
0.20	0.522	0.675	0.755	0.803	0.834
0.33	0.407	0.553	0.653	0.724	0.777
0.50	0.391	0.522	0.623	0.703	0.760
1.00	0.390	0.519	0.615	0.694	0.760

下载: 导出CSV

表 5 阶梯桩水平承载力转化系数(桩顶固定)

Table 5. Transformation factors of horizontal bearing capacity of stepped piles (top fixed)

长度比	不同刚度比的转化系数
长度比	0.1	0.2	0.3	0.4	0.5
0.20	2.552	2.450	2.463	2.514	2.541
0.33	2.726	2.688	2.664	2.661	2.672
0.50	2.639	2.656	2.644	2.632	2.656
1.00	2.638	2.636	2.636	2.635	2.633
均值	2.639	2.607	2.602	2.611	2.625

下载: 导出CSV

表 6 试件参数

Table 6. Parameters of specimens

编号	混凝土材料种类	截面形式及尺寸/mm	桩长/m
UC-1^[30]	U130/C40	矩形, 140×100矩形, 217×155	1.4/2.1
UC-2^[30]	U130/C40	圆形，直径为100/155	1.4/2.1
UC-3^[30]	U130/C40	H形, 140×120×40×40矩形, 217×155	1.4/2.1
RC-1^[29]	C40	矩形, 217×155	3.5
RC-2^[29]	C40	圆形，直径为155	3.5

下载: 导出CSV

表 7 阶梯桩承载力特征值比较

Table 7. Characteristic value comparison of bearing capacities of stepped piles

试件编号	长度比	刚度比	试验值/kN	计算值/kN	误差/%
HS-RC-0.25	0.48	0.25	4.661	4.210	-9.68
HS-RC-0.50		0.50	5.592	5.454	-2.47
UC-1^[30]		0.22	4.488	3.895	-13.21
UC-2^[30]		0.22	2.377	2.108	-12.76
UC-3^[30]		0.28	4.650	4.170	-10.32

下载: 导出CSV

参考文献(30)

[1]	黄福云, 单玉麟, 罗小烨, 等. 基于位移的整体桥混凝土桩基抗震设计准则[J]. 中国公路学报, 2021, 34(5): 99-109. doi: 10.3969/j.issn.1001-7372.2021.05.010 HUANG Fu-yun, SHAN Yu-lin, LUO Xiao-ye, et al. Displacement-based seismic design criteria of concrete piles in integral abutment jointless bridges[J]. China Journal of Highway and Transport, 2021, 34(5): 99-109. (in Chinese) doi: 10.3969/j.issn.1001-7372.2021.05.010
[2]	WHITE H, PÉTURSSON H, COLLIN P. Integral abutment bridges: the European way[J]. Practice Periodical on Structural Design and Construction, 2010, 15(3): 201-208. doi: 10.1061/(ASCE)SC.1943-5576.0000053
[3]	KUNIN J, ALAMPALLI S. Integral abutment bridges: current practice in United States and Canada[J]. Journal of Performance of Constructed Facilities, 2000, 14(3): 104-111. doi: 10.1061/(ASCE)0887-3828(2000)14:3(104)
[4]	AL-ANI M, MURASHEV A, PALERMO A, et al. Criteria and guidance for the design of integral bridges[J]. Proceedings of the Institution of Civil Engineers Bridge Engineering, 2018, 171(3): 143-154. doi: 10.1680/jbren.17.00014
[5]	LAFAVE J M, BRAMBILA G, KODE U, et al. Field behavior of integral abutment bridges under thermal loading[J]. Journal of Bridge Engineering, 2021, 26(4): 04021013. doi: 10.1061/(ASCE)BE.1943-5592.0001677
[6]	DUNKER K F, LIU D. Foundations for integral abutments[J]. Practice Periodical on Structural Design and Construction, 2007, 12(1): 22-30. doi: 10.1061/(ASCE)1084-0680(2007)12:1(22)
[7]	罗小烨, 陈宝春, 黄福云, 等. 不同类型桩基支撑的整体桥力学性能[J]. 建筑科学与工程学报, 2020, 37(5): 151-160. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG202005016.htm LUO Xiao-ye, CHEN Bao-chun, HUANG Fu-yun, et al. Mechanical property of integral bridge supported by different types of pile foundations[J]. Journal of Architecture and Civil Engineering, 2020, 37(5): 151-160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG202005016.htm
[8]	KONG B, CAI C S, ZHANG Y. Parametric study of an integral abutment bridge supported by prestressed precast concrete piles[J]. Engineering Structures, 2016(120): 37-48.
[9]	BAKROON M, DARYAEI R, AUBRAM D, et al. Numerical evaluation of buckling in steel pipe piles during vibratory installation[J]. Soil Dynamics and Earthquake Engineering, 2019, 122: 327-336. doi: 10.1016/j.soildyn.2018.08.003
[10]	FAR N E, MALEKI S, BARGHIAN M. Design of integral abutment bridges for combined thermal and seismic loads[J]. Earthquakes and Structures, 2015, 9(2): 415-430. doi: 10.12989/eas.2015.9.2.415
[11]	DICLELI M. Analytical prediction of thermal displacement capacity of integral bridges built on sand[J]. Advances in Structural Engineering, 2005, 8(1): 15-30. doi: 10.1260/1369433053749661
[12]	KAMEL M R, BENAK J V, TADROS M K, et al. Prestressed concrete piles in jointless bridges[J]. PCI Journal, 1996, 41(2): 56-67. doi: 10.15554/pcij.03011996.56.67
[13]	于天来, 李伯岩, 刘洋, 等. 整体式桥台桥梁细部构造设计[J]. 中外公路, 2011, 31(2): 193-195. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201102049.htm YU Tian-lai, LI Bo-yan, LIU Yang, et al. Detailed structural design of integral abutment bridge[J]. Journal of China and Foreign Highway, 2011, 31(2): 193-195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201102049.htm
[14]	RAZMI J, AGGOUR M S, LADANI L. Performance of piles in integral abutment bridges under thermo-mechanical cyclic loads[J]. Bridge Structures, 2014, 10(1): 11-17. doi: 10.3233/BRS-140066
[15]	VERMA M, MISHRA S S. Temperature-driven fatigue life of reinforced concrete integral bridge pile considering nonlinear soil-structure interaction[J]. Structural Concrete, 2020, 21(6): 2565-2583. doi: 10.1002/suco.202000049
[16]	YIN Shi-ping, JING Lei, LYU Heng-lin. Experimental analysis of bond between corroded steel bar and concrete confined with textile-reinforced concrete[J]. Journal of Materials in Civil Engineering, 2019, 31(10): 04019208. doi: 10.1061/(ASCE)MT.1943-5533.0002856
[17]	洪锦祥, 彭大文. 桩基础的整体式桥台桥梁受力性能研究[J]. 中国公路学报, 2002, 15(4): 43-48. doi: 10.3321/j.issn:1001-7372.2002.04.013 HONG Jin-xiang, PENG Da-wen. Research on the loaded property of integral abutment bridges with flexible piles[J]. China Journal of Highway and Transport, 2002, 15(4): 43-48. (in Chinese) doi: 10.3321/j.issn:1001-7372.2002.04.013
[18]	ISMAEL N F. Behavior of step tapered bored piles in sand under static lateral loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(5): 669-676. doi: 10.1061/(ASCE)GT.1943-5606.0000265
[19]	吴泽军, 耿大新, 方焘. 变截面桩的水平荷载模型试验研究[J]. 铁道建筑, 2011, 51(8): 103-105. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201108034.htm WU Ze-jun, GENG Da-xin, FANG Tao. Model test on horizontal load of variable cross-section pile[J]. Railway Engineering, 2011, 51(8): 103-105. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201108034.htm
[20]	刘新荣, 方焘, 耿大新, 等. 大直径变径桩横向承载特性模型试验[J]. 中国公路学报, 2013, 26(6): 80-86, 190. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201306013.htm LIU Xin-rong, FANG Tao, GENG Da-xin, et al. Model test on lateral bearing behaviors of large diameter pile with variable cross section[J]. China Journal of Highway and Transport, 2013, 26(6): 80-86, 190. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201306013.htm
[21]	邹贵华, 胡伟, 刘顺凯, 等. 变截面桩水平承载规律研究[J]. 科学技术与工程, 2016, 16(33): 108-112. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201633019.htm ZOU Gui-hua, HU Wei, LIU Shun-kai, et al. Research on horizontal bearing characters of variable cross-sectional pile[J]. Science and Technology and Engineering, 2016, 16(33): 108-112. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201633019.htm
[22]	李宝建, 李光范, 胡伟, 等. 材料复合桩的现场承载性能试验研究[J]. 岩土力学, 2015, 36(增2): 629-632. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2091.htm LI Bao-jian, LI Guang-fan, HU Wei, et al. Experimental study of field bearing capacity of material composite piles[J]. Rock and Soil Mechanics, 2015, 36(S2): 629-632. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2091.htm
[23]	陈宝春, 陈国栋, 苏家战, 等. 采用UHPC-RC阶梯桩的整体桥试设计[J]. 建筑科学与工程学报, 2018, 35(1): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG201801002.htm CHEN Bao-chun, CHEN Guo-dong, SU Jia-zhan, et al. Trial-design study on integral abutment bridge by using UHPC-RC stagewise piles[J]. Journal of Architecture and Civil Engineering, 2018, 35(1): 1-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG201801002.htm
[24]	黄福云, 庄一舟, 付毳, 等. 无伸缩缝梁桥抗震性能与设计计算方法研究[J]. 地震工程与工程振动, 2015, 35(5): 15-22. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201505003.htm HUANG Fu-yun, ZHUANG Yi-zhou, FU Cui, et al. Review on the seismic performance and simplified design method of jointless bridge[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(5): 15-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201505003.htm
[25]	赵秋红, 齐朝阳, 安泽宇, 等. 考虑SSI的整体式钢桥抗震性能参数分析[J]. 交通运输工程学报, 2018, 18(5): 35-46. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201805005.htm ZHAO Qiu-hong, QI Zhao-yang, AN Ze-yu, et al. Parametric analysis on seismic behavior of integral abutment steel bridge considering SSI[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 35-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC201805005.htm
[26]	HUANG Fu-yun, WU Sui-wen, LUO Xiao-ye, et al. Pseudo-static low cycle test on the mechanical behavior of PHC pipe piles with consideration of soil-pile interaction[J]. Engineering Structures, 2018, 171: 992-1006.
[27]	赵金钢, 杜斌, 占玉林. OpenSees中Mander模型用于模拟钢筋混凝土柱滞回性能的适用性[J]. 兰州理工大学学报, 2017, 43(5): 127-133. https://www.cnki.com.cn/Article/CJFDTOTAL-GSGY201705022.htm ZHAO Jin-gang, DU Bin, ZHAN Yu-lin. Applicability of Mander model in OpenSees for simulation of hysteretic behavior of reinforced concrete column[J]. Journal of Lanzhou University of Technology, 2017, 43(5): 127-133. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GSGY201705022.htm
[28]	刘亚明, 司炳君, 何福. 单桩-土相互作用非线性数值分析模型[J]. 防灾科技学院学报, 2018, 20(2): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-FZJS201802001.htm LIU Ya-ming, SI Bing-jun, HE Fu. Nonlinear numerical analysis model for single pile-soil interaction[J]. Journal of Institute of Disaster Prevention, 2018, 20(2): 1-5. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FZJS201802001.htm
[29]	李增锋. 基于位移的混凝土桩-土相互作用拟静力试验研究[D]. 福州: 福州大学, 2018. LI Zeng-feng. Quasi static test research of concrete pile-soil interaction based on displacement[D]. Fuzhou: Fuzhou University, 2018. (in Chinese)
[30]	刘名琦. 整体桥UHPC-RC阶梯桩-土相互作用试验研究[D]. 福州: 福州大学, 2020. LIU Ming-qi. Experimental study on UHPC-RC segmental pile-soil interaction of integral abutment bridge[D]. Fuzhou: Fuzhou University, 2020. (in Chinese)