下承式拱桥合理拱轴线的解析解与计算方法

张国靖; 刘永健; 刘江

doi:10.19818/j.cnki.1671-1637.2022.05.013

下承式拱桥合理拱轴线的解析解与计算方法

doi: 10.19818/j.cnki.1671-1637.2022.05.013

张国靖^1,,
刘永健^{1, 2, ,},
刘江^{1, 2}

1.
长安大学公路学院, 陕西西安 710064
2.
长安大学公路大型结构安全教育部工程研究中心, 陕西西安 710064

基金项目:

国家重点研发计划 2016YFC0701202

国家自然科学基金项目 51178051

中央高校基本科研业务费专项资金项目 300102219310

详细信息

作者简介:
张国靖(1992-)，男，陕西榆林人，长安大学工学博士研究生，从事大跨桥梁结构研究

通讯作者:
刘永健(1966-)，男，江西玉山人，长安大学教授，工学博士

中图分类号: U442.5
计量
- 文章访问数: 529
- HTML全文浏览量: 272
- PDF下载量: 88
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-26
- 刊出日期: 2022-10-25

Analytical solution and calculation method of reasonable arch axis of through arch bridge

ZHANG Guo-jing^1
,,
LIU Yong-jian^{1, 2
, ,},
LIU Jiang^{1, 2}

1.
School of Highway, Chang'an University, Xi'an 710064, Shaanxi, China
2.
Research Center of Highway Large Structure Engineering on Safety of Ministry of Education, Chang'an University, Xi'an 710064, Shaanxi, China

Funds:

National Key Research and Development Program of China 2016YFC0701202

National Natural Science Foundation of China 51178051

Fundamental Research Funds for the Central Universities 300102219310

More Information

Author Bio:
ZHANG Guo-jing (1992-), male, doctoral student, izhangguojing@126.com

LIU Yong-jian(1966-), male, professor, PhD, liuyongjian@chd.edu.cn

摘要

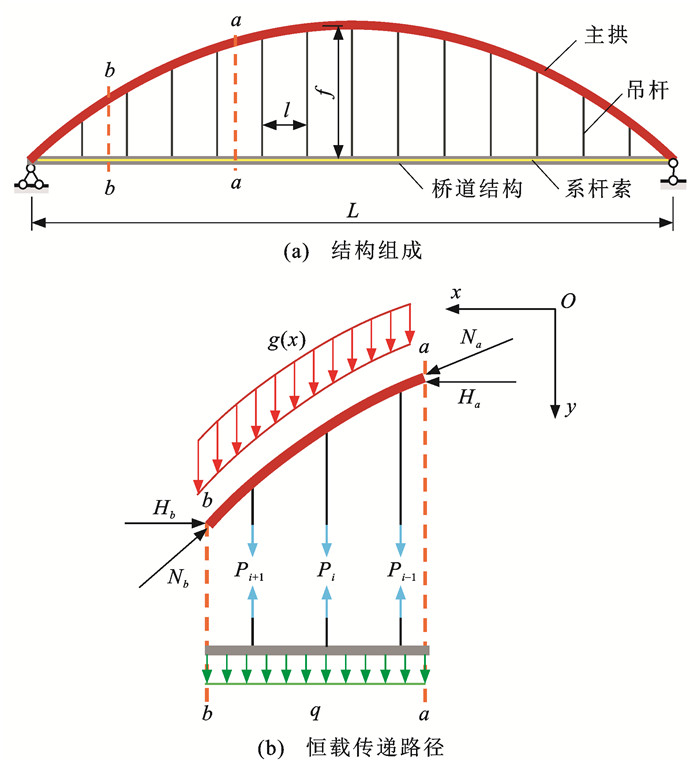
摘要: 为了得到下承式拱桥合理拱轴线的解析解与计算方法，建立了恒载作用模式和合理拱轴线微分方程，得到合理拱轴线的解析解；在解析解的基础上，定义了主拱恒载占比系数，得到了基于矢跨比和主拱恒载占比系数的合理拱轴线快速求解计算方法；采用拱桥设计规范、工程案例与相关研究成果，验证了本文方法的可靠性。研究结果表明：下承式拱桥的恒载作用模式可等效为连续均布恒载+主拱恒载的形式，合理拱轴线为悬链线，相应的拱轴系数由矢跨比和主拱恒载占比系数共同决定；拟合出的不同矢跨比下的拱轴系数与主拱恒载占比系数的函数关系式为线性相关关系，决定系数大于0.99，说明拟合公式准确；工程中下承式拱桥矢跨比范围为1/3~1/8，相应的拱轴系数范围为1.000~1.792，常见的矢跨比范围为1/4~1/5，相应的拱轴系数范围为1.000~1.465，与工程案例中拱轴系数统计结果的吻合度较高，说明计算结果可靠；工程中常见主拱恒载占比系数范围为0.1~0.5，对应的拱轴系数范围为1.102~1.364，与拱桥设计规范中的取值范围接近，证明了规范取值的合理性；当主拱恒载占比系数小于0.5且矢跨比小于1/7，或主拱恒载占比系数小于0.1时，拱轴系数接近于1.000，即合理拱轴线可采用二次抛物线；利用查表法或简化公式法，可以快速求得合理拱轴线方程；与已有研究成果相比较，主拱截面弯矩、偏心距和偏心距平方和的偏差均在5%以内，证明了本文计算方法的正确性。
- 桥梁工程 /
- 下承式拱桥 /
- 合理拱轴线 /
- 解析方程法 /
- 拱轴系数 /
- 主拱恒载占比
Abstract: To obtain the analytical solution and calculation method of the reasonable arch axis of through arch bridge, the dead load action mode and differential equation of the reasonable arch axis were established, and the analytical solution of the reasonable arch axis was determined. Based on the analytical solution, the dead load ratio of main arch was defined. Based on the rise-span ratio and dead load ratio of main arch, a quick calculation method of the reasonable arch axis was obtained. The reliability of the proposed method was confirmed by arch bridge design specifications, engineering cases, and related research achievements. Research results show that the dead load action mode of through arch bridge can be equivalent to the combination of continuous uniform dead load and arch dead load, the reasonable arch axis is catenary, and the corresponding arch axis coefficient is determined by the rise-span ratio and dead load ratio of main arch. The fitted functional relationships between the arch axis coefficients and dead load ratios of main arch under different rise-span ratios are a linear correlation, and the determination coefficients are greater than 0.99, indicating that the fitted equations are accurate. The rise-span ratio of through arch bridge is between 1/3 and 1/8 in engineerings, and the range of the corresponding arch axis coefficient is between 1.000 and 1.792. The common rise-span ratio ranges from 1/4 to 1/5, and the corresponding arch axis coefficient ranges from 1.000 to 1.465. The calculation results are in good agreement with the statistical results of arch axis coefficients of engineering cases, indicating that the calculation results are reliable. The common dead load ratio of main arch ranges from 0.1 to 0.5, and the corresponding arch axis coefficient ranges from 1.102 to 1.364. The calculation results are close to the value ranges in the arch bridge design specification, which proves the rationality of value range in the arch bridge design specification. When the dead load ratio of main arch is less than 0.5 and the rise-span ratio is less than 1/7, or the dead load ratio of main arch is less than 0.1, the arch axis coefficient is close to 1.000. As a result, the quadratic parabola can be used as reasonable arch axis. The reasonable arch axis equation can be obtained quickly by the look-up table method and simplified formula method. Compared with the mature research achievements, the deviations of bending moments, eccentricities and sums of squared eccentricities of main arch cross-section are within 5%, which proves the correctness of the solution method.
- bridge engineering /
- through arch bridge /
- reasonable arch axis /
- analytical equation method /
- arch axis coefficient /
- dead load ratio of main arch

HTML全文

图 1 下承式拱桥结构组成与恒载传递路径

Figure 1. Structure composition and dead load transfer path of through arch bridge

下载: 全尺寸图片幻灯片

图 2 下承式拱桥恒载分布

Figure 2. Dead load distribution of through arch bridge

下载: 全尺寸图片幻灯片

图 3 集中力连续化

Figure 3. Continuous change of concentrated loads

下载: 全尺寸图片幻灯片

图 4 下承式拱桥恒载作用模式与计算参数

Figure 4. Dead load mode and calculation parameters of through arch bridge

下载: 全尺寸图片幻灯片

图 5 合理拱轴线计算参数与平衡隔离体

Figure 5. Calculation parameters and balanced isolator of reasonable arch axis

下载: 全尺寸图片幻灯片

图 6 合理拱轴线迭代计算流程

Figure 6. Iterative calculation process of reasonable arch axis

下载: 全尺寸图片幻灯片

图 7 m随λ和f/L的变化规律

Figure 7. Variation laws of m with λ and f/L

下载: 全尺寸图片幻灯片

图 8 矢跨比统计结果

Figure 8. Statistical results of rise-span ratios

下载: 全尺寸图片幻灯片

图 9 下承式拱桥拱轴系数统计结果

Figure 9. Arch axis coefficients statistical results of through arch bridges

下载: 全尺寸图片幻灯片

图 10 拱轴系数对比

Figure 10. Comparison of arch axis coefficients

下载: 全尺寸图片幻灯片

图 11 合理拱轴线快速求解流程

Figure 11. Flow chart of quick solution of reasonable arch axis

下载: 全尺寸图片幻灯片

图 12 拱桥概况

Figure 12. Overview of arch bridge

下载: 全尺寸图片幻灯片

图 13 恒载分布模式与计算参数

Figure 13. Dead load distribution modes and calculation parameters

下载: 全尺寸图片幻灯片

图 14 合理拱轴线求解结果比较

Figure 14. Comparison of solution results of reasonable arch axis

下载: 全尺寸图片幻灯片

图 15 三铰拱弯矩和偏心距比较

Figure 15. Comparison of bending moments and eccentricities of three-hinged arch

下载: 全尺寸图片幻灯片

图 16 无铰拱弯矩和偏心距比较

Figure 16. Comparison of bending moments and eccentricities of hingless arch

下载: 全尺寸图片幻灯片

图 17 拱轴线偏心距平方和比较

Figure 17. Comparison of square sums of eccentricities of arch axis

下载: 全尺寸图片幻灯片

表 1 十座拱桥λ的统计结果

Table 1. λ statistical results of 10 arch bridges

序号	结构型式	跨径/m	桥宽/m	矢跨比	截面型式	桥道结构	桥道梁跨径/m	主拱恒载占比系数
1	钢管混凝土拱桥	46.0	18.0	1/3	单圆管型	钢筋混凝土结构	4.0	0.119
2	钢管混凝土拱桥	75.0	18.0	1/5	哑铃型	钢筋混凝土结构	4.7	0.176
3	钢管混凝土拱桥	95.5	22.4	2/9	哑铃型	钢筋混凝土结构	7.1	0.316
4	钢管混凝土拱桥	100.0	5.5	1/5	哑铃型	钢筋混凝土结构	4.1	0.251
5	钢箱拱桥	118.0	39.4	1/4	箱型	钢-混组合结构	6.0	0.110
6	钢管混凝土拱桥	136.0	11.5	1/5	桁架型	钢筋混凝土结构	8.1	0.352
7	钢管混凝土拱桥	150.0	23.5	2/9	桁架型	钢筋混凝土结构	8.0	0.431
8	钢筋混凝土拱桥	280.0	26.0	1/5	箱型	钢筋混凝土结构	12.0	0.485
9	钢管混凝土拱桥	300.0	24.0	2/11	桁架型	钢筋混凝土结构	10.0	0.337
10	钢桁拱桥	390.0	12.0	2/9	桁架型	钢-混组合结构	12.0	0.459

下载: 导出CSV

表 2 拱轴系数计算结果

Table 2. Calculation results of arch axis coefficients

主拱恒载占比系数	矢跨比
主拱恒载占比系数	1/3	1/4	1/5	1/6	1/7	1/8
0.0	1.000	1.000	1.000	1.000	1.000	1.000
0.1	1.068	1.042	1.028	1.020	1.015	1.012
0.2	1.138	1.085	1.057	1.041	1.031	1.024
0.3	1.211	1.129	1.086	1.062	1.046	1.036
0.4	1.286	1.174	1.116	1.083	1.062	1.048
0.5	1.364	1.220	1.146	1.104	1.078	1.060
0.6	1.444	1.267	1.177	1.126	1.094	1.072
0.7	1.527	1.315	1.208	1.148	1.110	1.085
0.8	1.612	1.364	1.240	1.170	1.126	1.097
0.9	1.701	1.414	1.272	1.192	1.143	1.110
1.0	1.792	1.465	1.305	1.215	1.159	1.123

下载: 导出CSV

表 3 十座拱桥拱轴系数计算结果

Table 3. Calculation results of arch axis coefficients of 10 arch bridges

序号	跨径/m	矢跨比	主拱恒载占比系数	本文计算拱轴系数	原设计拱轴系数	拱轴系数偏差
1	46	1/3	0.119	1.075	1.000	-0.075
2	75	1/5	0.176	1.050	1.000	-0.050
3	96	2/9	0.316	1.116	1.347	0.231
4	100	1/5	0.251	1.073	1.167	0.094
5	118	1/4	0.110	1.044	1.100	0.056
6	136	1/5	0.352	1.103	1.167	0.064
7	150	2/9	0.431	1.160	1.167	0.007
8	280	1/5	0.485	1.144	1.167	0.023
9	300	2/11	0.337	1.085	1.100	0.015
10	390	2/9	0.459	1.171	1.200	0.029

下载: 导出CSV

表 4 不同f/L下λ与m的关系式拟合结果

Table 4. Fitting results of relationships between λ and m under different rise-span ratios

矢跨比	拟合公式	决定系数	公式编号
1/3	m=0.791 3λ+0.981 0	0.997 9	(22)
1/4	m=0.465 0λ+0.992 5	0.999 1	(23)
1/5	m=0.305 0λ+0.996 1	0.999 5	(24)
1/6	m=0.215 0λ+0.998 0	0.999 7	(25)
1/7	m=0.159 3λ+0.998 9	0.999 9	(26)
1/8	m=0.122 5λ+0.998 9	0.999 9	(27)

下载: 导出CSV

表 5 拱轴线坐标

Table 5. Arch axis coordinates

水平向坐标/m	竖向坐标/m	水平向坐标/m	竖向坐标/m
0.000	0.000	39.000	8.010
3.000	0.048	42.000	9.297
6.000	0.190	45.000	10.681
9.000	0.426	48.000	12.164
12.000	0.757	51.000	13.744
15.000	1.179	54.000	15.422
18.000	1.671	57.000	17.202
21.000	2.316	60.000	19.081
24.000	3.026	63.000	21.061
27.000	3.831	66.000	23.143
30.000	4.731	69.000	25.327
33.000	5.727	72.000	27.614
36.000	6.820	75.000	30.000

下载: 导出CSV

表 6 最大弯矩和最大偏心距计算结果

Table 6. Calculation results of maximum bending moments and maximum eccentricities

方法	三铰拱		无铰拱
方法	最大弯矩/(kN·m)	最大偏心距/m	最大弯矩/(kN·m)	最大偏心距/m	偏心距平方和/m²
本文方法	17.5	-0.002	-1 455.3	0.112	0.182
五点重合法	345.7	-0.030	-1 739.3	0.134	0.196
唐春艳^[19]的方法	-39.0	0.003	-1 415.0	0.109	0.186
任伟新等^[17]的方法	-23.6	0.002	-1 429.7	0.110	0.182
Lewis^[20]的方法	259.2	-0.021	-1 664.5	0.128	0.191
二次抛物线法	1 571.5	-0.136	-2 785.9	0.215	0.256

下载: 导出CSV

表 7 六种求解方法的特点比较

Table 7. Characteristic comparison of 6 solution methods

方法	计算精度	计算效率	计算难易程度	工程适用性	是否揭示了拱轴线的本质	拱桥初步设计阶段的适用性
本文方法	高	高	容易	适用	是	适用
五点重合法	较高	低	容易	较适用	否	较适用
唐春艳^[19]的方法	较高	高	容易	较适用	是	适用
任伟新等^[17]的方法	高	较高	较容易	适用	否	较适用
Lewis^[20]的方法	较高	较低	较难	较适用	否	不太适用
二次抛物线法	低	高	容易	不适用	否	较适用

下载: 导出CSV

参考文献(26)

[1]	BLOCK P, DEJONG M, OCHSENDORF J. As hangs the flexible line: equilibrium of masonry arches[J]. Nexus Network Journal, 2006, 8(2): 13-24. doi: 10.1007/s00004-006-0015-9
[2]	LEWIS W J, RUSSELL J M, LI T Q. Moment-less arches for reduced stress state. Comparisons with conventional arch forms[J]. Computers and Structures, 2021, 251: 106524. doi: 10.1016/j.compstruc.2021.106524
[3]	NIKOLI AC'G D. Catenary arch of finite thickness as the optimal arch shape[J]. Structural and Multidisciplinary Optimization, 2019, 60(5): 1957-1966. doi: 10.1007/s00158-019-02304-9
[4]	陈宝春, 刘君平. 世界拱桥建设与技术发展综述[J]. 交通运输工程学报, 2020, 20(1): 27-41. https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202001005.htm CHEN Bao-chun, LIU Jun-ping. Review of construction and technology development of arch bridges in the world[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 27-41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JYGC202001005.htm
[5]	ZHANG Guo-jing, LIU Yong-jian, ZHAO Wei, et al. Optimal arch shape of long-span open-spandrel arch bridges under vertical permanent loads[J]. Structures, 2022, 45: 1012-1030. doi: 10.1016/j.istruc.2022.09.086
[6]	侯春辉, 宋顺心. 基于APDL语言的拱轴线优化及立柱布置研究[J]. 铁道工程学报, 2017, 34(10): 55-59. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201710011.htm HOU Chun-hui, SONG Shun-xin. Research on the optimization of arch-axis and column layout based on APDL language[J]. Journal of Railway Engineering Society, 2017, 34(10): 55-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201710011.htm
[7]	宰国军, 周志祥. 钢箱砼组合拱桥的拱轴线优化算法研究[J]. 土木建筑与环境工程, 2014, 36(S1): 20-23. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN2014S1006.htm ZAI Guo-jun, ZHOU Zhi-xiang. Optimization algorithm research on the arch axis of steel box-concrete composite arch bridge[J]. Journal of Civil, Architectural and Environmental Engineering, 2014, 36(S1): 20-23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN2014S1006.htm
[8]	蒋启平. 三次样条插值确定拱桥合理拱轴线的方法探讨[J]. 武汉理工大学学报(交通科学与工程版), 2001, 25(1): 101-104. https://www.cnki.com.cn/Article/CJFDTOTAL-JTKJ200101027.htm JIANG Qi-ping. A study of method of determining rational arch axis using three ordersplin interpolation[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2001, 25(1): 101-104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JTKJ200101027.htm
[9]	罗辉. 一种新型的拱轴线及拱圈优化设计[J]. 桥梁建设, 1997, 27(2): 14-17. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS702.002.htm LUO Hui. Anew type of arch axis curve and optimization design of arch ring[J]. Bridge Construction, 1997, 27(2): 14-17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS702.002.htm
[10]	ZHANG Xue-song, LIANG Ning-yi, LU Xiao-hong, et al. Optimization method for solving the reasonable arch axis of long-span CFST arch bridges[J]. Advances in Civil Engineering, 2019, 2019: 7235656.
[11]	刘毓湘, 高敬红. 基于4次样条函数拱轴线优化设计的T-V求解法[J]. 公路交通科技, 2007, 24(6): 80-85. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200706018.htm LIU Yu-xiang, GAO Jing-hong. Topkis-Veinott feasible direction method for optimum axis of arch bridge based on quartic spline function[J]. Journal of Highway and Transportation Research and Development, 2007, 24(6): 80-85. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200706018.htm
[12]	范重, 胡纯炀, 刘先明, 等. 鄂尔多斯东胜体育场巨型拱索结构设计优化[J]. 建筑结构学报, 2016, 37(6): 9-18. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201606002.htm FAN Zhong, HU Chun-yang, LIU Xian-ming, et al. Optimized design of giant arch-cable structure of the Ordos Dongsheng Stadium[J]. Journal of Building Structures, 2016, 37(6): 9-18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201606002.htm
[13]	SHI Zhou, HU Hao, LI Jia-qi. Axis optimization of arch-shaped pylons for high-speed railway cable-stayed bridges[J]. Engineering Structures, 2021, 227: 111424.
[14]	NODARGI N A, BISEGNA P. Thrust line analysis revisited and applied to optimization of masonry arches[J]. International Journal of Mechanical Sciences, 2020, 179: 105690.
[15]	MICHIELS T, NAPOLITANO R, ADRIAENSSENS S, et al. Comparison of thrust line analysis, limit state analysis and distinct element modeling to predict the collapse load and collapse mechanism of a rammed earth arch[J]. Engineering Structures, 2017, 148: 145-156.
[16]	NIKOLICH D. Thrust line analysis of triangular arches[J]. Archive of Applied Mechanics, 2020, 90(9): 1861-1874.
[17]	任伟新, 胡常福, 上官兴, 等. 空腹式拱桥新型拱轴线研究[J]. 交通科学与工程, 2010, 26(2): 26-30, 47. https://www.cnki.com.cn/Article/CJFDTOTAL-CSJX201002006.htm REN Wei-xin, HU Chang-fu, SHANGGUAN Xing, et al. Research on new arch axis of open-spandrel arch bridge[J]. Journal of Transport Science and Engineering, 2010, 26(2): 26-30, 47. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSJX201002006.htm
[18]	胡常福, 廖妙星. 多源荷载作用下合理拱轴的近似解析[J]. 华东交通大学学报, 2018, 35(2): 46-55. https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201802007.htm HU Chang-fu, LIAO Miao-xing. Approximate analytical solution for rational arch axis under multi-type loads[J]. Journal of East China Jiaotong University, 2018, 35(2): 46-55. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201802007.htm
[19]	唐春艳. T构-系杆拱组合体系桥静力及动力性能研究[D]. 大连: 大连理工大学, 2018. TANG Chun-yan. Research on the static and dynamic characteristics of T-frame and tied arch composite bridge[D]. Dalian: Dalian University of Technology, 2018. (in Chinese)
[20]	LEWIS W J. Mathematical model of a moment-less arch[J]. Proceedings of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 2016, 472: 20160019.
[21]	GIL-MARTÍN L M, HERNÁNDEZ-MONTES E, PALOMARES A, et al. The optimum shape of an arch under non-symmetric loading conditions[J]. Archive of Applied Mechanics, 2016, 86(8): 1509-1520.
[22]	MARANO G C, TRENTADUE F, PETRONE F. Optimal arch shape solution under static vertical loads[J]. Acta Mechanica, 2014, 225(3): 679-686.
[23]	LEWIS W J. Constant stress arches and their design space[J]. Proceedings of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 2022, 478: 20210428.
[24]	陈宝春, 韦建刚, 周俊, 等. 我国钢管混凝土拱桥应用现状与展望[J]. 土木工程学报, 2017, 50(6): 50-61. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201706006.htm CHEN Bao-chun, WEI Jian-gang, ZHOU Jun, et al. Application of concrete-filled steel tube arch bridges in China: current status and prospects[J]. China Civil Engineering Journal, 2017, 50(6): 50-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201706006.htm
[25]	易云焜. 梁拱组合体系设计理论关键问题研究[D]. 上海: 同济大学, 2007. YI Yun-kun. Key problem study for design theory of beam-arch association bridges[D]. Shanghai: Tongji University, 2007. (in Chinese)
[26]	SALONGA J, GAUVREAU P. Comparative study of the proportions, form, and efficiency of concrete arch bridges[J]. Journal of Bridge Engineering, 2014, 19(3): 04013010.

施引文献

资源附件(0)

访问统计

点击查看大图

图(17) / 表(7)

计量

文章访问数: 529
HTML全文浏览量: 272
PDF下载量: 88
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

下承式拱桥合理拱轴线的解析解与计算方法

doi: 10.19818/j.cnki.1671-1637.2022.05.013

作者简介:
张国靖(1992-)，男，陕西榆林人，长安大学工学博士研究生，从事大跨桥梁结构研究

通讯作者:
刘永健(1966-)，男，江西玉山人，长安大学教授，工学博士

计量

Analytical solution and calculation method of reasonable arch axis of through arch bridge

Author Bio:
ZHANG Guo-jing (1992-), male, doctoral student, izhangguojing@126.com

LIU Yong-jian(1966-), male, professor, PhD, liuyongjian@chd.edu.cn

计量

目录

留言板

下承式拱桥合理拱轴线的解析解与计算方法

doi: 10.19818/j.cnki.1671-1637.2022.05.013

作者简介: 张国靖(1992-)，男，陕西榆林人，长安大学工学博士研究生，从事大跨桥梁结构研究

通讯作者: 刘永健(1966-)，男，江西玉山人，长安大学教授，工学博士

计量

出版历程

Analytical solution and calculation method of reasonable arch axis of through arch bridge

Author Bio: ZHANG Guo-jing (1992-), male, doctoral student, izhangguojing@126.com LIU Yong-jian(1966-), male, professor, PhD, liuyongjian@chd.edu.cn

计量

出版历程

目录

作者简介:
张国靖(1992-)，男，陕西榆林人，长安大学工学博士研究生，从事大跨桥梁结构研究

通讯作者:
刘永健(1966-)，男，江西玉山人，长安大学教授，工学博士

Author Bio:
ZHANG Guo-jing (1992-), male, doctoral student, izhangguojing@126.com

LIU Yong-jian(1966-), male, professor, PhD, liuyongjian@chd.edu.cn