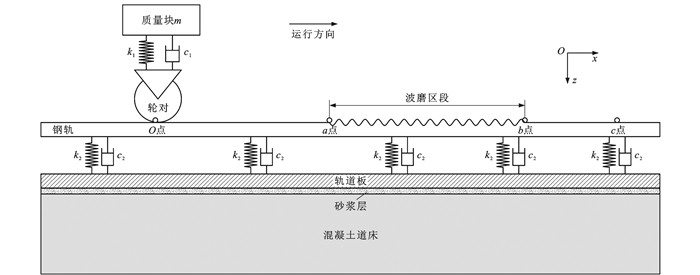
-
摘要: 为了探明轮轨垂向力与波磨状态之间的映射关系并采用轮轨力检测数据定量评价波磨严重程度，以中国CRTSⅡ高铁线路与服役动车组典型参数构建三维轮轨动力学有限元模型；细化波磨区段钢轨表面不平顺特征，采用高速综合检测列车在高铁波磨区段上实测轮轨垂向力时频数据验证有限元模型输出结果的准确性；模拟了车辆运行速度为300 km·h-1时波长在40~180 mm波磨激励下的轮轨垂向力，分析了其时频域分布特性；引入轨面不平顺变化率表征波磨沿钢轨纵向的变化特性，采用非线性最小二乘法与有理式方程拟合了不同波长条件下轮轨垂向力大值与轨面不平顺变化率之间的函数关系，分析了钢轨Pinned-Pinned固有共振频率及其半值振动模态对拟合参数曲线的影响，并推导了基于轮轨垂向力的波磨谷深估算方法；该谷深估算方法在某高铁线路波磨状态监测中初步试用，共发现32个波磨区段，并对比了波磨区段上实测谷深和估算谷深。分析结果表明：谷深估算值与实测值相关系数为0.97，两者具有较高的线性相关性；在谷深估算值大于0.08 mm时，估算值与实测值之间的均方根差约为0.01mm，基于谷深估算方法作出波磨打磨整治决策时的误判率约为6.25%，说明谷深估算方法在实际高铁线路上具有较好的适用性。Abstract: In order to find out the mapping relationship between wheel-rail vertical force and corrugation state and to evaluate quantitatively the severity of the corrugation by using wheel-rail force inspection data, the typical parameters from CRTS Ⅱ high-speed railway and electric multiple units in service in China were employed to construct a three-dimensional wheel-rail dynamics finite element model. The characteristics of the irregularities on the rail surface at the corrugation section were refined, and the simulation accuracy of the constructed model was verified by the time-frequency data of the measured wheel-rail vertical force from the high-speed comprehensive inspection car at the corrugation section in the high-speed railway. On this basis, the wheel-rail vertical forces excited by the corrugation with a wavelength between 40 mm and 180 mm at the running speed of 300 km·h-1 were simulated, and their distribution characteristics in time-frequency domain were analyzed. The change rate of rail surface irregularity was introduced to characterize the changing characteristics of the corrugation along the longitudinal direction of the rail. The nonlinear least square method and rational equation were used to fit the functional relationship between the large values of the wheel-rail vertical force and the change rates of rail surface irregularity under different wavelengths. The influence of rail vibration mode of the Pinned-Pinned natural resonant frequency and its half-value on the fitting parameter curves was analyzed. A method based on the wheel-rail vertical force was derived to estimate the valley depth of the corrugation. The valley depth estimation method was tentatively tested in the high-speed railway to evaluate the corrugation, 32 sets of corrugation sections were found, and the measured and estimated valley depths at the sections were compared. Analysis results show that the correlation coefficient between the estimated and measured valley depths is 0.97, so they have a high linear correlation. The root mean square error between the estimated and measured valley depths is approximately 0.01 mm when the estimated valley depth is greater than 0.08 mm, and the misjudgment rate in making decisions on rail grinding based on the estimated valley depth is approximately 6.25%, indicating that the estimation method of valley depth has good applicability in actual high-speed railway.
-
图 2 轮轨动力学模型实体单元构成与网格划分
Figure 2. Solid element composition and mesh of wheel-rail dynamics model
图 5 波磨区段轨面不平顺施加过程
Figure 5. Applied process of rail surface irregularity in corrugation section
图 8 波磨区段轨面不平顺实测的时频域特征
Figure 8. Measured time-frequency domain characteristics of rail surface irregularity in corrugation section
图 9 波磨区段实测轮轨垂向力与频谱
Figure 9. Measured wheel-rail vertical force and its spectrum in corrugation section
图 10 实测与仿真轮轨垂向力时频域曲线对比
Figure 10. Comparison of measured and simulated time-frequency domain curves of wheel-rail vertical force
图 11 不同工况下轮轨垂向力波形
Figure 11. Wheel-rail vertical force waveforms under different load cases
图 12 不同工况下轮轨垂向力大值与谷深关系曲线
Figure 12. Relation curves between large value of wheel-rail vertical force and valley depth under different load cases
图 13 波长为100 mm时轮轨垂向力与轮轨接触状态
Figure 13. Wheel-rail vertical force and contact state when wavelength is 100 mm
图 17 不同速度条件下c1随波长变化曲线
Figure 17. Changing curves of c1 with wavelength under different velocity conditions
图 18 轮轨垂向力、功率谱密度与附加轮轨垂向力
Figure 18. Wheel-rail vertical forces, power spectral densities and additional vertical forces
图 19 实测轨面不平顺与谷深累积曲线
Figure 19. Measured rail surface irregularity and valley depth accumulated curves
表 1 轮轨动力学模型主要参数
Table 1. Main parameters of wheel-rail dynamics model
参数名称 量值 参数名称 量值 轮轨材料 泊松比 0.30 一系悬挂弹簧(垂向) 刚度/(kN·mm-1) 1.04 密度/(mg·mm-3) 7.8 阻尼/(N·s·mm-1) 50.0 弹性模量/GPa 210.0 一系悬挂弹簧(横向) 刚度/(kN·mm-1) 0.40 切线模量/GPa 21.0 阻尼/(N·s·mm-1) 60.0 屈服强度/MPa 800.0 扣件支承弹簧(垂向) 刚度/(kN·mm-1) 22.00 轨道板 泊松比 0.25 阻尼/(N·s·mm-1) 47.7 密度/(mg·mm-3) 2.4 每米钢轨质量/kg 60.643 弹性模量/GPa 34.5 车体等部件等效质量/103 kg 14 CA砂浆材料 泊松比 0.20 混凝土道床材料 泊松比 0.16 密度/(mg·mm-3) 1.6 密度/(mg·mm-3) 2.4 弹性模量/GPa 8.0 弹性模量/GPa 32.5 静轮重P0/kN 70.3 轨枕间距Lr/mm 650.0 轮轨间摩擦因数 0.30 轮对滚动圆半径/mm 430 
下载: 导出CSV
表 2 不同波长下F-ξ拟合参数取值
Table 2. F-ξ fitting coefficient values under different
波长/mm c1/kN c2/kN d1 波长/mm c1/kN c2/kN d1 40 190.16 0.238 34 0.003 392 112 466.24 0.441 16 0.006 275 44 198.34 0.240 00 0.003 413 116 486.19 0.459 11 0.006 531 48 213.48 0.204 86 0.002 914 120 516.26 0.383 93 0.005 463 52 231.26 0.219 18 0.003 119 124 547.69 0.513 41 0.007 303 56 247.65 0.304 35 0.004 330 128 507.14 0.451 08 0.006 415 60 281.49 0.289 32 0.004 115 132 479.73 0.415 85 0.005 917 64 291.72 0.323 53 0.004 602 136 474.99 0.402 18 0.005 719 68 271.85 0.283 64 0.004 035 140 454.06 0.355 97 0.005 064 72 265.65 0.245 71 0.003 495 144 472.66 0.393 95 0.005 604 76 270.60 0.207 42 0.002 951 148 478.18 0.364 31 0.005 183 80 275.31 0.219 93 0.003 129 152 534.69 0.454 41 0.006 464 84 307.18 0.238 77 0.003 397 156 545.05 0.392 93 0.005 591 88 312.87 0.217 15 0.003 090 160 589.44 0.469 87 0.006 685 92 347.68 0.312 53 0.004 445 164 672.34 0.557 96 0.007 938 96 354.75 0.289 67 0.004 122 168 697.12 0.555 45 0.007 904 100 358.74 0.288 72 0.004 107 172 717.96 0.544 23 0.007 744 104 377.34 0.301 22 0.004 285 176 739.86 0.559 40 0.007 960 108 423.57 0.357 60 0.005 088 180 792.30 0.566 50 0.008 057
下载: 导出CSV
-
[1] GRASSIE S L, KALOUSEK J. Rail corrugation: characteristics, causes and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 57-68. doi: 10.1243/PIME_PROC_1993_207_227_02 [2] GRASSIE S L. Rail corrugation: advances in measurement, understanding and treatment[J]. Wear, 2005, 258(7/8): 1224-1234. [3] GRASSIE S L. Rail corrugation: characteristics, causes, and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(6): 581-596. doi: 10.1243/09544097JRRT264 [4] 金学松, 李霞, 李伟, 等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报, 2016, 51(2): 264-273. doi: 10.3969/j.issn.0258-2724.2016.02.006JIN Xue-song, LI Xia, LI Wei, et al. Review of rail corrugation progress[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 264-273. (in Chinese) doi: 10.3969/j.issn.0258-2724.2016.02.006 [5] CHEN G X, ZHOU Z R, OUYANG H, et al. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset-track system[J]. Journal of Sound and Vibration, 2010, 329(22): 4643-4655. doi: 10.1016/j.jsv.2010.05.011 [6] CUI Xiao-lu, HE Zhi-qiang, HUANG Bo, et al. Study on the effects of wheel-rail friction self-excited vibration and feedback vibration of corrugated irregularity on rail corrugation[J]. Wear, 2021, 477: 203854. doi: 10.1016/j.wear.2021.203854 [7] BELLETTE P A, MEEHAN P A, DANIEL W J T. Effects of variable pass speed on wear-type corrugation growth[J]. Journal of Sound and Vibration, 2008, 314(3/4/5): 616-634. [8] SUDA Y, KOMINE H, MATSUMOTO K, et al. Feedback friction control between wheel and rail by detecting yaw moment of wheelset[J]. Wear, 2008, 265(9/10): 1512-1517. [9] KURZECK B. Combined friction induced oscillations of wheelset and track during the curving of metros and their influence on corrugation[J]. Wear, 2011, 271(1/2): 299-310. [10] WU T X. Effects on short pitch rail corrugation growth of a rail vibration absorber/damper[J]. Wear, 2011, 271(1/2) : 339-348. [11] GAZAFRUDI S M M, YOUNESIAN D, TORABI M. A high accuracy and high speed imaging and measurement system for rail corrugation inspection[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8894-8903. doi: 10.1109/TIE.2020.3013748 [12] THOMAS H M, HECKEL T, HANSPACH G. Advantage of a combined ultrasonic and eddy current examination for railway inspection trains[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2007, 49 (6): 341-344. doi: 10.1784/insi.2007.49.6.341 [13] HAIGERMOSER A, LUBER B, RAUH J, et al. Road and track irregularities: measurement, assessment and simulation[J]. Vehicle System Dynamics, 2015, 53(7): 878-957. doi: 10.1080/00423114.2015.1037312 [14] BOCCIOLONE M, CAPRIOLI A, CIGADA A, et al. A measurement system for quick rail inspection and effective track maintenance strategy[J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1242-1254. doi: 10.1016/j.ymssp.2006.02.007 [15] SALVADOR P, NARANJO V, INSA R, et al. Axlebox accelerations: their acquisition and time-frequency characterisation for railway track monitoring purposes[J]. Measurement, 2016, 82: 301-312. doi: 10.1016/j.measurement.2016.01.012 [16] BAGHERI V R, YOUNESIAN D, TEHRANI P H. A new methodology for the estimation of wheel-rail contact forces at a high-frequency range[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(10): 2353-2370. doi: 10.1177/0954409718771746 [17] MAGLIO M, VERNERSSON T, NIELSEN J C O, et al. Railway wheel tread damage and axle bending stress- Instrumented wheelset measurements and numerical simulations[J]. International Journal of Rail Transportation, 2022, 10(3): 275-297. doi: 10.1080/23248378.2021.1932621 [18] NIELSEN J C O. High-frequency vertical wheel-rail contact forces-validation of a prediction model by field testing[J]. Wear, 2008, 265(9/10): 1465-1471. http://www.onacademic.com/detail/journal_1000034597136410_1228.html [19] NIELSEN J C O. Rail roughness level assessment based on high-frequency wheel-rail contact force measurements[C]//Springer. Proceedings of the 9th International Workshop on Railway Noise. Berlin: Springer, 2008: 355-362. [20] GULLERS P, ANDERSSON L, LUNDÉN R. High-frequency vertical wheel-rail contact forces—field measurements and influence of track irregularities[J]. Wear, 2008, 265(9/10): 1472-1478. [21] 李谷, 张志超, 祖宏林, 等. 高速铁路典型轨道病害下轮轨力响应特性试验研究[J]. 中国铁道科学, 2019, 40(6): 30-36. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201906005.htmLI Gu, ZHANG Zhi-chao, ZU Hong-lin, et al. Experimental study on wheel-rail force response characteristics under typical track defects of high speed railway[J]. China Railway Science, 2019, 40(6): 30-36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201906005.htm [22] 牛留斌, 李谷, 刘金朝, 等. 轮轨力在轨道短波不平顺检测中的应用[J]. 铁道建筑, 2019, 59(8): 133-139. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201908032.htmNIU Liu-bin, LI Gu, LIU Jin-zhao, et al. Application of the wheel-rail force in track short wave irregularity detection[J]. Railway Engineering, 2019, 59(8): 133-139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201908032.htm [23] AFFERRANTE L, CIAVARELLA M. Short-pitch rail corrugation: a possible resonance-free regime as a step forward to explain the "enigma"?[J]. Wear, 2009, 266(9/10): 934-944. [24] 李伟, 曾全君, 朱士友, 等. 地铁钢轨波磨对车辆和轨道动态行为的影响[J]. 交通运输工程学报, 2015, 15(1): 34-42. doi: 10.19818/j.cnki.1671-1637.2015.01.005LI Wei, ZENG Quan-jun, ZHU Shi-you, et al. Effect of metro rail corrugation on dynamic behaviors of vehicle and track[J]. Journal of Traffic and Transportation Engineering, 2015, 15(1): 34-42. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2015.01.005 [25] TORSTENSSON P T, NIELSEN J C O, BAEZA L. High- frequency vertical wheel-rail contact forces at high vehicle speeds-the influence of wheel rotation[C]//Springer. Proceedings of the 10th International Workshop on Railway Noise. Berlin: Springer, 2012: 43-50. [26] IDÁRRAGA ALARCÓN G, BURGELMAN N, MEZA J M, et al. Power dissipation modeling in wheel/rail contact: effect of friction coefficient and profile quality[J]. Wear, 2016, 366/367: 217-224. doi: 10.1016/j.wear.2016.04.026 [27] ESVELD C. Modern Railway Track[M]. Duisburg: MRT Productions, 2001. [28] BAEK K S, KYOGOKU K, NAKAHARA T. An experimental study of transient traction characteristics between rail and wheel under low slip and low speed conditions[J]. Wear, 2008, 265(9/10): 1417-1424. [29] BELYTSCHKO T, LIU W K, MORAN B. Nonlinear Finite Elements for Continua and Structures[M]. New York: John Wiley, 2000. [30] TSAI H C, WANG C Y, HUANG N E, et al. Railway track inspection based on the vibration response to a scheduled train and the Hilbert-Huang transform[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2015, 229(7): 815-829. doi: 10.1177/0954409714527930 [31] MADSEN K, NIELSEN H B, TINGLEFF O. Methods for Non-Linear Least Square Problems[M]. Kongens Lyngby: Technical University of Denmark, 2004. [32] MAN A P D. A survey of dynamic railway track properties and their quality[D]. Delft: Delft University of Technology, 2002. [33] FANG Ge, WANG Yu-rong, PENG Zhi-ke, et al. Theoretical investigation into the formation mechanism and mitigation measures of short pitch rail corrugation in resilient tracks of metros[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(9): 2260-2271. [34] CAPRIOLI A, CIGADA A, RAVEGLIA D. Rail inspection in track maintenance: a benchmark between the wavelet approach and the more conventional Fourier analysis[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 631-652. -
点击查看大图
计量
- 文章访问数: 445
- HTML全文浏览量: 242
- PDF下载量: 93
- 被引次数: 0
