Stiffness characteristics and life prediction of rail pads of subway damping fasteners
Article Text (Baidu Translation)
-
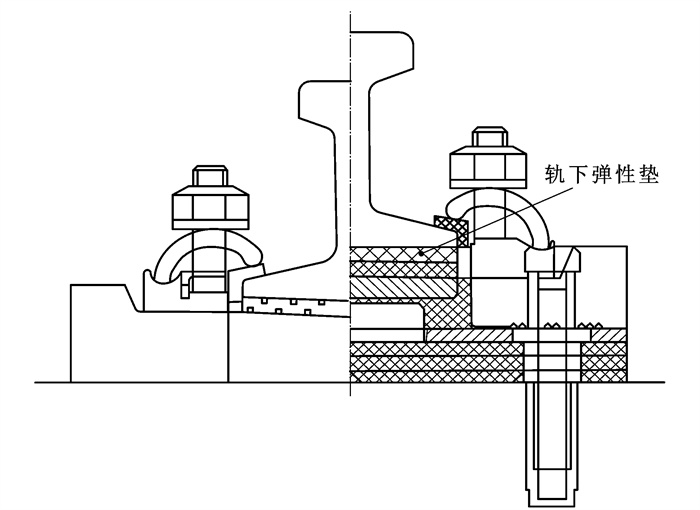
摘要: 为了研究地铁减振扣件弹性垫在服役过程中刚度敏感性和对线路环境振动的影响，以南京地铁多条运营线路中抽取的压缩型减振扣件为研究对象，开展了压缩型扣件轨下弹性垫服役刚度特性、常温下疲劳特性和热加速疲劳老化特性等多环境室内综合测试；基于测试结果对比分析了新旧压缩型扣件轨下弹性垫使用时间与刚度变化的相关性，得到了轨下弹性垫的时间-寿命特性曲线，提出了轨下弹性垫刚度变化百分比与使用时间的寿命预测模型。研究结果表明：在周期性轮轨载荷和线路温湿碱环境等综合作用下，地铁减振扣件轨下弹性垫的服役刚度随使用时间呈线性增加趋势，其弹性发生了性能退化；新的轨下弹性垫热加速疲劳老化刚度曲线与服役抽样轨下弹性垫的刚度曲线趋势基本一致，即轨下弹性垫的热加速循环老化试验能够模拟或演化轨道交通线路的热机械循环载荷等现场条件；基于Arrhenius寿命-应力热加速老化模型，轨下弹性垫服役应力和加速老化应力下的加速因子分别为1.99和1.36，进而可通过加速因子预测减振扣件轨下弹性垫的更换周期。Abstract: In order to study the stiffness sensitivity of rail pads of subway damping fasteners in service and their influence on line environmental vibration, the compression-type damping fasteners extracted from several operating lines of Nanjing Metro were taken as the research object, and the multi-environmental indoor comprehensive tests of the stiffness characteristics, fatigue characteristics at room temperature, and thermal accelerated fatigue aging characteristics of rail pads of the compression-type fasteners in service were carried out. Based on the test results, the correlations between service time and stiffness change of rail pads of new and old compression-type fasteners were compared and analyzed. The time-life characteristic curves of rail pads were obtained, and the life prediction model for the percentage change in stiffness and service time of the rail pads was proposed. Research results indicate that under the combined effect of periodic wheel-rail loads and the temperature, humidity, and alkaline environment of the line, the service stiffness of rail pads of the subway damping fasteners increases linearly with service time, and the elasticity of rail pads undergoes performance degradation. The stiffness curve trend of the new rail pads under thermal accelerated fatigue aging is basically consistent with the stiffness curve trend of the sampled rail pads in service. In other words, the thermal accelerated cyclic aging test of the rail pads can simulate or evolve on-site conditions such as the thermal mechanical cyclic load of the line. Based on the Arrhenius life-stress thermal accelerated aging model, the acceleration factors of rail pads under service stress and accelerated aging stress are 1.99 and 1.36, respectively, which can be used to predict the replacement cycle of rail pads of the damping fasteners.
-
图 7 轨下弹性垫动静刚度比随使用时间变化曲线
Figure 7. Curve of stiffness ratio with service time of rail pad
图 8 扣件与轨下弹性垫刚度随使用时间关系
Figure 8. Relationships between stiffness and service time of fastener and rail pad
图 9 轨下弹性垫高温下时间与刚度关系
Figure 9. Relationship between time and stiffness of rail pad at high temperature
图 12 热加速疲劳老化循环次数与刚度关系
Figure 12. Relationship between thermal accelerated fatigue aging cycles and stiffness
图 13 刚度变化率与循环次数、使用时间关系
Figure 13. Rate of stiffness change in relation to cycles and service time
表 1 试验方法与参数
Table 1. Test methods and parameters
试验方法 样件类型 服役时间/月 试验类型 数量/件 载荷参数 1 线路垫板 24~66 动静刚度 3 每天388列，15万人次 2 新垫板 0 静态刚度 3 割线静刚度载荷为15、45 kN 3 新垫板 0 加热静刚度 3 割线静刚度载荷为15、45 kN，周期为30 d，温度为80 ℃ 4 新垫板 0 常温循环疲劳 3 疲劳幅值为8~45 kN，加载频率为4 Hz，循环次数为6.0×106 5 新垫板 0 热加速疲劳老化 3 温度为80 ℃，加载频率为4 Hz，循环次数为6.0×106，刚度取值为15、45 kN 
下载: 导出CSV
-
[1] 程保青, 杨其振, 刘道通. 城轨交通新型轨道扣件研究与设计[J]. 铁道工程学报, 2012, 29(4): 90-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201204018.htmCHENG Bao-qing, YANG Qi-zhen, LIU Dao-tong. The research and design of a new type fastening for urban rail transit[J]. Journal of Railway Engineering Society, 2012, 29(4): 90-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201204018.htm [2] 张皓迪, 何远鹏, 王星欢, 等. 地铁轨道扣件和减振垫参数的减振性能最优匹配[J]. 中南大学学报(自然科学版), 2022, 53(6): 2382-2392. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202206037.htmZHANG Hao-di, HE Yuan-peng, WANG Xing-huan, et al. Optimal matching for vibration reduction of parameters of track fastener and rubber absorber of metro[J]. Journal of Central South University (Science and Technology), 2022, 53(6): 2382-2392. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202206037.htm [3] 孙旭, 王平. 高速铁路扣件失效对车辆-轨道耦合系统动态响应的影响[J]. 铁道学报, 2022, 44(8): 108-116. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202208012.htmSUN Xu, WANG Ping. Effect of fastener failure of high-speed railway on dynamic response of vehicle-track coupling system[J]. Journal of the China Railway Society, 2022, 44(8): 108-116. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202208012.htm [4] CARRASCAL I A, CASADO J A, POLANCO J A, et al. Dynamic behaviour of railway fastening setting pads[J]. Engineering Failure Analysis, 2007, 14(2): 364-373. doi: 10.1016/j.engfailanal.2006.02.003 [5] 罗惠峰, 石广田, 张小安, 等. 轨下垫板参数对轨道结构垂向振动影响研究[J]. 兰州交通大学学报, 2019, 38(1): 88-94. https://www.cnki.com.cn/Article/CJFDTOTAL-LZTX201901014.htmLUO Hui-feng, SHI Guang-tian, ZHANG Xiao-an, et al. Influences of rail pads parameters on vertical vibration of track structure[J]. Journal of Lanzhou Jiaotong University, 2019, 38(1): 88-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LZTX201901014.htm [6] SAINZ-AJA J A, CARRASCAL I A, FERREÑO D, et al. Influence of the operational conditions on static and dynamic stiffness of rail pads[J]. Mechanics of Materials, 2020, 148: 103505. doi: 10.1016/j.mechmat.2020.103505 [7] 韦凯, 王丰, 赵泽明, 等. 弹性分开式扣件弹性垫板静刚度测试评价方法[J]. 铁道工程学报, 2018, 35(11): 32-36, 86. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201811006.htmWEI Kai, WANG Feng, ZHAO Ze-ming, et al. The methodology research on the test and evaluation of static stiffness of rail pads in elastic separated fastener[J]. Journal of Railway Engineering Society, 2018, 35(11): 32-36, 86. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201811006.htm [8] GAO Xiao-gang, FENG Qing-song, WANG An-bin, et al. Testing research on frequency-dependent characteristics of dynamic stiffness and damping for high-speed railway fastener[J]. Engineering Failure Analysis, 2021, 129: 105689. doi: 10.1016/j.engfailanal.2021.105689 [9] 吴昊, 王安斌, 高晓刚. 预压荷载、板下材质、螺栓扭矩和频率对扣件系统刚度特性影响研究[J]. 铁道标准设计, 2022, 66(9): 69-73. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202209012.htmWU Hao, WANG An-bin, GAO Xiao-gang. Study on the influence of preload, material under plate, bolt torque and frequency on the stiffness characteristics of fastener system[J]. Railway Standard Design, 2022, 66(9): 69-73. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202209012.htm [10] 赵俊康, 王安斌, 高晓刚, 等. 双层非线性减振扣件刚度及其影响因素研究[J]. 铁道标准设计, 2020, 64(5): 62-67. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202005011.htmZHAO Jun-kang, WANG An-bin, GAO Xiao-gang, et al. Study on performances of a double-layer nonlinear vibration-damping fastener[J]. Railway Standard Design, 2020, 64(5): 62-67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS202005011.htm [11] 胡连军, 杨吉忠, 林红松, 等. 钢轨扣件设计及其衍化过程研究[J]. 铁道工程学报, 2018, 35(10): 32-37. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201810007.htmHU Lian-jun, YANG Ji-zhong, LIN Hong-song, et al. Research on the rail fastening design and its derivation process[J]. Journal of Railway Engineering Society, 2018, 35(10): 32-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201810007.htm [12] 朱海燕, 袁遥, 肖乾, 等. 钢轨波磨研究进展[J]. 交通运输工程学报, 2021, 21(3): 110-133. doi: 10.19818/j.cnki.1671-1637.2021.03.006ZHU Hai-yan, YUAN Yao, XIAO Qian, et al. Research progress on rail corrugation[J]. Journal of Traffic and Transportation Engineering, 2021, 21(3): 110-133. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2021.03.006 [13] 张帆, 王志强, 王金朝, 等. 钢轨波磨对地铁轨道振动特性影响研究[J]. 噪声与振动控制. 2022, 42(3): 182-186. https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK202203032.htmZHANG Fan, WANG Zhi-qiang, WANG Jin-zhao, et al. Study on the influence of rail wave grinding on vibration characteristics of metro tracks[J]. Noise and Vibration Control, 2022, 42(3): 182-186. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK202203032.htm [14] EGANA J I, VINOLAS J, SECO M. Investigation of the influence of rail pad stiffness on rail corrugation on a transit system[J]. Wear, 2006, 261(2): 216-224. [15] OREGUI M, DE MAN A, WOLDEKIDAN M F, et al. Obtaining railpad properties via dynamic mechanical analysis[J]. Journal of Sound and Vibration, 2016, 363: 460-472. [16] 刘林芽, 崔巍涛, 秦佳良, 等. 扣件胶垫黏弹性对铁路箱梁振动与结构噪声的影响[J]. 交通运输工程学报, 2021, 21(3): 134-145. doi: 10.19818/j.cnki.1671-1637.2021.03.007LIU Lin-ya, CUI Wei-tao, QIN Jia-liang, et al. Effects of rail pad viscoelasticity on vibration and structure-borne noise of railway box girder[J]. Journal of Traffic and Transportation Engineering, 2021, 21(3): 134-145. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2021.03.007 [17] 韦凯, 王丰, 杨麒陆, 等. 钢轨扣件弹性垫板的宽频动力性能及其理论表征[J]. 铁道学报, 2019, 41(2): 130-136. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201902019.htmWEI Kai, WANG Feng, YANG Qi-lu, et al. Broad frequency-domain dynamic properties of rail pad and its theoretical model[J]. Journal of the China Railway Society, 2019, 41(2): 130-136. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201902019.htm [18] 韦凯, 赵泽明, 欧灵畅, 等. WJ-8型扣件弹性垫板低温动力性能及其影响研究[J]. 铁道工程学报, 2018, 35(3): 31-37. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201803006.htmWEI Kai, ZHAO Ze-ming, OU Ling-chang, et al. Research on the dynamic properties of rail pad for WJ-8 fastener at low temperatures and its influence on vehicle-track coupled system[J]. Journal of Railway Engineering Society, 2018, 35(3): 31-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201803006.htm [19] 陈宗平, 成功, 刘清源, 等. 高速铁路扣件动刚度频变和温变特性研究[J]. 振动、测试与诊断, 2022, 42(3): 495-502, 616-617. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS202203012.htmCHEN Zong-ping, CHENG Gong, LIU Qing-yuan, et al. A study on the frequency and temperature-dependences of the dynamic stiffness of fasteners used on high-speed railways[J]. Journal of Vibration, Measurement and Diagnosis, 2022, 42(3): 495-502, 616-617. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS202203012.htm [20] 张攀, 周昌盛, 王平. 轨下垫板刚度的时变特性及其影响研究[J]. 铁道标准设计, 2015, 59(9): 49-52. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201509013.htmZHANG Pan, ZHOU Chang-sheng, WANG Ping. Study on time variant characteristics and effects of rail pad stiffness[J]. Railway Standard Design, 2015, 59(9): 49-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS201509013.htm [21] 蒋林宏, 李科委, 马宇飞. 南京地铁扣件的典型伤损及使用性能分析[J]. 铁道建筑, 2021, 61(7): 155-159. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202107034.htmJIANG Lin-hong, LI Ke-wei, MA Yu-fei. Typical damage and performance analysis of fastener in Nanjing metro[J]. Railway Engineering, 2021, 61(7): 155-159. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202107034.htm [22] WEI Kai, YANG Qi-lu, DOU Yin-ling, et al. Experimental investigation into temperature- and frequency-dependent dynamic properties of high-speed rail pads[J]. Construction and Building Materials, 2017, 151: 848-858. [23] 王绍华, 韦凯, 杨敏婕, 等. 扣件胶垫频变动力性能对钢轨垂向振动特性影响分析[J]. 铁道科学与工程学报, 2019, 16(4): 892-899. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201904008.htmWANG Shao-hua, WEI Kai, YANG Min-jie, et al. Influence of frequency-dependent dynamic properties of rail pad on vertical vibration characteristics of rail[J]. Journal of Railway Science and Engineering, 2019, 16(4): 892-899. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201904008.htm [24] LI Qi, DAI Bao-rui, ZHU Zhi-hui, et al. Improved indirect measurement of the dynamic stiffness of a rail fastener and its dependence on load and frequency[J]. Construction and Building Materials, 2021, 304: 124588. [25] ZHU Sheng-yang, CAI Cheng-biao, SPANOS P D. A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab track systems[J]. Journal of Sound and Vibration, 2015, 335: 304-320. [26] XU Jing-mang, WANG Kai, LIANG Xin-yuan, et al. Influence of viscoelastic mechanical properties of rail pads on wheel and corrugated rail rolling contact at high speeds[J]. Tribology International, 2020, 151: 106523. [27] 韦凯, 张攀, 王平. 扣件胶垫刚度的幅频变对轮轨耦合系统随机频响特征的影响[J]. 工程力学, 2017, 34(4): 108-115. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201704014.htmWEI Kai, ZHANG Pan, WANG Ping. Influence of amplitude- and frequency-dependent stiffness of rail pads on the frequency-domain random vibration of vehicle-track coupled system[J]. Engineering Mechanics, 2017, 34(4): 108-115. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201704014.htm [28] FERREÑO D, SAINZ-AJA J A, CARRASCAL I A, et al. Prediction of mechanical properties of rail pads under in-service conditions through machine learning algorithms[J]. Advances in Engineering Software, 2021, 151: 102927. [29] 凡艳丽, 张远庆, 于毫勇. 基于加速老化试验的高速铁路用橡胶垫板老化寿命预测[J]. 铁道建筑, 2021, 61(2): 117-120. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202102028.htmFAN Yan-li, ZHANG Yuan-qing, YU Hao-yong. Aging life prediction of rubber pads for high speed railway based on accelerated aging test[J]. Railway Engineering, 2021, 61(2): 117-121. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202102028.htm [30] SUNG D, HONG S. A simple method to assess replacement period of polyurethane railpad in urban railway[J]. Construction and Building Materials, 2020, 248: 118607. [31] 黄文斌, 孙炎, 吴明明, 等. 聚氨酯高温老化性能研究及寿命评估[J]. 聚氨酯工业, 2022, 37(5): 43-46. https://www.cnki.com.cn/Article/CJFDTOTAL-JAZG202205012.htmHUANG Wen-bin, SUN Yan, WU Ming-ming, et al. Research on thermal aging and lifetime evaluation of polyurethane[J]. Polyurethane Industry, 2022, 37(5): 43-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JAZG202205012.htm -
点击查看大图
图(13) / 表(1)
计量
- 文章访问数: 671
- HTML全文浏览量: 309
- PDF下载量: 102
- 被引次数: 0
