柔性路面结构设计的动力安定下限理论与分析方法

钱建固; 戴浴晨

doi:10.19818/j.cnki.1671-1637.2023.04.003

柔性路面结构设计的动力安定下限理论与分析方法

doi: 10.19818/j.cnki.1671-1637.2023.04.003

钱建固^{1, 2,},
戴浴晨^{1, 2}

1.
同济大学土木工程学院，上海 200092
2.
同济大学岩土及地下工程教育部重点实验室，上海 200092

基金项目:

国家自然科学基金项目 51578413

中央高校基本科研业务费专项资金项目 20232ZD08

详细信息

作者简介:
钱建固(1972-)，男，安徽无为人，同济大学教授，工学博士，从事岩土工程研究

中图分类号: U416
计量
- 文章访问数: 612
- HTML全文浏览量: 165
- PDF下载量: 114
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-05
- 网络出版日期: 2023-09-08
- 刊出日期: 2023-08-25

Theory and analysis method of lower-bound dynamic shakedown for design of flexible pavement structure

QIAN Jian-gu^{1, 2
,},
DAI Yu-chen^{1, 2}

1.
College of Civil Engineering, Tongji University, Shanghai 200092, China
2.
Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China

Funds:

National Natural Science Foundation of China 51578413

Fundamental Research Funds for the Cnetral Universities 20232ZD08

More Information

Author Bio:
QIAN Jian-gu(1972-), male, professor, PhD, qianjiangu@tongji.edu.cn

摘要

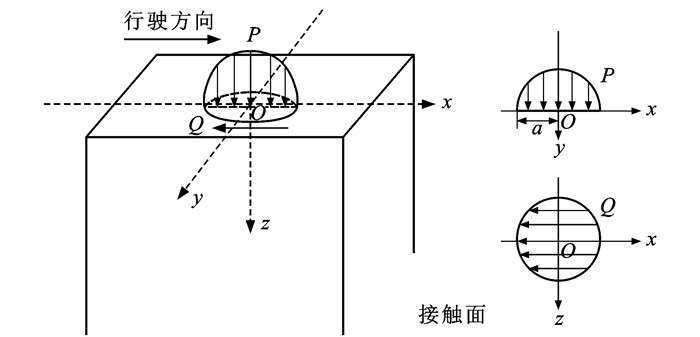
摘要: 为研究长期交通荷载作用下柔性路面路基的力学响应与服役性能，回顾了安定理论在柔性路面路基设计过程中的研究现状、存在问题及前沿进展，阐释了经典上限、下限动力安定理论的基本原理及其在交通岩土工程领域的应用与发展现状，阐述了下限安定的判别准则与数值分析方法；结合人工边界-动力有限元案例揭示了交通移动荷载作用下路面-路基系统的动力响应，讨论了材料横观各向同性、轮-路摩擦等因素对道路结构动力安定性的影响规律。分析结果表明：交通荷载作用下道路结构的动力效应对安定极限有重要影响，下限安定极限水平随车辆移动速度的增大而降低，当移动速度增至结构体系的Rayleigh波速时，道路结构体系的安定极限降至最低；路基材料力学属性与各向异性程度、轮-路摩擦因数等因素对柔性道路结构的下限动力安定极限也有重要影响；道路结构体系的下限动力安定极限随结构上层与下层弹性模量比的增加先增大后减小；对应最大安定极限的最优模量比表明安定极限临界位置从下层路基向上层路面的转变；考虑水平向摩擦时，轮-路摩擦因数的增大会明显降低结构的动力安定极限，同时减弱荷载移动速度对道路结构动力效应的影响。
- 路面工程 /
- 动力安定下限 /
- 有限元模拟 /
- 荷载移动速度 /
- 横观各向同性 /
- 摩擦因数
Abstract: To study the mechanical response and service performance of flexible pavement subgrades under long-term traffic loads, the current research state, existing issues, and frontier of the shakedown theorem in the design process of flexible pavement subgrades were reviewed. The basic principles of classical upper- and lower-bound dynamic shakedown theorem and their application and development in transportation geotechnics were introduced. The critical criterion and numerical analysis method of lower-bound shakedown were discussed in detail. Based on the case studied by the dynamic finite elements within artificial boundaries, the dynamic responses of pavement-subgrade system under the traffic moving loads were revealed. The effects of cross-anisotropic materials and wheel-pavement friction on the dynamic shakedown of the road structure were discussed. Research results show that the dynamic responses of the road structure under the traffic load are significant for the shakedown limit. The lower-bound shakedown limit level reduces with the growing traffic moving speed and reaches the minimum value when the moving speed approaches around the Rayleigh wave velocity of the structure system. The material mechanical properties of subgrade, the degree of anisotropy, as well as the wheel-pavement friction coefficient may also produce considerable effects on the lower-bound dynamic shakedown limit of the flexible road structure. The lower-bound dynamic shakedown limit of the road structure system increases at first and then decreases with the increase in the elastic modulus ratio of the upper and lower layers of the structure. The optimal modulus ratio corresponding to the maximum shakedown limit indicates that the critical position of the shakedown limit changes from the lower subgrade to the upper pavement. When the horizontal friction is considered, the increase in the wheel-pavement friction coefficient will obviously reduce the dynamic shakedown limit of the structure and weaken the influence of moving load speed on the dynamic response of the road structure.
- pavement engineering /
- lower-bound dynamic shakedown /
- finite element simulation /
- load moving speed /
- cross-anisotropic /
- friction coefficient

HTML全文

图 1 道路三维理想模型示意

Figure 1. Schematic of idealized 3D road model

下载: 全尺寸图片幻灯片

图 2 无限元边界有限元模型

Figure 2. Finite element model with infinite element boundary

下载: 全尺寸图片幻灯片

图 3 模拟竖向和水平向体力加载的薄层单元

Figure 3. Thin-layered elements modeling vertical and horizontal body forces

下载: 全尺寸图片幻灯片

图 4 下限安定极限计算流程

Figure 4. Calculation process of lower limit of shakedown limit

下载: 全尺寸图片幻灯片

图 5 不同荷载移动速度下的轴向动应力分布

Figure 5. Distributions of axial dynamic stresses at different load moving speeds

下载: 全尺寸图片幻灯片

图 6 数值计算结果与解析解的对比

Figure 6. Comparison between numerical and analytical results

下载: 全尺寸图片幻灯片

图 7 低速状态计算结果与静力解的对比

Figure 7. Comparison between low speed solution and static solution

下载: 全尺寸图片幻灯片

图 8 安定极限随摩擦因数的变化

Figure 8. Variations of shakedown limit with friction coefficient

下载: 全尺寸图片幻灯片

图 9 荷载移动速度对动力安定极限的影响

Figure 9. Effects of load moving speed on dynamic shakedown limits

下载: 全尺寸图片幻灯片

图 10 路基弹性模量对动力安定极限的影响

Figure 10. Effect of elastic modulus of subgrade on dynamic shakedown limits

下载: 全尺寸图片幻灯片

图 11 双层道路简化模型

Figure 11. Simplified model of two-layered road

下载: 全尺寸图片幻灯片

图 12 不同荷载移动速度下安定极限随弹性模量比的变化

Figure 12. Variations of shakedown limit with elastic modulus ratio under different load moving speeds

下载: 全尺寸图片幻灯片

图 13 低速状态计算结果与静力解的对比

Figure 13. Comparison between low speed solution and static solution

下载: 全尺寸图片幻灯片

图 14 不同强度比时安定极限与荷载移动速度的关系

Figure 14. Relationships between shakedown limit and load moving speed under different strength ratios

下载: 全尺寸图片幻灯片

图 15 不同各向异性模量比下的安定极限(v=70 m·s^-1，E_v2/E_h2=0.25)

Figure 15. Shakedown limits under different anisotropic modulus ratios (v=70 m·s^-1, E_v2/E_h2=0.25)

下载: 全尺寸图片幻灯片

图 16 不同摩擦因数下安定极限随荷载移动速度的变化

Figure 16. Variations of shakedown limits with load moving speeds under different friction coefficients

下载: 全尺寸图片幻灯片

图 17 不同荷载移动速度下轮-路摩擦因数对安定极限的影响(φ=30°)

Figure 17. Influences of wheel-road friction coefficient on shakedown limit under different load moving speeds (φ=30°)

下载: 全尺寸图片幻灯片

图 18 不同强度比下安定极限与弹性模量比的关系(v= 40 m·s^-1)

Figure 18. Relationships between shakedown limit and elastic modulus ratio under different strength ratios (v=40 m·s^-1)

下载: 全尺寸图片幻灯片

表 1 双层道路结构的材料参数

Table 1. Material parameters of two-layered road structure

结构层	弹性模量/ MPa	泊松比	密度/ (kg·m^-3)	内摩擦角/ (°)
第1层	20~20 000	0.25	2 200	30
第2层	20	0.48	1 800	0

下载: 导出CSV

参考文献(71)

[1]	RAZOUKI S S, EL-JANABI O A. Decrease in the CBR of a gypsiferous soil due to long-term soaking[J]. Quarterly Journal of Engineering Geology, 1999, 32(1): 87-89. doi: 10.1144/GSL.QJEG.1999.032.P1.07
[2]	RAZOUKI S S, KUTTAH D K. Predicting long-term soaked CBR of gypsiferous subgrade soils[J]. Proceedings of the Institution of Civil Engineers-Transport, 2006, 159(3): 135-140. doi: 10.1680/tran.2006.159.3.135
[3]	THAKUR J K, HAN Jie, POKHAREL S K, et al. Performance of geocell-reinforced recycled asphalt pavement (RAP) bases over weak subgrade under cyclic plate loading[J]. Geotextiles and Geomembranes, 2012, 35: 14-24. doi: 10.1016/j.geotexmem.2012.06.004
[4]	FAROOQ K, MUJTABA H. Prediction of California bearing ratio (CBR) and compaction characteristics of granular soils[J]. Acta Geotechnica Slovenica, 2017, 14(1): 62-72.
[5]	ALI H A, TAYABJI S D, LA TORRE F. Calibration of mechanistic-empirical rutting model for in-service pavements[J]. Transportation Research Record, 1998(1629): 159-168.
[6]	COOPER S B, ELSEIFI M, MOHAMMAD L N, et al. Performance and cost-effectiveness of sustainable technologies in flexible pavements using the mechanistic-empirical pavement design guide[J]. Journal of Materials in Civil Engineering, 2012, 24(2): 239-247. doi: 10.1061/(ASCE)MT.1943-5533.0000376
[7]	PEREIRA P, PAIS J. Main flexible pavement and mix design methods in Europe and challenges for the development of an European method[J]. Journal of Traffic and Transportation Engineering (English Edition), 2017, 4(4): 316-346. doi: 10.1016/j.jtte.2017.06.001
[8]	MALLA R B, JOSHI S. Subgrade resilient modulus prediction models for coarse and fine-grained soils based on long-term pavement performance data[J]. International Journal of Pavement Engineering, 2008, 9(6): 431-444. doi: 10.1080/10298430802279835
[9]	LEE J, KIM J, KANG B. Normalized resilient modulus model for subbase and subgrade based on stress-dependent modulus degradation[J]. Journal of Transportation Engineering, 2009, 135(9): 600-610. doi: 10.1061/(ASCE)TE.1943-5436.0000019
[10]	杨晓华, 万琪, 刘大鹏, 等. 新疆砾石土低路堤动力特性[J]. 交通运输工程学报, 2019, 19(3): 1-9. doi: 10.3969/j.issn.1671-1637.2019.03.001 YANG Xiao-hua, WAN Qi, LIU Da-peng, et al. Dynamic characteristics of gravel soil low embankment in Xinjiang[J]. Journal of Traffic and Transportation Engineering, 2019, 19(3): 1-9. (in Chinese) doi: 10.3969/j.issn.1671-1637.2019.03.001
[11]	BROWN S F, BRUNTON J M, STOCK A F. The analytical design of bituminous pavements[J]. Proceedings of the Institution of Civil Engineers, 1985, 79(1): 1-31. doi: 10.1680/iicep.1985.1077
[12]	BROWN S F. Soil mechanics in pavement engineering[J]. Géotechnique, 1996, 46(3): 383-426. doi: 10.1680/geot.1996.46.3.383
[13]	COLLINS I F, BOULBIBANE M. The application of shakedown theory to pavement design[J]. Metals and Materials, 1998, 4(4): 832-837. doi: 10.1007/BF03026408
[14]	SHARP R W, BOOKER J R. Shakedown of pavements under moving surface loads[J]. Journal of Transportation Engineering, 1984, 110(1): 1-14. doi: 10.1061/(ASCE)0733-947X(1984)110:1(1)
[15]	王娟, 余海岁. 道路安定理论的进展及其应用[J]. 岩土力学, 2014, 35(5): 1255-1262, 1268. doi: 10.16285/j.rsm.2014.05.026 WANG Juan, YU Hai-sui. Development and its application of shakedown theory for road pavements[J]. Rock and Soil Mechanics, 2014, 35(5): 1255-1262, 1268. (in Chinese) doi: 10.16285/j.rsm.2014.05.026
[16]	KRABBENHØFT K, LYAMIN A V, SLOAN S W. Shakedown of a cohesive-frictional half-space subjected to rolling and sliding contact[J]. International Journal of Solids and Structures, 2007, 44(11/12): 3998-4008.
[17]	NGUYEN A D, HACHEMI A, WEICHERT D. Application of the interior-point method to shakedown analysis of pavements[J]. International Journal for Numerical Methods in Engineering, 2008, 75(4): 414-439. doi: 10.1002/nme.2256
[18]	孙阳, 沈水龙, 罗春泳. 基于下限定理的路面结构安定分析[J]. 岩土力学, 2010, 31(11): 3667-3670. doi: 10.3969/j.issn.1000-7598.2010.11.051 SUN Yang, SHEN Shui-long, LUO Chun-yong. Shakedown analysis of pavement structures based on lower bound theorem[J]. Rock and Soil Mechanics, 2010, 31(11): 3667-3670. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.11.051
[19]	YU Hai-sui, WANG Juan. Three-dimensional shakedown solutions for cohesive-frictional materials under moving surface loads[J]. International Journal of Solids and Structures, 2012, 49(26): 3797-3807. doi: 10.1016/j.ijsolstr.2012.08.011
[20]	YU Hai-sui, HOSSAIN M Z. Lower bound shakedown analysis of layered pavements using discontinuous stress fields[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 167(3/4): 209-222.
[21]	SCHWARTZ C W, LI Rui, KIM S H, et al. Sensitivity evaluation of MEPDG performance prediction (2013)[R]. Washington DC: Transportation Research Board, 2011.
[22]	ZHOU Ren-yi, QIAN Jian-gu, HUANG Mao-song. Dynamic stress responses to traffic moving loading in the saturated poroelastic ground[C]//ASCE. Advances in Soil Dynamics and Foundation Engineering. Reston: ASCE, 2014: 117-125.
[23]	EASON G. The stresses produced in a semi-infinite solid by a moving surface force[J]. International Journal of Engineering Science, 1965, 2(6): 581-609. doi: 10.1016/0020-7225(65)90038-8
[24]	LYU Zhi, QIAN Jian-gu, SHI Zhen-hao, et al. Dynamic responses of layered poroelastic ground under moving traffic loads considering effects of pavement roughness[J]. Soil Dynamics and Earthquake Engineering, 2020, 130: 105996. doi: 10.1016/j.soildyn.2019.105996
[25]	BLEICH H. Uber die bemessung statisch unbestimmter stahltragwerke unter beruschsichtigung der elastisch- plastischen verhaltens des baustoffes[J]. Journal of Bauingenieur, 1932, 19: 261-269.
[26]	MELAN E. Der spannungsgudstand eines Henky-Mises schen kontinuums bei verlandicher belastung[J]. Sitzungberichte der Ak Wissenschaften Wie, 1938, 147(2): 73-87.
[27]	CHINH P D. An upper bound kinematic approach to the shakedown analysis of structures[J]. Meccanica, 1999, 34(1): 49-56. doi: 10.1023/A:1004427528433
[28]	AMBIRCO J M, BEGLEY M R. Plasticity in fretting contact[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(11): 2391-2417. doi: 10.1016/S0022-5096(99)00103-9
[29]	KÖNIG J A, MAIER G. Shakedown analysis of elastoplastic structures: a review of recent developments[J]. Nuclear Engineering and Design, 1981, 66(1): 81-95. doi: 10.1016/0029-5493(81)90183-7
[30]	PONTER A R S, KARADENIZ S. An extended shakedown theory for structures that suffer cyclic thermal loading, Part 1: theory[J]. Journal of Applied Mechanics, 1985, 52(4): 877-882. doi: 10.1115/1.3169162
[31]	PRAGER W. Bauschinger adaptation of rigid, workhardening trusses[J]. Mechanics Research Communications, 1974, 1(5/6): 253-256.
[32]	LEVINE H S, ARMEN H, WINTER R, et al. Nonlinear behavior of shells of revolution under cyclic loading[J]. Computers and Structures, 1973, 3(3): 589-617. doi: 10.1016/0045-7949(73)90099-0
[33]	CERADINI G. Dynamic shakedown in elastic-plastic bodies[J]. Journal of the Engineering Mechanics Division, 1980, 106(3): 481-499. doi: 10.1061/JMCEA3.0002600
[34]	ROWE P W. Displacement and failure modes of model offshore gravity platforms founded on clay[C]//Spearhead. Proceedings of the Offshore Europe Conference. Aberdeen: Spearhead, 1975: 1-7.
[35]	RAAD L, WEICHERT D, NAJM W. Stability of multilayer systems under repeated loads[J]. Transportation Research Record, 1988(1207): 181-186.
[36]	RAAD L, WEICHERT D, HAIDAR A. Analysis of full-depth asphalt concrete pavements using shakedown theory[J]. Transportation Research Record, 1989(1227): 53-65.
[37]	RAAD L, WEICHERT D, HAIDAR A. Shakedown and fatigue of pavements with granular bases[J]. Transportation Research Record, 1989(1227): 159-172.
[38]	RAAD L, MINASSIAN G. The influence of granular base characteristics on upper bound shakedown of pavement structures[J]. Road Materials and Pavement Design, 2005, 6(1): 53-79. doi: 10.1080/14680629.2005.9689999
[39]	SHIAU S H, YU Hai-sui. Load and displacement prediction for shakedown analysis of layered pavements[J]. Transportation Research Record, 2000(1730): 117-124.
[40]	YU Hai-sui. Three-dimensional analytical solutions for shakedown of cohesive-frictional materials under moving surface loads[J]. Proceedings of the Royal Society A—Mathematical Physical and Engineering Sciences, 2005, 461(2059): 1951-1964. doi: 10.1098/rspa.2005.1445
[41]	王康宇, 庄妍, 张占荣, 等. 多个列车轮载作用下铁路道床结构安定性分析[J]. 中南大学学报(自然科学版), 2020, 51(8): 2343-2352. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202008028.htm WANG Kang-yu, ZHUANG Yan, ZHANG Zhan-rong, et al. Shakedown analysis of railway ballast structure under multiple wheel loads[J]. Journal of Central South University (Science and Technology), 2020, 51(8): 2343-2352. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202008028.htm
[42]	ZHUANG Yan, WANG Kang-yu. Shakedown solutions for pavement structures with Von Mises criterion subjected to Hertz loads[J]. Road Materials and Pavement Design, 2018, 19(3): 710-726. doi: 10.1080/14680629.2017.1301265
[43]	庄妍, 王孟, 王康宇. 移动荷载作用下结构弹塑性安定分析方法及其应用研究[J]. 湖南大学学报(自然科学版), 2018, 45(7): 93-102. doi: 10.16339/j.cnki.hdxbzkb.2018.07.012 ZHUANG Yan, WANG Meng, WANG Kang-yu. Study on shakedown analysis method of elastic-plastic structures under moving loads structures and its application[J]. Journal of Hunan University (Natural Sciences), 2018, 45(7): 93-102. (in Chinese) doi: 10.16339/j.cnki.hdxbzkb.2018.07.012
[44]	庄妍, 王康宇, 董晓强, 等. 基于荷载包络图的铁路道床-路基结构安定性分析[J]. 太原理工大学学报, 2020, 51(5): 731-736. doi: 10.16355/j.cnki.issn1007-9432tyut.2020.05.016 ZHUANG Yan, WANG Kang-yu, DONG Xiao-qiang, et al. Shakedown analysis of ballasted track structure based on load envelope diagram[J]. Journal of Taiyuan University of Technology, 2020, 51(5): 731-736. (in Chinese) doi: 10.16355/j.cnki.issn1007-9432tyut.2020.05.016
[45]	宋修广, 张营超, 庄培芝, 等. 基于遗传算法的道路安定极限优化求解方法[J]. 山东大学学报(工学版), 2021, 51(5): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-SDGY202105001.htm SONG Xiu-guang, ZHANG Ying-chao, ZHUANG Pei-zhi, et al. Optimal calculation method of pavement shakedown limit based on genetic algorithm[J]. Journal of Shandong University (Engineering Science), 2021, 51(5): 1-7. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDGY202105001.htm
[46]	PONTER A R S, HEARLE A D, JOHNSON K L. Application of the kinematical shakedown theorem to rolling and sliding point contacts[J]. Journal of the Mechanics and Physics of Solids, 1985, 33(4): 339-362. doi: 10.1016/0022-5096(85)90033-X
[47]	COLLINS I F, CLIFFE P F. Shakedown in frictional materials under moving surface loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(4): 409-420. doi: 10.1002/nag.1610110408
[48]	COLLINS I F, WANG A P, SAUNDERS L R. Shakedown in layered pavements under moving surface loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(3): 165-174. doi: 10.1002/nag.1610170303
[49]	COLLINS I F, BOULBIBANE M. Geomechanical analysis of unbound pavements based on shakedown theory[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126: 50-59. doi: 10.1061/(ASCE)1090-0241(2000)126:1(50)
[50]	PONTER A R S, ENGELHARDT M. Shakedown limits for a general yield condition: implementation and application for a Von Mises yield condition[J]. European Journal of Mechanics—A/Solids, 2000, 19(3): 423-445. doi: 10.1016/S0997-7538(00)00171-6
[51]	BOULBIBANE M, COLLINS I F, PONTER A R S, et al. Shakedown of unbound pavements[J]. Road Materials and Pavement Design, 2005, 6(1): 81-96. doi: 10.1080/14680629.2005.9690000
[52]	CHEN Hao-feng, PONTER A R S. The linear matching method for shakedown and limit analyses applied to rolling and sliding point contact problems[J]. Road Materials and Pavement Design, 2005, 6(1): 9-30. doi: 10.1080/14680629.2005.9689997
[53]	QIAN Jian-gu, WANG Yong-gang, LIN Zhi-guo, et al. Dynamic shakedown analysis of flexible pavement under traffic moving loading[J]. Procedia Engineering, 2016, 143: 1293-1300. doi: 10.1016/j.proeng.2016.06.140
[54]	QIAN Jian-gu, LIN Han, GU Xiao-qiang, et al. Dynamic shakedown limits for flexible pavement with cross-anisotropic materials[J]. Road Materials and Pavement Design, 2020, 21(2): 310-330.
[55]	王永刚, 钱建固. 移动荷载下三维半空间动力安定性下限分析[J]. 岩土力学, 2016, 37(增1): 570-576. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1074.htm WANG Yong-gang, QIAN Jian-gu. Dynamic shakedown lower-bound analysis of three-dimensional half-space under moving load[J]. Rock and Soil Mechanics, 2016, 37(S1): 570-576. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1074.htm
[56]	QIAN Jian-gu, WANG Yong-gang, WANG Juan, et al. The influence of traffic moving speed on shakedown limits of flexible pavements[J]. International Journal of Pavement Engineering, 2019, 20(2): 233-244.
[57]	QIAN Jian-gu, DAI Yu-chen, HUANG Mao-song. Dynamic shakedown analysis of two-layered pavement under rolling-sliding contact[J]. Soil Dynamics and Earthquake Engineering, 2020, 129: 105958.
[58]	DAI Yu-chen, QIAN Jian-gu, WANG Yong-gang, et al. Dynamic shakedown analysis of flexible pavements under rolling and sliding contact considering moving speed[J]. Procedia Engineering, 2017, 189: 283-290.
[59]	WANG Juan, LIU Shu, YANG Wen-bo. Dynamics shakedown analysis of slab track substructures with reference to critical speed[J]. Soil Dynamics and Earthquake Engineering, 2018, 106: 1-13.
[60]	LIU Shu, WANG Juan. Application of shakedown theory in track substructure design[J]. Proceedings of the Institution of Civil Engineers—Ground Improvement, 2019, 172(2): 116-123.
[61]	WANG Juan, LIU Shu, TANG Xiao-jun. Theoretical solutions for static and dynamic shakedown of cohesive-frictional materials under moving loads[C]//Springer. 7th International Symposium on Environmental Vibration and Transportation Geodynamics (ISEV). Berlin: Springer, 2016: 269-279.
[62]	LIN Han, QIAN Jian-gu, WANG Yong-gang. Dynamic shakedown analysis for anisotropic material under traffic moving loading[M]//Springer. Environmental Vibrations and Transportation Geodynamics. Berlin: Springer. 2018: 159-166.
[63]	JOHNSON K L. Contact mechanics[J]. Journal of Tribology, 1986, 108(4): 659.
[64]	CONNOLLY D N, GIANNOPOULOS A, FORDE M C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments[J]. Soil Dynamics and Earthquake Engineering, 2013, 46: 13-19.
[65]	KOUROUSSIS G, VERLINDEN O, CONTI C. Finite-dynamic model for infinite media: corrected solution of viscous boundary efficiency[J]. Journal of Engineering Mechanics, 2011, 137(7): 509-511.
[66]	WANG Juan, YU Hai-sui. Shakedown analysis for design of flexible pavements under moving loads[J]. Road Materials and Pavement Design, 2013, 14(3): 703-722.
[67]	YU Hai-sui, WANG Juan, LIU Shu. Three-dimensional shakedown solutions for cross-anisotropic cohesive-frictional materials under moving surface loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(4): 331-348.
[68]	谭忆秋, 肖神清, 熊学堂. 路面抗滑性能检测与预估方法综述[J]. 交通运输工程学报, 2021, 21(4): 32-47. doi: 10.19818/j.cnki.1671-1637.2021.04.002 TAN Yi-qiu, XIAO Shen-qing, XIONG Xue-tang. Review on detection and prediction methods for pavement skid resistance[J]. Journal of Traffic and Transportation Engineering, 2021, 21(4): 32-47. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2021.04.002
[69]	马建, 赵祥模, 贺拴海, 等. 路面检测技术综述[J]. 交通运输工程学报, 2017, 17(5): 121-137. http://transport.chd.edu.cn/article/id/201705012 MA Jian, ZHAO Xiang-mo, HE Shuan-hai, et al. Review of pavement detection technology[J]. Journal of Traffic and Transportation Engineering, 2017, 17(5): 121-137. (in Chinese) http://transport.chd.edu.cn/article/id/201705012
[70]	ZHAO Ji-dong, SLOAN S W, LYAMIN A V, et al. Bounds for shakedown of cohesive-frictional materials under moving surface loads[J]. International Journal of Solids and Structures, 2008, 45(11/12): 3290-3312.
[71]	ZHUANG Yan, WANG Kang-yu. Three-dimensional shakedown analysis of ballasted railway structures under moving surface loads with different load distributions[J]. Soil Dynamics and Earthquake Engineering, 2017, 100: 296-300.