Adaptive Triangular Mesh Generation of Ship Hull Surface Based on NURBS
Article Text (Baidu Translation)
-
摘要: 针对面向曲面的三维船体性能计算和真实感图形显示问题, 应用NURBS曲线、曲面理论, 提出一种新颖的船体NURBS曲面三角形网格自动生成算法, 运用四角编码方法和改进的曲面片平坦性检验方法, 保证在递归分割船体NURBS曲面时, 能够快速有效地分割出四边形网格, 在曲面片的高度方向和边界处同时满足给定的精度要求, 在此基础上, 应用割角剖分算法将一个四边形网格剖分成两个或多个三角形网格。应用结果表明, 应用该算法生成的三角形平面片能够较好地逼近船体曲面, 避免出现网格间的裂缝, 与二叉树、四叉树方法相比, 四角编码方法明显节省了时间和空间, 提高了算法效率。Abstract: Aimed at the calculation of 3-D ship hull property and display of real image, an innovative arithmetic for adaptive triangular mesh generation of ship hull surface based on NURBS was put forward by NURBS curve and surface theories, combining quadrangle coding method and improved surface evenness checking method were proposed, which were capable of subdividing quadrangle grids quickly and effectively when the NURBS surface of ship hull was recursively subdivided for satisfying the gave precision requirements in the height direction and on the boundary of the surface, a quadrangle grid was divided into two or more triangle grids by cut corner arithmetic.Applied result indicates that the triangle hull surface created by the arithmetic approximates real ship hull, none of cracks appears among grids, the quadrangle coding method distinctly saves time and space compared with binary-tree method and quard-tree method, improves the efficiency of the arithmetic.
-
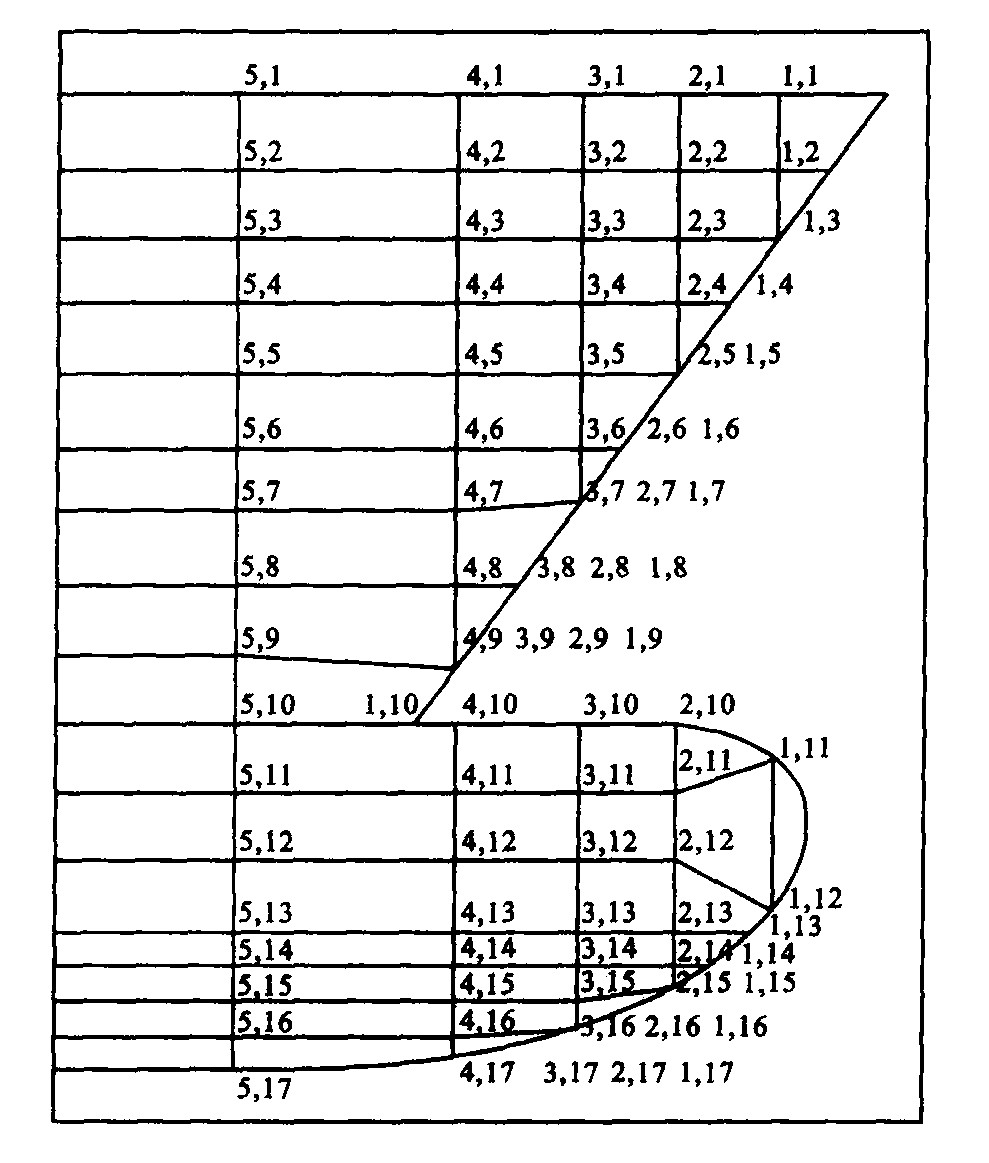
表 1 编码结果
Table 1. Coding Result
umin umax vmin vmax 曲面片1 1 3 2 4 曲面片2 7 8 1 4 -
[1] SCHWEITZER D, COBB E S. Scanline Rendering of Parametric Surfaces[J]. Computer Graphics, 1982, 16 (3): 265-274. doi: 10.1145/965145.801289 [2] FILIP D, GOLDMAN R. Conversion from Bezier Rectangles to Bezier Triangles[J]. Computer Aided Design, 1987, 19 (1): 25-28. doi: 10.1016/0010-4485(87)90149-7 [3] FILIP D, MAGEDSON R, MARKOT R. Surface Algorithms Using Bounds on Derivatives[J]. Computer Aided Geometric Design, 1987, 3 (4): 295-311. [4] 周建亮, 唐荣锡. NURBS曲面的自适应离散[J]. 工程图学学报, 1994, 15 (2): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-GCTX402.000.htmZHOU Jian-liang, TANG Rong-xi. Adaptive Subdivision of NURBS Surface[J]. Journal of Engineering Graphics, 1994, 15 (2): 1-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCTX402.000.htm [5] 章仁江, 王国瑾. 参数曲面用插值三角平面片逼近的误差估计[J]. 计算数学, 2004, 26 (2): 170-178. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSX200402004.htmZHANG Ren-jiang, WANG Guo-jin. The Error Estimates for Approximating Paramtric Surface by Interpolated Plane Triangular Patch[J]. Mathematica Numerica Sinica, 2004, 26 (2): 170-178. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSX200402004.htm [6] PIEGL L, TILLER W. The NURBS Book[M]. Berlin: Springer, 1997. [7] DEBOOR C. On Calculating with B-Splines[J]. Journal Approxi mation Theory, 1972, 6 (1): 50-62. doi: 10.1016/0021-9045(72)90080-9 [8] FARI N G. Curves and Surfaces for Computer Aided Geometric Design[M]. San Diego: Academic Press, 1996. [9] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 北京航空航天大学出版社, 1994. [10] SHENG X, HIRSHB E. Triangulation of Trimmed Surfacein Parametric Space[J]. CAD, 1992, 24 (8): 437-444. [11] VIGO M, PLAN, BRUNETP. Directional Adaptive Surface Triangulation[J]. Computer Aided Geometric Design, 1999, 16 (2): 107-126. doi: 10.1016/S0167-8396(98)00040-5 [12] COHEN E, LYCHE T, RIESENFELD R. Discrete B-Splinesand Subdivision Techniques in Computer aided Geometric Design and Computer Graphics[J]. Computer Graphics and Image Process, 1980, 14 (2): 87-111. doi: 10.1016/0146-664X(80)90040-4 [13] VIGO M. An Improved Incremental Algorithmfor Constructing Restricted Delaunay Triangulations[J]. Computer and Graphics, 1997, 21 (2): 215-233. doi: 10.1016/S0097-8493(96)00085-4 [14] PIEGL L, ARNAUD M. Algorithm and Data Structure for Triangulating Multiply Connected Polygonal Domains[J]. Computer and Graphics, 1993, 17 (5): 563-574. doi: 10.1016/0097-8493(93)90007-V [15] HERZEN V B, BARRALAN H. Accurate Triangulations of Deformed Intersecting Surfaces[J]. Computer and Graphics, 1987, 21 (4): 103-110. doi: 10.1145/37402.37415 [16] NAKAJI MA N, TOKMASU S, KUNITOMO Y. Feather-Based Heuristics for Finite-Element Meshing Using Quadtress and Octrees[J]. CAD, 1992, 24 (12): 667-690. [17] SNYDER J, BARRALAN H. Ray Tracing Complex Models Containing Surface Tessellations[A]//Proeedings of 14th Annual Conference on Computer Graphics and Interactive Techniques[C]. New York: ACMPress, 1987. -





 下载:
下载: