Mechanical behavior of prestressed concrete T beam based on mixed shell element method
-
摘要: 为了准确预测与评估预应力混凝土T梁的力学性能, 利用混合壳单元建立了T梁有限元计算模型, 对T梁从完好状态至破坏状态的力学行为进行了非线性分析。T梁中弯曲预应力钢筋采用组合壳单元模型, 应用虚功原理推导了其对组合壳单元刚度矩阵的贡献, 梁底平直预应力钢筋采用分层壳单元模型; 利用Owen双参数屈服准则和Hinton压碎准则描述混凝土材料非线性特性, 采用双折线本构模型模拟钢筋材料。分析结果表明: 混合壳单元法计算结果与试验结果吻合良好, 弹性阶段的T梁刚度折减不明显, 非线性阶段刚度发生明显折减, 跨中预应力钢筋应力增长幅度最大, 因此, 混合壳单元法对预应力混凝土T梁力学行为分析是有效的。Abstract: In order to accurately forecast and estimate the mechanical property of prestressed concrete T beam, its finite element model was set up by using mixed shell elements, and the nonlinear process of its mechanical behavior from wholeness to failure was studied. In T beam, curving prestressed steel was simulated with combined shell element model, its contribution to the stiffness matrix of combined shell element was deduced by using virtual principle, and straight prestressed steel was simulated with layered shell element model; the material nonlinear behavior of concrete was considered with Owen yield criterion and Hinton crushing criterion, and the behavior of steel was depicted with bilinear constitutive model. Analysis result indicates that the computational result of the model is close to experimental result, the stiffness degradation coefficient of T beam in nonlinearity phase is much larger than that in elasticity phase, and the most increase of steel stress is at the bottom of mid-span, so mixed shell element method is efficient and proper to analyze the mechanical behavior of prestressed concrete T beam.
-
图 2 平直预应力钢筋的分层壳元模型
Figure 2. Layered shell element model of straight prestressed steel
图 3 弯曲预应力钢筋的组合壳元模型
Figure 3. Combined shell element model of curving prestressed steel
图 4 预应力混凝土T梁的构造及加载方式
Figure 4. Configuration of prestessed concrete T beam and positions of added loads
表 1 跨中的刚度折减
Table 1. Stiffness degradation in middle span
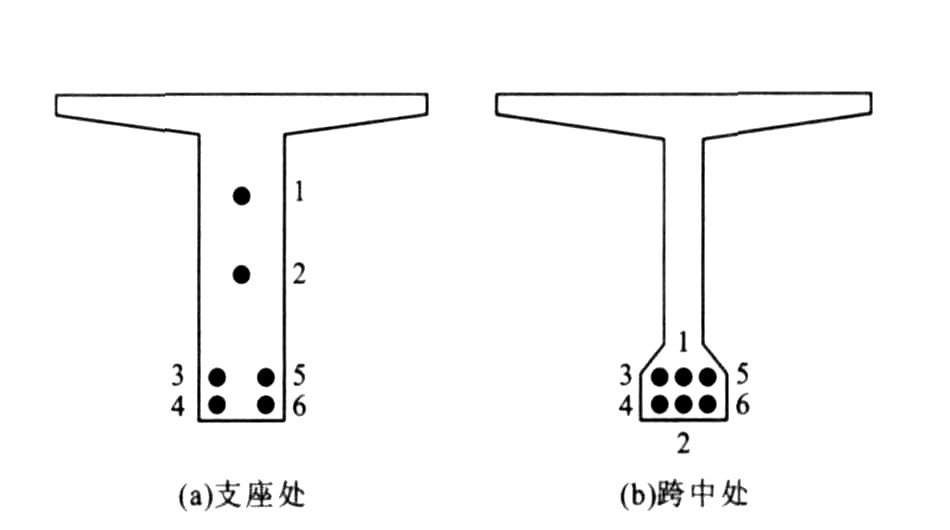
荷载步 荷载/kN 跨中挠度/mm 荷载比跨中挠度/(kN·mm-1) 刚度折减程度/% 注 1 0.00 0.00 弹性阶段 2 80.00 6.00 13.32 100.00 11 630.60 48.26 13.07 98.07 14 765.60 61.41 12.47 93.58 15 810.80 67.52 12.01 90.14 非线性阶段 17 900.80 86.48 10.42 78.18 20 1 035.80 199.11 5.20 39.05 22 1 130.00 551.65 2.05 15.38 
下载: 导出CSV
表 2 跨中预应力钢筋的应力重分布
Table 2. Redistribution of stress in middle span
荷载步 荷载/kN 应力/MPa 荷载增量/kN 应力增量/MPa 应力增长率/(MPa·kN-1) 重分布系数 注 1 0.00 1 050.00 弹性阶段 2 80.00 1 076.96 80.00 26.96 0.34 1.00 11 630.60 1 310.38 45.00 33.89 0.75 2.23 14 765.60 1 451.43 45.00 22.71 0.50 1.50 15 810.80 1 471.05 45.20 19.62 0.43 1.29 非线性阶段 17 900.80 1 508.84 45.20 27.10 0.60 1.78 20 1 035.80 1 543.97 45.00 6.73 0.15 0.44 22 1 130.00 1 597.02 49.20 34.67 0.70 2.09
下载: 导出CSV
-
[1] 陈水生, 万益春, 野田尚昭. 隔震桥梁地震响应非线性分析[J]. 长安大学学报: 自然科学版, 2006, 26(1): 54-58. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200601011.htmChen Shui-sheng, Wan Yi-chun, Nao-aki Noda. Nonlinear response of isolated-bridge subjected to seismic excitation[J]. Journal of Chang an University: Natural Science Edition, 2006, 26(1): 54-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200601011.htm [2] 王钧利, 贺拴海. 高墩大跨径弯桥在悬臂施工阶段刚构的非线性稳定分析[J]. 交通运输工程学报, 2006, 6(2): 30-34. http://transport.chd.edu.cn/article/id/200602007Wang Jun-li, He Shuan-hai. Nonlinear stability analysis of long-span curve bridge with high piers during cantilever construction[J]. Journal of Traffic and Transportation Engineering, 2006, 6(2): 30-34. (in Chinese) http://transport.chd.edu.cn/article/id/200602007 [3] 杨耀铨. 跨径25 m的装配式后张法预应力混凝土简支梁静载试验小结[R]. 武汉: 交通部第二公路勘察设计院, 1979. [4] Song H W, You D W, Byun KJ, et al. Finite element failure analysis of reinforced concrete T-girder bridges[J]. Engineering Structures, 2002, 24(2): 151-162. doi: 10.1016/S0141-0296(01)00107-9 [5] 吕西林, 金国芳, 吴晓涵. 钢筋混凝土结构非线性有限元理论与应用[M]. 上海: 同济大学出版社, 1999. [6] 康清梁. 钢筋混凝土有限元分析[M]. 北京: 中国水利水电出版社, 1996. [7] Fragiacomo M, Amadio C, Macorini L. Finite-element model for collapse andlong-termanalysis of steel-concrete composite beams[J]. Journal of Structural Engineering, 2004, 130(3): 489-497. doi: 10.1061/(ASCE)0733-9445(2004)130:3(489) [8] Deng Lin-zhong, Michel G, Ales Z, et al. Nonlinear flexural behavior of prestressed concrete girder bridges[J]. Journal of Bridge Engineering, 2001, 6(4): 276-284. doi: 10.1061/(ASCE)1084-0702(2001)6:4(276) [9] Wendel MS, Richard E M. Nonlinear F Eanalysis of steelconcrete composite structures[J]. Journal of Structural Engineering, 2000, 126(6): 662-674. doi: 10.1061/(ASCE)0733-9445(2000)126:6(662) [10] Wonseok C, Elisa DS. Nonlinear finite-element analysis of composite steel girder bridges[J]. Journal of Structural Engi-neering, 2005, 131(2): 304-313. doi: 10.1061/(ASCE)0733-9445(2005)131:2(304) [11] 刘小燕, 颜东煌, 张峰, 等. 预应力高强混凝土梁极限承载力分析[J]. 中国公路学报, 2006, 19(1): 58-61. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601011.htmLiu Xiao-yan, Yan Dong-huang, Zhang Feng, et al. Ultimate load analysis of prestressed high-strength concrete beam[J]. China Journal of Highway and Transport, 2006, 19(1): 58-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601011.htm [12] 王勖成, 邵敏. 有限单元法基本原理和数值方法[M]. 北京: 清华大学出版社, 1995. [13] 王家林. 钢筋混凝土结构空间有限元分析的体梁组合单元[J]. 工程力学, 2002, 19(6): 131-135. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200206025.htmWang Jia-lin. Abrick-beamcombination element for three-dimensional finite element analysis of reinforced concrete structures[J]. Engineering Mechanics, 2002, 19(6): 131-135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200206025.htm -
点击查看大图
图(7) / 表(2)
计量
- 文章访问数: 279
- HTML全文浏览量: 92
- PDF下载量: 311
- 被引次数: 0
