0.   引言

随着国际贸易的增加和集装箱运输技术的改进, 货物运输的集装箱化率日益提高, 集装箱运输市场获得了快速发展。在枢纽港之间, 大型集装箱船舶形成了干线运输方式; 在喂给港到枢纽港之间, 则是以中小型船舶为主的支线运输构成了轴-辐式的海上运输模式。从航运企业层面看, 航线优化、船舶调度是影响船队运营效益与企业竞争能力的关键因素, 因此, 合理设计集装箱船舶航线、节省运输时间和成本具有积极的意义。

目前国内外有关航线设计、船舶调度的研究主要集中于干散货船、油轮和集装箱班轮等干线运输方面, Christiansen等将车辆路线问题(VRP) 扩展到散货船运输, 并提出了集送一体化的软时间窗与多型船舶的调度模型^[1-2]; Bronmo等设计了带有多初始点的局域搜索启发式算法, 并对船舶调度问题进行了求解, 结果表明此算法在合理时间内能够收敛到最优解或最优解领域, 与局域搜索算法相比, 在计算时间和解的质量2个方面具有一定的优越性^[3]; Pang等在考虑泊位利用率的基础上, 研究了如何设计船舶航线才能够减小泊位的拥堵问题, 建立了优化模型, 并采用启发式算法进行求解, 结果表明模型算法是有效的^[4]; Kosmas等从运营成本的角度考虑航线优化问题, 利用模拟退火算法对问题进行了求解, 采用方差分析对求解结果进行了讨论, 并把研究散货和油轮运输的理论与方法进一步应用到集装箱港口作业及航线规划的研究中^[5-7]; Meng等在考虑空箱存储的基础上, 研究了集装箱班轮运输网络设计问题, 建立了混合整数规划问题, 将此模型应用到亚欧集装箱运输网络中, 并验证了模型的合理性^[8]; Gelareh等针对竞争环境下的班轮网络设计问题建立了混合整数规划模型, 并用改进的拉格朗日松弛算法对模型进行了求解, 结果表明该方法具有较强的实用性^[9]; Hsu等以营运成本和库存成本为最小目标函数, 建立了描述轴-辐式集装箱运输网络的双目标模型, 求解出最佳的船舶航线及每条航线上的船型和发船频率, 解决了直达运输或选择转运港运输的轴-辐航线网络设计问题^[10]; Karlaftis等研究了在枢纽港和众多喂给港之间的集装箱船舶航线设计问题时, 建立了整数规划模型, 但没有考虑船舶在港的作业时间和等泊时间^[11]; 靳志宏等针对支线轴-辐式海上运输模式, 以成本最低为目标函数, 考虑了时间窗约束, 构建调度模型, 并运用粒子群算法进行求解, 模型仅考虑支线运营的航行成本和箱位利用率, 没有考虑船舶的航线规划问题^[12-13]。

目前, 有关支线船舶航线设计及优化调度问题的研究成果较少。本文针对支线运输中喂给港数目众多, 港口货源数量少以及没有固定的航线等问题, 考虑船舶容量及运营时间限制等因素, 建立混合整数规划模型, 并设计相应的算法求解, 求得航线数及每条航线依次挂靠的港口。

1.   数学模型

1.1   问题描述

支线集装箱运输包括沿海支线集装箱运输和内河支线集装箱运输。沿海支线运输是指国内沿海港口之间的内支线运输; 内河支线运输是指内河港口至内河港口或至沿海港口之间的内支线运输。本文主要研究枢纽港和众多喂给港之间的集装箱运输问题, 即轴-幅式运输模式, 见图 1。需要通过支线运输送到各喂给港的集装箱统一在枢纽港卸下, 由中小型集装箱船输送到各喂给港, 并且将每个喂给港需要进行干线运输的集装箱运回到枢纽港。这不同于经典的VRP, 而是由多个VRP构成的组合优化问题。船舶在每个喂给港要卸掉枢纽港到喂给港的集装箱, 装载喂给港到枢纽港的集装箱, 还要满足船舶装载容量限制, 船舶运营过程中要考虑送往枢纽港的集装箱赶大船的时间限制, 是一个带有时间窗约束和容量约束的NP-hard优化问题。

图  1  轴-辐式运输模式

Figure  1.  Hub-and-spoke transportation mode

下载: 全尺寸图片 幻灯片

1.2   模型假设

(1) 根据船舶的作业功能, 假设船舶总是从枢纽港装箱出发, 最后再驶回枢纽港, 不考虑各喂给港之间的集装箱运输任务。

(2) 在目标函数中, 从船舶驶离枢纽港开始计算总航行时间, 当船舶驶回枢纽港时截止计时; 各喂给港的作业时间由港口装卸箱总数量和码头岸桥设备作业效率确定。

(3) 考虑到各喂给港的集装箱运到枢纽港是为了通过干线集装箱班轮运往其他枢纽港, 故每个喂给港的集装箱运达枢纽港有一定的时间限制, 以确保赶上班轮班期。

1.3   模型建立

在模型中, 设定C为船队需要服务的所有喂给港口的数量; V为船队船舶数量; t_kij为船舶k从喂给港i航行到喂给港j所需要的时间; s_ki为船舶k在喂给港i的作业时间; w_ki为船舶k在喂给港i的等待靠泊时间; t_ki为船舶k到达喂给港i的时间点; p_i为从枢纽港到喂给港i的卸箱量; q_i为从喂给港i需要运到枢纽港的总箱量; L_k为船舶k的最大载运量; N_i为规定喂给港i的货物送达枢纽港的限制时间; n_kr为船舶k航行在r航线时, 该航线所包含的港口数量; 决策变量为

$x{}_{kij}=\{\begin{array}{cc}1\hfill & \text{船}\text{舶}k\text{从}\text{喂}\text{给}\text{港}i\text{驶}\text{到}\text{喂}\text{给}\text{港}j\hfill \\ 0\hfill & \text{其}\text{他}\hfill \end{array}$

完成所有港口的集装箱运输任务所花费的最小时间目标函数(总航行时间) T为

$\begin{array}{l}\min {\rm T}={\displaystyle \sum _{i=1}^C{\displaystyle \sum _{j=1}^C{\displaystyle \sum _{k=1}^{V}t}}}{}_{kij}x{}_{kij}+{\displaystyle \sum _{i=2}^C{\displaystyle \sum _{k=1}^{V}s}}{}_{ki}+{\displaystyle \sum _{i=2}^C{\displaystyle \sum _{k=1}^{V}w}}{}_{ki}\\ \text{s}.\text{t}.{\displaystyle \sum _{i=2}^{C}x}{}_{kij}\le 1j=2,\cdots ,C(1)\end{array}$

${\displaystyle \sum _{i=2}^C{\displaystyle \sum _{k=1}^{V}x}}{}_{kij}=1j=2,\cdots ,C(2)$

${\displaystyle \sum _{j=2}^{C}x}{}_{k1j}\le 1(3)$

${\displaystyle \sum _{i=2}^{C}x}{}_{ki1}\le 1(4)$

$\begin{array}{l}{\displaystyle \sum _{i=1}^{C}x}{}_{kid}-{\displaystyle \sum _{j=1}^{C}x}{}_{kdj}=0\\ d\ne i,d\ne j,d=2,\cdots ,C(5)\end{array}$

${\displaystyle \sum _{i=1}^C{\displaystyle \sum _{j=1}^{C}x}}{}_{kij}p{}_j\le L{}_k(6)$

$x{}_{kij}\left({\displaystyle \sum _{i=1}^{n{}_{kr}}{\displaystyle \sum _{j=1}^{n{}_{kr}}x}}{}_{kij}p{}_j-{\displaystyle \sum _{d=1}^{i}p}{}_d+{\displaystyle \sum _{d=1}^{i}q}{}_d-p{}_j+q{}_j\right)\le L{}_k$

i, j=1, 2, …, n_kr; r=1, …, V (7)

$\begin{array}{l}x{}_{kij}\left(t{}_{ki}+s{}_{ki}+t{}_{kij}-t{}_{kj}\right)\le 0\\ i,j=1,2,\cdots ,C(8)\end{array}$

${\displaystyle \sum _{i=1}^{n{}_{kr}}{\displaystyle \sum _{j=1}^{n{}_{kr}}t}}{}_{kij}x{}_{kij}+{\displaystyle \sum _{i=1}^{n{}_{kr}}s}{}_{ki}+{\displaystyle \sum _{i=1}^{n{}_{kr}}w}{}_{ki}\le \min \left\{{\rm N}{}_i\right\}(9)$

目标函数由船舶航行时间、在港作业时间和在港等待时间3部分组成。约束式(1) 保证每艘船舶最多航行1条航线; 约束式(2) 保证每条航线只能由1艘船舶来航行; 约束式(3)、(4) 保证若船舶k航行1条航线, 则必须从枢纽港出发再回到枢纽港; 约束式(5) 保证当船舶驶入某喂给港就必须航出; 约束式(6) 保证从枢纽港出发时的载箱量不能超过船舶的最大载箱量; 约束式(7) 保证各喂给港装卸时的载箱量不能超过船舶的最大载运量; 约束式(8) 保证港口之间航行的连续性; 约束式(9) 保证每条航线的时间限制, 即每条航线的航行时间必须小于该航线上各喂给港规定的送至枢纽港的时间限制。

2.   算法设计

在求解上述模型时, 采用遗传算法思想, 改进解的结构并设计算法, 通过算法求解模型, 可以确定航线数量、每条航线依次所挂靠的港口与总航行时间的最优值。

2.1   遗传算法执行过程

遗传算法是借鉴生物界自然选择和自然遗传机制的随机化搜索算法, 借用了生物进化中“适者生存”的规律。对初始种群, 以适应度函数为依据, 通过选择、交叉和变异3种遗传算子对群体进行操作, 实现群体内个体结构重组, 以确定下1代较优的种群, 如此继续, 直到得到最优个体。遗传算法中包含4个基本要素: 解的结构、杂交算子、变异算子与选择算子^[14-15]。本文改进了遗传算法基本要素, 求解上述规划模型。

2.1.1   解的结构

在模型中, 假设有7个港口, 分别为枢纽港1和喂给港2、3、4、5、6、7, 则(1, 2, 3, 4, 5, 6, 7) 就代表 1个有实际意义的港口排列顺序, 并将其视为进行遗传操作的解。对于每个港口排列顺序, 都能找出符合航行约束条件的各条航线。

表  1  港口的作业量和时间

Table  1.  Working amouts and working times of ports

港口	卸箱量/TEU	装箱量/TEU	作业时间/h	限制时间/h		港口	卸箱量/TEU	装箱量/TEU	作业时间/h	限制时间/h
1南沙	0	0	0.0	0		16南伟	25	25	1.4	90
2盐田	20	25	1.2	80		17珠海	30	20	1.2	80
3惠州	21	27	0.8	80		18高栏	10	25	1.1	100
4新风	18	10	1.0	120		19斗门	20	16	1.0	110
5黄埔1	15	20	1.3	120		20阳江	25	21	1.0	200
6黄埔2	17	10	0.5	120		21水东	20	30	1.2	200
7增城	10	20	0.7	120		22海口	35	20	2.0	200
8太平	20	12	1.1	100		23湛江	20	28	1.0	200
9三山	15	25	1.2	110		24洋浦	10	20	0.9	200
10三水	15	22	1.0	140		25北海	20	21	1.4	200
11北滘	20	23	1.0	100		26防城	25	30	1.2	220
12容奇	15	9	1.0	100		27澳门	20	15	1.3	80
13江门	28	35	1.3	100		28蛇口	15	20	1.3	80
14中山	20	25	1.0	100		29新会	20	10	1.4	110
15三榕	15	20	1.3	140		30海防	15	22	1.2	220
注: 黄埔1和黄埔2分别为黄埔新港和黄埔旧港。

下载: 导出CSV 

| 显示表格

针对上述港口排列顺序, 从枢纽港1出发, 首先挂靠喂给港2, 然后判断当喂给港3加入到该航线后是否满足船舶容量和时间约束等条件, 若不满足则停止, 生成航线1—2—1, 下1条航线从挂靠喂给港3开始进行设计; 若满足, 则继续判断喂给港4加入该航线后是否满足约束条件, 不满足条件就停止, 生成航线1—2—3—1, 下1条航线从挂靠喂给港4开始设计; 当加入港口4后满足条件, 则继续向下依次判断, 直至所有喂给港都经过试探, 得出各条航线为止。

2.1.2   杂交算子

对编码后的解进行单点杂交, 在父代群体中采取双亲双子杂交规则, 对每组杂交的个体随机产生杂交点, 然后交换该点之后(包括该点) 的所有基因。考虑到解的编码和解码是遗传算法使用中的关键步骤, 在有众多喂给港的集装箱船舶航线设计问题中, 几乎不可能用二进制编码来表示解构成, 而简单的整数编码在遗传操作过程中也会产生无效解。如有2个父代个体进行杂交, 其父代个体分别为(1, 2, 3, 4, 5, 6, 7) 和(1, 3, 7, 5, 2, 6, 4), 杂交点选在位置4, 则产生的2个后代个体分别为(1, 2, 3, 4, 2, 6, 4) 和(1, 3, 7, 5, 5, 6, 7), 此时港口排列顺序中有重复的港口, 则产生了没有实际意义的排列顺序。为了保证任意的基因型个体都能够对应于每条具有实际意义的港口排列顺序, 本文采用巡回路线编码方法。

首先假设所有的港口最初按一定顺序排列为M= (1, 2, 3, 4, …, n), 并暂记为是对各港口挂靠的前后顺序, 在此基础上寻找满足船舶载运量和时间限制等条件的航行路线。规定每挂靠完1个港口, 就从上述排列顺序中将该港口的数字标号去掉, 则可用第i (i=1, 2, …, n) 个挂靠的港口在所有还没被挂靠的港口排列顺序中对应的位置序号g_i (1≤g_i≤n-i+1) 表示具体挂靠的港口。将全部g_i顺序排列在一起得到的列表G= (g₁, g₂, …, g_n) 就可以表示有实际意义的港口排列顺序, 即为遗传算法种群中的1个个体。

针对上述问题, 设港口原始排列顺序为M= (1, 2, 3, 4, 5, 6, 7) (1为枢纽港), 记为下排列顺序P₀为(1, 2, 3, 4, 5, 6, 7)。若船舶实际的挂靠顺序为(1, 4, 6, 5, 2, 7, 3), 即第1个挂靠的港口为枢纽港1, 枢纽港在P₀中的位置序号为1, 然后将该港口删除, 得排列顺序变为P₁为(2, 3, 4, 5, 6, 7)。第2个挂靠的港口为喂给港4, 其在P₁中的位置序号为3, 然后将该港口删除后得到排列顺序为P₂为(2, 3, 5, 6, 7)。第3个挂靠的港口为喂给港6, 其在P₂中的位置序号为4, 然后将该港口删除, 得到排列顺序为P₃为(2, 3, 5, 7)。如此继续, 直到处理完P₀中所有的港口, 最后得到各港口对应位置序号的排列顺序G为(1, 3, 4, 3, 1, 2, 1), 即为编码后的解。此时, 对编码后的解进行杂交操作就会产生有实际意义的后代个体

$\begin{array}{c}\text{父}\text{代}1:(1,2,3,4,5,6,7)\\ \text{父}\text{代}2:(1,3,7,5,2,6,4)\end{array}\stackrel{\text{编}\text{码}}{\to }\stackrel{\text{杂}\text{交}\text{点}}{{\displaystyle \begin{array}{c}(1,1,1,1,1,1,1)\\ (1,2,5,3,1,2,1)\end{array}}}\stackrel{\text{杂}\text{交}}{\to }$

$\begin{array}{c}(1,1,1,3,1,2,1)\\ (1,2,5,1,1,1,1)\end{array}\stackrel{\text{解}\text{码}}{\to }\begin{array}{c}\text{子}\text{代}1:(1,2,3,6,4,7,5)\\ \text{了}\text{代}2:(1,3,7,2,4,5,6)\end{array}$

相应地, 若有1个位置序号排列G为(1, 6, 4, 4, 3, 2, 1), 则可依据上述方法解码为港口挂靠顺序是(1, 7, 5, 6, 4, 3, 2)。

2.1.3   变异算子和选择算子

变异是以较小概率对个体编码串上的某个或某些位值进行改变。变异运算是指将个体染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换, 从而形成新的个体。在本文中, 变异概率取0.01。考虑到编码后的解只适合于杂交操作, 故变异操作是针对港口排列顺序采用换位变异法

随机选中的2个基因

↓ ↓

变异前$(1,2,3,4,5,6,7)\stackrel{}{\to }$变异后(1, 2, 7, 4, 5, 6, 3)

在本文模型中, 选择算子采用轮盘赌的方式获得下1代种群。

2.2   模型求解思路

步骤1  针对实际问题, 产生初始种群, 种群规模选取30。

步骤2  计算每个个体适应函数值, 即目标函数值, 保留最优值和最优解。

步骤3  判断是否满足遗传算法终止规则。本文选取迭代步数达到200时终止。若满足, 则输出最优结果; 若不满足, 则对群体进行遗传操作, 包括编码杂交, 解码变异, 轮盘赌选择, 并返回步骤2。

3.   案例分析

以某航运企业经营珠江三角洲区域的集装箱船舶支线运输任务为例, 内支线范围既有内河喂给港, 也有沿海喂给港。选取南沙港作为支线枢纽港, 另外有29个喂给港, 枢纽港的标号为1, 各喂给港分别按顺序标号为2~30。不考虑船舶在枢纽港的等泊时间, 可得各港口装(卸) 箱量、在港作业时间及各枢纽港船舶送达限制时间(作业量及时间) 见表 1。

结合实际情况, 本文分2种情况进行研究: 第1种只有1类船型, 船舶容量为200 TEU; 第2种有2类船型, 船舶容量分别为100、150 TEU。

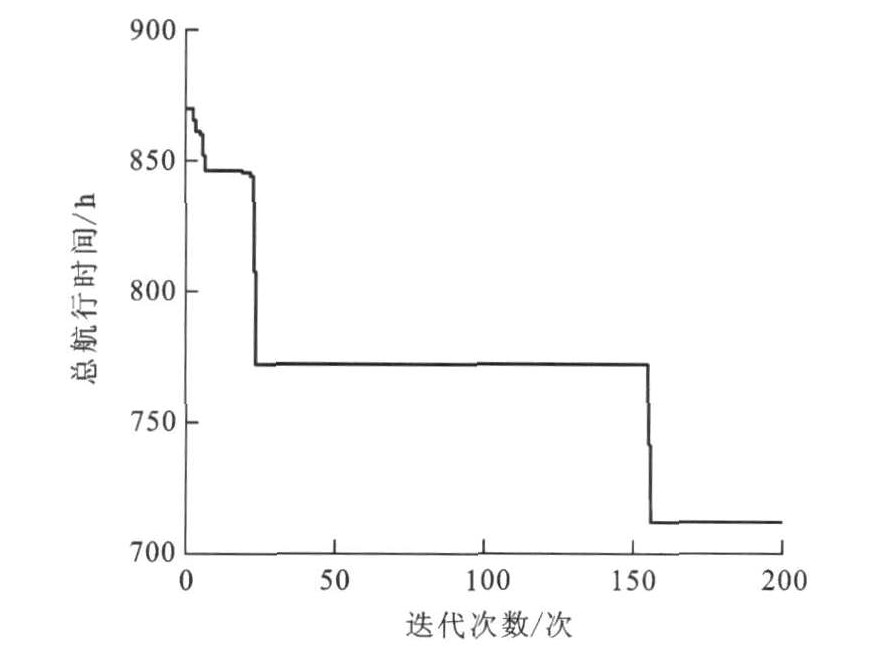
针对第1种情况, 应用改进的遗传算法求解, 航线优化结果见表 2。由表 2可以看出, 由于航行时间和船舶载质量的限制, 在单船型情况下, 可设计8条航线, 单船型航线设计见图 2。利用遗传算法求解时, 总航行时间随着遗传迭代次数的增大而逐渐收敛。当迭代次数达到160次以后, 此时的总航行时间为708.6 h, 见图 3。在单船型情况下, 共需要8艘200 TEU的集装箱船舶便可完成该支线运输任务。

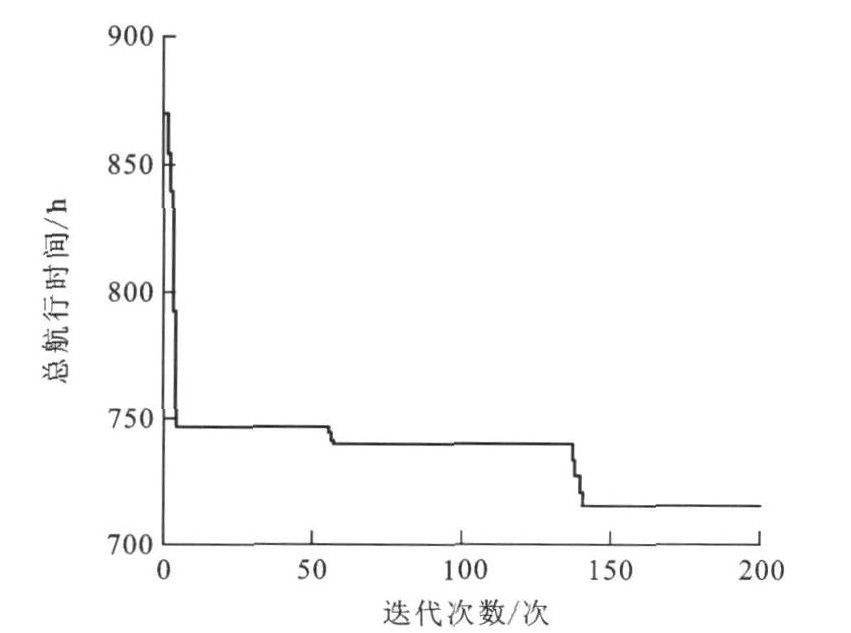
表  2  单船型情况下航线优化结果

Table  2.  Route optimization result under one type of ship

航线	挂靠喂给港口
1	南沙—三山—新风—黄埔2—黄埔1—增城—南沙
2	南沙—高栏—新会—江门—南沙
3	南沙—珠海—澳门—阳江—南沙
4	南沙—三榕—三水—南沙
5	南沙—洋浦—北海—防城—海防—海口—湛江—水东—南沙
6	南沙—北滘—容奇—太平—南沙
7	南沙—斗门—中山—南伟—南沙
8	南沙—盐田—惠州—蛇口—南沙

下载: 导出CSV 

| 显示表格

图  2  单船型航线设计

Figure  2.  Route designing under one type of ship

下载: 全尺寸图片 幻灯片

图  3  单船型下收敛结果

Figure  3.  Convergence result under one type of ship

下载: 全尺寸图片 幻灯片

针对第2种情况应用改进的遗传算法求解, 航线优化结果见表 3。在2种船型情况下, 设计出9条航线, 其中需要100 TEU船舶8艘, 150 TEU的船舶1艘。利用遗传算法求解的总航行时间收敛结果见图 4, 此时的总航行时间为714.6 h。

表  3  2种船型情况航线优化结果

Table  3.  Route optimization result under two types of ships

航线	挂靠喂给港口	容量/TEU
1	南沙—斗门—江门—容奇—南沙	100
2	南沙—水东—阳江—高栏—南沙	100
3	南沙—海口—洋浦—南沙	100
4	南沙—中山—珠海—澳门—南沙	100
5	南沙—三水—北滘—黄埔2—增城—太平—南伟—南沙	150
6	南沙—新风—黄埔1—南沙	100
7	南沙—三山—三榕—新会—南沙	100
8	南沙—蛇口—盐田—惠州—南沙	100
9	南沙—湛江—防城—北海—海防—南沙	150

下载: 导出CSV 

| 显示表格

图  4  两种船型下收敛结果

Figure  4.  Convergence result under two types of ships

下载: 全尺寸图片 幻灯片

通过以上分析可知, 使用同种船型和2种不同船型对总航行时间影响不大, 使用2种不同船型时可以充分利用船舶容量, 弥补单种船型时不能选择合适容量船舶的缺点, 避免造成船容量的浪费。

4.   敏感性分析

为进一步分析船型对运输效率的影响, 本文针对不同支线船舶容量和不同枢纽港船舶限制时间进行了敏感性分析。

4.1   方差分析

方差分析主要针对控制变量的不同水平是否对观测变量产生了显著影响, 本文只对支线船舶容量和枢纽港船舶限制时间统一变化进行方差分析。其中, 支线船舶容量分别取50、75、100、125、150、175、200、225、250 TEU; 枢纽港船舶限制时间(集装箱送达枢纽港的限制时间) 分为4种情况, 分别为T₁、T₂、T₃、T₄, 选取值分别为表 1限制时间的0.8、1.0、1.2、1.5倍。不同船舶容量和限制时间条件下的总航行时间见表 4; 对表 4数据进行方差分析, 结果见表 5。

表  4  不同约束条件下的总航行时间

Table  4.  Total navigation times under different constraints

船舶容量/TEU	限制时间/h
	T1	T2	T3	T4
50	1 053.6	974.6	982.6	977.6
75	883.6	851.6	847.6	831.6
100	812.6	821.6	786.6	778.6
125	779.6	784.6	752.1	750.6
150	757.6	749.6	743.6	748.6
175	758.6	743.6	741.6	727.6
200	749.6	738.6	734.6	722.6
225	751.6	723.6	721.6	704.6
250	753.6	723.6	714.6	704.6

下载: 导出CSV 

| 显示表格

表  5  方差分析结果

Table  5.  Variance analysis result h

差异源	平方和/h2	自由度	均方/h2	F统计量	概率	F临界值
受限制时间影响的因素	251 150.100	8	31 393.770	206.307	3.29×10-20	2.355 081
受船舶容量影响的因素	7 716.854	3	2 572.285	16.904	4.08×10-6	3.008 787
误差	3 652.083	24	152.170
总计	262 519.100	35

下载: 导出CSV 

| 显示表格

从表 5可以看出, 在显著水平α为0.05的情况下, 由于受限制时间和船舶容量的因素的F统计量值均大于临界值, 或者F检验统计量的概率值均小于显著性水平0.05, 所以认为不同船舶容量水平下总航行时间的均值存在显著差异, 船舶容量的不同对总航行时间产生了显著影响, 且限制时间的不同水平也对总航行时间产生了显著影响。

4.2   船舶容量敏感性分析

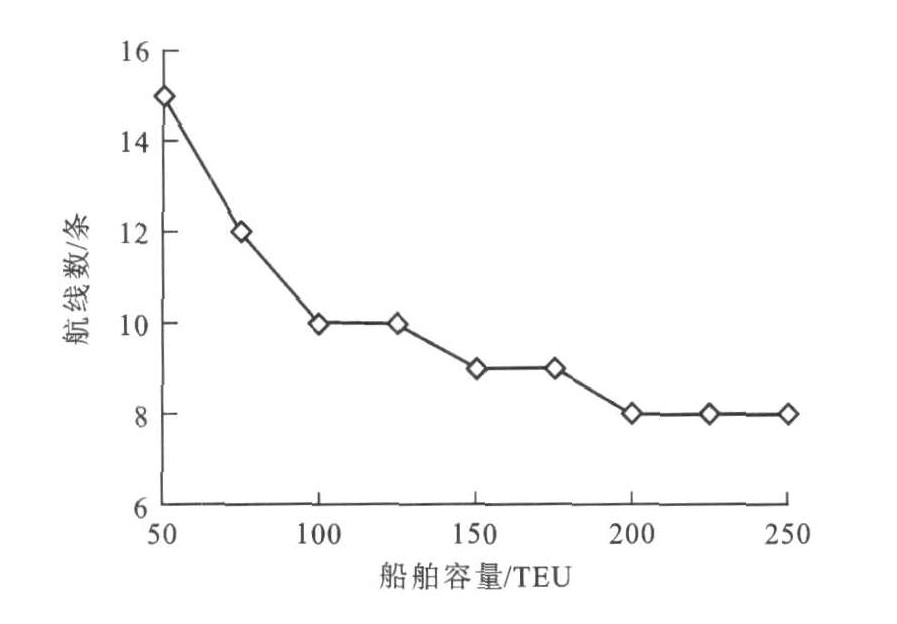
假设每艘船舶容量是固定的, 故当选择不同容量的船舶时, 设计的航线数与总航行时间都会发生变化。当选择不同容量的船舶时, 航线数量见图 5, 总航行时间见图 6。

图  5  航线数量

Figure  5.  Route number

下载: 全尺寸图片 幻灯片

图  6  总航行时间

Figure  6.  Total navigation time

下载: 全尺寸图片 幻灯片

由图 5可以看出, 当船舶容量从50 TEU增大到150 TEU时, 航线数量从15条下降到9条, 下降比较快; 但当船舶容量从150 TEU增大到250 TEU时, 航线数量变化不大, 仅减少1条, 趋于稳定; 再增大船舶容量时, 对航线数量影响不大。从图 6可以看出, 当船舶容量从50 TEU增大到150 TEU时, 总航行时间下降很快, 但当船舶容量从150 TEU增大到250 TEU时, 总航行时间相差不大。由以上分析可知, 当投入8艘容量为200 TEU的集装箱船舶, 就可完成该支线区域的集装箱运输任务。

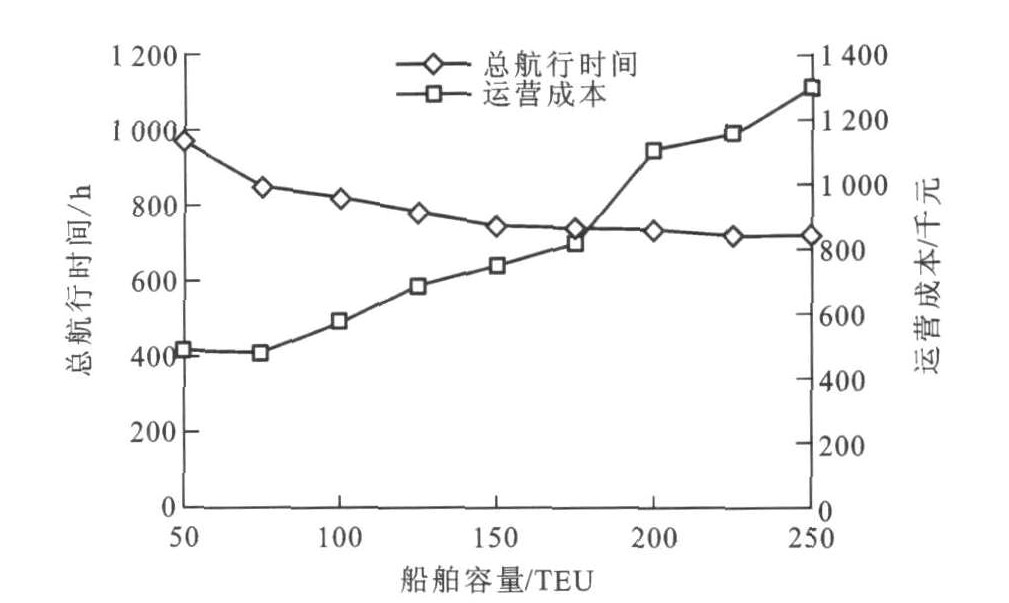
如果在设计航线时, 考虑总航行时间和船舶营运成本, 结果见图 7, 其中假设50 TEU的集装箱船舶每小时运营成本为0.5千元; 150 TEU的集装箱船舶每小时运营成本为1.0千元; 250 TEU的集装箱船舶每小时运营成本为1.8千元; 其他船型的运营成本介于上述3者之间。在此种情况下, 选择9艘容量为175 TEU的集装箱船舶即可完成该支线的运输任务, 运营成本也较低。

图  7  总航行时间和运营成本

Figure  7.  Total navigation times and running costs

下载: 全尺寸图片 幻灯片

4.3   限制时间敏感性分析

枢纽港船舶限制时间的变化也会对航线优化产生影响, 当船舶容量分别为100、150、200 TEU时, 枢纽港船舶限制时间对航线数量、总航行时间和运营成本的影响结果见表 6。从表 6可见, 虽然船舶容量变大时, 航线数量比较少, 但考虑大船的单船成本比较高, 故大船的运营成本远高于小船, 并且每艘船舶在不同限制时间下的运营成本变化幅度不大, 说明限制时间单独作用时对观测值影响较小, 因此, 可以根据实际情况选择在不同的限制时间下最合理的船型。当限制时间为T₁时, 100 TEU船舶的总航行时间明显高于其他2种船舶, 200 TEU船舶的运营成本又高于150 TEU船舶的, 故在航线条数相差不多的前提下, 应该选择150 TEU的船舶, 这也符合船舶容量敏感性分析的结果。

表  6  航线数量、总航行时间和运营成本

Table  6.  Route numbers, total navigation times and running costs

限制时间	船舶容量
	航线数量/条			总航行时间/h			运营成本/千元
	100 TEU	150 TEU	200 TEU	100 TEU	150 TEU	200 TEU	100 TEU	150 TEU	200 TEU
T1	11	10	10	812	758	748	510	730	1 060
T2	10	9	8	820	750	739	520	728	1 040
T3	10	9	7	786	743	734	504	728	1 030
T4	8	7	6	779	750	721	500	730	1 010

下载: 导出CSV 

| 显示表格

5.   结语

本文研究了集装箱船舶支线运输的航线设计问题, 针对班轮班期特点和船舶容量, 建立混合整数规划模型; 结合支线运输的特点, 设计了解结构, 提出了新的遗传算法, 并将此模型和算法应用到珠三角集装箱支线船舶运输问题中。数值分析结果表明该模型和算法可适用于实际情况下的集装箱船舶支线优化设计问题, 能够为支线运输企业提供辅助决策支持。