-
摘要: 利用经典的Dijkstra算法, 对重大灾害条件下Dijkstra算法进行了改进, 构建了惩罚因子函数, 结合GIS软件二次开发模块, 通过Visual C++6.0实现了复杂网络的分析功能。分析了重大灾害条件下节点数量对于道路可靠性以及最优路径选取的影响, 综合考虑距离、行程时间以及节点数量因素, 证明了改进Dijkstra算法对于最优路径选择的优越性。分析结果表明: 利用改进Dijkstra算法、经典Dijkstra算法计算出的路径节点数分别为31、59, 行程时间基本相同。可见, 改进算法能有效减少疏散路径中的节点数量, 降低车辆在节点处的延误损失和风险。
-
关键词:
- 最短路径 /
- Dijkstra算法 /
- 惩罚因子 /
- 可靠性分析
Abstract: The Dijkstra algorithm under large-scale disaster was improved by using classical Dijkstra algorithm, and the function of penalty factor was built. Complex network analysis function was realized by using Visual C++ 6.0 and the secondary development module of GIS. The impacts of node quantity on road reliability and the selection of optimal path under large-scale disaster were analyzed. Distance, travel time and node quantity were considered, the advantage of improved Dijkstra algorithm in the selection of optimal path was proved. Analysis result shows that the node quantities computed by improved Dijkstra algorithm and classical Dijkstra algorithm are 31, 59 respectively, travel times are almost same. So the improved algorithm can reduce the node quantity in evacuation route effectively, and decrease the delay loss and risk of vehicle at the node.-
Key words:
- shortest path /
- Dijkstra algorithm /
- penalty factor /
- reliability analysis
-
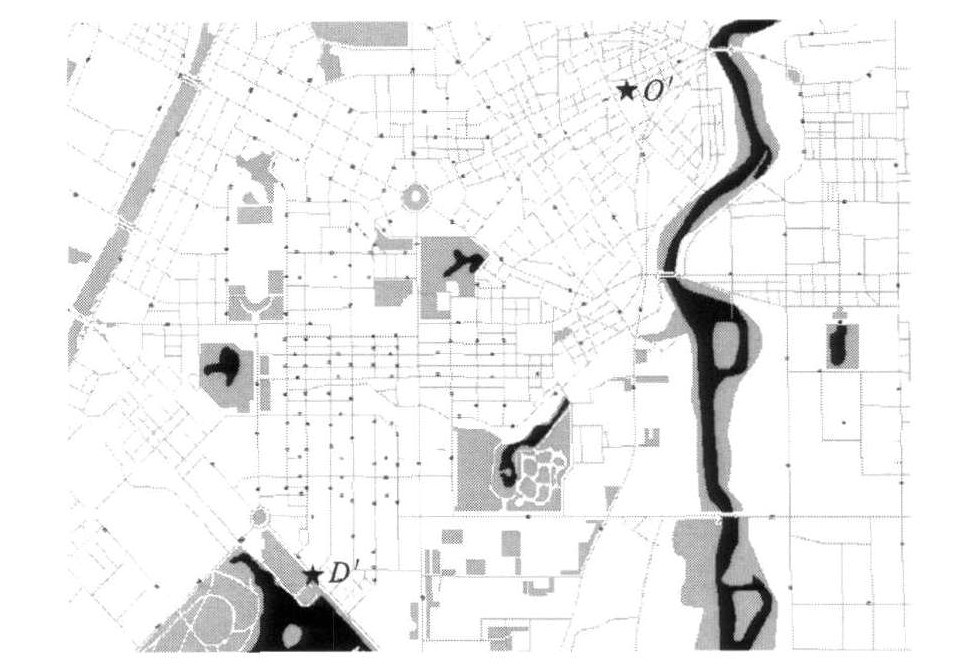
表 1 A、B两路径的比较
Table 1. Comparison of paths A and B
路径 路径A 路径B 包含节点数/个 59 31 行程时间/min 15.53 14.31 距离/km 6.625 6 6.675 9 
下载: 导出CSV
-
[1] HOFFMAN W, PAVLEY R. A method for the solution of the Nth best path problem[J]. Journal of the Association for Computing Machinery, 1959, 6 (4): 506-514. doi: 10.1145/320998.321004 [2] LAWLER E L. Combinatorial Opti mization: Networks and Matroids[M]. New York: Courier Dover Publications, 1976. [3] YAMADA T. A network flowapproach to a city emergency evacuation planning[J]. International Journal of Systems Science, 1996, 27 (10): 931-936. doi: 10.1080/00207729608929296 [4] DUNN C E, NEWTON D. Optimal routesin GIS and emergency planning applications[J]. Area, 1992, 24 (3): 259-267. [5] 王秀斌. GIS网络分析中最短路径的实现[J]. 测绘科学, 2007, 32 (5): 61-62. doi: 10.3771/j.issn.1009-2307.2007.05.021WANG Xiu-bin. Realization of the shortest path in GIS network analysis[J]. Science of Surveying and Mapping, 2007, 32 (5): 61-62. (in Chinese) doi: 10.3771/j.issn.1009-2307.2007.05.021 [6] CHERKASSKY B V, GOLDBERG A V, RADZIK T. Shortest paths algorithms: theory and experimental evaluation[J]. Mathematical Programming, 1996, 73 (2): 129-174. doi: 10.1007/BF02592101 [7] ZHAN F B, NOON C E. Shortest path algorithms: An evaluation using real road networks[J]. Transportation Science, 1998, 32 (1): 65-73. doi: 10.1287/trsc.32.1.65 [8] 王杰臣, 杨得志, 张伟. 最短路径问题的一种改进算法[J]. 解放军测绘学院学报, 1999, 16 (4): 282-285. https://www.cnki.com.cn/Article/CJFDTOTAL-JFJC199904014.htmWANG Jie-chen, YANG De-zhi, ZHANG Wei. An improvement algorithm of shortest route analysis[J]. Journal of the PLA Institute of Surveying and Mapping, 1999, 16 (4): 282-285. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JFJC199904014.htm [9] 成礼平. GIS技术在城市交通分配中的应用研究[D]. 南京: 东南大学, 2004.CHENG Li-ping. The research of applying GIS technology to city traffic assignment[D]. Nanjing: Southeast University, 2004. (in Chinese) [10] 夏松, 韩用顺. GIS中最短路径算法的改进实现[J]. 测绘通报, 2004 (9): 40-42. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB200409014.htmXI A Song, HAN Yong-shun. An improved implementation of shortest path algorithmin GIS[J]. Bulletin of Surveying and Mapping, 2004 (9): 40-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB200409014.htm [11] 严寒冰, 刘迎春. 基于GIS的城市道路网最短路径算法探讨[J]. 计算机学报, 2000, 23 (2): 210-215. doi: 10.3321/j.issn:0254-4164.2000.02.015YAN Han-bing, LIU Ying-chun. A new algorithm for finding shortcut in a city's road net based on GIS technology[J]. Chinese Journal of Computers, 2000, 23 (2): 210-215. (in Chinese) doi: 10.3321/j.issn:0254-4164.2000.02.015 -
点击查看大图
图(2) / 表(1)
计量
- 文章访问数: 557
- HTML全文浏览量: 63
- PDF下载量: 778
- 被引次数: 0
