Integrated simulation platform of braking system of rolling stock based on multi-discipline collaborative analysis
-
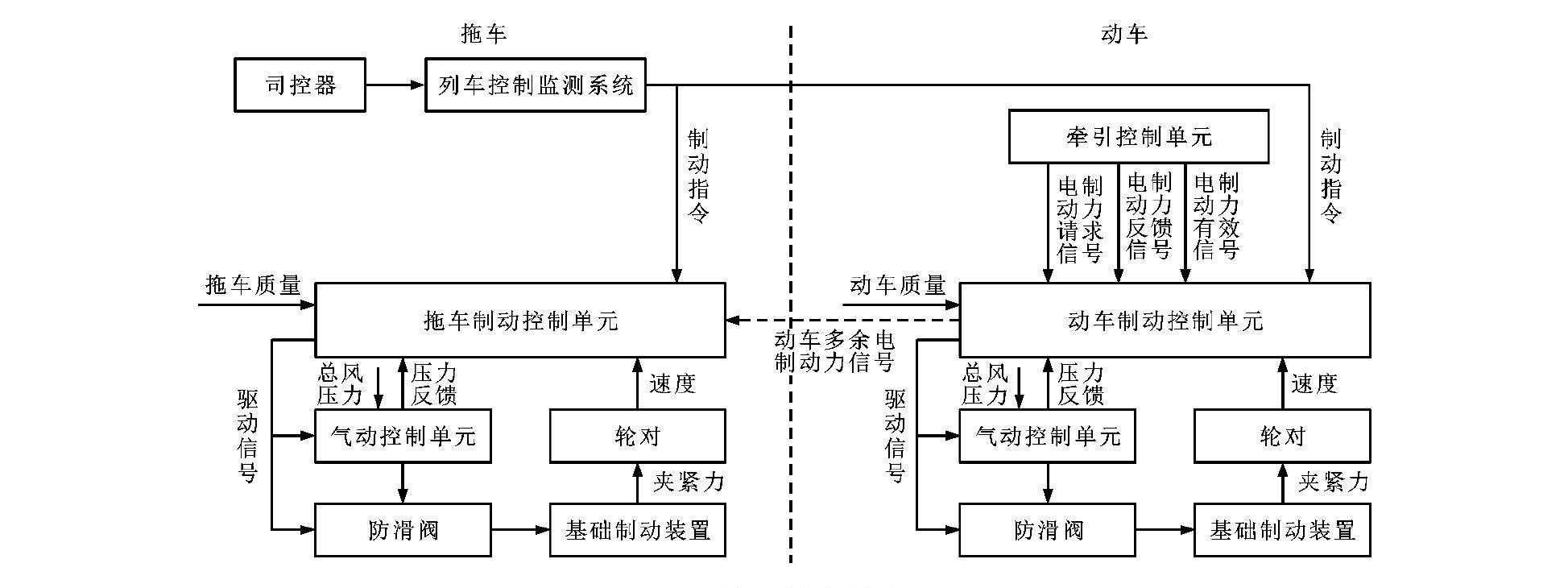
摘要: 根据轨道车辆电空复合制动的工作原理, 以全车制动系统为研究对象, 一动一拖制动控制单元为研究载体, 基于多学科协同分析方法, 建立了控制子系统、气制动子系统、电制动子系统与制动执行子系统模型, 基于各子系统之间的关联参数, 搭建了制动系统的联合仿真平台; 根据广佛二期车辆的实际参数, 模拟列车电制动失效工况下常用全制动的运行工况, 计算了空走时间、制动时间、制动距离、制动减速度、瞬时速度、平均减速度、纵向冲动、车钩力、利用黏着系数与制动缸压力, 并与试验结果进行了对比, 以验证集成化仿真平台的可行性和有效性。仿真和试验结果表明: 在制动稳定后, 仿真和试验的列车制动减速度约为1.25m·s-2, 仿真的平均减速度约为1.05m·s-2, 试验的平均减速度约为1.09m·s-2, 误差较小, 且均符合常用全制动的平均减速度不小于1.0m·s-2的要求; 在常用全制动工况下, 采取等磨耗制动力分配的动、拖车利用黏着系数不同, 动车约为0.13, 拖车约为0.12, 但都未超过0.16的最大可利用黏着系数的限制; 虽然动、拖车的质量不同, 但等磨耗工况下施加常用全纯空气制动后, 试验和仿真的动、拖车的制动缸压力均相等, 约为420kPa。由此可见, 可利用基于多学科协同分析的联合仿真平台对轨道车辆制动系统进行车辆级的研究, 为制动系统的开发和设计优化提供理论依据。Abstract: On the basis of the working principle of electro-pneumatic brake, the braking system of rolling stock was taken as research object, one motor car and one trailer were taken as a control unit, and the control subsystem model, air brake subsystem model, electric braking subsystem model and braking executing subsystem model were built based on multi-discipline collaborative analysis. By the correlation parameters of the subsystems, a co-simulation platform was established. The operating condition of full service braking was simulated under the failure of electric braking according to the actual parameters of second phase of Guangfo Metro, and the idling braking time, braking time, braking distance, braking deceleration, instantaneous speed, mean deceleration, longitudinal jerk, coupler force, adhesion utilization and braking cylinderpressure were calculated. The simulation and test results were compared to verify the feasibility and validity of the platform. Simulation and test results show that the braking decelerations of train in simulation and test are about 1.25 m·s-2 after braking process is steady, the mean braking deceleration in simulation is about 1.05 m·s-2, the decelerate in test is about 1.09 m·s-2, all of them meet the requirement that the mean braking deceleration of full service braking is more than 1.0 m·s-2, and the simulation error is lesser. In full service braking, the adhesion utilizations are different under the equivalent wear braking force distribution strategy, it is 0.13 for motor car and 0.12 for tailor, but both of them are less than the adhesion limited 0.16. Although the qualities of motor car and trailer car are different, the pressures of braking cylinders in full service braking are same under the equivalent wear strategy, and the value is about 420 kPa. In summary, the multi-discipline collaborative analysis and co-simulation platform are effective in modelling and analyzing the braking system of rolling stock, and are theoretical basis to research and develop braking system.
-
Key words:
- rolling stock /
- braking system /
- multi-discipline analysis /
- integrated simulation /
- braking performance
-
0. 引言
随着轨道车辆速度的提高, 制动系统对保证列车的安全越来越重要, 早期的制动系统开发与设计一直采用试验的方法对其结构、控制和性能进行研究和优化。由于现代动车组与重载运输的快速发展, 制动系统越来越复杂, 传统的试验方式会耗费大量的人力和物力, 已经不能满足制动系统的研发与设计要求。随着计算机性能的提高, 当前多采用数值仿真的方法进行制动性能的研究。Murtaza等建立了列车管和分配阀模型, 用有限差分法求解了列车管气体流动的一维偏微分方程组[1-3]; Pugi等利用模块化建模的思想, 按照建模对象的复杂程度将列车制动系统分成基本元件库、复杂元件库与车辆元件库, 并采用MATLAB/Simulink建立了各个元件库的系统模型[4], 并且通过AMESim建立了货车制动系统的分配阀和列车管模型等[5]; Cantone等将制动系统的制动阀、分配阀等视为“黑箱”, 利用试验数据拟合函数进行建模[6]; Piechowiak等建立了整个货车制动系统的数学模型, 包括列车管模型、分配阀模型、制动缸模型与一些气动模型中基本的流体元件模型(如缩孔与腔体模型等), 并通过试验测量了货车制动系统模型的所有参数[7-8]; 魏伟等利用数值计算的方法建立了货车的制动系统模型, 采用特征线法进行求解, 并分析了其制动特性[9-10]; 陈哲明等使用MATLAB/Simulink建立了制动缸压力的非线性简化模型和四分之一车体模型, 并对高速动车组防滑控制进行了仿真[11-12]; 陆强等利用AMESim建立了轨道交通车辆制动系统的简化模型[13]; 左建勇等利用AMESim建立了地铁车辆的空气制动系统模型, 进行了常用制动、紧急制动与阶段制动的制动系统功能仿真, 并通过试验对模型进行了验证[14-15]。
以上制动系统的建模方法多是采用单一学科的建模方法, 对制动系统中的气制动子系统或控制子系统的工作原理进行分析, 不能建立车辆级的制动特性分析方法。当前轨道车辆普遍采用微机控制直通电空制动系统, 采用电制动和空气制动协调配合的复合制动方式, 实现一个制动单元甚至整列车制动能力的充分利用。基于此, 本文以轨道车辆制动系统为主要研究对象, 结合列车制动动力学理论, 以制动单元为研究载体, 基于多学科协同分析的方法, 分别建立制动系统的控制子系统、气制动子系统、基础制动子系统与制动动力学子系统等模型, 基于各个子系统之间的相互关联参数, 搭建联合仿真平台, 从车辆级的角度对制动系统进行研究; 以广佛地铁二期车辆为例, 根据其实际车辆参数建立轨道车辆制动系统的多学科协同分析集成化仿真平台, 进行制动性能仿真分析, 并与试验结果进行对比, 以验证该平台的有效性和可行性。
1. 轨道车辆制动系统工作原理
当前轨道车辆多采用微机控制直通电空制动系统, 主要由制动指令、传输单元、制动控制系统、气动控制单元、电制动控制单元、基础制动装置、防滑控制单元、供风单元与列车管路等组成。采用电制动和空气制动相结合的复合制动方式, 一般以一辆动车和一辆拖车作为一个制动单元进行控制, 结构原理见图 1。制动控制装置通过列车控制监测系统接收来自司机制动控制器或自动列车保护的制动指令, 进行制动力分配、电空配合和防滑控制等, 完成列车的制动过程。
2. 基于多学科协同分析的制动系统仿真平台
多学科协同分析方法又称为多领域系统的联合仿真方法, 是指在不同专业软件环境下, 建立诸如多体动力学子系统模型、控制子系统模型与气(液) 压子系统模型等, 将它们构成开环或闭环系统的整机模型进行仿真, 既可以把研究重点集中在子系统的细节上, 又可以考虑到系统的整体性能[16]。
目前, 对于轨道车辆制动系统, 单领域内的仿真软件已经相当成熟。由于涉及多个学科领域, 要在同一个仿真领域内实现制动系统的完整、准确的仿真有一定的难度, 所以可以考虑充分发挥各软件的专业领域仿真功能, 通过多种软件协同分析实现制动系统的整体性能。本文以微机控制直通电空制动系统为例, 针对轨道车辆制动系统电空复合制动的特点, 基于多学科协同分析的方法, 结合制动动力学模型, 将制动系统分为控制子系统、气制动子系统与制动执行子系统, 基于MATLAB/Simulink建立了制动系统的控制子系统模型和基础制动模型, 采用AMESim建立了气制动子系统模型, 采用多体动力学软件SIMPACK建立了列车制动动力学模型。由于多体动力学软件SIMPACK和气液压仿真软件AMESim都分别提供了与Simulink间的接口, 方便实现软件之间的协同仿真运行, 因此, 本文选取Simulink作为主仿真环境平台, 在各专业软件中建立子系统模型的基础上, 利用软件提供的接口程序生成连接文件, 并根据各子系统之间的参数耦合关系将各子模块组合成制动系统的整体仿真模型, 搭建了联合仿真平台, 见图 2。
3. 子系统模型与联合仿真平台搭建
3.1 气制动子系统模型
微机控制直通电空制动系统的气制动子系统主要包括电空转换阀(Electro-Pneumatic Valve, 简称EP阀)、中继阀、紧急阀、空重车阀、防滑阀、制动缸和制动管路等[15], 其中紧急阀可采用AMESim中的通用电磁阀模拟, EP阀、防滑阀、中继阀与空重车阀需要通过对AMESim二次开发实现。EP阀是电空直通制动系统的关键部件之一, 其作用是根据制动控制指令调节中继阀容积室的输出压力。目前, 在列车制动领域常用的为开关型EP阀, 主要由制动电磁阀、缓解电磁阀、压力传感器、容积室和控制器等组成[17], 见图 3, P为压力。其工作原理是: 当得到制动指令后, 制动电磁阀得电, 阀口打开, 预控压力经EP阀传给后面的部件, 同时压力传感器反馈预控压力信号, 如果压力信号低于指令值, 则制动电磁阀得电充气, 如果高于指令值, 则缓解电磁阀得电排气, 直至压力信号达到指令值。通过制动和缓解电磁阀的通断电, 可实现预控压力的升高或下降, 最终使目标制动缸压力满足制动要求。开关型EP阀由于容积效应与气体流动惯性的影响, 仅采用基本的开关控制, 动态响应和控制精度达不到制动要求, 在实际工程中多使用脉冲宽度调制信号进行控制, 本文进一步采用PID反馈控制的方式, 在AMESim中对EP阀进行了建模, 如图 4所示, V表示管路体积, 该EP阀模型具有理想的动态响应和控制精度。采用类似的方法使用AMESim分别建立了上述其他气动阀件和元件模型, 气路信息通过气动元件之间的管路连接。搭建出的一动一拖列车制动系统的气制动子系统模型见图 5: PT与PM分别为拖车和动车的目标压力输入; P1~P4为拖车的1~4轴制动缸压力信号, P5~P8为动车的1~4轴制动缸压力信号; I1~I8为拖车的防滑阀控制电流信号; I9~I16为动车的防滑阀控制电流信号。
通过对常用制动、紧急制动、阶段制动和缓解等制动工况的模拟, 对建立的气制动系统模型进行验证, 分析制动时间与压力等参数在制动过程中的变化特性[15], 见图 6。图 6(a) 为常用制动工况的仿真结果, 设定常用制动的CV压力为250kPa, 0~0.4s为缓解状态, 0.4~3.5s为常用制动状态, 3.5s后再次缓解至结束。可以看出: CV压力变化比制动缸压力变化响应快, 在制动缓解时, CV压力比制动缸压力下降快, 两者最大延时不超过0.5s。图 6(b) 为紧急制动工况仿真结果, CV压力设定为500kPa, 仿真结果表明: 紧急制动与常用制动时的CV压力变化和制动缸压力变化趋势一致, 但紧急制动时的制动缸压力上升速率比常用制动快, 紧急制动时制动缸压力上升至目标压力需1.6s, 而常用制动需要2.0s。图 6(c) 为阶段制动和阶段缓解下的制动工况仿真结果, 可见: 在阶段制动与阶段缓解过程中, 制动缸压力比CV压力的响应滞后, 这一点与常用制动与紧急制动的仿真结果一致, 并且无论是在阶段制动还是阶段缓解, 制动缸压力都能够随着CV压力的变化而变化, 具有很好的跟随性。验证结果表明: 所建立的气制动子系统模型可用于制动系统联合仿真。
3.2 控制子系统模型
当前轨道车辆的制动控制方式采用的是电空配合的复合运算式控制方式, 轨道车辆的制动控制策略主要指常用与紧急制动工况下的电空制动力分配与电空配合策略等, 主要由制动电子控制单元实现制动系统的控制功能。轨道车辆的制动单元中有动车与拖车, 制动时需要在各车辆之间进行协调, 因此, 采用的制动控制策略也不同, 常用的方式有均衡制动控制和空气制动滞后控制[18]。均衡制动控制是各车辆承担自身所需制动力, 此时动车优先使用电制动力, 不足部分采用空气制动力, 拖车完全采用空气制动力, 可以看出: 均衡制动控制的拖车制动闸片磨耗要远大于动车, 动车的电制动力不能得到充分利用, 因此, 现在较少使用这种制动控制方式。空气制动滞后控制是指在制动单元内的车辆间, 当动车的电制动力达到最大值之前, 优先使用电制动力, 电制动力不足部分由空气制动力承担。根据等黏着或等磨耗进行空气制动力补足的2种不同原则, 空气制动滞后控制又可分为拖车空气制动优先补足控制和动车与拖车空气制动均衡补足控制, 当前轨道车辆使用较多的为拖车空气制动优先补足的制动控制方式。以一动一拖的制动单元为例, 图 7、8分别为空气制动滞后控制方式下的动车、拖车的制动控制流程。本文基于以上的制动控制策略, 使用MATLAB/Simulink搭建了制动力分配和电空配合模块、制动减速度曲线和载荷处理模块等。
3.3 制动动力学模型
从动力学的观点来看, 轨道车辆模型是由多个刚体铰接组成的多体系统, 是一个庞大复杂的机械系统, 为了减少仿真计算的求解时间, 需要先将其模型进行合理而必要的简化, 再将简化后的模型分解为SIMPACK中的一些基本要素, 比如体、铰接、约束与力元等。主要考虑了黏着力模型、轮对、转向架、车体、悬挂系统、基础制动装置与车钩等子模型的建模, 车体、构架和轮对一般作为刚体考虑, 并根据它们的质量特性分别进行定义; 悬挂系统与减振器等部件, 在建模时通常考虑为力元, 其中一系悬挂力元和二系悬挂力元包括刚度和阻尼; 铰接主要指约束各个刚体之间的相对运动关系, 车体和转向架之间采用SIMPACK中的0号铰接, 轮对和轨道之间采用了SIMPACK中专用于轨道车辆轮轨的7号铰接。以一动一拖为例建立的轨道车辆的拓扑关系见图 9[19-21]。根据车辆动力学理论, 使用多体动力学软件SIMPACK建立了列车制动单元动力学模型或整列车纵向动力学模型见图 10。
3.3.1 黏着力模型
由于轨道车辆制动过程中轮轨间的黏着属于大蠕滑工况, 因此, 黏着力计算采用Polach模型, 可以准确地计算轮轨处于稳定和滑行状态下的黏着力[22-24], 为
式中: F为黏着力; Q为正压力; f为轮轨间摩擦因数; ε为黏着区的切向应力梯度; k1、k2分别为黏着区和滑移区的调节参数; C为接触刚度; a、b分别为椭圆接触斑长、短半轴长度; s为总蠕滑率; s1、s2分别为纵向和横向蠕滑率; G为剪切弹性模量; c为量纲为1的Kalker系数。
3.3.2 车钩缓冲器模型
为了尽量与实际情况一致, 考虑了车钩间隙, 钩缓装置的拉压特性曲线见图 11: p为车钩力; l为行程; L为缓冲器最大行程; δ为车钩间隙。以某型轨道车辆使用的车钩缓冲器为例, 其最大行程L为58mm时, 最大车钩力pmax为590kN。当相邻两车相对位移大于车钩间隙而又小于缓冲器行程时, 车钩力按照钩缓装置增载曲线上升, 按卸载曲线下降; 相对位移超过这一范围时, 钩缓装置被压死, 车钩力则按照车体刚度加、卸载。
3.4 联合仿真平台搭建
分别建立制动控制子系统模型、气制动子系统模型和一动一拖车辆单元制动动力学模型, 以Simulink为主仿真环境, 搭建了基于多学科协同分析的制动系统集成化仿真平台, 见图 12。图 12中: K1~K4为拖车的1~4轴的制动装置所受的夹紧力; K5~K8为动车的1~4轴的制动装置所受的夹紧力; v、d、D、J、Jmax、
4. 制动过程仿真与试验结果分析
以广佛地铁二期车辆为例进行建模与仿真分析, 地铁车辆为4节编组, 编组型式为: =T1-M1-M2-T2= (其中T表示拖车, M表示动车, =表示全自动车钩, -表示半永久式牵引杆), 以一动一拖为一个制动单元。常用制动和快速制动采用空气制动和电制动配合的复合制动方式, 优先使用电制动力, 当电制动力不能满足制动力需求时, 采用等磨耗补充方式, 将需要补充的空气制动力在制动单元内平均分配, 即动车、拖车均施加相同的空气制动力, 该制动方式下动车、拖车的制动缸压力基本一致。在接近零速时, 进入保压制动模式(制动缸压力逐渐减小为最大常用制动压力的70%), 直至列车停稳。
列车最高运行速度为80km·h-1, 在平直干轨条件下, 要求常用全制动平均减速度不小于1.0m·s-2, 紧急制动和快速制动下平均减速度不小于1.2m·s-2; 常用制动要求的制动冲动限制不大于0.75m·s-3, 紧急制动时不大于1m·s-3; 最大常用制动减速度完成的制动距离不大于247m;无论是电空配合或是纯空气制动, 利用黏着系数均不超过0.16。
4.1 制动过程仿真
根据车辆的实际参数, 基于多学科协同仿真方法, 建立了各个子系统模型, 其中部分仿真参数见表 1; 搭建了多学科协同分析的制动系统集成化仿真平台, 进行了常用制动与紧急制动等制动工况的仿真模拟, 分析了空走时间、动拖车制动缸压力、制动瞬时速度、瞬时减速度、制动冲动、制动距离、制动时间、平均减速度与纵向冲动等参数在制动过程中的变化特性; 以AW3工况(包括车辆质量与最大载荷质量之和的载荷状态工况)[25]下常用全制动的纯空气制动过程(模拟电制动失效) 为例, 对比了仿真结果与试验结果, 验证了联合仿真平台的可行性和有效性。仿真结果见图 13~17, 制动性能对比见表 2。
表 1 部分仿真参数Table 1. Some simulation parameters
图 13为制动缸压力的仿真结果: 由于采取等磨耗的空气制动力补充方式, 动拖车的制动缸压力基本相等, 约为420kPa; 接近零速时, 列车进入保压模式, 制动缸压力约为294kPa, 约为常用全制动的70%;其中空走时间为1.88s, 制动时间为19.72s, 见表 2。
图 14为车辆瞬时速度和减速度曲线: 由于气制动系统的压力建立需要一定的时间, 随着制动缸压力的上升, 减速度(绝对值) 逐渐增大, 速度逐渐降低; 制动过程稳定后, 减速度趋于一定值, 约为1.25m·s-2; 进入保压模式后, 制动缸压力逐渐下降, 减速度(绝对值) 逐渐减小。
表 2 制动性能比较Table 2. Comparison of braking performances
图 15、16分别为制动过程中的纵向冲动和车钩力的仿真结果, 可知: 随着制动缸压力的上升, 纵向冲动和车钩力(绝对值) 逐渐增大; 制动稳定后, 钩缓装置吸收了纵向冲动的能量, 纵向冲动趋于零; 由于制动控制中采取了等磨耗的空气补充方式, 动拖车施加相同的制动缸压力而产生大小相同的制动力, 但前面拖车相比后面的动车载荷较小, 车钩受到了约为4.5kN的压钩力。
图 17为动拖车的利用黏着系数: 由于采用等磨耗的制动力分配方式, 制动过程稳定后, 动车利用黏着系数约为0.13, 拖车利用黏着系数约为0.12, 均未超过最大利用黏着系数限制0.16。
4.2 试验验证
为了检验地铁车辆的制动性能, 分别在T1车底加装测速雷达采集列车速度, 如图 18所示; 在T1车的二位转向架、M1车的一位转向架的制动控制单元测试接口加装压力传感器采集制动缸压力, 如图 19所示; 图 20为试验数据采集设备, 进行了AW3工况正线运行条件下的制动性能试验。实际的车钩力不易测试, 因此, 未能给出试验结果和仿真进行对比。试验结果见图 21~23, 制动性能对比见表 2。
图 21为制动缸压力的试验结果: 动拖车的制动缸压力基本相等, 约为422kPa; 接近零速的时候, 列车进入保压模式, 制动缸压力约为289kPa, 约为常用全制动的68%;空走时间为1.85s, 制动时间为18.15s, 见表 2。
图 22为车辆瞬时速度和减速度曲线: 随着制动缸压力的上升, 减速度(绝对值) 逐渐增大, 速度逐渐降低; 制动过程稳定后, 减速度在1.28m·s-2上下波动; 并且随着速度的降低, 瞬时减速度趋于变大, 主要是由于在实际的制动过程中闸瓦摩擦因数随着速度的降低在逐渐增大, 导致实际的制动力大于目标制动力造成的。
图 23为制动过程中的纵向冲动的试验结果, 可知: 随着制动缸压力的上升, 纵向冲动在逐渐增大, 最大值不大于0.75 m·s-3, 符合常用制动的冲动限制要求; 列车在实际的运行过程中还会受到坡道坡度、闸瓦摩擦因数等不确定参数的影响, 因此, 制动稳定后, 纵向冲动仍有一定的波动, 在0上下波动, 但该波动较小, 不影响列车的乘坐舒适性。
4.3 仿真和试验结果对比分析
由图 13~17、21~23与表 2的对比可知: 制动缸压力、空走时间、制动时间与制动距离的仿真和试验结果基本一致; 制动初速度为80km·h-1的常用全制动工况下制动距离均小于247m, 平均减速度均大于1m·s-2, 纵向冲动均不大于0.75m·s-3, 符合常用全制动的校核要求, 验证了基于多学科协同分析的制动系统集成化仿真平台进行制动系统性能分析的可行性和有效性。
由仿真和试验结果比较可知: 虽然制动缸压力基本相等, 但仿真得到的制动时间和制动距离小于试验结果, 而平均减速度的仿真结果大于试验结果, 这主要是由于实际列车的闸瓦摩擦因数会因速度的降低而升高, 但是制动控制系统在计算目标制动缸压力时, 一般选取一个较低的平均摩擦因数。这样在制动过程中, 实际闸瓦摩擦因数要高于制动系统用于计算的定值摩擦因数, 从而使实际的制动力偏大, 因而实测的平均减速度偏大, 制动时间减小, 制动距离缩短, 图 22的瞬时减速度的试验值在低速时逐渐增大的趋势也说明了这一现象, 因此, 后期应当根据摩擦副的摩擦因数-速度关系试验曲线对模型进行修正, 使得仿真结果更符合实际的制动过程。
通过多学科协同分析的联合仿真平台可以从车辆级的角度对轨道车辆的制动性能进行仿真分析, 可以得到空走时间、制动时间、制动距离、制动减速度、瞬时速度、平均减速度、纵向冲动、车钩力、利用黏着系数与动拖车的制动缸压力等, 可以对轨道车辆制动过程的制动力分配、电空配合策略与防滑控制等进行研究, 相对于文献[11]~[15]中仅考虑气制动子系统的传统制动仿真来说, 本文提出的轨道车辆制动系统的多学科协同分析方法更具有优越性。
5. 结语
(1) 针对轨道车辆的制动系统, 基于多学科协同分析构建了制动系统的联合仿真平台, 为制动系统的协同研发和动态分析提供了集成化仿真平台, 可以从车辆级的角度对轨道车辆的制动性能进行研究。
(2) 多学科协同分析方法既可应用于地铁车辆, 亦可应用到高速动车组制动系统的性能分析, 并通过仿真和试验结果的对比分析, 验证了基于多学科协同分析的轨道车辆制动系统联合仿真平台的有效性和可行性。
(3) 轨道车辆的实际制动过程会受到摩擦副的摩擦因数与坡道坡度等不确定参数的影响, 应当根据摩擦因数的试验曲线, 并考虑实际线路的条件对制动系统进行建模分析。
(4) 下一步的研究重点是根据电制动力的试验曲线, 继续完善联合仿真平台的子系统模型, 考虑不同工况下不确定因素的影响, 进行轨道车辆的电空配合优化和防滑控制研究, 并将优化算法应用于动车组。
-
[1] MURTAZA M A, GARG S B L. Brake modelling in train simulation studies[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1989, 203 (1): 87-95. [2] MURTAZA M A, GARG S B L. Transients during a railway air brake release demand[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1990, 204 (1): 31-38. doi: 10.1243/PIME_PROC_1990_204_183_02 [3] MURTAZA M A. Railway air brake simulation: an empirical approach[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207 (1): 51-56. doi: 10.1243/PIME_PROC_1993_207_226_02 [4] PUGI L, MALVEZZI M, ALLOTTA B, et al. A parametric library for the simulation of a Union International des Chemins de Fer (UIC) pneumatic braking system[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218 (2): 117-132. doi: 10.1243/0954409041319632 [5] PUGI L, PALAZZOLO A, FIORAVANTI D. Simulation of railway brake plants: an application to SAADKMS freight wagons[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2008, 222 (4): 321-329. doi: 10.1243/09544097JRRT118 [6] CANTONE L, CRESCENTINI E, VERZICCO R, et al. A numerical model for the analysis of unsteady train braking and releasing maneuvres[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223 (3): 305-317. doi: 10.1243/09544097JRRT240 [7] PIECHOWIAK T. Pneumatic train brake simulation method[J]. Vehicle System Dynamics, 2009, 47 (12): 1473-1492. doi: 10.1080/00423110802600946 [8] PIECHOWIAK T. Verification of pneumatic railway brake model[J]. Vehicle System Dynamics, 2010, 48 (3): 283-299. doi: 10.1080/00423110902780622 [9] 魏伟, 张开文. 列车空气制动系统的数学模型[J]. 西南交通大学学报, 1994, 29 (3): 286-291. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT403.009.htmWEI Wei, ZHANG Kai-wen. A mathematical model of air brake system of trains[J]. Journal of Southwest Jiaotong University, 1994, 29 (3): 286-291. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT403.009.htm [10] 魏伟, 赵旭宝, 姜岩, 等. 列车空气制动与纵向动力学集成仿真[J]. 铁道学报, 2012, 34 (4): 39-46. doi: 10.3969/j.issn.1001-8360.2012.04.007WEI Wei, ZHAO Xu-bao, JIANG Yan, et al. The integrated model of train air brake and longitudinal dynamics[J]. Journal of the China Railway Society, 2012, 34 (4): 39-46. (in Chinese). doi: 10.3969/j.issn.1001-8360.2012.04.007 [11] 陈哲明, 曾京, 罗仁. 列车空气制动防滑控制及其仿真[J]. 铁道学报, 2009, 31 (4): 25-31. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200904007.htmCHEN Zhe-ming, ZENG Jing, LUO Ren. Wheel-slip prevention control and simulation under train pneumatic braking[J]. Journal of the China Railway Society, 2009, 31 (4): 25-31. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200904007.htm [12] 罗仁, 曾京. 铁道车辆防滑控制仿真[J]. 机械工程学报, 2008, 44 (3): 29-34. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200803007.htmLUO Ren, ZENG Jing. Anti-sliding control simulation of railway vehicle braking[J]. Chinese Journal of Mechanical Engineering, 2008, 44 (3): 29-34. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200803007.htm [13] 陆强, 杨美传. 基于AMESim的地铁车辆空气制动系统的建模及仿真[J]. 液压气动与密封, 2011 (10): 45-48. https://www.cnki.com.cn/Article/CJFDTOTAL-YYQD201110017.htmLU Qiang, YANG Mei-chuan. Modeling and simulation methodology of pneumatic braking system in motro vehicles using AMESim[J]. Hydraulics Pneumatics and Seals, 2011 (10): 45-48. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YYQD201110017.htm [14] 左建勇, 任利惠, 吴萌岭. 铁道车辆制动系统防滑控制仿真与试验研究[J]. 同济大学学报: 自然科学版, 2010, 38 (6): 912-916. doi: 10.3969/j.issn.0253-374x.2010.06.023ZUO Jian-yong, REN Li-hui, WU Meng-ling. Simulation and experimental research on anti-sliding control of railway vehicle braking[J]. Journal of Tongji University: Natural Science, 2010, 38 (6): 912-916. (in Chinese). doi: 10.3969/j.issn.0253-374x.2010.06.023 [15] 左建勇, 王宗明, 吴萌岭. 地铁列车空气制动系统仿真模型[J]. 交通运输工程学报, 2013, 13 (2): 42-47. http://transport.chd.edu.cn/article/id/201302006ZUO Jian-yong, WANG Zong-ming, WU Meng-ling. Simulation model of air Braking system for subway train[J]. Journal of Traffic andTransportation Engineering, 2013, 13 (2): 42-47. (in Chinese). http://transport.chd.edu.cn/article/id/201302006 [16] 朱德泉. 基于联合仿真的机电液一体化系统优化设计方法研究[D]. 合肥: 中国科学技术大学, 2012.ZHU De-quan. Study on optimization design method for mechanical-electrical-hydraulic integrated system based on collaborative simulation[D]. Hefei: University of Science and Technology of China, 2012. (in Chinese). [17] 刘建, 杨美传, 夏海龙. 基于AMESim的开关型EP阀仿真研究[J]. 铁道车辆, 2014, 52 (4): 12-14. https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL201404004.htmLIU Jian, YANG Mei-chuan, XIA Hai-long. Simulation research on the on-off EP valves based on AMESim[J]. Rolling Stock, 2014, 52 (4): 12-14. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDCL201404004.htm [18] 许志泉. 基于AMESim动车组空气制动系统仿真与研究[D]. 成都: 西南交通大学, 2013.XU Zhi-quan. Simulation and study on air brake system of EMU based on AMESim[D]. Chengdu: Southwest Jiaotong University, 2013. (in Chinese). [19] 缪炳荣, 肖守讷, 金鼎昌. 应用SIMPACK对复杂机车多体系统建模与分析方法的研究[J]. 机械科学与技术, 2006, 25 (7): 813-816. https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX200607015.htmMIAO Bing-rong, XIAO Shou-ne, JIN Ding-chang. Research on modeling and analysis of a complex multibody system by using SIMPACK[J]. Mechanical Science and Technology, 2006, 25 (7): 813-816. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX200607015.htm [20] 陈龙, 方宇, 潘以成, 等. 基于SIMPACK的城市轨道车辆脱轨安全性分析[J]. 城市轨道交通研究, 2013, 16 (8): 126-129, 133. https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201308029.htmCHEN Long, FANG Yu, PAN Yi-cheng, et al. Safety analysis of urban rail vehicle derailment based on SIMPACK[J]. Urban mass Transit, 2013, 16 (8): 126-129, 133. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201308029.htm [21] 黄安宁. 基于SIMPACK的某型轨道车辆动态性能仿真研究[D]. 昆明: 昆明理工大学, 2012.HUANG An-ning. Simulation research on dynamic performances of a certain type of railway vehicles based on SIMPACK[D]. Kunming: Kunming University of Science and Technology, 2012. (in Chinese). [22] POLACH O. Creep forces in simulations of traction vehicles running on adhesion limit[J]. Wear, 2005, 258 (7/8): 992-1000. [23] POLACH O. Fast wheel-rail forces calculation computer code[J]. Vehicle System Dynamics, 2000, 33 (S): 728-739. [24] MELI E, RIDOLFI A, RINDI A. An innovative degraded adhesion model for railway vehicles: development and experimental validation[J]. Meccanica, 2014, 49 (4): 919-937. [25] 许桂红. 地铁制动系统的研究与仿真[D]. 成都: 西南交通大学, 2014.XU Gui-hong. Research and simulation of metro braking system[D]. Chengdu: Southwest Jiaotong University, 2014. (in Chinese). 期刊类型引用(6)
1. 翟耕慰，田春，马天和，陈超，王国壮. 基于减速度包络线修正的新型防滑效率计算方法. 交通运输工程学报. 2024(02): 193-206 . 
本站查看2. 李中奇，黄琳静，周靓，杨辉，唐博伟. 高速列车滑模自抗扰黏着控制方法. 交通运输工程学报. 2023(02): 251-263 . 本站查看3. 朱文健，余朝刚，朱文良. 轨道车辆制动防滑控制系统数值建模与验证. 机械科学与技术. 2023(10): 1727-1734 . 
百度学术4. 朱文良，郑树彬，吴娜，尧辉明，吴萌岭. 适用于制动工况下的轮轨低黏着改进模型. 铁道学报. 2021(03): 34-41 . 百度学术5. 朱文良，周嘉俊，孔靖森，郑树彬，吴萌岭. 动车组制动防滑控制建模仿真与试验研究. 城市轨道交通研究. 2020(12): 50-55 . 百度学术6. 陈旭，赵建飞，李毅. 地铁车辆纯空气制动滑行研究. 铁路技术创新. 2019(05): 37-44 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 800
- HTML全文浏览量: 232
- PDF下载量: 540
- 被引次数: 11
