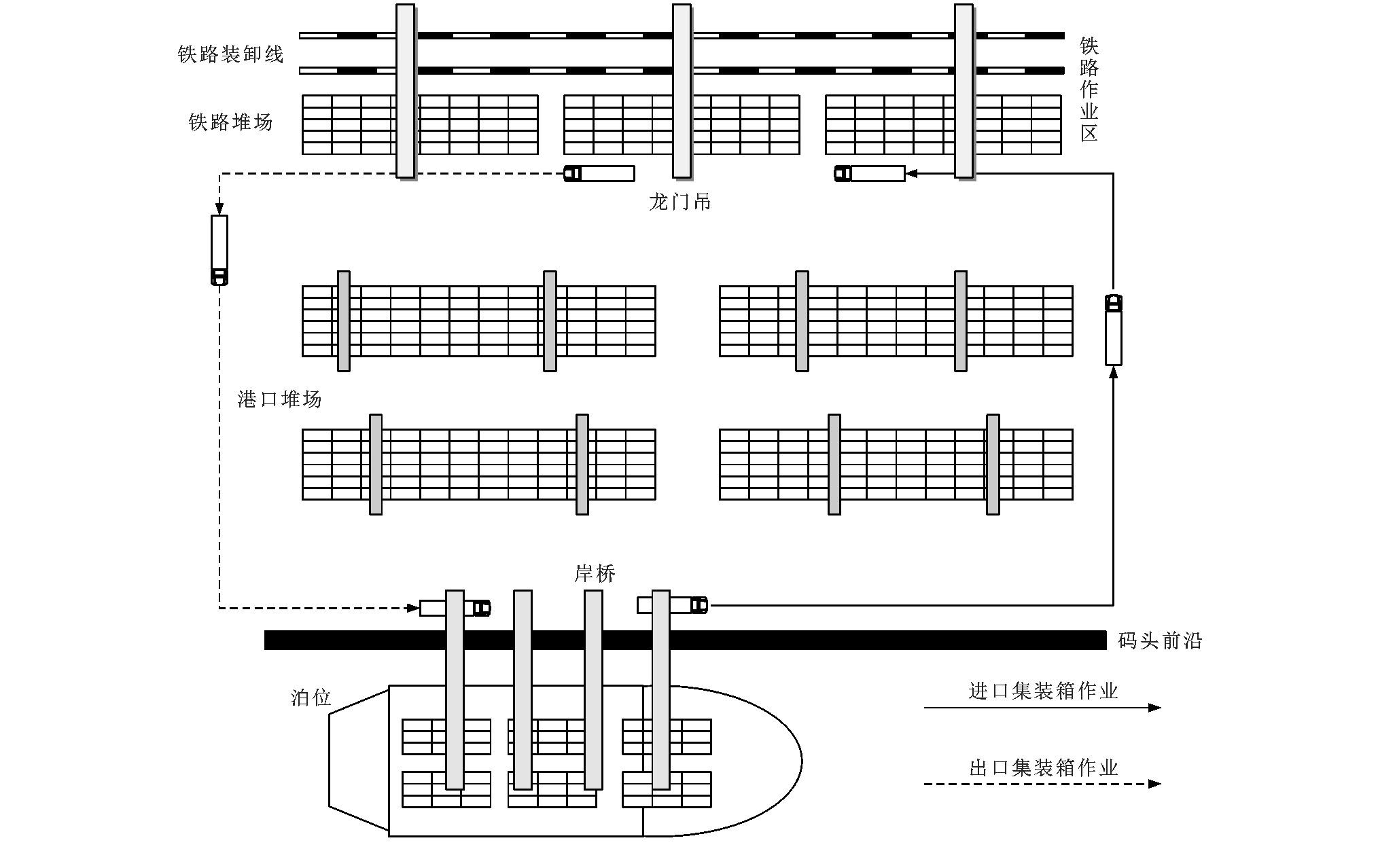
Integrated scheduling of handling operation between train and vessel in container terminal under uncertain factor
Article Text (Baidu Translation)
-
摘要: 为了提高集装箱码头的效率, 建立了集装箱码头车船装卸作业集成调度模型; 考虑了装卸同步作业与一些实际约束条件, 如岸桥、龙门吊间干扰和安全距离等, 以及生产调度中的不确定因素, 如岸桥、集卡的速度变化等, 设计了改进的多层遗传算法求解模型; 为了确定随机变量的具体值, 在传统的遗传算法中引入蒙特卡罗法, 为了使得集装箱在集卡间均衡分配, 在传统的遗传算法中引入均衡算子; 通过试验验证模型和算法的可行性和有效性, 并进行了改进的多层遗传算法中引入均衡算子与未引入均衡算子间的对比试验。分析结果表明: 引入均衡算子后的装卸作业完成总时间为7 437.8s, 比未引入均衡算子减少760.3s, 且在引入均衡算子的试验中50FEU集装箱均匀分配给了5辆集卡, 而在未引入均衡算子的试验中未能均匀分配; 固定龙门吊和岸桥数量, 改变集卡的数量, 通过比较每组试验中作业总完成时间和边际效益值, 得出当集装箱数量为80、90、100FEU时, 最优设备配比为3台龙门吊、10辆集卡和4台岸桥。可见, 改进的多层遗传算法可以提高集装箱码头车船装卸作业的效率, 是解决集装箱装卸作业集成调度问题的一种有效方法。Abstract: To improve the efficiency of container terminals, an integrated scheduling model of handling operations between trains and vessels was established. Loading and unloading synchronization, as well as some practical constraints, such as quay crane (QC) interference, gantry crane (GC) interference, QC safety distance, GC safety distance and so on, were considered.Some uncertain factors during production scheduling, such as the change of QC speed and inner truck (IT) speed and so on, were also considered.In order to solve the model, an improved multi-layer genetic algorithm (MLGA) was developed.To determine the value of random variable, Monte Carlo method was introduced into the traditional genetic algorithm.To balance the allocation of containers among ITs, a balanced operator was introduced into traditional genetic algorithm.The feasibility and effectiveness of the proposed model and algorithm were verified by using computational experiments, and a comparison experiment wascarried out between the improved MLGAs with and without balanced operator.Analysis result indicates that the makespan of handling operation with balanced operator is 7 437.8 sand 760.3 s less than that without balanced operator.Meanwhile 50 FEU containers are evenly allocated to 5 ITs in the experiment with balanced operator, while in the experiment without balanced operator, they are unevenly assigned to ITs.Fixing the number of GCs and QCs, and changing the number of ITs, when the number of containers is 80, 90, and 100 FEU, respectively, the best equipment proportions are 3 GCs, 10 ITs and 4 QCs by comparing the makespans and marginal benefit values in each group of experiments.The efficiency of handling operations between trains and vessels in container terminals is enhanced by using improved MLGA, and the improved MLGA can be an effective approach to solve the integrated scheduling problem of container handling operation.
-
图 1 集装箱码头车船间装卸作业过程
Figure 1. Handling operation process between trains and vessels in container terminal
图 7 引入均衡算子前后作业完成总时间对比
Figure 7. Comparison of total makespans before and after introducing balanced operator
图 8 引入均衡算子前后集装箱数量对比
Figure 8. Comparison of numbers of container before and after introducing balanced operator
图 9 不同集装箱和集卡数量下的作业完成总时间
Figure 9. Total makespans under different numbers of containers and ITs
-
[1] 姚瑶. 港站铁水联运集装箱装卸搬运设备配置合理量研究[D]. 成都: 西南交通大学, 2012.YAO Yao. Studies on rational quantity configuration of handling equipment in container port by rail-water intermodal transport[D]. Chengdu: Southwest Jiaotong University, 2012. (in Chinese). [2] 刘勇, 朱晓宁, 朱颂雅, 等. 铁水联运港站的铁路作业区轨道门吊优化配置[J]. 武汉理工大学学报: 交通科学与工程版, 2014, 38 (5): 1135-1139. doi: 10.3963/j.issn.2095-3844.2014.05.042LIU Yong, ZHU Xiao-ning, ZHU Song-ya, et al. Allocation optimization model of the rail-mounted gantry crane in railway area by rail-water intermodal container transport[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2014, 38 (5): 1135-1139. (in Chinese). doi: 10.3963/j.issn.2095-3844.2014.05.042 [3] 武慧荣. 集装箱港口"船舶-堆场-列车"作业资源的调度优化[D]. 北京: 北京交通大学, 2015.WU Hui-rong. Handling resources scheduling optimization of"ships, yard, trains"container port[D]. Beijing: Beijing Jiaotong University, 2015. (in Chinese). [4] 冯力源. 集装箱港口铁水联运车船直取模式下的作业设备调度优化[D]. 北京: 北京交通大学, 2016.FENG Li-yuan. Scheduling optimization of handling equipment based on travel straight mode in container port by rail-water intermodal transport[D]. Beijing: Beijing Jiaotong University, 2016. (in Chinese). [5] 常祎妹, 朱晓宁, 闫柏丞, 等. 集装箱码头铁水联运装卸设备协同调度[J]. 交通运输系统工程与信息, 2017, 17 (4): 40-47. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201704007.htmCHANG Yi-mei, ZHU Xiao-ning, YAN Bai-cheng, et al. Integrated scheduling of handling operations in container terminal under rail-water intermodal transportation[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17 (4): 40-47. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201704007.htm [6] LEE D H, JIN Jian-gang, CHEN Jiang-hang. The integrated bay allocation and yard crane scheduling problem for transshipment containers[J]. Transportation Research Record, 2011 (2222): 63-71. [7] NIU Ben, XIE Ting, TAN Li-jing, et al. Swarm intelligence algorithms for yard truck scheduling and storage allocation problems[J]. Neurocomputing, 2016, 188: 284-293. doi: 10.1016/j.neucom.2014.12.125 [8] ZHEN Lu, YU Shu-cheng, WANG Shuai-an, et al. Scheduling quay cranes and yard trucks for unloading operations in container ports[J]. Annals of Operations Research, 2016, 247 (1): 1-24. doi: 10.1007/s10479-016-2305-2 [9] LUO Jia-bin, WU Yue, MENDES A B. Modelling of integrated vehicle scheduling and container storage problems in unloading process at an automated container terminal[J]. Computers and Industrial Engineering, 2016, 94: 32-44. doi: 10.1016/j.cie.2016.01.010 [10] LAU H Y K, ZHAO Ying. Integrated scheduling of handling equipment at automated container terminals[J]. International Journal of Production Economics, 2008, 112 (2): 665-682. doi: 10.1016/j.ijpe.2007.05.015 [11] LUO Jia-bin, WU Yue. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals[J]. Transportation Research Part E: Logistics and Transportation Review, 2015, 79: 49-64. doi: 10.1016/j.tre.2015.03.006 [12] XUE Zhao-jie, ZHANG Can-rong, MIAO Li-xin, et al. An ant colony algorithm for yard truck scheduling and yard location assignment problems with precedence constraints[J]. Journal of Systems Science and Systems Engineering, 2013, 22 (1): 21-37. doi: 10.1007/s11518-013-5210-0 [13] 周鹏飞. 面向不确定环境的集装箱码头优化调度研究[D]. 大连: 大连理工大学, 2005.ZHOU Peng-fei. Study on resource allocation under uncertainty environments in container terminal[D]. Dalian: Dalian University of Technology, 2005. (in Chinese). [14] CHEN Lu, XI Li-feng, CAI Jian-guo, et al. An integrated approach for modeling and solving the scheduling problem of container handling systems[J]. Journal of Zhejiang University: Science A, 2006, 7 (2): 234-239. doi: 10.1631/jzus.2006.A0234 [15] CHEN Lu, BOSTEL N, DEJAX P, et al. A tabu search algorithm for the integrated scheduling problem of container handling systems in a maritime terminal[J]. European Journal of Operational Research, 2007, 181 (1): 40-58. doi: 10.1016/j.ejor.2006.06.033 [16] ZENG Qing-cheng, YANG Zhong-zhen. Integrating simulation and optimization to schedule loading operations in container terminals[J]. Computers and Operations Research, 2009, 36 (6): 1935-1944. [17] MAK K L, ZHANG L. Simultaneous scheduling of import and export containers handling in container terminals[C]//International Association of Engineers. Proceedings of the World Congress on Engineering 2009. London: International Association of Engineers, 2009: 1-6. [18] 胡少龙, 胡志华. 集装箱港口桥吊、龙门吊和集卡集成调度的全自由度模型[J]. 武汉理工大学学报, 2012, 34 (5): 58-63. doi: 10.3963/j.issn.1671-4431.2012.05.013HU Shao-long, HU Zhi-hua. Full freedom optimization for integrated quay cranes, trucks and yard cranes in container port[J]. Journal of Wuhan University of Technology, 2012, 34 (5): 58-63. (in Chinese). doi: 10.3963/j.issn.1671-4431.2012.05.013 [19] 邢曦文. 基于混合流水作业组织的集装箱码头装卸集成调度优化[D]. 大连: 大连海事大学, 2013.XING Xi-wen. Optimization of container loading/unloading integrated scheduling in a container terminal based on hybrid flowshop[D]. Dalian: Dalian Maritime University, 2013. (in Chinese). [20] CHEN Lu, LANGEVIN A, LU Zhi-qiang. Integrated scheduling of crane handling and truck transportation in a maritime container terminal[J]. European Journal of Operational Research, 2013, 225 (1): 142-152. [21] LU Yi-qin, LE Mei-long. The integrated optimization of container terminal scheduling with uncertain factors[J]. Computers and Industrial Engineering, 2014, 75 (1): 209-216. [22] HE Jun-liang, HUANG You-fang, YAN Wei, et al. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption[J]. Expert Systems with Applications, 2015, 42 (5): 2464-2487. [23] KAVESHGAR N, HUYNH N. Integrated quay crane and yard truck scheduling for unloading inbound containers[J]. International Journal of Production Economics, 2015, 159 (3): 168-177. [24] HOMAYOUNI S M, TANG Sai-hong, MOTLAGH O. A genetic algorithm for optimization of integrated scheduling of cranes, vehicles, and storage platforms at automated container terminals[J]. Journal of Computational and Applied Mathematics, 2014, 270 (1): 545-556. [25] SKINNER B, YUAN Shuai, HUANG Shou-dong, et al. Optimisation for job scheduling at automated container terminals using genetic algorithm[J]. Computers and Industrial Engineering, 2013, 64 (1): 511-523. -
下载:
点击查看大图
图(9) / 表(6)
计量
- 文章访问数: 713
- HTML全文浏览量: 219
- PDF下载量: 365
- 被引次数: 0
