0.   引言

地铁具有运能大、准点率高等优点, 成为缓解城市交通拥堵的重要工具, 但市郊、市域线的乘客旅行时间依旧较长, 如上海地铁11号线, 全程旅行时间大于1.5h, 长距离线路的旅行速度依然有待提高。地铁车站间距小, 列车大多为站站停车模式, 停站是限制列车旅行速度的主要因素。在距离较长的地铁线路上, 为缩短长距离乘客的旅行时间, 提出了地铁快慢车运输组织模式, 优化地铁快慢车运行计划, 使长距离旅客旅行时间得以缩短, 同时保证线路运输组织的效率和成本, 成为亟需解决的问题。

目前, 在列车运行计划优化方面的研究较多, 范围较广。Niu等考虑动态客流需求, 建立了以乘客等待时间最小为目标的时刻表优化模型^{[1, 2]}; Yin等在考虑过载与不过载条件下, 建立了综合减少列车能耗和乘客等待时间的时刻表优化模型^{[3, 4]}; 唐海川等采用二次规划法优化列车追踪运行操纵序列, 提高再生制动能量的吸收利用来降低列车能耗^[5]; 胡文斌等采用粒子群算法调节列车停站时间, 优化列车时刻表以达到列车节能的目的^[6]; Huang等在Yin等的基础上, 建立了综合减少列车能耗和乘客等待时间的网络时刻表优化模型^[7]; Yang等考虑不同速度等级, 以列车运行时间最小为目标, 建立了时刻表优化的线性整数规划模型^[8]; Hassannayebi等考虑静态客流需求, 建立了以乘客等待时间最小为目标的网络时刻表优化模型^{[9, 10]}; Yue等建立了综合优化乘客等待时间和列车运输成本的列车停站方案优化模型, 并设计了相应的列生成启发式算法^[11]; Gao等考虑列车跳停、停运等策略, 提出了列车中断情况下的时刻表调整模型^{[12, 13]}; 李伟等考虑列车延误或客流拥挤情况下的运行计划调整问题, 并提出了相应的运行计划调整策略^{[14, 15]}; Jiang等考虑列车跳停、增开等策略, 提出了高峰客流拥挤条件下的时刻表优化模型, 并设计了相应的启发式算法^{[16, 17]}; Kang等考虑地铁末班车时刻表在换乘站的衔接问题, 建立了网络末班车换乘衔接优化模型及算法^{[18, 19, 20]}。

在地铁快慢车方面, 研究还相对较少。王智鹏等针对快慢车停站方案, 建立了基于车站分级的简约模型, 并设计模拟退火算法求解模型^[21]; 谭小土对快慢车模式下列车开行对数、停站方案分别进行了探讨^[22]; 王琳针对快慢车停站方案建立了双层优化模型^[23]; 张琛等以机场线为对象, 建立了仅考虑2种停站模式的快慢车停站方案优化模型^[24]; 陈晓峰以上海地铁16号线为例, 探讨了几种典型快慢车停站组合模式与开行比例^[25]。这些研究大都为对快慢车模式下的列车开行对数、停站方案与开行比例等进行了单独或分步优化, 但缺乏综合优化, 使得所编制的时刻表停站模式单一, 开行比例固定, 整体优化程度有限。

本文建立综合优化列车开行方案、停站方案和时刻表的地铁快慢车运行计划优化模型, 以满足客流需求为基础, 缩短乘客旅行时间与降低运营成本为双重目标, 综合优化列车运行计划。

1.   问题描述

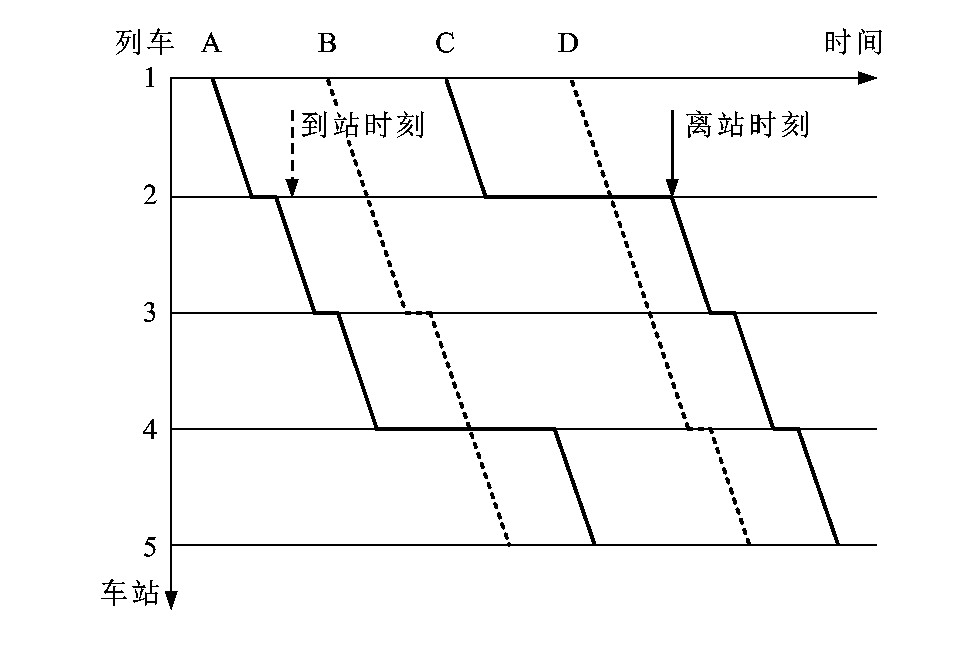
地铁快慢车运输组织指在保证大部分列车站站停车的基础上, 合理安排一定数量的跨站停列车, 以减少部分长距离乘客的旅行时间。其中站站停列车为慢车, 跨站停列车为快车。图 1中, 列车A、C站站停车, 为慢车, 列车B、D仅部分站停车, 为快车, 其中快车D在车站2越行慢车C。

图  1  快慢车示意

Figure  1.  Illustration of local/express trains

下载: 全尺寸图片 幻灯片

地铁快慢车运行计划的编制考虑因素多, 且问题规模较大, 为简化问题, 本文对部分复杂因素假设如下: 仅考虑一个方向的列车运行计划; 所有列车均由起点站发往终点站, 不考虑复杂交路运输组织模式; 只针对上、下客数量较为稳定的某一时段进行编制。

2.   数学建模

2.1   模型描述

2.1.1   初始时刻表

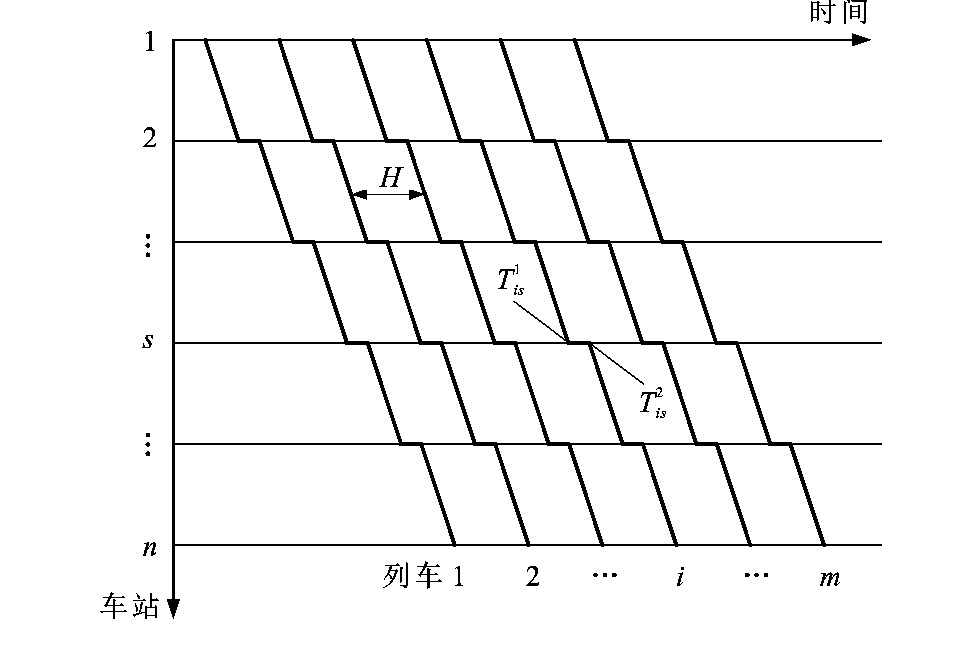
在模型初始阶段, 设定足够数量的列车, 列车的初始状态为等间隔站站停, 区间运行时间和停站时间均为最小允许值, 见图 2, 其中: H为列车间隔; m为列车数量; T_is¹、T_is²分别为列车i在车站s的初始到达与出发时刻; n为车站数量。

图  2  初始状态

Figure  2.  Initial condition

下载: 全尺寸图片 幻灯片

2.1.2   列车开行约束

初始状态设置的列车数量较多, 而实际列车开行数量只需满足客流需求即可, 因此, 在最优方案中, 会有部分列车被取消开行。引入变量b_i来表示列车i是否开行, 开行为1, 反之为0, 所有开行的列车集合形成最优开行方案。

当b_i取0时, 列车的到发时刻为在初始时刻基础上增加T_E, 此时其到发时刻在编制时段以外, 即认为被取消, 同时由于其时刻为初始时刻基础上加上T_E, 初始时刻表列车之间无任何冲突, 那么被取消的列车之间也不会相互干扰。为保证变量b_i能够取得正确的值, 需满足如下约束

式中: I为列车集合; S为车站集合; t_is¹、t_is²分别为列车i在车站s的到达与出发时刻; T_E为编制时段[0, T_E]的结束时刻。

2.1.3   始发时刻约束

在始发时刻约束保证任意列车i的始发时刻范围在初始时刻的一个发车间隔内, 具体约束为

式中: t_i1²为列车在始发站的发车时刻; T_i1²为列车在始发站的初始发车时刻。

2.1.4   停站约束

在快慢车模式下, 快车通过跨站停车来提高全程的旅行速度。引入变量d_is来表示列车i是否在车站s停车, 停车为1, 反之为0。为保证变量d_is能够取得正确的值, 同时保证列车停站时间在合理范围以内, 列车的到发时刻需满足如下约束

式中: D_s¹、D_s²分别为列车在车站s允许的最小和最大停站时间。

2.1.5   列车类型约束

地铁为城市公共交通, 需满足多样化的旅客出行需求, 因此, 开行快慢车仍需以站站停列车为主, 需对列车类型进行描述和识别。引入变量c_i来表示列车i是否为站站停列车, 站站停为1, 反之为0。为保证变量c_i取到正确值, 需满足如下约束

2.1.6   区间运行时间约束

由于列车运行计划是在计划层面编制, 且地铁列车均采用相同车型, 可认为列车在区间的运行速度是一样的。但在快慢车模式下, 列车有停站和不停站的区别, 需考虑列车加减速的启动和停站附加时间, 具体约束如下

式中: t₁、t₂分别为启动、停站附加时间; R_s^s+1为车站s与s+1之间的区间运行时间。

2.1.7   间隔约束

列车在实际运行过程中使用车站股道、区间股道须具备一定的间隔, 避免行车冲突。引入变量x_ijs表示列车i、j在车站s的发车顺序, 列车i在列车j之前发车为1, 反之为0;y_ijs表示列车i、j在车站s的到达顺序, 列车i在列车j之前到达为1, 反之为0;z_ijs表示列车i、j在车站s的发到顺序, 列车i在列车j到达之前出发为1, 反之为0。各间隔示意见图 3, 具体约束如下

式中: H₁为列车之间的最小到达间隔; H₂为最小的发车间隔; H₃为最小的发到间隔; M为无穷大正实数。

图  3  列车间隔

Figure  3.  Train headways

下载: 全尺寸图片 幻灯片

2.1.8   越行约束

区间一个方向仅有一条轨道, 列车在区间运行不得越行, 需满足如下约束

对于不具备越行条件的车站不得出现列车越行情况, 即对于任意列车j, 在其之前到达的列车与出发的列车数量相同, 满足如下约束

式中: G为排除越行站的车站集合。

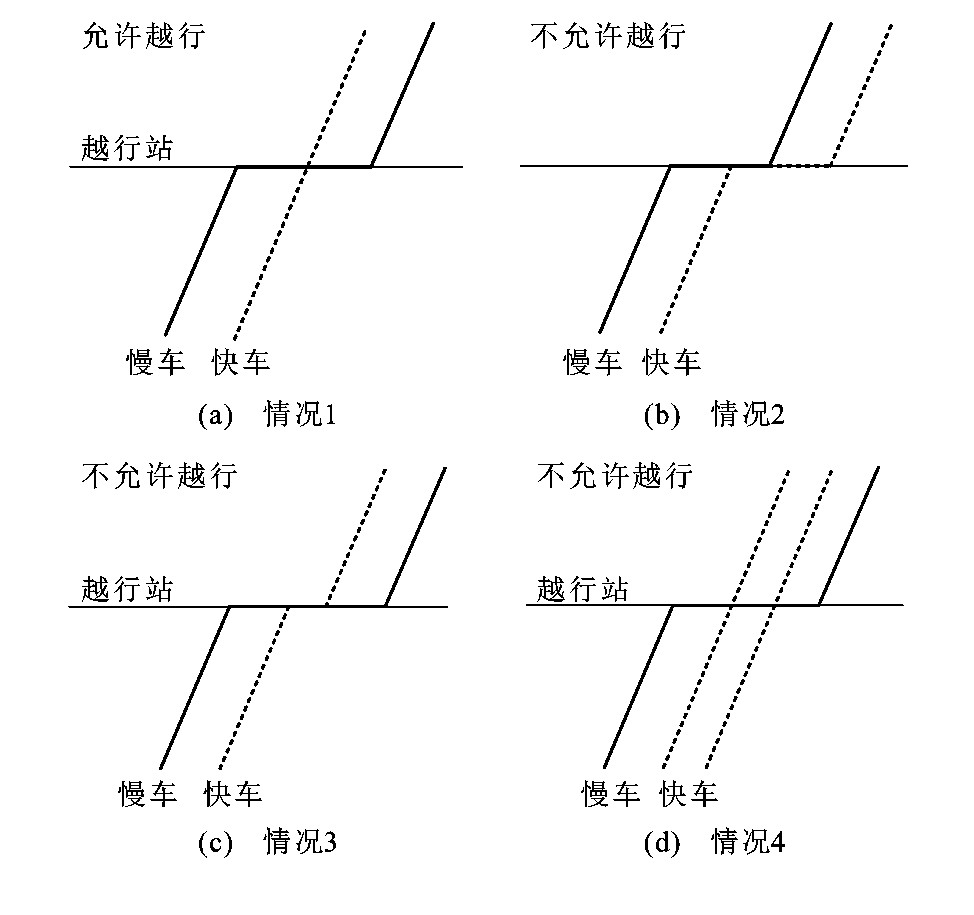
在允许越行的车站, 快车可能越行慢车, 但与铁路不同的是, 地铁在一个方向仅为一条股道设置站台供乘客上下车, 而越行股道不设置停站站台, 即要求越行列车在车站不得停站; 另外受地下空间限制, 地铁一般只设置一条越行股道, 见图 4, 情况1是唯一允许的情况, 其他3种情况均不允许, 因此, 需满足如下约束

式中: u_js为列车j到达车站s时, 车站的空闲股道数; S₀为越行站的集合。

对于越行站s: 当u_js≤1, 即列车j到达车站时, 最多只有一条空闲股道; 当u_js=1时, d_js必须为0, 即不停站; 当u_js=0时, d_js无限制。

图  4  不同越行情况

Figure  4.  Different overtaking instances

下载: 全尺寸图片 幻灯片

2.1.9   候车时间约束

地铁乘客出行类型多样, 过多开行快车, 会增加部分乘客的候车时间, 降低地铁的服务水平。图 5中, 乘客在虚线箭头处到达车站, 在实线箭头处离站, 间隔了2列快车, 等待时间较长。在快慢车模式下, 乘客乘车行为更复杂, 如部分乘客为选择乘坐快车而放弃乘坐下一班慢车。复杂的乘车行为使得准确计算乘客的候车时间极其困难, 为避免快慢车模式下乘客候车时间过长, 模型增加候车时间约束, 即要求乘客在任意时刻t进站, 在T_w时间内必须有站站停列车经过。

首先, 设λ_ist表示列车i在车站s是否在时刻t之后发车, 发车为1, 反之为0。为保证λ_ist取到正确的值, 设置如下约束

图  5  乘客候车时间

Figure  5.  Passenger waiting time

下载: 全尺寸图片 幻灯片

其次, 引入变量e_ist表示时刻t, 在T_w时间内, 是否存在站站停列车i经过车站s, 存在为1, 反之为0。为保证e_ist能够取到正确的值, 设置如下约束

最后, 为保证时刻t进站的乘客能够在T_w时间内乘上站站停列车, 需保证

2.1.10   客流需求约束

由于在编制时段内进站客流较为稳定, 此处引入参数δ_s¹和δ_s²分别表示车站s的平均上客量和下客量, 即对于每列停在车站s的列车, 其上客量均为δ_s¹, 下客量均为δ_s²。列车i在车站s能够载客, 必须保证列车开行且停站, 同时总上下车客流满足客流需求, 具体约束如下

式中: p_is为列车i能否在车站s载客, 能为1, 反之为0;Q_s¹为车站s的总进站客流; Q_s²为车站s的总出站客流。

2.1.11   目标函数

开行快慢车的目的是缩短乘客的旅行时间, 同时尽可能降低运输成本。乘客的旅行时间与其乘坐的列车直接相关, 乘坐快车则旅行时间短, 慢车则旅行时间较长, 而在快慢车模式下, 乘客选择列车的行为较为复杂, 因此, 难以精确计算所有乘客的旅行时间, 模型中采用缩短列车的旅行时间来近似代替。运输成本与开行列车数量直接相关, 模型采用列车开行数量来衡量运营成本, 因此, 目标函数W由两部分组成, 第1部分为列车的总旅行时间, 第2部分是开行的列车数量, 具体如下

式中: γ为目标函数两部分之间的权重系数。

2.2   复杂度分析

将本文所建立的地铁快慢车模型简称为ELT模型(Express/Local Train Model), 为混合整数规划模型, 其变量由线性变量和整数变量组成, 各变量规模由其所在集合的大小决定, 设q为编制时段内单位时刻数量, 问题复杂度分析具体见表 1: 以2h的编制范围为例, 时刻集合以min为单位(则q=120), 假设初始列车数量为30列, 车站数量为10个, 那么各约束规模如表 1中“实例数量”。可见, 涉及到时刻t的变量和约束数量较大, 其他则相对较小。

表  1  复杂度分析

Table  1.  Complexity analysis

下载: 导出CSV 

| 显示表格

2.3   两阶段近似算法

对模型进行整体优化计算, 其复杂度较高, 计算时间较长, 主要体现在候车约束的变量和约束条件较多。为提高求解效率, 本文设计两阶段近似算法, 设法简化候车约束。

2.3.1   第1阶段

近似确定慢车始发时刻, 具体方法如下。

Step 1:确定慢车的数量和始发时刻。慢车之间的间隔必须在T_w以内, 因此, 必须满足一定数量, 慢车数量N及其发车间隔H_L见式(20)、(21)。在首末班车时刻之间, 根据发车间隔均匀布设慢车, 并确定慢车始发时刻, 即

Step 2:在慢车始发时刻基础上, 调整其他列车始发时刻。图 6中, 实线箭头处为确定的慢车始发时刻, 将最接近的列车调整到相应时刻后, 再将慢车之间的列车进行等间隔调整, 形成调整后的初始时刻表。

图  6  初始时刻表调整

Figure  6.  Initial timetable adjustment

下载: 全尺寸图片 幻灯片

2.3.2   第2阶段

以确定的慢车集合与调整后的初始时刻表为输入, 同时保证相邻两列慢车在任意站的间隔小于T_w, 作为ELT模型的附加约束, 并去掉原有约束式(13) ~ (15), 形成新的ELT模型, 采用CPLEX求解器对ELT模型进行求解。

3.   实例验证

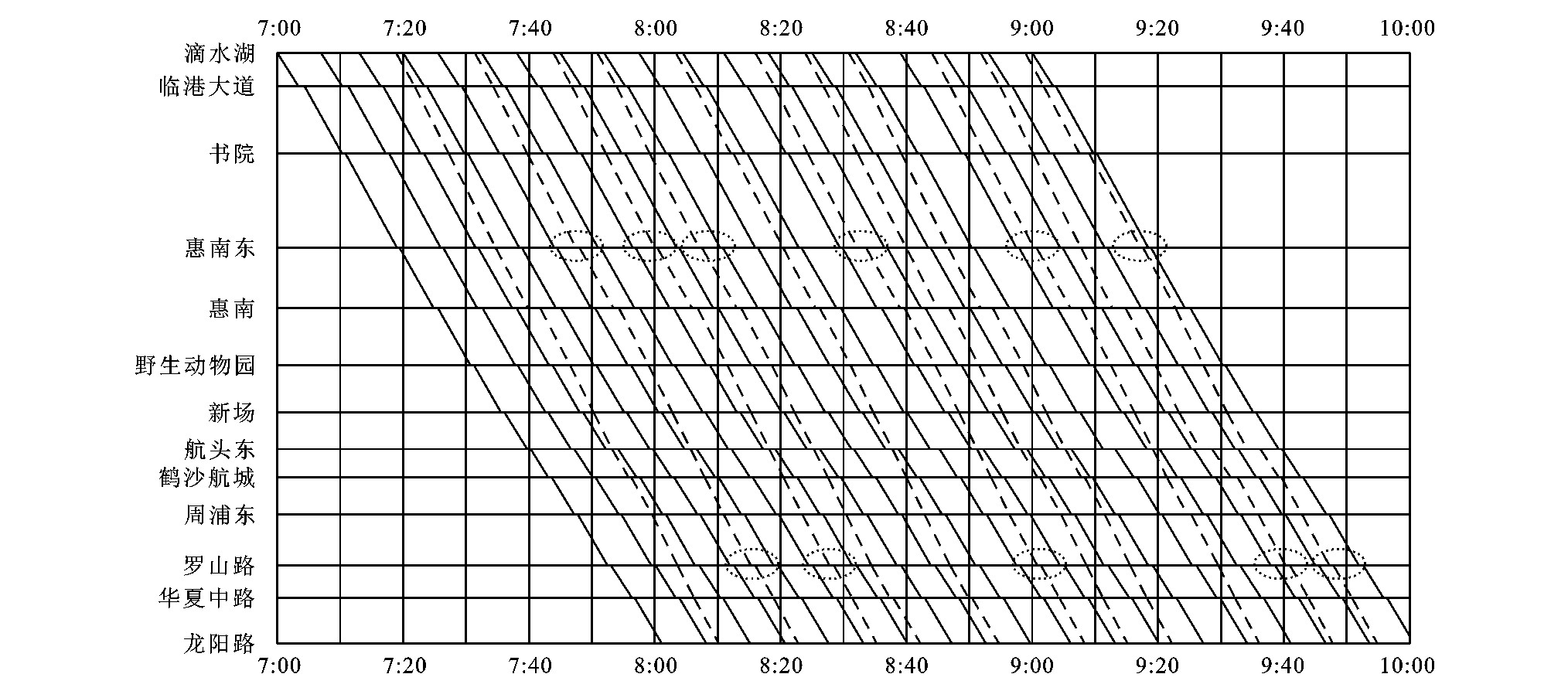
以上海地铁16号线实际数据为例, 来验证ELT模型的正确性和效率。上海地铁16号线是连接上海市中心龙阳路站到边远卫星城(临港新城) 滴水湖站的一条市郊线, 线路全长58.96km, 共设有13个车站, 见图 7, 其中在罗山路站、航头东站、野生动物园站、惠南东站和临港大道站设置有越行线, 根据现场运营测试情况, 仅航头东站、野生动物园站和惠南东站具备成熟的越行技术条件(双圆圈为越行站)。本文针对早高峰时段下行方向的快慢车运行计划编制, 对ELT模型进行测试, 以验证模型与两阶段近似算法的正确性与效率。

图  7  上海地铁16号线

Figure  7.  Shanghai Metro Line 16

下载: 全尺寸图片 幻灯片

3.1   基础数据

上海地铁16号线各车站停站时间约束与早高峰时段进出站客流见表 2。各车站平均上下客量与进出站客流、车厢拥挤情况、停站时间等多个因素有关, 需根据实际车站上客情况进行调查估算, 为降低试验难度, 在此对各车站平均上下客人数进行假设。

表  2  车站相关信息

Table  2.  Related informations of stations

下载: 导出CSV 

| 显示表格

H₁、H₂、H₃分别为60、60、40 s; 初始列车数量为31列; 列车发车间隔H为240 s; 首班车和末班车发车时刻分别为7:00和9:00;在各车站停站时间取最小停站时间; 乘客的最大忍耐候车时间T_w需对大量乘客进行调查后评估获得, 为降低试验难度, 此处假设为420 s; 目标函数中, 权重系数γ的取值需衡量列车旅行时间和列车开行数量之间的相互关系, 必须经过严格调研后评估获得, 为降低试验难度, 此处假设为5 000。

线路各区间距离和运行时间见表 3, 列车运行时间包括基础运行时间和附加运行时间(启动附加时间和停站附加时间)。

3.2   计算结果

采用两阶段近似算法进行求解, 设定求解终止条件为上下界相对间隔小于1%, 最长计算时间为600s, 经过137.68s的计算得出最优列车运行计划见图 8, 获取的上下界差距为0.85%, 目标函数值为258 390, 列车总旅行时间为104 750s。列车开行方案为: 列车开行30列, 包括快车11列, 慢车19列, 其中9列车在航头东站完成越行。停站方案中列车共完成87次跨站不停车, 其中快车全程最大节约时间628s, 节约近4.1%, 总节约旅行时间4 450s。可见ELT模型能够综合求解列车开行方案、列车停站方案与列车时刻表。此外, ELT模型具有以下特点。

表  3  区间相关信息

Table  3.  Related informations of interstations

下载: 导出CSV 

| 显示表格

(1) 列车停站方案较为灵活。ELT模型的停站方案不固定, 如惠南东站的进站量较大, 为4 430人, 而每次停车上客180人, 按需求需停站25次, 而慢车19列不能满足需求, ELT模型选择了6列快车在惠南东停站, 其他快车则不停站。罗山路站出站客流较大, 为5 814人, 而每次停车下客250人, 按需求需停站24次, 慢车无法满足需求, ELT模型选择了5列快车在惠南东停站, 其他快车则不停站, 见图 8中虚线框。

(2) 开行比例不固定。快慢车并非按照固定的比例开行, 而是根据客流需求灵活安排。

图  8  ELT模型求解结果

Figure  8.  Computing result of ELT model

下载: 全尺寸图片 幻灯片

3.3   不同列车规模的求解试验

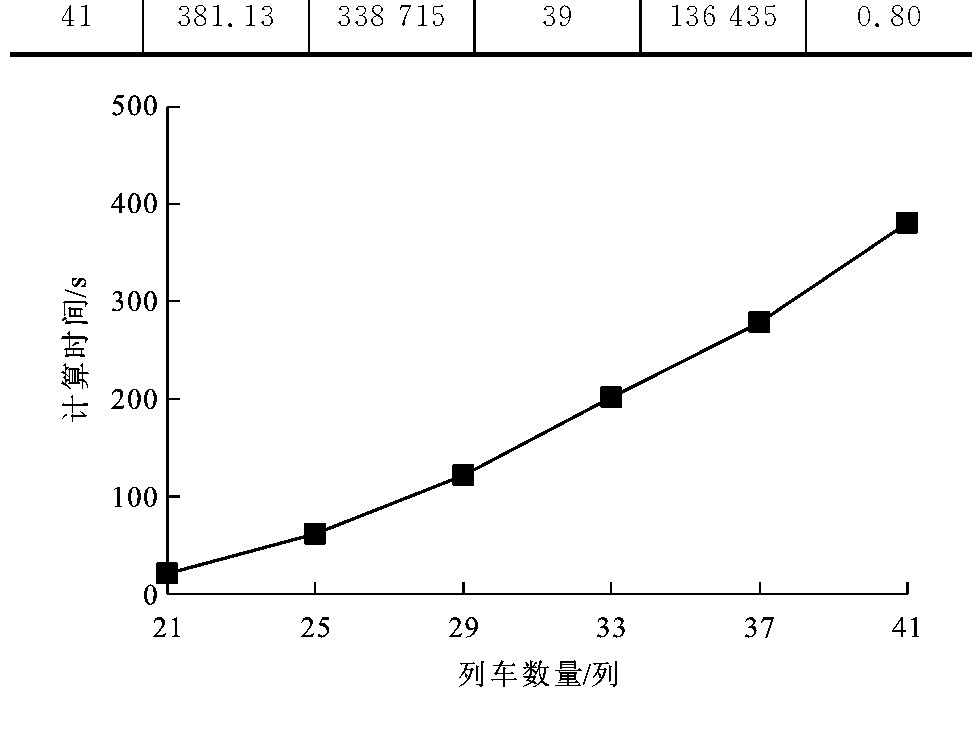
为分析不同计算规模下ELT模型与两阶段近似算法的效率, 分别设定不同规模初始列车数量, 测试其计算效率, 基本计算参数保持不变, 客流数据则根据列车数量, 进行相应的等比例改变, 计算结果见表 4, 可以看出: 在不同列车规模下, ELT模型均能够计算出相应快慢车运行计划, 但随着列车规模的增大, ELT模型及其两阶段近似算法的求解时间不断增长(增加趋势见图 9), 求解效率降低, 可见当规模增大到一定程度时, 有待进一步研究更加高效的求解算法。

表  4  测算结果

Table  4.  Testing result

下载: 导出CSV 

| 显示表格

图  9  不同列车数量下的计算时间

Figure  9.  Computing times under different train numbers

下载: 全尺寸图片 幻灯片

4.   结语

(1) 在严格构建快慢车运行的各项约束基础上, 设计了协调优化列车运行时间和运输成本的目标函数, 并完整构建出地铁快慢车运行计划综合优化模型(ELT模型); 所建立的ELT模型为混合整数规划模型, 模型变量与约束较多, 为提高求解效率, 设计了快速求解的两阶段近似算法。

(2) 以上海地铁16号线为例进行实例验证, 发现ELT模型及其两阶段近似算法能够快速求解快慢车运行计划, 所求解方案包含列车开行方案、列车停站方案和列车时刻表, 是一项综合优化模型, 并且具有更好的灵活性。

(3) ELT模型求解规模较大, 因此, 在很多因素上做了简化, 如候车时间方面, 仅在约束中限制候车时间不得过长, 并没有以优化乘客的候车时间为目标; 在客流约束方面, 仅考虑进出站客流, 没有直接考虑OD客流。优化候车时间、考虑OD客流, 并建立更加全面的快慢车运行计划优化模型是下一步需要研究的重点。