实测车流作用下大跨桥梁荷载效应极值外推法

鲁乃唯; 刘扬; 肖新辉

doi:10.19818/j.cnki.1671-1637.2018.05.005

实测车流作用下大跨桥梁荷载效应极值外推法

doi: 10.19818/j.cnki.1671-1637.2018.05.005

鲁乃唯^{1, 2,},
刘扬¹,
肖新辉³

1.
长沙理工大学土木工程学院, 湖南长沙 410114
2.
汉诺威莱布尼茨大学风险与可靠度研究所, 下萨克森汉诺威 30167
3.
长沙理工大学桥梁结构安全控制湖南省工程实验室, 湖南长沙 410114

基金项目:

国家重点基础研究发展计划项目 2015CB057705

国家自然科学基金项目 51378081

国家自然科学基金项目 51878072

湖南省自然科学基金项目 2018JJ3540

桥梁结构安全控制湖南省工程实验室开放基金项目 18KD02

详细信息

作者简介:
鲁乃唯(1987-), 男, 河南扶沟人, 长沙理工大学讲师, 工学博士, 从事桥梁结构可靠性与安全控制研究

中图分类号: U441.2
计量
- 文章访问数: 721
- HTML全文浏览量: 166
- PDF下载量: 352
- 被引次数: 0
出版历程
- 收稿日期: 2018-05-20
- 刊出日期: 2018-10-25

Extrapolating method of extreme load effects on long-span bridge under actual traffic loads

1.
School of Civil Engineering, Changsha University of Science and Technology, Changsha 410114, Hunan, China
2.
Institute for Risk and Reliability, Leibniz University Hannover, Lower Saxony, Germany
3.
Hunan Province Engineering Laboratory of Bridge Structure, Changsha University of Science and Technology, Changsha 410114, Hunan, China

More Information

Author Bio:
LU Nai-wei(1987-), male, lecturer, PhD, lunaiweide@163.com

摘要

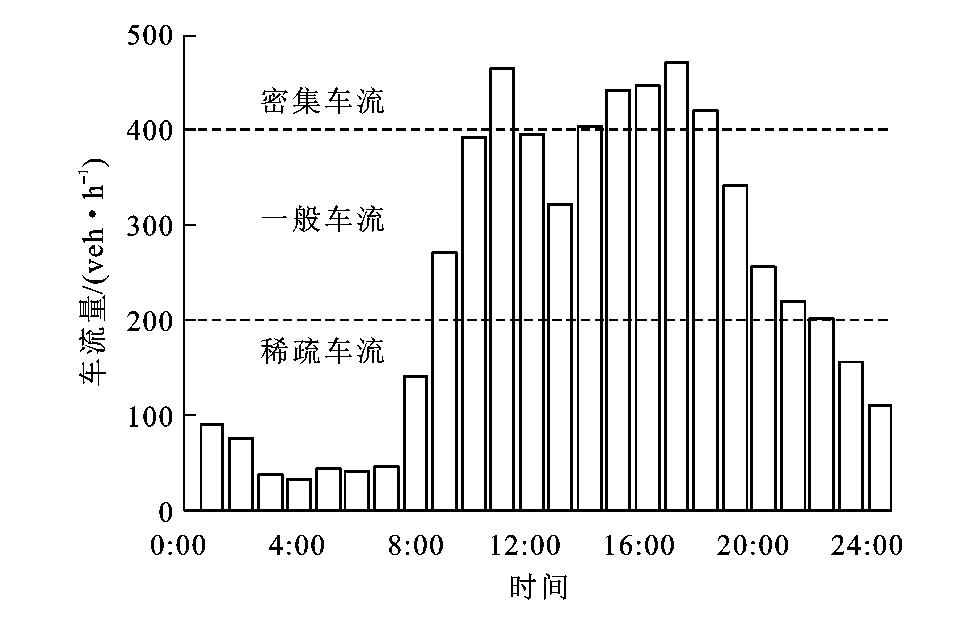
摘要: 提出多种密度随机车流作用效应极值的概率叠加方法, 外推了公路实测车流作用下大跨桥梁的车载效应极值; 阐述了基于Rice公式的界限跨阈率叠加原理, 并验证了其正确性; 基于中国某高速公路长期监测车流数据模拟了稀疏、一般和密集3种状态的随机车流, 应用界限跨阈率叠加模型估算了某混凝土斜拉桥主梁的最大弯矩。研究结果表明: 根据某高速公路实测车流数据, 稀疏、一般、密集车流密度分别约为1.7、5.0、8.3veh·min-1;在数值算例中, 车辆质量为45t车型占有率由0增加至80%导致最大车辆质量仅下降1.2%, 而车辆质量为50t的车型占有率由0增加到20%导致最大车辆质量增加14.4%, 说明多个平稳随机过程组合而成的非平稳随机过程的极值主要是由数值较大的随机过程决定; 采用跨阈率叠加方法对某混合车流车辆最大质量的外推误差为2.55%, 验证了将实际混合车流数据进行“车流离散”和“极值概率叠加”后得到的车载效应极值的方法的可行性; 密集车流占有率从0逐渐增加至5%导致斜拉桥主梁弯矩极值增幅为33.45%;某斜拉桥设计年限内的年均交通量增长率为2.8%, 对应的主梁跨中正弯矩极值超越设计标准值的概率为0.83, 高于设计要求, 需对桥梁车流量采取管控措施。
- 桥梁工程 /
- 车辆荷载 /
- 荷载效应极值 /
- 随机车流 /
- 动态称重 /
- 外推法
Abstract: A probabilistic superposition approach was proposed for investigating the extreme load effects of stochastic traffic flows with multiple densities.The approach was utilized to extrapolate the extreme values of vehicle load effects on the long-span bridges using the measured traffic data.The principle of superposing level-crossing rate based on the Rice's formula was explained, and its validity was proved.Three types of stochastic traffic flows, including the sparse flow, normal flow and dense flow, were simulated based on the long-term monitored traffic data of a highway bridge in China, and the maximum bending moment of a concrete cable-stayed bridge was analyzed based on the level-crossing superposition model.Analysis result shows that basedon the measured traffic data of a highway, the densities of free flow, normal flow and busy flow are 1.7, 5.0 and 8.3 veh·min-1, respectively.In the numerical example, when the occupancy of 45 t-vehicles increases from 0 to 80%, the maximum vehicle mass decreases by only 1.2%.But when the occupancy of 50 t-vehicles increases from 0 to 20%, the maximum vehicle mass decreases by 14.4%.This phenomenon indicates that the extreme value of a non-equilibrium random process composed by some stationary random processes is mostly depended on the random processes with higher values.The maximum extrapolating error of the maximum vehicle mass is2.55%for the mixed traffic flow using the level-crossing superposition approach, which explains that the extrapolating approach of extreme load effects on long-span bridges based on the principle of vehicle dispersion and superposition of extreme value probability is feasible.The increase of occupancy of dense traffic flow from 0 to 5%leads to an amplification of 33.45%for the maximum bending moment of the girder of a cable-stayed bridge.When the annual traffic growth rate of a cable-stayed bridge is 2.8%in the design lifetime, the probability that the midspan extreme bending moment of the bridge girder exceeds the design standard value is 0.83 and higher than the design requirements, therefore, it is deserved to take some measures to control the traffic flow.
- bridge engineering /
- vehicle load /
- extreme load effects /
- stochastic traffic flow /
- weigh-in-motion /
- extrapolation method

HTML全文

图 1 车流密度随时间变化趋势

Figure 1. Variation tendency of traffic density with time

下载: 全尺寸图片幻灯片

图 2 车距概率密度拟合曲线

Figure 2. Fitting curves of probability density of vehicle spaces

下载: 全尺寸图片幻灯片

图 3 车载效应极值分析流程

Figure 3. Extreme value analysis process of vehicular load effect

下载: 全尺寸图片幻灯片

图 4 Rice公式的基本原理

Figure 4. Basic principle of Rice's formula

下载: 全尺寸图片幻灯片

图 5 年跨阈率的拟合曲线

Figure 5. Fitting curves of annual level-crossing rate

下载: 全尺寸图片幻灯片

图 6 算例的数值分析结果

Figure 6. Numerical analysis results of example

下载: 全尺寸图片幻灯片

图 7 康博大桥桥型布置(单位: m)

Figure 7. Bridge layout of Kangbo Bridge (unit: m)

下载: 全尺寸图片幻灯片

图 8 关键节点的弯矩曲线

Figure 8. Bending moment curves of critical points

下载: 全尺寸图片幻灯片

图 9 关键节点密集车流下弯矩时程曲线

Figure 9. Time history curves of bending moments at critical points under dense flow

下载: 全尺寸图片幻灯片

图 10 跨阈率模拟结果

Figure 10. Simulated results of level-crossing rate

下载: 全尺寸图片幻灯片

图 11 不同车流占有率的界限跨阈率曲线

Figure 11. Level-crossing rate curves of traffic flows with different propotions

下载: 全尺寸图片幻灯片

图 12 随机车流作用下弯矩外推值

Figure 12. Extrapolated values of bending moments under random traffic flows

下载: 全尺寸图片幻灯片

图 13 车流比例对最大弯矩的影响曲线

Figure 13. Influence curves of traffic flow proportion on maximum bending moment

下载: 全尺寸图片幻灯片

图 14 弯矩超出设计荷载效应的失效概率

Figure 14. Failure probabilities of bending moment passing design load effect

下载: 全尺寸图片幻灯片

表 1 不同车型比例的跨阈率拟合参数与外推值

Table 1. Fitting parameters of level-crossing rates and extrapolated values considering different proportions of vehicle types

下载: 导出CSV

表 2 跨阈率拟合参数

Table 2. Fitting parameters of level-crossing rate

下载: 导出CSV

参考文献(30)

[1]	黄平明, 袁阳光, 赵建峰, 等. 重载交通下空心板桥梁承载能力安全性[J]. 交通运输工程学报, 2017, 17 (3): 1-12. doi: 10.3969/j.issn.1671-1637.2017.03.001 HUANG Ping-ming, YUAN Yang-guang, ZHAO Jian-feng, et al. Bearing capacity safety of hollow slab bridge under heavy traffic load[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (3): 1-12. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.03.001
[2]	鲁乃唯, 刘扬, NOORI M. 交通量持续增长下大跨桥梁时变极值外推分析[J]. 工程力学, 2018, 35 (7): 159-166. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201807018.htm LU Nai-wei, LIU Yang, NOORI M. Extrapolation of timevariant extreme effect on long-span bridge considering steadily growing traffic volume[J]. Engineering Mechanics, 2018, 35 (7): 159-166. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201807018.htm
[3]	DENG Lu, WANG Wei, YU Yang. State-of-the-art review on the causes and mechanisms of bridge collapse[J]. Journal of Performance of Constructed Facilities, 2016, 30 (2): 04015005-1-13. doi: 10.1061/(ASCE)CF.1943-5509.0000731
[4]	NOWAK A S. Load model for bridge design code[J]. Canadian Journal of Civil Engineering, 1994, 21 (1): 36-49. doi: 10.1139/l94-004
[5]	CAPRANIC C. Calibration of a congestion load model for highway bridges using traffic microsimulation[J]. Structural Engineering International: Journal of the International Association for Bridge and Structural Engineering, 2012, 22 (3): 342-348.
[6]	LU Nai-wei, BEER M, NOORI M, et al. Lifetime deflections of long-span bridges under dynamic and growing traffic loads[J]. Journal of Bridge Engineering, 2017, 22 (11): 04017086-1-12. doi: 10.1061/(ASCE)BE.1943-5592.0001125
[7]	韩万水, 闫君媛, 武隽, 等. 基于长期监测的特重车交通荷载特性及动态过桥分析[J]. 中国公路学报, 2014, 27 (2): 54-61. doi: 10.3969/j.issn.1001-7372.2014.02.007 HAN Wan-shui, YAN Jun-yuan, WU Jun, et al. Extraheavy truck load features and bridge dynamic response based on long-term traffic monitoring record[J]. China Journal of Highway and Transport, 2014, 27 (2): 54-61. (in Chinese). doi: 10.3969/j.issn.1001-7372.2014.02.007
[8]	祝志文, 黄炎, 向泽. 货运繁重公路的车辆荷载谱和疲劳车辆模型[J]. 交通运输工程学报, 2017, 17 (3): 13-24. doi: 10.3969/j.issn.1671-1637.2017.03.002 ZHU Zhi-wen, HUANG Yan, XIANG Ze. Vehicle loading spectrum and fatigue truck models of heavy cargo highway[J]. Journal of Traffic and Transportation Engineering, 2017, 17 (3): 13-24. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.03.002
[9]	OBRIEN E J, ENRIGHT B. Modeling same-direction twolane traffic for bridge loading[J]. Structural Safety, 2011, 33 (4/5): 296-304.
[10]	O'CONNOR A, OBRIEN E J. Traffic load modelling and factors influencing the accuracy of predicted extremes[J]. Canadian Journal of Civil Engineering, 2005, 32 (1): 270-278. doi: 10.1139/l04-092
[11]	CAPRANI C C, OBRIEN E J, LIPARI A. Long-span bridge traffic loading based on multi-lane traffic micro-simulation[J]. Engineering Structures, 2016, 115: 207-219. doi: 10.1016/j.engstruct.2016.01.045
[12]	OBRIEN E J, ENRIGHT B. Using weigh-in-motion data to determine aggressiveness of traffic for bridge loading[J]. Journal of Bridge Engineering, 2013, 18 (3): 232-239. doi: 10.1061/(ASCE)BE.1943-5592.0000368
[13]	OBRIEN E J, LIPARI A, CAPRANI C C. Micro-simulation of single-lane traffic to identify critical loading conditions for long-span bridges[J]. Engineering Structures, 2015, 94: 137-148. doi: 10.1016/j.engstruct.2015.02.019
[14]	MIAO T J, CHAN T H T. Bridge live load models from WIM data[J]. Engineering Structures, 2002, 24 (8): 1071-1084. doi: 10.1016/S0141-0296(02)00034-2
[15]	阮欣, 周小燚, 郭济. 基于合成车流的桥梁车辆荷载效应极值预测[J]. 同济大学学报: 自然科学版, 2012, 40 (10): 1458-1462, 1485. doi: 10.3969/j.issn.0253-374x.2012.10.004 RUAN Xin, ZHOU Xiao-yi, GUO Ji. Extreme value extrapolation for bridge vehicle load effect based on synthetic vehicle flow[J]. Journal of Tongji University: Natural Science, 2012, 40 (10): 1458-1462, 1485. (in Chinese). doi: 10.3969/j.issn.0253-374x.2012.10.004
[16]	阮欣, 周军勇, 石雪飞. 桥梁汽车荷载响应的极值外推方法综述[J]. 同济大学学报: 自然科学版, 2015, 43 (9): 1339-1346. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201509009.htm RUAN Xin, ZHOU Jun-yong, SHI Xue-fei. Review on extreme extrapolation methods for bridge traffic load response[J]. Journal of Tongji University: Natural Science, 2015, 43 (9): 1339-1346. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201509009.htm
[17]	李植淮, 李春前, 孙健康, 等. 基于GPD模型的车辆荷载效应极值估计[J]. 工程力学, 2012, 29 (增1): 166-171. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2012S1035.htm LI Zhi-Huai, LI Chun-qian, SUN Jian-kang, et al. Estimation of extreme vehicle load effect based on GPD model[J]. Engineering Mechanics, 2012, 29 (S1): 166-171. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2012S1035.htm
[18]	冯海月, 伊廷华, 陈斌. 采用广义Pareto分布进行车辆荷载效应极值估计的研究[J]. 振动与冲击, 2015, 34 (15): 7-11, 22. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201515003.htm FENG Hai-yue, YI Ting-hua, CHEN Bin. Extreme estimation for vehicle load effect based on generalized Pareto distribution[J]. Journal of Vibration and Shock, 2015, 34 (15): 7-11, 22. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201515003.htm
[19]	刘浪, 尤吉. 公路桥梁车辆荷载效应的外推计算[J]. 土木工程学报, 2015, 48 (4): 59-64. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201504011.htm LIU Lang, YOU Ji. Extrapolation method for truck load effects on highway bridges[J]. China Civil Engineering Journal, 2015, 48 (4): 59-64. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201504011.htm
[20]	宗周红, 杨泽刚, 夏叶飞, 等. 拥堵运行状态下新沂河大桥车辆荷载模型[J]. 中国公路学报, 2016, 29 (2): 44-51. doi: 10.3969/j.issn.1001-7372.2016.02.006 ZONG Zhou-hong, YANG Ze-gang, XIA Ye-fei, et al. Vehicle load model for Xinyihe River Bridge under congested running status[J]. China Journal of Highway and Transport, 2016, 29 (2): 44-51. (in Chinese). doi: 10.3969/j.issn.1001-7372.2016.02.006
[21]	夏樟华, 陈俊民, 宗周红, 等. 并道运行状态下高速公路桥梁车辆荷载效应[J]. 长安大学学报: 自然科学版, 2017, 37 (1): 76-84. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201701010.htm XIA Zhang-hua, CHEN Jun-min, ZONG Zhou-hong, et al. Vehicle load effect of expressway bridge in the state of lanes merging[J]. Journal of Chang'an University: Natural Science Edition, 2017, 37 (1): 76-84. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL201701010.htm
[22]	周军勇, 石雪飞, 阮欣, 等. 高速公路分车道荷载差异及其响应特性[J]. 同济大学学报: 自然科学版, 2018, 46 (4): 458-464. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201804007.htm ZHOU Jun-yong, SHI Xue-fei, RUAN Xin, et al. Lane load disparities and their loading effect characteristics of freeway[J]. Journal of Tongji University: Natural Science, 2018, 46 (4): 458-464. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201804007.htm
[23]	CHEN S R, WU J. Modeling stochastic live load for longspan bridge based on microscopic traffic flow simulation[J]. Computers and Structures, 2011, 89 (9/10): 813-824.
[24]	OBRIEN E J, HAYRAPETOVA A, WALSH C. The use of micro-simulation for congested traffic load modeling of mediumand long-span bridges[J]. Structure and Infrastructure Engineering, 2012, 8 (3): 269-276.
[25]	韩大章, 周军勇, 朱荣, 等. 基于计重收费数据的大跨径桥梁荷载效应评估[J]. 桥梁建设, 2018, 48 (4): 27-32. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201804006.htm HAN Da-zhang, ZHOU Jun-yong, ZHU Rong, et al. Assessment of traffic load effects of long-span bridge based on toll-by-weight data[J]. Bridge Construction, 2018, 48 (4): 27-32. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201804006.htm
[26]	刘扬, 鲁乃唯, 邓扬. 基于实测车流的钢桥面板疲劳可靠度评估[J]. 中国公路学报, 2016, 29 (5): 58-66. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201605009.htm LIU Yang, LU Nai-wei, DENG Yang. Fatigue reliability assessment of steel bridge decks under measured traffic flow[J]. China Journal of Highway and Transport, 2016, 29 (5): 58-66. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201605009.htm
[27]	CREMONA C. Optimal extrapolation of traffic load effects[J]. Structural Safety, 2001, 23 (1): 31-46.
[28]	鲁乃唯, 罗媛, 汪勤用, 等. 车载下大跨度桥梁动力可靠度评估[J]. 浙江大学学报: 工学版, 2016, 50 (12): 2328-2335. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201612012.htm LU Nai-wei, LUO Yuan, WANG Qin-yong, et al. Dynamic reliability assessment for long-span bridges under vehicle load[J]. Journal of Zhejiang University: Engineering Science, 2016, 50 (12): 2328-2335. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201612012.htm
[29]	OBRIEN E J, BORDALLO-RUIZ A, ENRIGHT B. Lifetime maximum load effects on short-span bridges subject to growing traffic volumes[J]. Structural Safety, 2014, 50: 113-122.
[30]	鲁乃唯. 随机车流下悬索桥加劲梁动力响应概率模型与可靠度研究[D]. 长沙: 长沙理工大学, 2014. LU Nai-wei. Probability model of dynamic responses and reliability assessment for stiffening girders of suspension bridges under random traffic flow[D]. Changsha: Changsha University of Science and Technology, 2014. (in Chinese).