0.   引言

航海模拟器已经广泛地应用于航海教育、培训与相关科学研究中。航海模拟器的性能主要由行为真实感、物理真实感和操作环境真实感等决定^[1]。行为真实感主要取决于船舶运动数学模型的可靠性与精准性。目前, 中国航海模拟器中的船舶运动数学模型很大一部分依赖于进口, 这极大地影响了中国航海模拟器的自主性与竞争力, 因此, 建立可靠、精确与实用的船舶运动数学模型具有重要意义。

船舶航行在海洋中, 时时刻刻遭受波浪的作用, 如何有效地预报船舶在波浪中每时每刻的运动姿态对航海模拟器的行为真实感具有极大意义。钱小斌等基于Froude-Krylov假设, 建立了船舶在规则波浪中的运动数学模型和受力模型^[2], 但将船舶假定为箱体, 极大地限制了船舶运动模型的适用范围; 侯圣贤在二维频域理论范畴内基于普通切片法对田才图谱进行插值, 从而求得了船舶水动力系数, 并建立了船舶迎浪垂荡纵摇运动数学模型^[3], 但田才图谱只适用于特定船型和频率, 极大地限制了其应用范围, 且在插值调用田才图谱时也容易产生较大误差; Salvensen等基于切片法在二维频域内建立了船舶在规则波浪中的线性运动模型, 预报结果与实船运动吻合良好^[4], 但由于切片法固有的理论局限性, 只能应用于细长体(忽略船体三维几何特征) 在特定频率和航速下的运动预报, 且其对船体表面压力和随波浪下的运动预报存在不可忽视的误差。计算机性能的快速提高使得基于三维频域理论预报船舶在波浪中的运动取得了极大成果。洪亮等对有航速三维频域Green函数进行了精确数值计算, 并进一步分析了不同航速下三维移动脉动源的波形, 为三维频域内船舶水动力分析和运动预报奠定了基础^[5]; 邹元杰等基于高频低速假定对零航速Green函数进行了航速修正, 并计算了船舶在波浪中低速行驶时所受的压力^[6]; Guevel等基于三维频域Green函数法, 对有航速船舶的绕射与辐射问题进行了水动力分析^[7]; 周正全等采用低航速理论对船舶在波浪中的相对运动进行了数值计算, 与切片法和零航速Green函数法相比, 其数值预报精度有较大提高^[8]。总体来说, 三维频域理论虽然在一定程度上解决了二维切片理论适用范围不广的缺陷, 但有航速频域Green函数计算耗时且复杂, 水线积分项数值处理极其困难, 对高航速下的船舶运动预报造成了严重的误差。此外, 三维频域理论不能解决船舶操纵等瞬态问题。在三维时域范畴下, Liapis等基于三维时域Green函数法建立了船舶在静水中的水动力分析与运动模型^{[9, 10]}; King等进一步建立了船舶在波浪中的三维时域运动模型, 精确地求解出船舶以任意航速在规则波浪中的摇荡运动, 也为甲板上浪、螺旋桨出水和舰载机着舰等其他航海情景的仿真奠定了基础^{[11, 12, 13, 14, 15, 16]}。三维时域Green函数精确计算是准确预报船舶三维时域运动的关键。Liapis等采用小时间区域级数展开和大时间区域渐进式算法对三维时域Green函数进行了数值计算^{[9, 11, 17]}, 但其直接计算耗时较长, 且大、小时间区域划分不明确; 黄德波采用节点制表和节点间插值方法求解三维时域Green函数, 极大地缩短了三维时域Green函数的数值求解时间^[18], 但由于三维时域Green函数中的被积分函数是高频振荡函数, 在大时间区域制表中节点不够密的情况下进行插值会带来较大误差; Chuang等基于Taylor级数展开求解满足三维时域Green函数的常微分方程^{[19, 20, 21, 22]}, 但当场点与源点都接近或位于自由液面时, 三维时域Green函数振荡增幅尤为剧烈, 且Taylor展开项数较难选择与判断; Li等采用精细时程积分法求解满足三维时域Green函数的常微分方程, 在大时间区域内避免了采用4阶Runge-Kutta法制表带来的三维时域Green函数发散问题^{[23, 24, 25, 26]}, 但由于其将计算域划分得过于精细, 且求解常微分方程过程中所形成的系数矩阵阶数较高, 导致其制表耗时过长。

针对现有航海模拟器中船舶运动数学模型建模方法的不足, 本文基于三维时域理论建立船舶在规则波浪中的运动数学模型, 将三维时域Green函数划分为3个时间区域^[27], 在小时间区域采用级数展开法, 在中间过渡时间区域采用精细积分法, 在大时间区域采用渐进展开法, 并对三维时域Green函数进行数值计算; 将三维时域Green函数分为振荡较为激烈的解析解部分与振荡较为平缓的数值解部分, 并对平缓数值解部分进行节点制表以便插值调用; 以Wigley Ⅰ型船舶与S60型船舶为仿真对象, 对比数值计算结果和试验结果, 以验证在规则波浪中建立的船舶运动数学模型的精准性与可靠性。

1.   船舶在规则波浪中的运动数学模型

1.1   建立坐标系

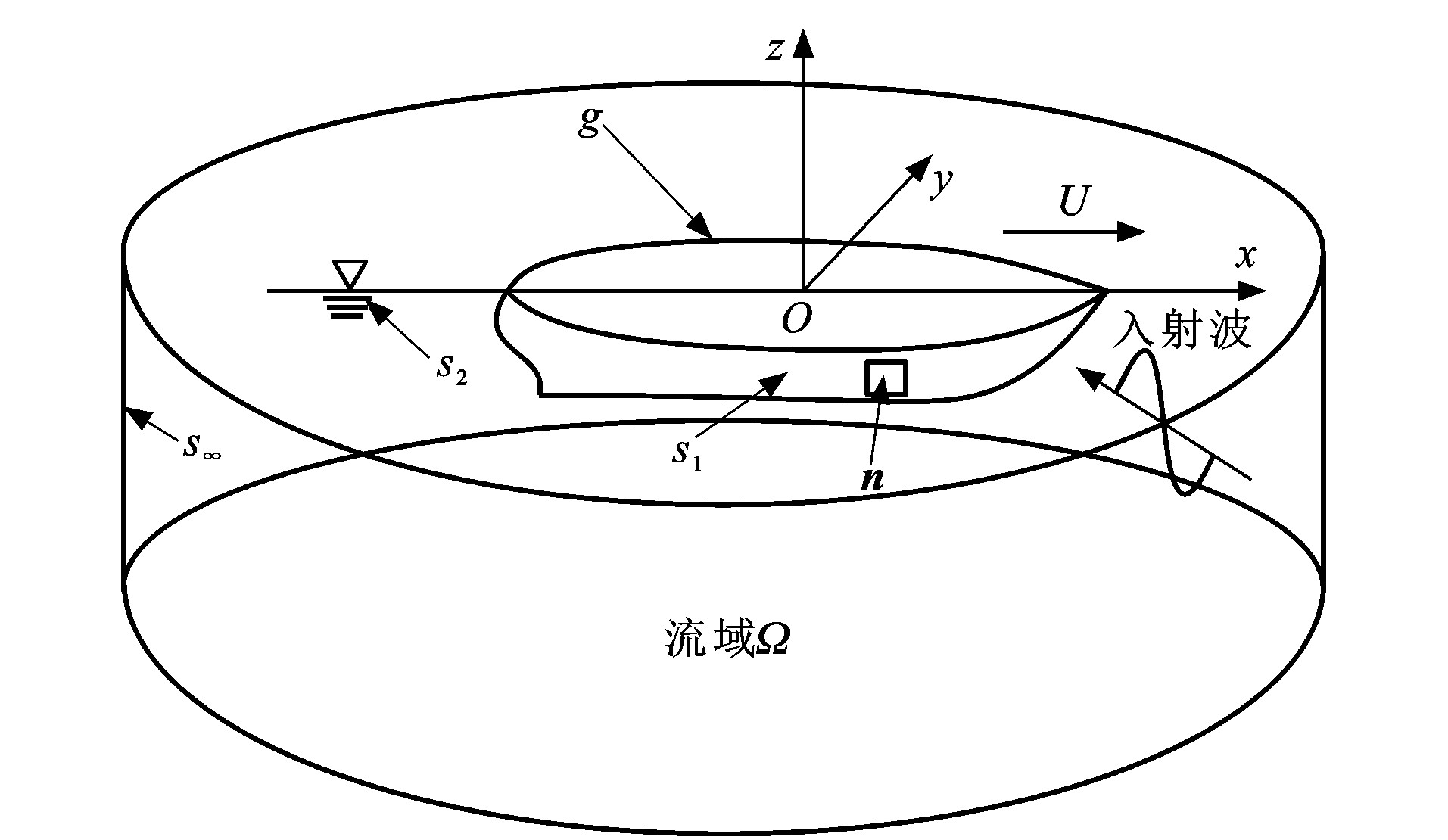
为便于研究船舶在波浪中的运动情况, 采用随船运动坐标系, 见图 1, 参考坐标系Oxyz随船舶以定常且平行于x轴的航速U移动, xOy面与静水面(z=0) 重合, z轴垂直向上; 流域Ω由船体平均湿表面S₁、线性自由液面S₂和无穷远处控制面S_∞围成; n为单位法线矢量, 指向船体内部; S₁与S₂的交线为γ, 以逆时针方向为正方向。

图  1  坐标系与流域定义

Figure  1.  Definitions of coordinate system and fluid domain

下载: 全尺寸图片 幻灯片

1.2   边界条件与初值条件

本文在势流理论的范畴内进行研究, 假定流体无黏性, 流动无旋且不可压缩, 在Oxyz参考坐标系下流场存在速度势Φ₁, 基于线性理论可以将速度势Φ₁分解为^[11]

$\begin{array}{l}\Phi {}_1=-Ux+\Phi {}_2(x,y,z,t)+\text{ϕ}{}_0(x,y,z,t)+\\ {\displaystyle \sum _{k=1}^7\text{ϕ}}{}_k(x,y,z,t)(1)\end{array}$

式中: Φ₂ (x, y, z, t) 为由定常速度产生的兴波速度势; ϕ₀ (x, y, z, t) 为入射波速度势; ϕ_k (x, y, z, t) 为不定常速度势, 其中ϕ₁ (x, y, z, t)、ϕ₂ (x, y, z, t)、…、ϕ₆ (x, y, z, t) 为辐射速度势, ϕ₇ (x, y, z, t) 为绕射速度势; t为当前时刻。

不定常速度势ϕ_k (x, y, z, t) 应满足如下条件。

(1) 在流域Ω中满足Laplace方程

$\nabla {}^2\text{ϕ}{}_k(x,y,z,t)=0(2)$

式中: ∇²为Laplace算子。

(2) 在线性自由液面S₂处应满足的条件为

$\begin{array}{l}\left(\frac{\partial }{\partial t}-U\frac{\partial }{\partial x}\right){}^2\text{ϕ}{}_k(x,y,z,t)+\\ g\frac{\partial \text{ϕ}{}_k(x,y,z,t)}{\partial z}=0(3)\end{array}$

式中: g为重力加速度。

(3) 在船体平均湿表面S₁处应满足的条件为

$\begin{array}{l}\frac{\partial \text{ϕ}{}_7(x,y,z,t)}{\partial \mathit{n}}=-\frac{\partial \text{ϕ}{}_0(x,y,z,t)}{\partial \mathit{n}}(4)\\ \frac{\partial \text{ϕ}{}_k(x,y,z,t)}{\partial \mathit{n}}=n{}_k\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(t)+m{}_k\zeta {}_k(t)(5)\end{array}$

式中: ζ_k (t) 为船舶k (k=1, 2, …, 6) 模态运动位移; n_k为广义法向量的k模态分量; m_k为恒定速度的k模态梯度。

由船体几何形状可得k模态的n_k和m_k分别为^[9]

$\begin{array}{l}\mathit{r}=(x,y,z)(6)\\ \mathit{n}=(n{}_1,n{}_2,n{}_3)(7)\\ \mathit{r}\times \mathit{n}=(n{}_4,n{}_5,n{}_6)(8)\\ (m{}_1,m{}_2,m{}_3)=(0,0,0)(9)\\ (m{}_4,m{}_5,m{}_6)=(0,Un{}_3,-Un{}_2)(10)\end{array}$

式中: r为船体平均湿表面上任意一点的位置矢量。

(4) 在无穷远处控制面S_∞处应满足的条件为

$\text{ϕ}{}_k(x,y,z,t),\nabla \text{ϕ}{}_k(x,y,z,t)\to 0(11)$

(5) 初始条件为

$\{\begin{array}{c}\text{ϕ}{}_k(x,y,z,t)=0\hfill \\ \partial \text{ϕ}{}_k(x,y,z,t)/\partial t=0\hfill \\ t{}_0=0k=1,2,\cdots ,6\hfill \\ t{}_0=-\infty k=7\hfill \end{array}(12)$

式中: t₀为初始时刻。

引入三维时域Green函数求解上述定解问题, 则无限水深三维时域Green函数G (x₁, y₁, z₁, x₂, y₂, z₂, t, τ) 为^[9]

式中: R₁为场点P (x₁, y₁, z₁) 到源点Q (x₂, y₂, z₂) 的距离; R₂为场点P与源点Q关于静水面镜像点的距离; R₃为场点P到源点Q的水平距离; τ为过去某一时刻; δ (·) 为Dirac函数; H (·) 为单位阶跃函数; J₀ (·) 为第1类0阶贝塞尔函数; K为波数; G₁ (x₁, y₁, z₁, x₂, y₂, z₂, t, τ) 为三维时域Green函数的波动部分; G₀ (x₁, y₁, z₁, x₂, y₂, z₂) 为三维时域Green函数的瞬时部分。

三维时域Green函数的瞬时部分G₀ (x₁, y₁, z₁, x₂, y₂, z₂) 在四边形平面面元积分可以用Hess-Smith方法^[28]计算。

不定常速度势ϕ_k (x₁, y₁, z₁, t) 的边界积分方程为^[11]

$\begin{array}{l}2\text{π}\text{ϕ}{}_k(x{}_1,y{}_1,z{}_1,t)+{\displaystyle \underset{S{}_1}{\iint }\text{ϕ}}{}_k(x{}_2,y{}_2,z{}_2,t)\frac{\partial G{}_0(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2)}{\partial \mathit{n}{}_Q}\text{d}S={\displaystyle \underset{S{}_1}{\iint }G}{}_0(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2)\cdot \\ \frac{\partial \text{ϕ}{}_k(x{}_2,y{}_2,z{}_2,t)}{\partial \mathit{n}{}_Q}\text{d}S+{\displaystyle \int }{}_{t{}_0}^t\text{d}\tau {\displaystyle \underset{S{}_1}{\iint }G}{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )\frac{\partial \text{ϕ}{}_k(x{}_2,y{}_2,z{}_2,\tau )}{\partial \mathit{n}{}_Q}\text{d}S-\\ {\displaystyle \int }{}_{t{}_0}^t\text{d}\tau {\displaystyle \underset{S{}_1}{\iint }\text{ϕ}}{}_k(x{}_2,y{}_2,z{}_2,\tau )\frac{\partial G{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )}{\partial \mathit{n}{}_Q}\text{d}S-\frac{U{}^2}{g}{\displaystyle \int }{}_{t{}_0}^t\text{d}\tau {\displaystyle \underset{\gamma }{\oint }}\text{ϕ}{}_k(x{}_2,y{}_2,z{}_2,\tau )\cdot \\ \frac{\partial G{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )}{\partial x{}_2}\text{d}y{}_2+\frac{U{}^2}{g}{\displaystyle \int }{}_{t{}_0}^t\text{d}\tau {\displaystyle \underset{\gamma }{\oint }}G{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )\frac{\partial \text{ϕ}{}_k(x{}_2,y{}_2,z{}_2,\tau )}{\partial x{}_2}\text{d}y{}_2+\\ \frac{2U}{g}{\displaystyle \int }{}_{t{}_0}^t\text{d}\tau {\displaystyle \underset{\gamma }{\oint }}\text{ϕ}{}_k(x{}_2,y{}_2,z{}_2,\tau )\frac{\partial G{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )}{\partial \tau }\text{d}y{}_2(19)\end{array}$

式中: S为积分面积变量; n_Q为源点Q处的单位法线矢量。

将船体平均湿表面离散为满足精度要求的一定数量的四边形平面面元, 并假定各个面元上的不定常速度势为常数(常数面元法), 建立线性方程组, 求解出每个面元上的不定常速度势。

1.3   辐射问题求解

应用脉冲响应方法, 则辐射速度势ϕ_k (x₁, y₁, z₁, t) (k=1, 2, …, 6) 可表示为^[9]

$\begin{array}{l}\text{ϕ}{}_k(x{}_1,y{}_1,z{}_1,t)={\displaystyle {\int }_0^t\phi }{}_k(x{}_1,y{}_1,z{}_1,\\ t-\tau )\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(\tau )\text{d}\tau (20)\end{array}$

式中: φ_k (x₁, y₁, z₁, t) 为辐射速度势ϕ_k (x₁, y₁, z₁, t) 的脉冲响应函数。

ϕ_k (x₁, y₁, z₁, t) 可由瞬时部分Ψ_1k (x₁, y₁, z₁) 和记忆部分Ψ_2k (x₁, y₁, z₁)、χ_k (x₁, y₁, z₁, t) 组成, 即

φ_k (x₁, y₁, z₁, t) =Ψ_1k (x₁, y₁, z₁) δ (t) +

Ψ_2k (x₁, y₁, z₁) H (t) +χ_k (x₁, y₁, z₁, t) (21)

将式(20)、(21) 代入式(19) 即可得到船体表面各个面元上的Ψ_1k (x₁, y₁, z₁)、Ψ_2k (x₁, y₁, z₁) 和χ_k (x₁, y₁, z₁, t)。则由k模态运动引起j模态辐射力和力矩F_jk (t) 可表示为

$\begin{array}{l}F{}_{jk}(t)=-a{}_{jk}\stackrel{\cdot \cdot }{{\displaystyle \zeta }}{}_k(t)-b{}_{jk}\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(t)-c{}_{jk}\zeta {}_k(t)-\\ {\displaystyle \int }{}_0^t\text{d}\tau \kappa {}_{jk}(t-\tau )\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(\tau )(22)\\ a{}_{jk}=-\rho {\displaystyle \underset{S{}_1}{\iint }\Psi }{}_{1k}(x{}_1,y{}_1,z{}_1)n{}_j\text{d}S(23)\\ b{}_{jk}=-\rho {\displaystyle \underset{S{}_1}{\iint }[}\Psi {}_{2k}(x{}_1,y{}_1,z{}_1)n{}_j-\Psi {}_{1k}(x{}_1,y{}_1,\\ z{}_1)m{}_j]\text{d}S(24)\\ c{}_{jk}=-\rho {\displaystyle \underset{S{}_1}{\iint }\Psi }{}_{2k}(x{}_1,y{}_1,z{}_1)m{}_j\text{d}S(25)\\ \kappa {}_{jk}(t)=\rho {\displaystyle \underset{S{}_1}{\iint }[}\frac{\partial \chi {}_k(x{}_1,y{}_1,z{}_1,t)}{\partial t}n{}_j-\\ \chi {}_k(x{}_1,y{}_1,z{}_1,t)m{}_j]\text{d}S(26)\end{array}$

式中: ρ为流体密度; n_j (j=1, 2, …, 6) 为广义法向量的j模态分量; m_j为恒定速度的j模态梯度; a_jk为由k模态运动引起的j模态下与船体几何形状有关的参数; b_jk、c_jk均为由k模态运动引起的j模态下与船体几何形状及航速有关的参数; κ_jk (t) 为与船体几何形状、航速和时间有关的参数。

由傅里叶变换^[10]得, 频域内附加质量A_jk (ω) 与阻尼系数B_jk (ω) 为

$\{\begin{array}{c}A{}_{jk}(\omega )=a{}_{jk}-\frac{1}{\omega }{\displaystyle \int }{}_0^{+\infty }\kappa {}_{jk}(\tau )\sin (\omega \tau )\text{d}\tau -\frac{c{}_{jk}}{\omega {}^2}\hfill \\ B{}_{jk}(\omega )=b{}_{jk}+{\displaystyle {\int }_0^{+\infty }\kappa }{}_{jk}(\tau )\cos (\omega \tau )\text{d}\tau \hfill \end{array}(27)$

式中: ω为波浪圆频率。

1.4   绕射问题求解

在参考坐标系下, 入射波速度势为

$\begin{array}{l}\text{ϕ}{}_0(x{}_1,y{}_1,z{}_1,t)=\frac{\text{i}\xi {}_{0}g}{\omega }\text{e}{}^{{\rm K}\left[z{}_1-\text{i}(x{}_1\cos (\alpha )+y{}_1\sin (\alpha ))\right]}\text{e}{}^{\text{i}\omega {}_{\text{e}}t}(28)\\ \omega {}_{\text{e}}=\omega -U{\rm K}\cos (\alpha )(29)\end{array}$

式中: α为浪向角; ξ₀为波幅; ω_e为遭遇频率。

原点处的入射波波幅ξ₁ (t) 为

$\xi {}_1(t)=\xi {}_0\text{e}{}^{\text{i}\omega {}_{\text{e}}t}(30)$

入射波波幅ξ₁ (t) 作为线性系统输入, W₁ (x₁, y₁, z₁, t) 为入射波速度势的速度场脉冲响应函数, 则入射波速度势的速度场^[11]可表示为

结合式(28)、(30) 和(31) 并通过傅里叶变换可得W₁ (x₁, y₁, z₁, t)。时域线性系统下任意入射波压力p (x₁, y₁, z₁, t) 为

$\begin{array}{l}p(x{}_1,y{}_1,z{}_1,t)={\displaystyle {\int }_{-\infty }^{+\infty }\text{d}}\tau p{}_1(x{}_1,y{}_1,z{}_1,\\ t-\tau )\xi {}_1(\tau )(32)\end{array}$

式中: p₁ (x₁, y₁, z₁, t) 为入射波压力的脉冲响应函数。

由线性Bernoulli方程可得参考坐标系下的入射波压力p (x₁, y₁, z₁, t) 为

$p(x{}_1,y{}_1,z{}_1,t)=\rho g\xi {}_0\text{e}{}^{{\rm K}\left[z{}_1-\text{i}(x{}_1\cos (\alpha )+y{}_1\sin (\alpha ))\right]}\text{e}{}^{\text{i}\omega {}_{\text{e}}t}$ (33)

结合式(32)、(33) 和傅里叶变换可得p₁ (x₁, y₁, z₁, t)。将入射波压力在船体湿表面上积分得到j模态Froude-Krylov力F_jI (t) 为

$\begin{array}{l}F{}_{j\text{Ι}}(t)={\displaystyle \underset{S{}_1}{\iint }p}(x{}_1,y{}_1,z{}_1,t)n{}_j\text{d}S=\\ {\displaystyle \int }{}_{-\infty }^{+\infty }\xi {}_1(\tau )\text{d}\tau {\displaystyle \underset{S{}_1}{\iint }p}{}_1(x{}_1,y{}_1,z{}_1,t-\tau )n{}_j\text{d}S(34)\end{array}$

j模态Froude-Krylov力F_jI (t) 的脉冲响应函数W_jI (t) 为

$W{}_{j\text{Ι}}(t)={\displaystyle \underset{S{}_1}{\iint }p}{}_1(x{}_1,y{}_1,z{}_1,t-\tau )n{}_j\text{d}S(35)$

则j模态Froude-Krylov力F_jI (t) 的脉冲表达式为

$F{}_{j\text{Ι}}(t)={\displaystyle \int }{}_{-\infty }^{+\infty }W{}_{j\text{Ι}}(t-\tau )\xi {}_1(\tau )\text{d}\tau (36)$

绕射速度势ϕ₇ (x₁, y₁, z₁, t) 应用脉冲响应方法表示为

ϕ₇ (x₁, y₁, z₁, t) =∫ ${}_{-\infty }^{+\infty }$ φ₇ (x₁, y₁, z₁, t-τ) ξ₁ (τ) dτ (37)

式中: φ₇ (x₁, y₁, z₁, t) 为绕射速度势ϕ₇ (x₁, y₁, z₁, t) 的脉冲响应函数。

由式(4)、(31) 和(37) 可得^[29]

$\frac{\partial \text{ϕ}{}_7(x{}_1,y{}_1,z{}_1,t)}{\partial \mathit{n}}=-\mathit{n}\mathit{W}{}_1(x{}_1,y{}_1,z{}_1,t-\tau )(38)$

结合式(19)、(31)、(37) 和(38) 便可求得φ₇ (x₁, y₁, z₁, t), 则j模态绕射力的脉冲响应函数W_j7 (t) 为

$\begin{array}{l}W{}_{j7}(t)={\displaystyle \underset{S{}_1}{\iint }\rho }[\phi {}_7(x{}_1,y{}_1,z{}_1,t)m{}_j-\\ \frac{\partial \phi {}_7(x{}_1,y{}_1,z{}_1,t)n{}_j}{\partial t}]\text{d}S(39)\end{array}$

则j模态波浪激励力F_jw (t) 由j模态Froude-Krylov力F_jI (t) 和j模态绕射力F_j7 (t) 组成, 即

F_jw (t) =F_jI (t) +F_j7 (t) =∫ ${}_{-\infty }^{+\infty }$ ζ₁ (τ) W_jI (t-τ) +W_j7 (t-τ) dτ (40)

1.5   运动微分方程求解

将船舶作为刚体考虑, 根据牛顿第二定律, 可得有航速船舶运动方程为

${\displaystyle \sum _{k=1}^6{\rm M}}{}_{jk}\stackrel{\cdot \cdot }{{\displaystyle \zeta }}{}_k(t)=F{}_j(t)(41)$

式中: F_j (t) 为j模态船舶所受的合力; M_jk为广义质量矩阵的元素。

将由k模态运动引起的j模态辐射力F_jk (t)、波浪激励力F_jw (t) 和静水恢复力F_js (t) 代入式(41) 可得

$\begin{array}{l}{\displaystyle \sum _{k=1}^6[}({\rm M}{}_{jk}+a{}_{jk})\stackrel{\cdot \cdot }{{\displaystyle \zeta }}{}_k(t)+b{}_{jk}\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(t)+(C{}_{jk}+c{}_{jk})\zeta {}_k(t)+\\ {\displaystyle {\int }_0^t\text{d}}\tau \kappa {}_{jk}(t-\tau )\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(\tau )]=F{}_{j\text{w}}(t)(42)\end{array}$

式中: C_jk为恢复力系数矩阵的元素。

在初始的短时间(一般设置为2个波浪遭遇周期) 内对式(42) 右端波浪力应用平滑函数, 以避免由于初始扰动造成的数值发散。运动微分方程可采用4阶Runge-Kutta法等数值方法求解, 最终得到稳定的船舶运动时间历程。

2.   三维时域Green函数计算

2.1   三维时域Green函数波动项计算

令μ=cos (θ) =- (z₁+z₂) /R₂ (θ为地顶角), q=KR₂, 量纲一时间β为$\sqrt{g/R{}_2}(t-\tau )$, 则式(15) 可以写为

$\begin{array}{l}G{}_1(x{}_1,y{}_1,z{}_1,x{}_2,y{}_2,z{}_2,t,\tau )=2\sqrt{\text{g}/R{}_2^3}f(\mu ,\beta )(43)\\ f(\mu ,\beta )={\displaystyle {\int }_0^{+\infty }\sqrt{q}}\sin (\beta \sqrt{q})\text{e}{}^{-q\mu }J{}_0(q\sqrt{1-\mu {}^2})\text{d}q(44)\end{array}$

将β划分为3个区间段, 分别为0≤β≤2、2 < β≤12和β > 12。当0≤β≤2时, f (μ, β) 为

$f(\mu ,\beta )={\displaystyle \sum _{n=0}^{+\infty }(-1)}{}^n\beta {}^{2n+1}\frac{(n+1)!}{(2n+1)!}{\rm P}{}_{n+1}(\mu )(45)$

式中: P_n (μ) 为关于μ的n阶Legendre函数。

当2 < β≤12时, f (μ, β) 满足关于β的四阶常微分方程^[12]为

$\begin{array}{l}\frac{\partial {}^{4}f(\mu ,\beta )}{\partial \beta {}^4}+\mu \beta \frac{\partial {}^{3}f(\mu ,\beta )}{\partial \beta {}^3}+\frac{\beta {}^2+16\mu }{4}\frac{\partial {}^{2}f(\mu ,\beta )}{\partial \beta {}^2}+\\ \frac{7\beta }{4}\frac{\partial f(\mu ,\beta )}{\partial \beta }+\frac{7f(\mu ,\beta )}{4}=0(46)\end{array}$

采用式(45) 计算出f (μ, β) 及其1~3阶导数在β=2时的值并作为式(46) 的初值, 接着采用文献[23]中提出的精细积分法求解式(46)。

当β > 12时, f (μ, β) 为

$\begin{array}{l}f(\mu ,\beta )=\left(\frac{\text{i}}{\beta }\right){}^3{\displaystyle \sum _{n=0}^{+\infty }\frac{(2n+2)!}{n!}}\frac{2}{\beta {}^{2n}}{\rm P}{}_n(\mu )+\\ \frac{\text{e}{}^{-\beta {}^2\mu /4}}{\sqrt{2\sqrt{1-\mu {}^2}}}{\displaystyle \sum _{n=0}^{+\infty }\frac{2}{(\sqrt{1-\mu {}^2}){}^n}}\cdot \\ {\displaystyle \sum _{n=0}^{+\infty }d}{}_{mn}\text{e}{}^{\text{i}\theta {}_{mn}}\left(\frac{2}{\beta }\right){}^{2m+2n-1}(47)\\ \theta {}_{mn}=\frac{\beta {}^2}{4}\sqrt{1-\mu {}^2}+\left(\frac{3}{4}-\frac{2m+n}{2}\right)\text{π}+\\ \left(m+2n-\frac{3}{2}\right)\theta (48)\\ c{}_n=\frac{\left[\Gamma (n+1/2)\right]{}^2}{2{}^n\text{π}n!}(49)\\ d{}_{mn}=\{\begin{array}{cc}\frac{c{}_n(1-2n)!}{(1-2m-2n)!2{}^{2m}m!}\hfill & 1-2n>0\hfill \\ \frac{c{}_n(2m+2n-2)!}{(2n-2)!2{}^{2m}m!}\hfill & 1-2n\le 0\hfill \end{array}(50)\end{array}$

式中: Γ (·) 为伽马函数; m为整数变量。

2.2   三维时域Green函数波动项节点制表

申亮等采用4阶Runge-Kutta法求解式(46) ^[25], 本文采用精细积分法^[24]求解式(46)。2种方法均以式(45) 的计算结果作为式(46) 的初值。当μ=0时, f (0, β) 解析解为

$\begin{array}{l}f(0,\beta )=\frac{\text{π}\beta {}^3}{16\sqrt{2}}[J{}_{\frac{1}{4}}\left(\frac{\beta {}^2}{8}\right)J{}_{-\frac{1}{4}}\left(\frac{\beta {}^2}{8}\right)+\\ J{}_{\frac{3}{4}}\left(\frac{\beta {}^2}{8}\right)J{}_{-\frac{3}{4}}\left(\frac{\beta {}^2}{8}\right)](51)\end{array}$

式中: $J{}_{\frac{1}{4}}$、$J{}_{-\frac{1}{4}}$、$J{}_{\frac{3}{4}}$和$J{}_{-\frac{3}{4}}$分别为第1类$\frac{1}{4}$、$-\frac{1}{4}$、$\frac{3}{4}$、$-\frac{3}{4}$阶贝塞尔函数。

统一以精细积分法求解式(46), 作为4阶Runge-Kutta法和精细积分法求解式(46) 的初值, 计算步长Δβ=0.01。

表 1为4阶Runge-Kutta法和精细积分法的计算结果与解析解的相对误差, 可知: 在相同步长和初始值下, 在过渡时间区域采用精细积分法所得结果的精度比4阶Runge-Kutta法有极大的提高。

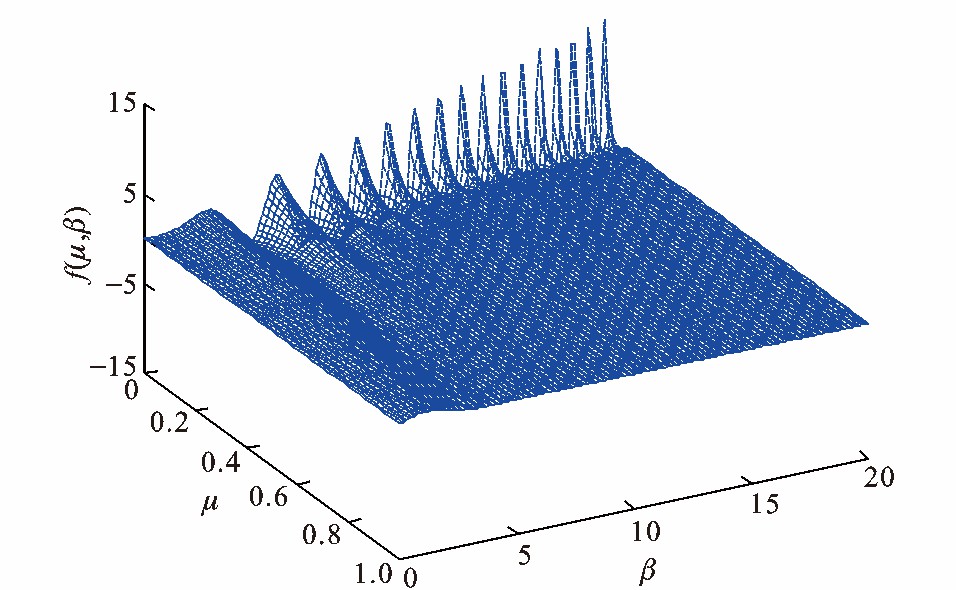
表  1  不同方法计算所得f (0, β) 的相对误差

Table  1.  Relative errors of f (0, β) calculated by different methods

计算方法	β取值不同时各方法计算结果与解析解的相对误差
	2.53	6.26	9.15	12.48
4阶Runge-Kutta法	3.0×10-5	2.9×10-2	-2.5×10-2	6.8×10-3
精细积分法	1.3×10-16	4.7×10-14	6.3×10-15	-5.1×10-14

下载: 导出CSV 

| 显示表格

图 2为本文方法计算所得f (μ, β), 可知: 当场点与源点靠近或位于水面时, 即μ较小时, f (μ, β) 在β方向上具有强烈的振荡增幅特性; 随着μ的逐渐增大, 其在β方向上的振荡幅度逐渐变小; f (μ, β) 变化趋势符合三维时域Green函数波动项的性质, 可验证本文三维时域Green函数波动项节点制表的可靠性。

图  2  f (μ, β) 的计算结果

Figure  2.  Calculation result of f (μ, β)

下载: 全尺寸图片 幻灯片

f (μ, β) 可以写为^[29]

$f(\mu ,\beta )=\text{e}{}^{-\beta {}^2\mu /4}f(0,\beta )+f{}_0(\mu ,\beta )(52)$

式中: f₀ (μ, β) 为f (μ, β) 中变化平缓的部分。

经过数值试验可知, 将f (0, β) 按式(51) 进行计算并以二进制文本形式存储, 其中计算步长Δβ取0.001, 此时线性插值即可满足精度要求。将f₀ (μ, β) 在μ、β方向上以适当的均匀间隔存储, 经过数值试验可得, 取计算步长Δμ、Δβ分别为0.005、0.010时即可满足工程精度要求。同理, 可以得到三维时域Green函数波动项空间和时间导数的制表。

3.   数值模拟结果分析

3.1   仿真对象

为验证在航海模拟器中建立船舶运动模型的可靠性, 在迎浪海况下, 当船舶前进航速的Froude数为0.2时, 对Wigley Ⅰ型船舶和S60型船舶进行仿真, 2种船型的主要参数见表 2, 面元分布分别见

图 3、4。

表  2  Wigley Ⅰ型船舶与S60型船舶的参数

Table  2.  Parameters of Wigley Ⅰand S60 hulls

船型	船长L/m	船宽/m	吃水/m	排水量/m3	纵摇惯性半径	重心距离基线距离/m	方形系数
Wigley Ⅰ	3	0.3	0.187 5	0.094 6	0.25L	0.17	0.56
S60	140	20	8	15 680	0.25L	8	0.70

下载: 导出CSV 

| 显示表格

图  3  Wigley Ⅰ型船舶面元分布

Figure  3.  Panel distribution of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  4  S60型船舶面元分布

Figure  4.  Panel distribution of S60 hull

下载: 全尺寸图片 幻灯片

3.2   辐射问题分析

对比影响船舶运动性能较大的水动力系数(包括附加质量和阻尼系数) A₃₃、B₃₃、A₅₅和B₅₅, 其量纲一形式A′₃₃、B′₃₃、A′₅₅、B′₅₅和波浪圆频率ω的量纲一形式ω′分别为

$\begin{array}{l}{A}^{\prime }{}_{33}=A{}_{33}/(\rho V)(53)\\ B^{\prime }{}_{33}=\frac{B{}_{33}\sqrt{L/g}}{\rho V}(54)\\ A^{\prime }{}_{55}=A{}_{55}/(\rho VL{}^2)(55)\\ B^{\prime }{}_{55}=\frac{B{}_{55}\sqrt{L/g}}{\rho VL{}^2}(56)\\ {\omega }^{\prime }=\omega \sqrt{L/g}(57)\end{array}$

式中: V为船舶排水体积。

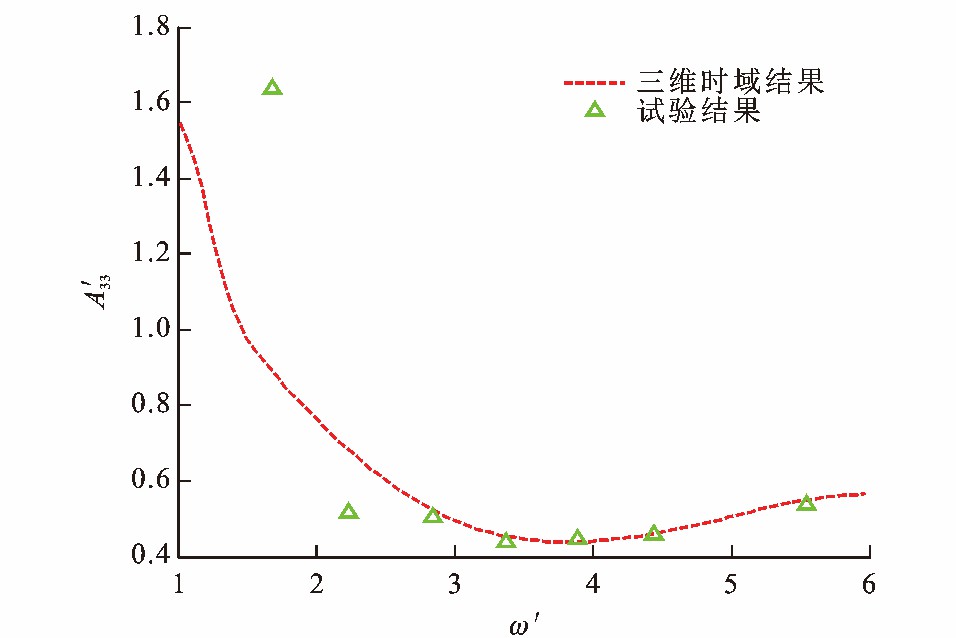
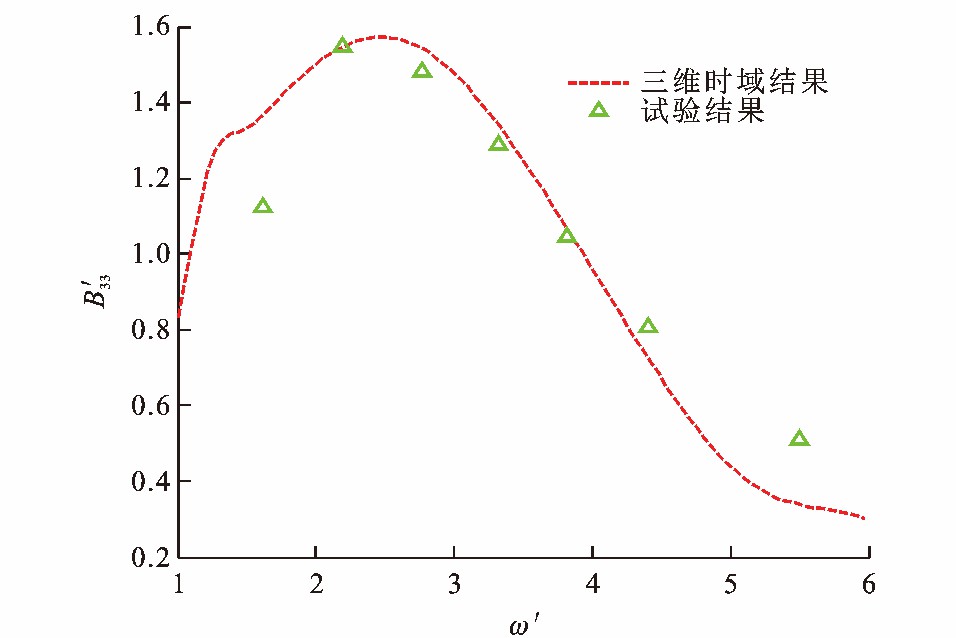
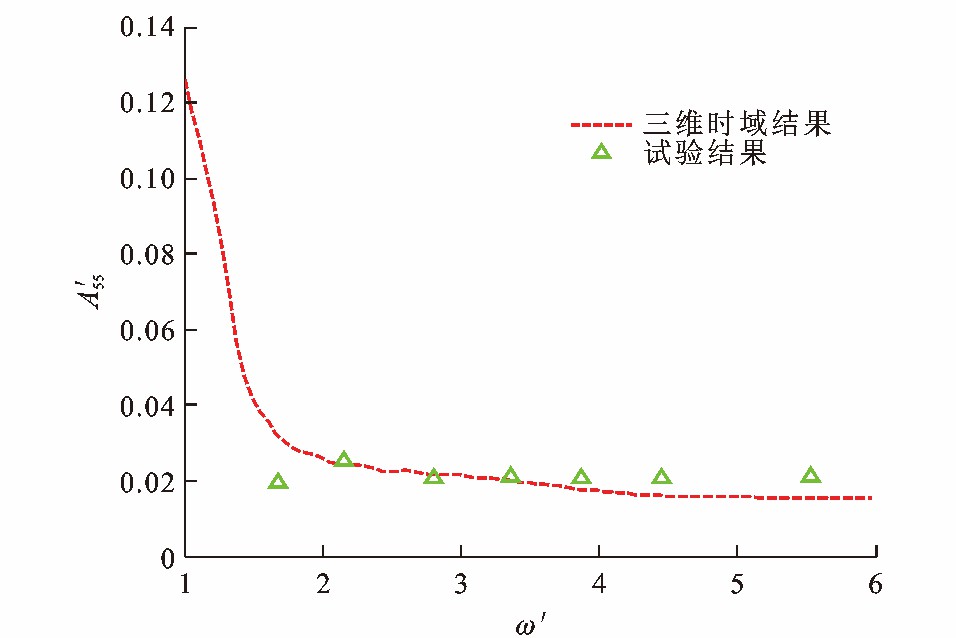
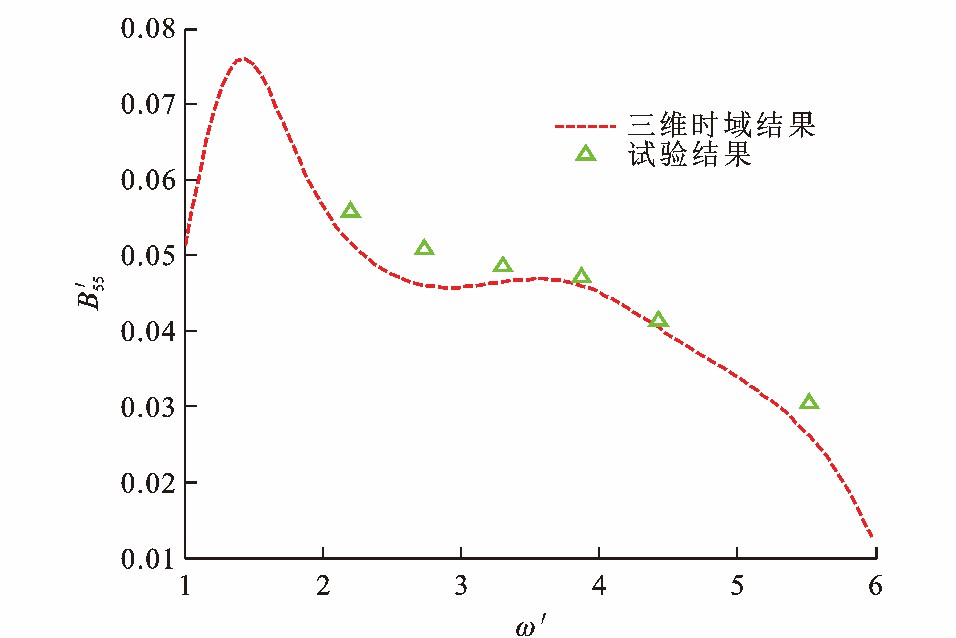
图 5~8为Wigley Ⅰ型船舶水动力系数, 可知: 由于不规则频率的影响, 在低频处, 当量纲一频率为1.7时, 垂荡附加质量计算结果比试验结果低44%, 垂荡阻尼系数和纵摇阻尼系数计算结果分别比试验结果高21%和67%;随着量纲一频率的增加, 垂荡附加质量与阻尼系数的大部分数值计算结果与试验值的相对误差小于20%。可见, Wigley Ⅰ型船舶的水动力系数计算结果与文献[30]中的试验值在大部分频率范围内能较好地吻合。

图  5  Wigley Ⅰ型船舶量纲一垂荡附加质量

Figure  5.  Dimensionless heave added masses of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  6  Wigley Ⅰ型船舶量纲一垂荡阻尼系数

Figure  6.  Dimensionless heave damping coefficients of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  7  Wigley Ⅰ型船舶量纲一纵摇附加质量

Figure  7.  Dimensionless pitch added masses of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  8  Wigley Ⅰ型船舶量纲一纵摇阻尼系数

Figure  8.  Dimensionless pitch damping coefficients of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

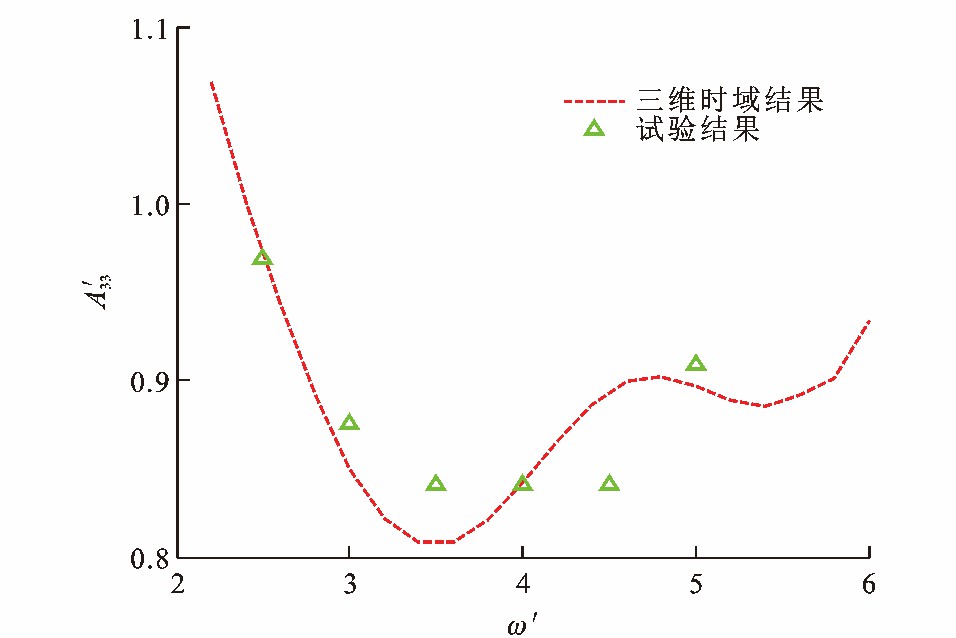
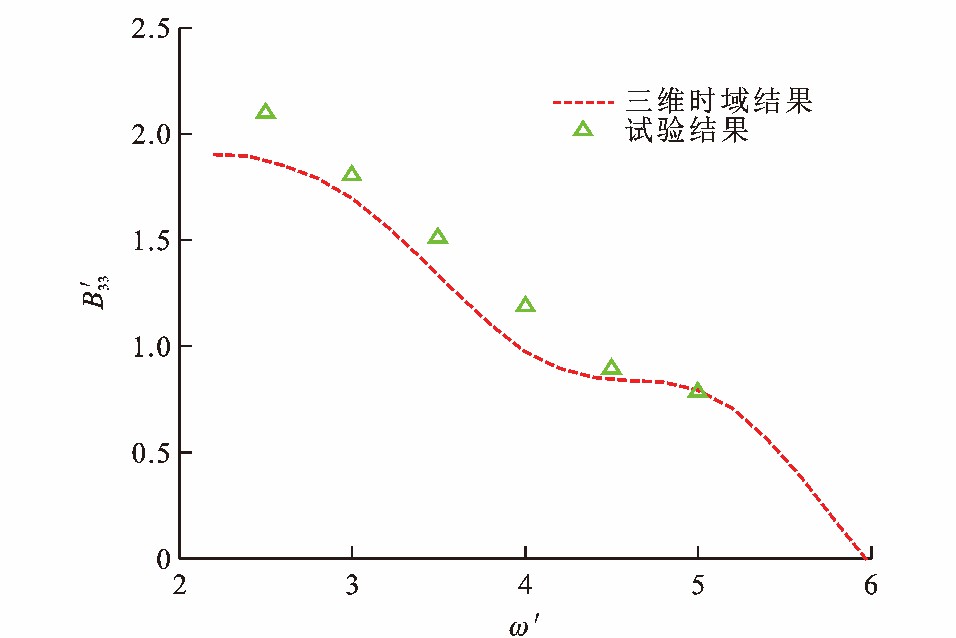
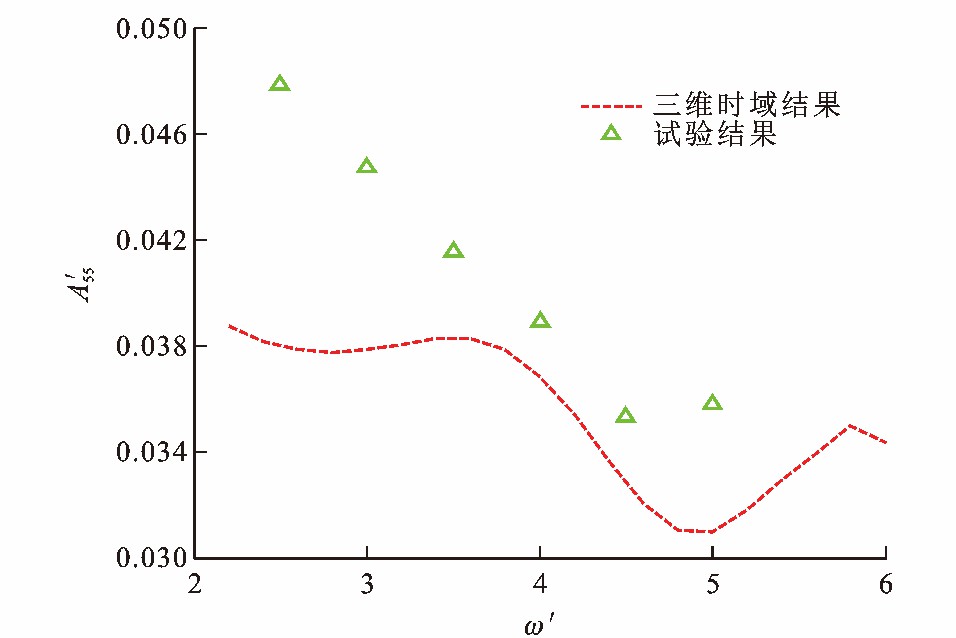
图 9~12为S60型船舶水动力系数, 可知: 由于不规则频率的影响, 在低频处, 当量纲一频率为2.5时, 纵摇附加质量和纵摇阻尼系数的计算结果分别比试验结果低21%和43%;随着量纲一频率的增加, 垂荡附加质量与阻尼系数的大部分数值计算结果与试验值的相对误差小于30%。可见, S60型船舶的水动力系数计算结果与文献[31]中的试验值在大部分频率范围内能较好地吻合。

图  9  S60型船舶量纲一垂荡附加质量

Figure  9.  Dimensionless heave added masses of S60 hull

下载: 全尺寸图片 幻灯片

图  10  S60型船舶量纲一垂荡阻尼系数

Figure  10.  Dimensionless heave damping coefficients of S60 hull

下载: 全尺寸图片 幻灯片

图  11  S60型船舶量纲一纵摇附加质量

Figure  11.  Dimensionless pitch added masses of S60 hull

下载: 全尺寸图片 幻灯片

图  12  S60型船舶量纲一纵摇阻尼系数

Figure  12.  Dimensionless pitch damping coefficients of S60 hull

下载: 全尺寸图片 幻灯片

3.3   绕射问题分析

对波浪激励力进行傅里叶变换可以得到垂荡波浪力的频响函数F_3w (ω_e) 与纵摇波浪力的频响函数F_5w (ω_e) 的量纲一形式F′_3w和F′_5w分别为

$\begin{array}{l}{F}^{\prime }{}_{3\text{w}}=F{}_{3\text{w}}\omega {}_{\text{e}}L/(\rho gV\xi {}_0)(58)\\ F^{\prime }{}_{5\text{w}}=F{}_{5\text{w}}\omega {}_{\text{e}}/(\rho gV\xi {}_0)(59)\end{array}$

图  13  Wigley Ⅰ型船舶量纲一垂荡波浪力幅值

Figure  13.  Dimensionless heave wave exciting force amplitudes of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  14  Wigley Ⅰ型船舶量纲一纵摇波浪力幅值

Figure  14.  Dimensionless pitch wave exciting force amplitudes of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图 13、14为Wigley Ⅰ型船舶所受波浪激励力, 其中KL为波数的量纲一形式, 可知: Wigley Ⅰ型船舶所受的垂荡波浪力与纵摇波浪力的频率响应的数值计算结果与试验值的相对误差小于10%。

图  15  S60型船舶量纲一垂荡波浪力幅值

Figure  15.  Dimensionless heave wave exciting force amplitudes of S60 hull

下载: 全尺寸图片 幻灯片

图  16  S60型船舶量纲一纵摇波浪力幅值

Figure  16.  Dimensionless pitch wave exciting force amplitudes of S60 hull

下载: 全尺寸图片 幻灯片

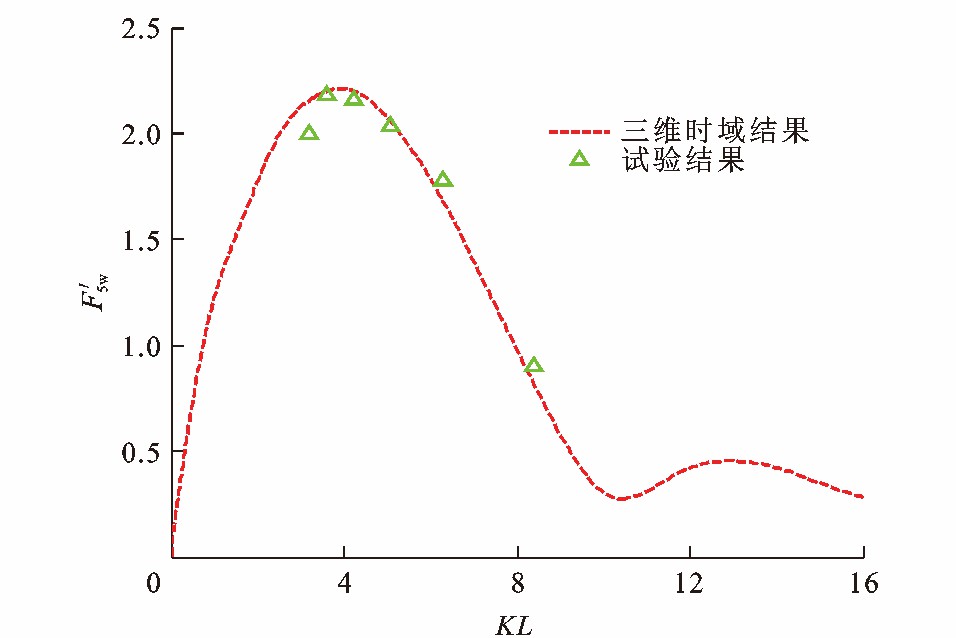
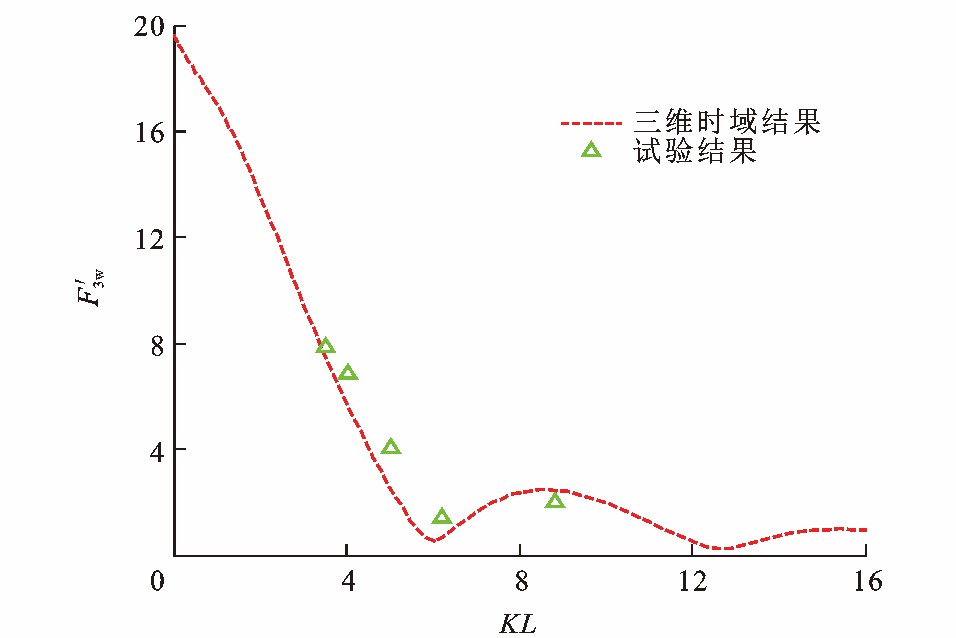
图 15、16为S60型船舶所受波浪激励力幅值, 可知: S60型船舶所受的垂荡波浪力与纵摇波浪力的频响函数的大部分计算结果与试验值的相对误差小于20%, 二者吻合较好。

3.4   规则波浪中船舶的运动仿真

为与文献[30]中的试验结果对比, 本文只对Wigley Ⅰ型船舶进行垂荡和纵摇2个自由度的运动数值模拟, 垂荡位移ζ₃、纵摇位移ζ₅和时间t的量纲一形式ζ′₃、ζ′₅和t′分别为

$\begin{array}{l}{\zeta }^{\prime }{}_3=\zeta {}_3/\zeta {}_0(60)\\ {\zeta }^{\prime }{}_5=\zeta {}_{5}L/(2\text{π}\zeta {}_0)(61)\\ t^{\prime }=t/{\rm T}{}_{\text{w}}(62)\end{array}$

式中: T_w为遭遇周期。

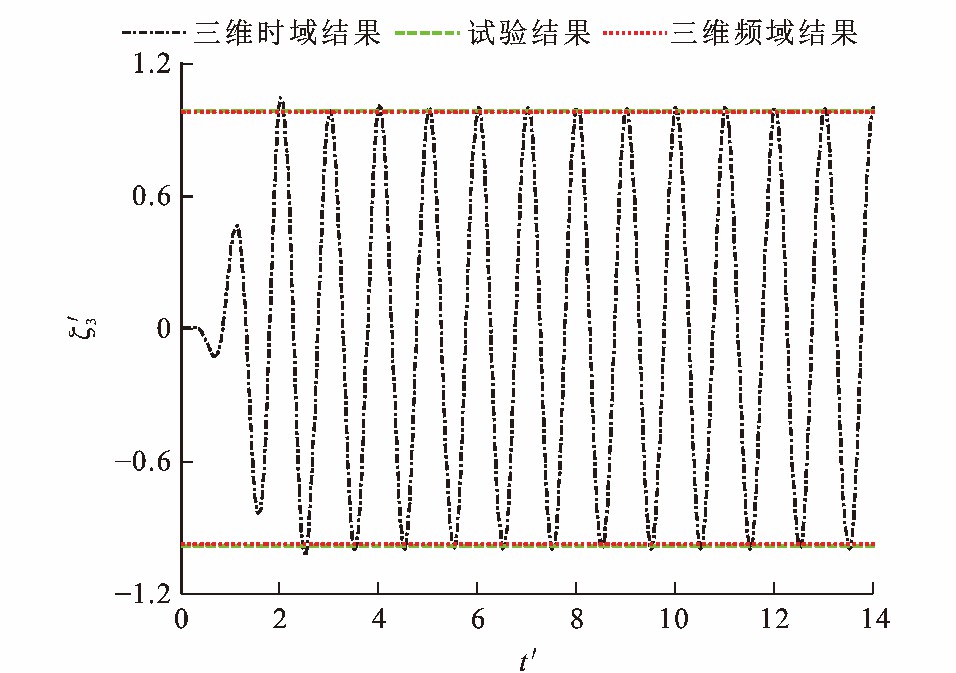
波浪参数设定: 波幅ξ₀为0.018 m; 波长λ与船长比λ/L分别为1.25、1.50和2.00;浪向角α为π。图 17~22为Wigley Ⅰ型船舶在不同波长处14个周期的垂荡纵摇运动的响应时间历程, 可知: 当λ/L=1.25时, 三维时域方法计算的垂荡幅值响应因子和纵摇幅值响应因子分别比试验值低11.3%和4.8%, 三维频域方法计算的垂荡幅值响应因子比试验值高48.4%, 纵摇幅值响应因子比试验值低48.4%;当λ/L=1.50时, 三维时域方法计算的垂荡幅值响应因子和纵摇幅值响应因子分别比试验值低3.0%和11.3%, 三维频域方法计算的垂荡幅值响应因子比试验值高9.8%, 纵摇幅值响应因子比试验值低23.6%;当λ/L=2.0时, 三维时域方法计算的垂荡幅值响应因子比试验值高1.6%, 纵摇幅值响应因子比试验低7.3%, 三维频域方法计算的垂荡幅值响应因子和纵摇幅值响应因子分别比试验值低0.5%和7.3%;经过3~5个波浪遭遇周期之后, 初始瞬时扰动效应渐渐消失, 运动时间历程趋于平稳, 证明了本文开发的三维时域数值程序的稳定性; 入射波较长时, 本文的三维时域方法和三维频域方法均可得到较好的船舶运动数值解, 但入射波长较短时, 三维时域方法比三维频域方法更接近试验值; 入射波较短时^[6], 绕射力与辐射力合力占船体受力比例较大, 对船舶运动影响较大; 采用三维频域方法求解绕射力与辐射力时, 由于有航速频域Green函数数值求解复杂且误差较大, 最终造成船舶运动预报误差较大。综上所述, 本文提出的三维时域方法较三维频域方法具有更强的适用性。

图  17  λ/L为1.25时Wigley Ⅰ型船舶量纲一垂荡运动时间历程

Figure  17.  Dimensionless heave motion time histories of Wigley Ⅰ hull when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  18  λ/L为1.25时Wigley Ⅰ型船舶量纲一纵摇运动时间历程

Figure  18.  Dimensionless pitch motion time histories of Wigley Ⅰ hull when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  19  λ/L为1.50时Wigley Ⅰ型船舶量纲一垂荡运动时间历程

Figure  19.  Dimensionless heave motion time histories of Wigley Ⅰ hull when λ/L is 1.50

下载: 全尺寸图片 幻灯片

图  20  λ/L为1.50时Wigley Ⅰ型船舶量纲一纵摇运动时间历程

Figure  20.  Dimensionless pitch motion time histories of Wigley Ⅰ hull when λ/L is 1.50

下载: 全尺寸图片 幻灯片

图  21  λ/L为2.0时Wigley Ⅰ型船舶量纲一垂荡运动时间历程

Figure  21.  Dimensionless heave motion time histories of Wigley Ⅰ hull when λ/L is 2.0

下载: 全尺寸图片 幻灯片

图  22  λ/L为2.0时Wigley Ⅰ型船舶量纲一纵摇运动时间历程

Figure  22.  Dimensionless pitch motion time histories of Wigley Ⅰ hull when λ/L is 2.0

下载: 全尺寸图片 幻灯片

4.   结语

(1) 在线性时域理论范畴内, 本文基于三维时域Green函数法, 为航海模拟器建立可靠实用的船舶在规则波中的运动数学模型, 可以进一步提高航海模拟器的行为真实感。

(2) 在数值计算三维时域Green函数时, 在大、小时间过渡区域采用精细积分法, 其数值精度较4阶Runge-Kutta法有较大提高。特别是当μ=0时, 采用精细积分法的数值计算结果精度较4阶Runge-Kutta法提高了至少10个数量级。进一步将三维时域Green函数分为解析表达的波动剧烈项与可以插值调用的波动平缓项, 并根据实际工程应用进行节点制表, 可为三维时域内研究船舶水动力系数和运动提供有效的求解器。

(3) 通过对Wigley Ⅰ型船舶和S60型船舶进行水动力分析与运动数值计算, 水动力系数与波浪力频响函数的数值结果与试验结果吻合良好。对于Wigley Ⅰ型船舶运动响应预报, 当λ/L=1.25时, 采用三维频域方法计算所得垂荡纵摇幅值响应因子比试验值大48.4%, 而采用三维线性时域方法计算所得垂荡幅值响应因子和纵摇幅值响应因子分别比试验值低11.3%和4.8%, 与试验结果吻合良好, 因此, 基于三维时域方法所构建的船舶运动数学模型具有较强的工程适用性。

(4) 在海况恶劣情况时, 船舶摇荡运动较为剧烈, 具有强非线性的运动特性, 此时线性理论难以满足建模要求, 因此, 如何为航海模拟器建立船舶非线性运动数学模型是下一步研究的重点。