基于动态流场数据的虚拟港口建模方法

陈立家; 王凯; 魏天明; 郝国柱

doi:10.19818/j.cnki.1671-1637.2022.02.023

基于动态流场数据的虚拟港口建模方法

doi: 10.19818/j.cnki.1671-1637.2022.02.023

陈立家^{1, 2,},
王凯¹,
魏天明^{1, 2},
郝国柱^{1, 2}

1.
武汉理工大学航运学院，湖北武汉 430063
2.
武汉理工大学内河航运技术湖北省重点实验室，湖北武汉 430063

基金项目:

国家重点研发计划 2018YFC0810400

国家重点研发计划 2018YFC1407400

详细信息

作者简介:
陈立家(1979-)，男，湖北武汉人, 武汉理工大学副教授, 工学博士, 从事智能航海与仿真技术研究

中图分类号: U661
计量
- 文章访问数: 698
- HTML全文浏览量: 291
- PDF下载量: 66
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-13
- 刊出日期: 2022-04-25

Virtual port modeling method based on dynamic fluid field data

CHEN Li-jia^{1, 2
,},
WANG Kai¹,
WEI Tian-ming^{1, 2},
HAO Guo-zhu^{1, 2}

1.
School of Navigation, Wuhan University of Technology, Wuhan 430063, Hubei, China
2.
Hubei Key Laboratory of Inland Shipping Technology, Wuhan University of Technology, Wuhan 430063, Hubei, China

Funds:

National Key Research and Development Program of China 2018YFC0810400

National Key Research and Development Program of China 2018YFC1407400

More Information

Author Bio:
CHEN Li-jia(1979-), male, associate professor, PhD, navisky@qq.com

摘要

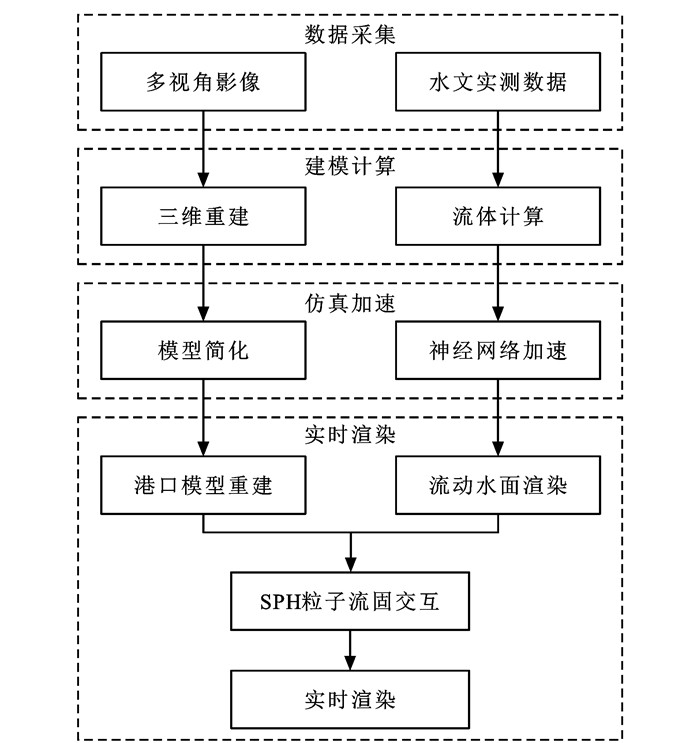
摘要: 为了实现港口数字化升级，提出了一种基于动态流场数据的虚拟港口建模方法；采用三维重建模型从无人机倾斜摄影影像数据中重建了港口几何特征，获取高精度三维模型；引入了基于二次误差度量的边折叠算法简化模型，以避免数据量过大致使渲染效率低的问题；分析了欧拉法数值计算过程中的高耗时环节，建立了神经网络模型学习流场演化特征，加速投影项计算得到实时变化的流场数据，通过流场数据驱动水流动态渲染，结合光滑粒子流体动力学方法表现水流与船舶、陆地的交互动态，在保证渲染实时性的同时，提高渲染真实感。研究结果表明：重建的港口三维重建模型顶点数量可达3 320 937个，重建的网格模型在Meshlab中渲染频率为78.7 Hz；经过模型简化降低90.0%的模型顶点数量后，模型顶点数量缩减为332 836个，渲染频率提升至108.7 Hz，模型简化后几何误差小于2.0%；在256×256的流场网格下，采用神经网络加速的网格流体计算方法所得水流速度场平均更新间隔约为17 ms，平均仿真精度为88.6%；通过开源图像引擎驱动流场数据和港口三维模型，平均渲染频率可达50.5 Hz。可见，该方法可有效解决高精度实时渲染中的关键问题，以达到仿真精度与渲染效率间的动态平衡，在精度损失较小的情况下实现较高精度的虚拟港口建模与实时动态仿真。
- 虚拟港口 /
- 三维重建 /
- 神经网络 /
- 倾斜摄影 /
- 水流模拟
Abstract: To achieve the digital upgradation of ports, a virtual port modeling method based on the dynamic flow field data was proposed. The geometric feature of a port was reconstructed by the three-dimensional (3D) reconstruction model with the aerial image data of unmanned aerial vehicle (UAV) oblique photography, and a high-precision 3D model was established. The simplified model of the edge collapse algorithm based on the quadric error metric was introduced to prevent low rendering efficiency caused by the data overflow. The high time consuming step in the numerical calculation of Euler method was analyzed. A neural network model was built to learn the evolution feature of the flow field. The calculation of the projection term was accelerated to produce the dynamic flow field data that were used to drive the dynamic rendering of water flow. The smoothed particle hydrodynamics (SPH) method was employed to reflect the interactions of water flow with ships and land. In this way, not only was the real-time performance of rendering ensured, but also the realistic effect of rendering was improved. Research results show that the 3D reconstruction model of the reconstructed port has 3 320 937 vertices, and the rendering frequency of the reconstructed grid model is 78.7 Hz in Meshlab. After almost 90.0% of the vertices are removed from the model via model simplification, the number of vertices reduces to 332 836, and the rendering frequency enhances to 108.7 Hz. The geometric errors of the model are smaller than 2.0% after simplification. In a 256×256 flow field grid, the average update interval is roughly 17 ms for the water flow velocity field obtained by the grid fluid calculation method accelerated by a neural network, and the average simulation precision is 88.6%. When the flow field data and 3D port model were driven by an open scene graph (OSG) engine, the average rendering frequency can reach 50.5 Hz. In conclusion, the proposed method can effectively solve the key problems in high-precision real-time rendering to achieve the dynamic balance between simulation precision and rendering efficiency. It enables high-precision virtual port modeling and real-time dynamic simulation without great precision loss. 1 tab, 11 figs, 30 refs.
- virtual port /
- 3D reconstruction /
- neural network /
- oblique photography /
- water flow simulation

HTML全文

图 1 技术路线

Figure 1. Technology roadmap

下载: 全尺寸图片幻灯片

图 2 三维重建流程

Figure 2. Flow of 3D reconstruction

下载: 全尺寸图片幻灯片

图 3 边折叠

Figure 3. Edge collapse

下载: 全尺寸图片幻灯片

图 4 神经网络结构

Figure 4. Structure of neural network

下载: 全尺寸图片幻灯片

图 5 流固交互算法

Figure 5. Fluid-solid interaction algorithm

下载: 全尺寸图片幻灯片

图 6 模型简化

Figure 6. Models simplification

下载: 全尺寸图片幻灯片

图 7 实时流场

Figure 7. Real-time fluid fields

下载: 全尺寸图片幻灯片

图 8 尹公洲航段水文观测断面布置

Figure 8. Hydrological observation section distributions of Yingongzhou Channel

下载: 全尺寸图片幻灯片

图 9 水流特征对比

Figure 9. Comparison of flow characteristics

下载: 全尺寸图片幻灯片

图 10 动态水流渲染

Figure 10. Renderings of dynamic fluid

下载: 全尺寸图片幻灯片

图 11 虚拟港口渲染

Figure 11. Rendering of virtual port

下载: 全尺寸图片幻灯片

表 1 简化前后模型特征对比

Table 1. Comparison of characteristics of models before and after simplification

模型特征	原始模型	简化模型	几何尺度变化率/%
顶点数量/个	3 320 937	332 836	-89.978
面片数量/个	6 567 919	656 790	-90.000
表面积/m²	363 362	359 538	-1.053
模型体积/m³	6 016 083	5 989 922	-0.435
质心横坐标/m	12.026	11.839	-1.653
质心纵坐标/m	20.062	20.086	0.116
质心垂坐标/m	-270.646	-270.654	-0.003

下载: 导出CSV

参考文献(30)

[1]	TAO Fei, QI Qing-lin, WANG Li-hui, et al. Digital twins and cyber-physical systems toward smart manufacturing and industry 4.0: correlation and comparison[J]. Engineering, 2019, 5(4): 653-661. doi: 10.1016/j.eng.2019.01.014
[2]	AUSTIN M, DELGOSHAEI P, COELHO M, et al. Architecting smart city digital twins: combined semantic model and machine learning approach[J]. Journal of Management in Engineering, 2020, 36(4): 04020026. doi: 10.1061/(ASCE)ME.1943-5479.0000774
[3]	VARELA J M, GUEDES SOARES C. Geometry and visual realism of ship models for digital ship bridge simulators[J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2017, 231(1): 329-341. doi: 10.1177/1475090216642470
[4]	ZHAI Xiao-ming, YIN Yong, SHEN He-long. Modeling and rendering of river in inland river ship handling simulator[C]//IEEE. 2017 International Conference on Information, Cybernetics and Computational Social Systems. New York: IEEE, 2017: 444-449.
[5]	丁晶, 赵玮丹, 曾珍. 三维港口GIS的场景组织与建设过程模拟[J]. 测绘与空间地理信息, 2016, 39(5): 27-29, 34. doi: 10.3969/j.issn.1672-5867.2016.05.008 DING Jing, ZHAO Wei-dan, ZENG Zhen. Scene organization and construction process simulation of 3D harbor GIS[J]. Geomatics and Spatial Information Technology, 2016, 39(5): 27-29, 34. (in Chinese) doi: 10.3969/j.issn.1672-5867.2016.05.008
[6]	刘海宁, 刘成良, 李彦明, 等. 基于GPS/GIS的虚拟港口可视化建模[J]. 上海交通大学学报, 2009, 43(6): 866-870. doi: 10.3321/j.issn:1006-2467.2009.06.003 LIU Hai-ning, LIU Cheng-liang, LI Yan-ming, et al. Visual modeling of virtual container terminal based on GPS/GIS[J]. Journal of Shanghai Jiaotong University, 2009, 43(6): 866-870. (in Chinese) doi: 10.3321/j.issn:1006-2467.2009.06.003
[7]	ZHANG Shang-hong, ZHANG Tian-xiang, WU Yu, et al. Three-dimensional waterway system for ship navigation based on integrated virtual waterway and flow simulation[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2017, 143(1): 04016011. doi: 10.1061/(ASCE)WW.1943-5460.0000354
[8]	CALÌ M, AMBU R. Advanced 3D photogrammetric surface reconstruction of extensive objects by UAV camera image acquisition[J]. Sensors, 2018, 18(9): 2815. doi: 10.3390/s18092815
[9]	JAMES M R, ROBSON S. Straightforward reconstruction of 3D surfaces and topography with a camera: accuracy and geoscience application[J]. Journal of Geophysical Research: Earth Surface, 2012, 117: F03017. doi: 10.1029/2011JF002289
[10]	QU Yu-fu, HUANG Jian-yu, ZHANG Xuan. Rapid 3D reconstruction for image sequence acquired from UAV camera[J]. Sensor, 2018, 18(1): 255. doi: 10.3390/s18010255
[11]	INZERILLO L, DI MINO G, ROBERTS R. Image-based 3D reconstruction using traditional and UAV datasets for analysis of road pavement distress[J]. Automation in Construction, 2018, 96: 457-469. doi: 10.1016/j.autcon.2018.10.010
[12]	VACONDIO R, DAL PALÙ A, FERRARI A, et al. A non-uniform efficient grid type for GPU-parallel shallow water equations models[J]. Environmental Modelling and Software, 2017, 88: 119-137. doi: 10.1016/j.envsoft.2016.11.012
[13]	ABGRALL R, BACIGALUPPI P, TOKAREVA S. High-order residual distribution scheme for the time-dependent Euler equations of fluid dynamics[J]. Computers and Mathematics with Applications, 2019, 78(2): 274-297. doi: 10.1016/j.camwa.2018.05.009
[14]	PENG Jun, ZHAI Chuan-lei, NI Guo-xi, et al. An adaptive characteristic-wise reconstruction WENO-Z scheme for gas dynamic Euler equations[J]. Computers and Fluids, 2019, 179: 34-51. doi: 10.1016/j.compfluid.2018.08.008
[15]	HE Yi, BAYLY A E, HASSANPOUR A, et al. A GPU-based coupled SPH-DEM method for particle-fluid flow with free surfaces[J]. Powder Technology, 2018, 338: 548-562. doi: 10.1016/j.powtec.2018.07.043
[16]	DUAN Xing-feng, REN Hong-xiang, LI Hai-jiang. Incompressible fluids simulation by relaxing the density-invariant condition in a marine simulator[J]. Mathematical Problems in Engineering, 2019, 2019: 8971089. https://www.hindawi.com/journals/mpe/2019/8971089/
[17]	GAO Yang, LI Shuai, HAO Ai-min, et al. Simulating multi-scale, granular materials and their transitions with a hybrid Euler-Lagrange solver[J]. IEEE Transactions on Visualization and Computer Graphics, 2021, 27(12): 4483-4494. doi: 10.1109/TVCG.2021.3107597
[18]	LIU Qiang, QIN Yi, LI Guo-dong. Fast simulation of large-scale floods based on GPU parallel computing[J]. Water, 2018, 10(5): 589. doi: 10.3390/w10050589
[19]	YANG Cheng, YANG Xu-bo, XIAO Xiang-yun. Data-driven projection method in fluid simulation[J]. Computer Animation and Virtual Worlds, 2016, 27(3/4): 415-424. doi: 10.1007/978-3-319-41217-7_17
[20]	肖祥云. 基于深度神经网络的流体动画研究[D]. 上海: 上海交通大学, 2019. XIAO Xiang-yun. Research on deep neural network based fluid simulation[D]. Shanghai: Shanghai Jiaotong University, 2019. (in Chinese)
[21]	LI Z J, FARIMANI A B. Graph neural network-accelerated Lagrangian fluid simulation[J]. Computers and Graphics, 2022, 103: 201-211. doi: 10.1016/j.cag.2022.02.004
[22]	段兴锋. 航海场景中基于物理的海浪建模与绘制[D]. 大连: 大连海事大学, 2019. DUAN Xing-feng. Modeling and rendering for physical-based ocean wave in navigation scene[D]. Dalian: Dalian Maritime University. (in Chinese)
[23]	ZHANG Xue-quan, LIU Jin, HU Zi-he, et al. Flow modeling and rendering to support 3D river shipping based on cross-sectional observation data[J]. International Journal of Geo-Information, 2020, 9(3): 156. doi: 10.3390/ijgi9030156
[24]	陈立家, 刘锭坤, 田延飞, 等. 面向船舶操纵模拟器的内河水流三维建模与仿真[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(4): 634-639. doi: 10.3963/j.issn.2095-3844.2020.04.009 CHEN Li-jia, LIU Ding-kun, TIAN Yan-fei, et al. 3D modeling and simulation of inland water flow for ship manipulation simulator[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2020, 44(4): 634-639. (in Chinese) doi: 10.3963/j.issn.2095-3844.2020.04.009
[25]	陈立家, 王凯, 李世刚, 等. 基于航空影像的航海模拟器视景快速建模方法[J]. 系统仿真学报, 2021, 33(7): 1565-1573. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202107008.htm CHEN Li-jia, WANG Kai, LI Shi-gang, et al. A fast maritime simulator scene modeling method based on aerial images[J]. Journal of System Simulation, 2021, 33(7): 1565-1573. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202107008.htm
[26]	PREVITALI M, DÍAZ VILARIÑO L, SCAIONI M. Indoor building reconstruction from occluded point clouds using graph-cut and ray-tracing[J]. Applied Sciences, 2018, 8(9): 1529. doi: 10.3390/app8091529
[27]	GARLAND M, HECKBERT P S. Simplifying surfaces with color and texture using quadric error metrics[C]//IEEE. Proceedings of the 1998 IEEE Visualization Conference. New York: IEEE, 1998: 263-269.
[28]	陈勇, 刘培艺, 李颖, 等. 大规模真实感固流交互实时绘制方法[J]. 计算机辅助设计与图形学学报, 2020, 32(3): 378-384. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF202003005.htm CHEN Yong, LIU Pei-yi, LI Ying, et al. Real-time rendering algorithm for large-scale realistic solid-fluid interaction[J]. Journal of Computer-Aided Design and Computer Graphics, 2020, 32(3): 378-384. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF202003005.htm
[29]	MINTGEN F, MANHART M. A bi-directional coupling of 2D shallow water and 3D Reynolds-averaged Navier-Stokes models[J]. Journal of Hydraulic Research, 2018, 56(6): 771-785. doi: 10.1080/00221686.2017.1419989
[30]	TOMPSON J, SCHLACHTER K, SPRECHMANN P, et al. Accelerating Eulerian fluid simulation with convolutional networks[C]//ICLR. 5th International Conference on Learning Representations. La Jolla: ICLR, 2017: 3424-3433.