基于多链竞争差分进化算法的无砟轨道结构有限元模型修正

叶玲; 江宏康; 陈华鹏; 冯宇轩; 王力骋

doi:10.19818/j.cnki.1671-1637.2024.02.007

基于多链竞争差分进化算法的无砟轨道结构有限元模型修正

doi: 10.19818/j.cnki.1671-1637.2024.02.007

1.
华东交通大学轨道交通基础设施性能监测与保障国家实验室，江西南昌 330013
2.
江西交投咨询集团有限公司，江西南昌 330108

基金项目:

国家自然科学基金项目 52008168

详细信息

作者简介:
叶玲(1989-)，女，湖北京山人，华东交通大学讲师，工学博士，从事结构健康监测与轨道动力学研究

中图分类号: U239.5
计量
- 文章访问数: 429
- HTML全文浏览量: 68
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2023-11-08
- 网络出版日期: 2024-05-16
- 刊出日期: 2024-04-30

Finite element model correction for ballastless track structure based on multi-chain competition based differential evolution algorithm

1.
State Key Laboratory of Performance Monitoring and Protecting of Rail Transit Infrastructure, East China Jiaotong University, Nanchang 330013, Jiangxi, China
2.
Jiangxi Transport Investment Consulting Group Co., Ltd., Nanchang 330108, Jiangxi, China

Funds:

National Natural Science Foundation of China 52008168

More Information

Author Bio:
YE Ling(1989-), female, assistant professor, PhD, 58718070@qq.com

摘要

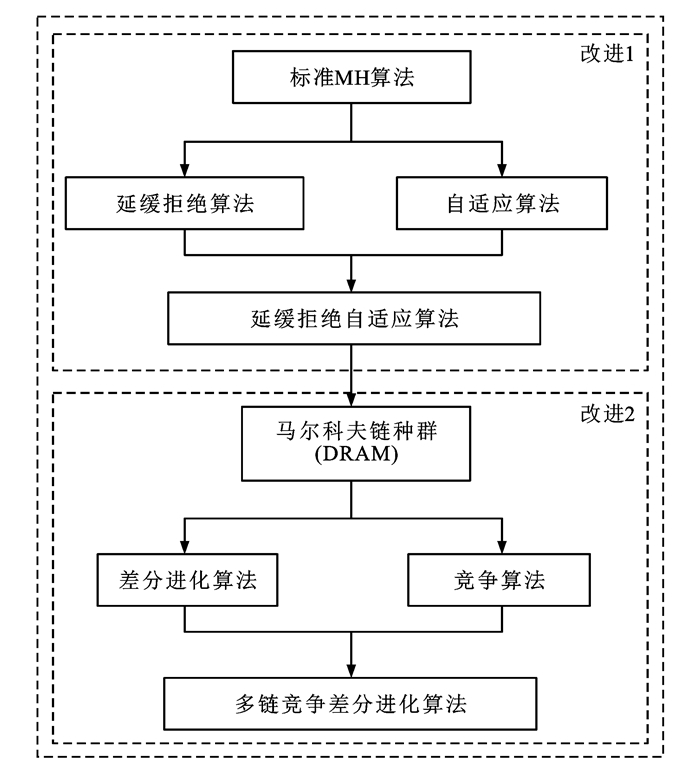
摘要: 为获得更接近真实情况的轨道结构模型，提出了一种基于多链竞争差分进化算法的无砟轨道结构有限元模型修正方法；以频率振型模态为响应建立了适用于无砟轨道结构的目标函数和似然函数，以标准马尔科夫链蒙特卡罗算法为基础，引入多链差分进化算法来解决高维参数模型效率低和收敛难的问题；引进竞争算法，利用竞争决出的失败者向胜利者学习的机制，不断迭代修正钢轨模型以提高修正精度；在此基础上，通过一个无砟轨道结构有限元模型修正数值算例验证所提方法的高效性。分析结果表明：采用Metropolis-Hastings算法和延缓拒绝自适应Metropolis算法修正后，单元参数与真实值间的最大相对误差分别为4.75%和1.35%，而采用多链竞争差分进化算法修正后，单元参数与真实值间的最大相对误差为0.28%，且模态振型向量之间的相关性接近1，说明多链竞争差分进化算法的修正精度优于另外2种算法；在分别加噪5%、10%和15%的噪声测试中，采用Metropolis-Hastings算法和延缓拒绝自适应Metropolis算法修正后，参数误差达到了9%左右，而采用多链竞争差分进化算法模型修正后，参数误差均在5%以内，进一步证明了多链竞争差分进化算法良好的鲁棒性。由此可见，多链竞争差分进化算法可以为解决复杂环境导致测试信息不完备的无砟轨道结构有限元模型修正提供一种新手段。
- 轨道交通 /
- 轨道结构模型修正 /
- 多链竞争差分进化算法 /
- 无砟轨道 /
- 结构健康监测
Abstract: To obtain a more realistic track structure model, a finite element model correction method for the ballastless track structure based on a multi-chain competition based differential evolution algorithm was proposed. The objective function and likelihood function suitable for the ballastless track structure were established according to the response of frequency vibration mode. Based on the standard Markov Chain Monte Carlo algorithm, a multi-chain differential evolution algorithm was introduced to solve the problems of low efficiency and difficult convergence in high-dimensional parameter models. Then, the competitive algorithm was introduced, and the mechanism of learning from the winners by the losers determined by the competition was utilized, so as to continuously iteratively correct the track model and thus improve the correction accuracy. On this basis, the efficiency of the proposed method was verified by a numerical example of the finite element model correction of the ballastless track structure. Analysis results show that after correction using the Metropolis-Hastings algorithm and the delayed rejection adaptive Metropolis algorithm, the maximum relative errors between the corrected unit parameters and the true values are 4.75% and 1.35%, respectively. However, the maximum relative error between the corrected unit parameters and the true values is 0.28%, after correction using the multi-chain competition based differential evolution algorithm. In addition, the correlation between vibration mode vectors is close to 1, indicating that the correction accuracy of the multi-chain competition based differential evolution algorithm is better than the other two algorithms. In the noise tests with 5%, 10%, and 15% noise, respectively, the parameter errors reach about 9% after corrected by the Metropolis-Hastings algorithm and the delayed rejection adaptive Metropolis algorithm, while those corrected by the multi-chain competition based differential evolution algorithm are all within 5%. It further proves the good robustness of the multi-chain competition based differential evolution algorithm. Therefore, the multi-chain competition based differential evolution algorithm can provide a new method for correcting the finite element model of ballastless tracks with incomplete testing information caused by complex environments.
- rail transit /
- model correction for track structure /
- multi-chain competition based differential evolution algorithm /
- ballastless track /
- structural health monitoring

HTML全文

图 1 算法改进过程

Figure 1. Algorithm improvement process

下载: 全尺寸图片幻灯片

图 2 算法流程

Figure 2. Flow of algorithm

下载: 全尺寸图片幻灯片

图 3 钢轨模型单元划分

Figure 3. Unit division for rail model

下载: 全尺寸图片幻灯片

图 4 轨道单元模型

Figure 4. Track unit model

下载: 全尺寸图片幻灯片

图 5 一阶测试频率均值

Figure 5. Mean values of first-order test frequency

下载: 全尺寸图片幻灯片

图 6 归一化二阶振型均值

Figure 6. Mean values of normalized second-order vibration mode

下载: 全尺寸图片幻灯片

图 7 修正前后三阶振型对比

Figure 7. Comparison of third-order vibration modes before and after correction

下载: 全尺寸图片幻灯片

图 8 DRAM算法和多链CB-DE算法修正后θ₇的频数对比

Figure 8. Comparison of frequencies of θ₇ corrected by DRAM algorithm and multi-chain CB-DE algorithm

下载: 全尺寸图片幻灯片

图 9 MH算法修正过程

Figure 9. Correction process of MH algorithm

下载: 全尺寸图片幻灯片

图 10 DRAM算法修正过程

Figure 10. Correction process of DRAM algorithm

下载: 全尺寸图片幻灯片

图 11 多链CB-DE算法修正过程

Figure 11. Correction process of multi-chain CB-DE algorithm

下载: 全尺寸图片幻灯片

图 12 加噪5%、10%和15%的一阶模态频率

Figure 12. First-order mode frequencies with 5%, 10%, and 15% noise

下载: 全尺寸图片幻灯片

图 13 不同噪声下3种算法修正后参数θ₃的误差

Figure 13. Errors of parameter θ₃ corrected by three algorithms under different noises

下载: 全尺寸图片幻灯片

表 1 CRTS Ⅱ型无砟轨道参数

Table 1. Parameters of CRTS Ⅱ ballastless track

部件	参数	取值
钢轨	质量/(kg·m^-1)	60
	弹性模量/MPa	2.06×10⁵
	截面惯性矩/m⁴	0.321 7×10^-4
	横截面积/m²	7.745×10^-3
轨道板	长度/m	6.45
	宽度/m	2.55
	厚度/m	0.2
	密度/(kg·m^-3)	2 500
	弹性模量/MPa	3.9×10⁵
路基	刚度系数/(MN·m)	60
路基	阻尼系数/(kN·s·m^-1)	90
垫板	刚度系数/(MN·m)	60
垫板	阻尼系数/(kN·s·m^-1)	50
CA砂浆	刚度系数/(MN·m)	900
CA砂浆	阻尼系数/(kN·s·m^-1)	83
混凝土支承层	长度/m	6.45
	宽度/m	2.95
	厚度/m	0.3
	密度/(kg·m^-3)	2 500
	弹性模量/MPa	3.0×10⁴

下载: 导出CSV

表 2 待修正参数的真实值

Table 2. True values of parameters to be corrected

单元	1	2	3	4	5
真实值	1.2E₀	1.4E₀	1.6E₀	1.8E₀	2.0E₀

单元	6	7	8	9	10
真实值	2.2E₀	2.4E₀	2.6E₀	2.8E₀	3.0E₀

下载: 导出CSV

表 3 各阶频率均值与标准差

Table 3. Mean values and standard deviations of frequencies at different orders

阶数	均值/Hz	标准差/Hz	变异系数/%
1	8.985	0.006 3	0.07
2	10.673	0.018 0	0.17
3	12.580	0.016 0	0.13
4	14.174	0.010 0	0.07
5	15.022	0.035 0	0.23
6	21.693	0.019 0	0.09

下载: 导出CSV

表 4 三种算法的频率修正结果对比

Table 4. Comparison of frequency correction results among three algorithms

阶数	测试均值/Hz	MH		DRAM		多链CB-DE
阶数	测试均值/Hz	均值/Hz	相对误差/%	均值/Hz	相对误差/%	均值/Hz	相对误差/%
1	8.985	8.876	1.21	8.981	0.04	8.960	0.28
2	10.673	10.547	1.18	10.670	0.03	10.678	0.05
3	12.580	12.476	0.83	12.570	0.08	12.583	0.02
4	14.174	14.847	4.75	14.344	1.20	14.178	0.03
5	15.022	14.890	0.88	15.225	1.35	15.008	0.09
6	21.693	21.561	0.61	21.553	0.65	21.691	0.01

下载: 导出CSV

表 5 三种算法修正后振型的MAC对比

Table 5. Comparison of MACs of vibration modes corrected by three algorithms

阶数	1	2	3	4
MH	0.991	0.993	0.989	0.993
DRAM	0.998	0.997	0.992	0.995
多链CB-DE	0.999	0.999	0.998	0.998

下载: 导出CSV

表 6 三种算法的参数修正结果对比

Table 6. Comparison of parameter correction results among three algorithms

参数	真实值	初始值	MH	DRAM	多链CB-DE
θ₁	1.20E₀	4.34E₀	1.12E₀	1.25E₀	1.20E₀
θ₂	1.40E₀	4.91E₀	1.41E₀	1.39E₀	1.40E₀
θ₃	1.60E₀	3.75E₀	1.46E₀	1.58E₀	1.62E₀
θ₄	1.80E₀	2.20E₀	1.78E₀	1.81E₀	1.80E₀
θ₅	2.00E₀	4.59E₀	1.95E₀	1.98E₀	1.99E₀
θ₆	2.20E₀	4.53E₀	2.16E₀	2.19E₀	2.19E₀
θ₇	2.40E₀	3.50E₀	2.40E₀	2.43E₀	2.40E₀
θ₈	2.60E₀	4.12E₀	2.67E₀	2.59E₀	2.59E₀
θ₉	2.80E₀	1.80E₀	2.80E₀	2.82E₀	2.80E₀
θ₁₀	3.00E₀	4.89E₀	3.01E₀	2.98E₀	3.00E₀

下载: 导出CSV

表 7 不同噪声下参数θ₃的修正误差

Table 7. Correction errors of parameter θ₃ under different noises %

加噪值/%	5	10	15
MH	1.41	5.20	8.21
DRAM	1.22	5.03	8.05
多链CB-DE	0.84	2.61	5.11

下载: 导出CSV

参考文献(31)

[1]	GOULET J A, KOO K. Empirical validation of Bayesian dynamic linear models in the context of structural health monitoring[J]. Journal of Bridge Engineering, 2018, 23(2): 05017017. doi: 10.1061/(ASCE)BE.1943-5592.0001190
[2]	KAMARIOTIS A, CHATZI E, STRAUB D. Value of information from vibration-based structural health monitoring extracted via Bayesian model updating[J]. Mechanical Systems and Signal Processing, 2022, 166: 108465. doi: 10.1016/j.ymssp.2021.108465
[3]	王佐才, 丁雅杰, 戈壁, 等. 桥梁结构非线性模型修正研究综述[J]. 交通运输工程学报, 2022, 22(2): 59-75. doi: 10.19818/j.cnki.1671-1637.2022.02.004 WANG Zuo-cai, DING Ya-jie, GE Bi, et al. Review on nonlinear model updating for bridge structures[J]. Journal of Traffic and Transportation Engineering, 2022, 22(2): 59-75. (in Chinese). doi: 10.19818/j.cnki.1671-1637.2022.02.004
[4]	SOHN H, LAW K H. A Bayesian probabilistic approach for structure damage detection[J]. Earthquake Engineering and Structural Dynamics, 1997, 26(12): 1259-1281. doi: 10.1002/(SICI)1096-9845(199712)26:12<1259::AID-EQE709>3.0.CO;2-3
[5]	房长宇, 张耀庭. 基于参数不确定性的预应力混凝土梁模型修正[J]. 华中科技大学学报(自然科学版), 2011, 39(11): 87-91. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201111019.htm FANG Chang-yu, ZHANG Yao-ting. Model updating of prestressed concrete beams using parameters uncertainty[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(11): 87-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201111019.htm
[6]	BECK J L, KATAFYGIOTIS L S. Updating models and their uncertainties. Ⅰ: Bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998, 124(4): 455-461. doi: 10.1061/(ASCE)0733-9399(1998)124:4(455)
[7]	BEHMANESH I, MOAVENI B. Probabilistic identification of simulated damage on the Dowling Hall Footbridge through Bayesian finite element model updating[J]. Structural Control and Health Monitoring, 2015, 22(3): 463-483. doi: 10.1002/stc.1684
[8]	LAM H F, YANG Jia-hua, AU S K. Bayesian model updating of a coupled-slab system using field test data utilizing an enhanced Markov chain Monte Carlo simulation algorithm[J]. Engineering Structures, 2015, 102: 144-155. doi: 10.1016/j.engstruct.2015.08.005
[9]	YANG Jia-hua, LAM H F, BECK J L. Bayes-Mode-ID: a Bayesian modal-component-sampling method for operational modal analysis[J]. Engineering Structures, 2019, 189: 222-240. doi: 10.1016/j.engstruct.2019.03.047
[10]	刘纲, 罗钧, 秦阳, 等. 基于改进MCMC方法的有限元模型修正研究[J]. 工程力学, 2016, 33(6): 138-145. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201606018.htm LIU Gang, LUO Jun, QIN Yang, et al. A finite element model updating method based on improved MCMC method[J]. Engineering Mechanics, 2016, 33(6): 138-145. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201606018.htm
[11]	WAN Hua-ping, REN Wei-xin. Stochastic model updating utilizing Bayesian approach and Gaussian process model[J]. Mechanical Systems and Signal Processing, 2016, 70/71: 245-268. doi: 10.1016/j.ymssp.2015.08.011
[12]	LIU Zeng-yu, YANG Jia-hua, LAM H F, et al. A Markov chain Monte Carlo-based Bayesian framework for system identification and uncertainty estimation of full-scale structures[J]. Engineering Structures, 2023, 295: 116886. doi: 10.1016/j.engstruct.2023.116886
[13]	宋彦朋, 陈辉, 黄斌. 基于贝叶斯的钢筋混凝土梁模型修正方法[J]. 土木工程与管理学报, 2019, 36(4): 126-132, 139. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ201904020.htm SONG Yan-peng, CHEN Hui, HUANG Bin. Finite element model updating method of reinforced concrete beam based on Bayesian method[J]. Journal of Civil Engineering and Management, 2019, 36(4): 126-132, 139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ201904020.htm
[14]	WANG Xiao-you, HOU Rong-rong, XIA Yang, et al. Structural damage detection based on variational Bayesian inference and delayed rejection adaptive Metropolis algorithm[J]. Structural Health Monitoring, 2021, 20(4): 1-18.
[15]	REN Wei-xin, DE ROECK G. Structural damage identification using modal data. Ⅱ: test verification[J]. Journal of Structural Engineering, 2002, 128(1): 96-104. doi: 10.1061/(ASCE)0733-9445(2002)128:1(96)
[16]	MALEKGHAINI N, GHAHARI F, EBRAHIMIAN H, et al. Time-domain finite element model updating for operational monitoring and damage identification of bridges[J]. Structural Control and Health Monitoring, 2023, 2023: 4170149.
[17]	彭珍瑞, 郑捷, 白钰, 等. 一种基于改进MCMC算法的模型修正方法[J]. 振动与冲击, 2020, 39(4): 236-245. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202004031.htm PENG Zhen-rui, ZHENG Jie, BAI Yu, et al. A model updating method based on an improved MCMC algorithm[J]. Journal of Vibration and Shock, 2020, 39(4): 236-245. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202004031.htm
[18]	WU Ling-zi, JI Wen-ying, ABOURIZKS M. Bayesian inference with Markov chain Monte Carlo-based numerical approach for input model updating[J]. Journal of Computing in Civil Engineering, 2020, 34(1): 04019043. doi: 10.1061/(ASCE)CP.1943-5487.0000862
[19]	江守燕, 赵林鑫, 杜成斌. 基于频率和模态保证准则的结构内部多缺陷反演[J]. 力学学报, 2019, 51(4): 1091-1100. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201904012.htm JIANG Shou-yan, ZHAO Lin-xin, DU Cheng-bin. Identification of multiple flaws in structures based on frequency and modal assurance criteria[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1091-1100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201904012.htm
[20]	翁顺, 朱宏平. 基于有限元模型修正的土木结构损伤识别方法[J]. 工程力学, 2021, 38(3): 1-16. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202103002.htm WENG Shun, ZHU Hong-ping. Damage identification of civil structures based on finite element model updating[J]. Engineering Mechanics, 2021, 38(3): 1-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202103002.htm
[21]	易伟建, 周云, 李浩. 基于贝叶斯统计推断的框架结构损伤诊断研究[J]. 工程力学, 2009, 26(5): 121-129. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200905022.htm YI Wei-jian, ZHOU Yun, LI Hao. Damage assessment research on frame structure based on Bayesian statistical inference[J]. Engineering Mechanics, 2009, 26(5): 121-129. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200905022.htm
[22]	YUEN K V. Recent developments of Bayesian model class selection and applications in civil engineering[J]. Structural Safety, 2010, 32(5): 338-346. doi: 10.1016/j.strusafe.2010.03.011
[23]	CHEUNG S H, BECK J L. Bayesian model updating using hybrid Monte Carlo simulation with application to structural dynamic models with many uncertain parameters[J]. Journal of Engineering Mechanics, 2009, 135(4): 243-255. doi: 10.1061/(ASCE)0733-9399(2009)135:4(243)
[24]	SHERRI M, BOULKAIBET I, MARWALA T, et al. Bayesian finite element model updating using a population Markov chain Monte Carlo algorithm[J]. Special Topics in Structural Dynamics and Experimental Techniques, 2021, 5: 259-269.
[25]	郝燕玲, 单志明, 沈锋. 基于DRAM算法的α稳定分布参数估计[J]. 华中科技大学学报(自然科学版), 2011, 39(10): 73-78. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201110019.htm HAO Yan-ling, SHAN Zhi-ming, SHEN Feng. Parameter estimation of α-stable distributions using DRAM algorithm[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(10): 73-78. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201110019.htm
[26]	SHERRI M, BOULKAIBET I, MARWALA T, et al. Bayesian finite element model updating using an improved evolution Markov chain algorithm[J]. Model Validation and Uncertainty Quantification, 2022, 3: 163-174.
[27]	WENTWORTH M T, SMITH R C, WILLIAMS B. Bayesian model calibration and uncertainty quantification for an HIV model using adaptive metropolis algorithms[J]. Inverse Problems in Science and Engineering, 2018, 26(2): 233-256. doi: 10.1080/17415977.2017.1312365
[28]	TERBRAAK C J F T. A Markov chain Monte Carlo version of the genetic algorithm differential evolution: easy Bayesian computing for real parameter spaces[J]. Statistics and Computing, 2006, 16(3): 239-249. doi: 10.1007/s11222-006-8769-1
[29]	吴神花, 雷晓燕. 交叉迭代算法求解车辆-轨道非线性耦合方程的收敛性讨论[J]. 华东交通大学学报, 2015, 32(3): 23-31. https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201503005.htm WU Shen-hua, LEI Xiao-yan. Convergence condition of cross iterative algorithm for vehicle-track nonlinear coupling equations[J]. Journal of East China Jiaotong University, 2015, 32(3): 23-31. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HDJT201503005.htm
[30]	孙璐, 段雨芬, 高培培. 高速铁路板式无砟轨道的结构分析模型对比[J]. 东南大学学报(自然科学版), 2013, 43(5): 938-943. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201305007.htm SUN Lu, DUAN Yu-fen, GAO Pei-pei. Comparison of structural analysis models for slab ballastless track in high-speed railway[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(5): 938-943. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201305007.htm
[31]	叶玲, 陈华鹏, 刘昌雨. 基于子结构的轨道系统基础结构参数识别方法[J]. 铁道学报, 2022, 44(5): 91-100. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202205012.htm YE Ling, CHEN Hua-peng, LIU Chang-yu. Parameter identification of rail transit infrastructure based on substructure method[J]. Journal of the China Railway Society, 2022, 44(5): 91-100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB202205012.htm