-
摘要: 针对中国提速铁路采用的CH160-0简单链型悬挂接触网及SS7受电弓, 建立接触网的有限元模型, 计算得出固有频率及相应的模态振型, 导出其振动方程, 并推导出受电弓非线性模型的运动微分方程, 利用泰勒级数展开对非线性模型进行线性化, 得到受电弓框架的等效参数, 最后在这个基础上建立起受电弓/接触网垂向耦合动力学模型。应用受电弓的线性模型及非线性模型, 而且考虑机车、轨道激扰因素影响下, 对接触网/受电弓系统的动态进行了运行模拟计算并加以比较。Abstract: For the civil CH160-0 simple stitched catenary on the high speed railway and SS7 pantograph, the finite element model of the catenary is sep up. The natural frequency and the corresponding mode are calculated and the equation of the vibration is educed. The nonlinear dynamical differential equation of the pantograph is list. By the Taylor series, the nonlinear model is linearized and the equivalent parameters of the frame of the pantograph are gained. The vertical coupling dynamic model of the pantograph/catenary system is established. Based on the linear model and the nonlinear model of the pantograph, the computation and the comparison of the simulation on the dynamic characteristic of the pantograph/catenary system are come out with the vibrating responses of the locomotive and track taken into consideration.
-
Key words:
- pantograph /
- catenary /
- coupling /
- dynamics /
- nonlinear /
- linearization
-
图 4 受电弓/接触网垂向耦合动力学模型
Figure 4. The vertical coupling dynamic model of the pantograph/catenary system
图 6 受电弓为线性、非线性模型时接触力及位移的变化情况
Figure 6. The variation of the contact force and the displacement on the condition of the nonlinear/linear pantogrph
图 7 受电弓为线性、非线性模型时频谱分析结果
Figure 7. The result of the frequency-phase analysis on the condition of the nonlinear/linear pantogrph
图 8 机车顶部位移振动响应
Figure 8. The response of the displacement on the top of the locomotive
图 9 线性模型时接触力的变化曲线
Figure 9. The variable curve of the contact force on the linear pantograph
图 10 非线性模型时接触力的变化曲线
Figure 10. The variable curve of the contact force on the nonlinear pantograph
表 1 SS7受电弓基本参数
Table 1. The elementary parameters of the SS7 pantograph
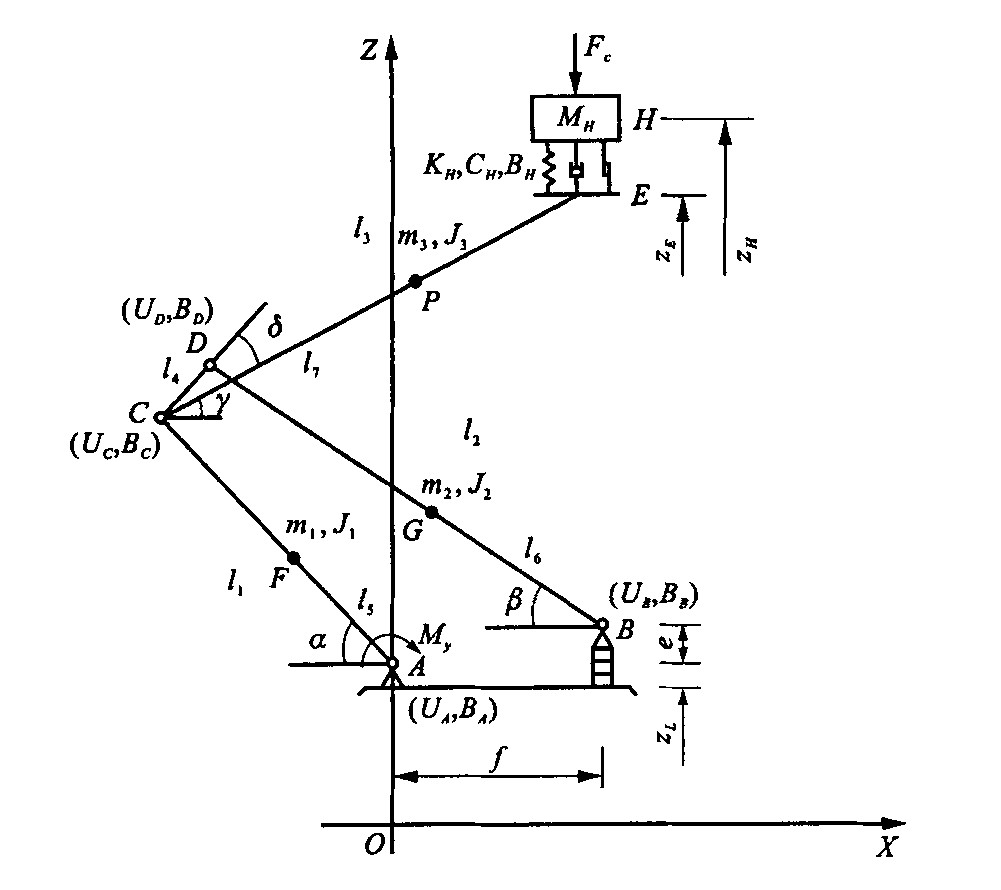
l1 l2 l3 l4 l5 l6 l7 δ 1.470 1.634 2.063 0.227 0.631 0.960 0.998 31.96° m1 m2 m3 J1 J2 J3 e f 20 11.5 25.5 4.199 0.884 17.247 0.270 0.345 MH KH CH BH MF KF CF BF 15 7600 0 0 20 0 0 0 
下载: 导出CSV
表 2 CH160-0接触网基本参数
Table 2. The elementary parameters of the CH160-0 catenary
材料 横截面积/mm2 弹性模量/Pa 线密度/kg·m-1 张力/kN 承力索 GLJC120/35 153 0.817×1011 0.602 17 接触线 RiS120 120 1.3×1011 1.07 13 跨数 5 跨距/m 65 结构高度/m 1.5
下载: 导出CSV
表 3 接触网前50阶固频率(Hz)
Table 3. The frontal 50th frequencies of the catenary
1~10 0.92955 0.94428 0.97522 0.97524 1.0021 1.8137 1.8523 1.9020 1.9451 1.9612 11~20 2.6956 2.7548 2.8326 2.9012 2.9287 3.5434 3.6281 3.7332 3.8303 3.8725 21~30 4.3436 4.4607 4.5863 4.7049 4.7633 5.1154 5.2296 5.3491 5.4525 5.4990 31~40 5.7884 5.8005 5.8667 5.9263 5.9653 6.0021 6.6829 6.6830 6.6831 6.6834 41~50 6.6835 6.7146 6.7153 6.7158 6.8159 6.8183 6.8835 6.8878 6.8978 6.9065
下载: 导出CSV
-
[1] 梅桂明. 受电弓/接触网垂向耦合动力学研究[D]. 成都: 西南交通大学, 2001. [2] 章新生, 杨宝全, 姚金先. 电力机车受电弓的静接触压力曲线及安全保护问题[J]. 材料开发与应用, 1994, 9 (2): 38-41. https://www.cnki.com.cn/Article/CJFDTOTAL-CLKY402.006.htm [3] MANABE K, MORIKAWA T, HIKITA M. On dynamics of overhead equipment and multi-pantograph system[J]. Quarterly Reports of RTRI, 1986, 27(1): 21-25. [4] VINAYAGALINGAM T. Computer evaluation of controlled pantographs for current collection from simple catenary overhead equipment at high speed[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 1983, 105: 287-294. doi: 10.1115/1.3140673 [5] LINK M, NOWAK B. Zur dynamischen analyse des systems stromabnehmer und fahrleitung, dargestllt am beispiel des intercity experimental[J]. VDI Berichte, 1986, (603): 245-261. [6] F· S·谢, I· E·摩尔, R· T·享克尔, 沈文钧, 张景绘. 机械振动——理论应用[M]. 北京: 国防工业出版社, 1984.181-214. [7] 翟婉明, 蔡成标. 机车-轨道耦合振动对受电弓-接触网系统动力学的影响[J]. 铁道学报, 1998, 20(1): 32-38. doi: 10.3321/j.issn:1001-8360.1998.01.005 [8] SEERING W, ARMBRUSTER K, VESELY C, et al. Experimental and analytical study of pantograph dynamics[J]. ASME Journal of Dynamics System, Measurement, and Control, 1991, 113: 242-247. doi: 10.1115/1.2896371 [9] 邢海军. 电力机车受电弓的动态特性与振动控制研究[D]. 成都: 西南交通大学, 1999. [10] 付秀通. 轮/轨-弓/网系统耦合动力学数值模拟分析与试验研究[D]. 北京: 铁道部科学研究院, 1996. [11] 张卫华. 受电弓-接触网系统动态特性的研究[D]. 成都: 西南交通大学, 1988. -
点击查看大图
计量
- 文章访问数: 555
- HTML全文浏览量: 241
- PDF下载量: 793
- 被引次数: 0
