Direct method for evaluation of wheel derailment in simulation of railway vehicle dynamics
Article Text (Baidu Translation)
-
摘要: 根据轮轨空间动态耦合关系, 提出了一种根据轮轨接触点位置进行脱轨评定的直接方法, 可用于对机车车辆动力学安全性分析评价。阐述了通过轮轨接触点进行脱轨评判的原理和采用此方法的优点。作为例子, 运用货车-轨道空间耦合模型, 对C62A货车曲线通过进行了脱轨仿真计算。仿真结果表明, 在仿真计算时采用此方法非常行之有效, 评判直观、可靠。Abstract: According to the coupling relation of wheel rail contact, a direct method is proposed to evaluate wheel derailment based on the wheel rail contact point.The advantage and the principle of the method are described. As an example, wheel derailment was simulated for a full scale freight car negotiating a curve from the point of view of vehicle track coupling dynamics.The results show that this principle is a very good method to evaluate vehicle derailment especially in simulation of railway vehicle dynamics.
-
Key words:
- railway vehicle /
- derailment /
- wheel rail contact point /
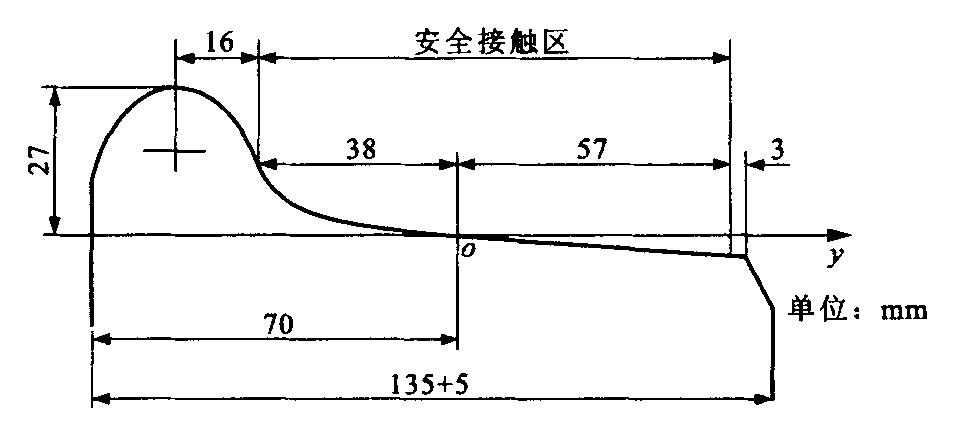
- safe contact region /
- method of evaluation
-
图 3 车辆蛇形失稳后常用脱轨指标的变化过程
Figure 3. Normal criterions for derailment after vehicle hunting motion
表 1 C62A货车空车曲线脱轨安全性指标的仿真结果
Table 1. Simulation results of criterions for derailment when a full-scale C62A freight car negotiates a curve
速度/km·h-1 轮位 脱轨系数 轮重减载率 车轮抬升量/mm 轮轨接触点/mm 左轮 右轮 左轮 右轮 左轮 右轮 左轮 右轮 40 Ⅰ 0.3390 0.3265 1.0 1.0 8.445 7.537 24.38 6.648 Ⅱ 0.3374 0.3274 1.0 1.0 3.003 2.808 -15.19 -25.91 Ⅲ 0.3281 0.3333 1.0 1.0 3.475 3.285 28.26 -13.03 Ⅳ 0.3367 0.3309 1.0 1.0 6.620 7.068 18.44 -9.091 60 Ⅰ 0.3390 0.3265 1.0 1.0 8.854 7.959 23.53 -14.49 Ⅱ 0.3374 0.3247 1.0 1.0 2.736 2.420 13.07 -18.34 Ⅲ 0.3281 0.3333 1.0 1.0 2.611 1.754 30.69 -20.07 Ⅳ 0.3307 0.3309 1.0 1.0 6.993 7.713 19.67 -10.32 85 Ⅰ 0.4501 0.3402 1.0 1.0 9.461 8.446 32.10 -31.03 Ⅱ 1.5910 1.4590 1.0 1.0 2.457 2.273 35.94 -35.44 Ⅲ 0.4224 0.3323 1.0 1.0 2.164 1.564 32.06 -20.60 Ⅳ 0.4217 0.3334 1.0 1.0 7.340 8.463 23.06 -10.32 100 Ⅰ 2.4510 0.2087 1.0 1.0 27.03 31.09 -49.40 25.13 Ⅱ 6.9260 0.3379 1.0 1.0 24.44 36.97 41.66 31.03 Ⅲ 2.1070 0.3178 1.0 1.0 12.35 8.512 38.44 -28.05 Ⅳ 0.4500 0.4152 1.0 1.0 17.53 15.16 28.86 -25.44 
下载: 导出CSV
-
[1] ZHAI Wan-ming. Vehicle -Track Coupling Dynamics (The Second Edition)[M]. Beijing: China Railway Publishing House, 2002. [2] SONG Hua. Research of wheel/rail spatially dynamic coupling relationship[D]. Chengdu: Southwest Jiaotong University, 1998. [3] WANG Kai-wen. Wheel/rail contact trochoid and the calculation of wheel/rail contact geometrical parameters[J]. Journal of Southwest Jiaotong University, 1984, 31(1): 89-98. [4] CHEN Guo. Random vibration analysis of vehicletrack coupling system[D]. Chengdu: Southwest Jiaotong University, 2000. [5] ZHAI Wan-ming, CHEN Guo. Method and criteria for evaluation of wheel derailment based on wheel vertical rise[J]. Journal of the China Railway Society, 2001, 23 (2): 17-25. -
点击查看大图
图(3) / 表(1)
计量
- 文章访问数: 403
- HTML全文浏览量: 161
- PDF下载量: 292
- 被引次数: 0
