An improvement on fuzzy comprehensive evaluation method and its use in urban traffic planning
-
摘要: 建立了一级模糊综合评价在城市重点区域交通管理规划方案评价中应用的模型, 给出相关参数的建议值, 然后结合实例对模型和参数进行了检验。针对模糊评价中指标权重确定时主观性较强的缺点, 提出一种新的方法, 结合灰关联度和熵的概念进行评价指标权重的确定, 从而使得模糊综合评价方法更加客观。将其应用于城市重点区域管理规划方案的评价, 建立了适用于区域交通管理规划方案的评价模型和算法, 并就相关参数给出了适当的建议值Abstract: For the fuzzy comprehensive evaluation method has a shortcoming that the weights of indexes usually are decided by experts, hence the conclusion is not so objective. In order to make the conclusion more objective, a new method that combines the concept of entropy and relevance rate was presented.Based on this new method, a model of evaluating traffic planning of urban key area was developed. Some values of parameters were put forward, and tested by an example.
-
Key words:
- fuzzy comprehensive evaluate method /
- traffic /
- planning /
- relevance rate /
- entropy
-
图 1 城市交通管理方案(区域方案) 综合评价指标体系
Figure 1. Comprehensive evaluation indexes system of urban traffic management planning (key area)
图 2 越大越优指标的模糊隶属函数曲线
Figure 2. The fuzzy subject function curve of more-great more-excellent index
图 3 越小越优指标的模糊隶属函数曲线
Figure 3. The fuzzy subject function curve of more-small more-excellent index
表 1 各因素评判送标准的五个分级值
Table 1. The five grades of factors
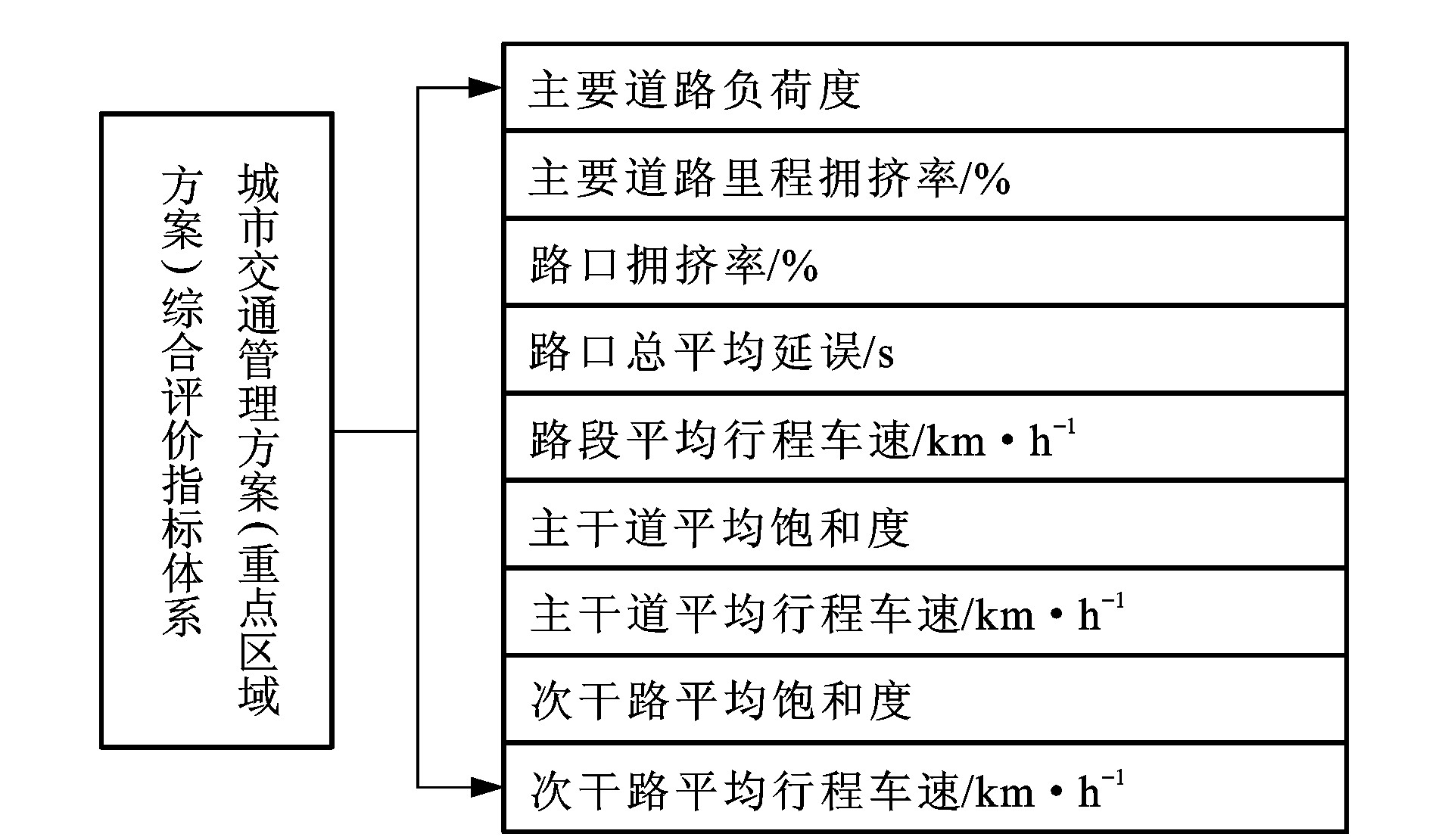
评价指标 D1 D2 D3 D4 D5 主要道路负荷度 0.50 0.55 0.65 0.75 0.85 主要道路里程拥挤率/% 15 25 35 45 55 路口拥挤率/% 10 16 22 28 34 路口总平均延误/s 35 45 55 65 75 路段总平均行程车速/km·h-1 35 28 22 15 10 主干道平均饱和度 0.4 0.5 0.6 0.7 0.8 主干道平均行程车速/km·h-1 34 31 28 25 22 次干路平均饱和度 0.25 0.30 0.35 0.40 0.45 次干路平均行程车速/km·h-1 30 25 20 15 10 
下载: 导出CSV
表 2 各方案指标值
Table 2. The original values of planning
指标 方案一 方案二 方案三(现状) 主要道路负荷度 0.53 0.55 0.66 主要道路里程拥挤率/% 9.42 17.44 48.00 路口拥挤率/% 16.67 0.00 66.67 路口总平均延误/s 21.88 16.25 48.72 路段总平均行程车速/km·h-1 30.48 27.98 19.05 主干道平均饱和度 0.53 0.49 0.62 主干道平均行程车速/km·h-1 31.35 30.03 19.37 次干路平均饱和度 0.47 0.63 0.89 次干路平均行程车速/km·h-1 26.40 21.11 17.35
下载: 导出CSV
表 3 评价指标等级量化表
Table 3. Quantities and Grades of Indexes
标准 E D C B A 得分 0~0.6 0.6~0.7 0.7~0.8 0.8~0.9 0.9~1.0
下载: 导出CSV
表 4 熵Ej和偏差度dj值
Table 4. The values of entropyEjand windbagsdj
主要道路负荷度 主要道路里程拥挤率 路口拥挤率 路口总平均延误 路段总平均行程车速 主干道平均饱和度 主干道平均行程车速 次干路平均饱和度 次干路平均行程车速 Ej 0.9967 0.95027 0.9206 0.9654 0.989 0.9966 0.9877 0.983 0.9906 dj 0.0033 0.04973 0.0794 0.0346 0.011 0.0034 0.0123 0.017 0.0094
下载: 导出CSV
-
[1] HE Ning, PAN Xiang-yang. The decision-making research on urban rapid rail transit planning[J]. China Journal of Highway and Transport, 1999, 12(3): 73-81. [2] YU Li-jun, YAN Hai, YAN Bao-jie. Maximum entropy method and it's application in probability density function of traffic flow[J]. Journal of Traffic and Transportation Engineering, 2001, 1(3): 91-94. [3] DA Qing-dong, ZHANG Guo-wu, JIANG Xue-feng. Traffic distribution and entropy[J]. Journal of Highway and Transportation Research and Development, 1999, 16(1): 37-39. [4] HAN Zheng-zhong, FANG Ning-sheng. The Application of Fuzzy Mathematics[M]. Nanjing: Southeast University Publishing Company, 1993. -
点击查看大图
计量
- 文章访问数: 282
- HTML全文浏览量: 184
- PDF下载量: 278
- 被引次数: 0
