物流运作中“啤酒游戏”的Matlab仿真

Simulation of beer game in logistics with Matlab

School of Economics and Management, Shanghai Maritime University, Shanghai 200135, China

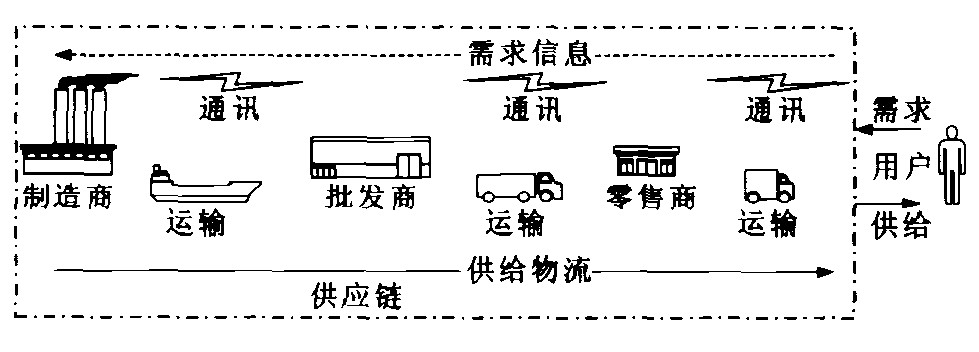
摘要: 应用Matlab/Simulink构建了“啤酒游戏”的计算机模型, 并对其进行了仿真分析。研究了订货延迟时间对物流系统库存情况造成的影响, 比较了不同采购策略对“啤酒游戏”产生的作用。发现订货延迟时间的存在是造成“啤酒游戏”中“牛鞭效应”的内因; 商家过分在意当前的库存与缺货情况, 急于补充或者降低库存, 反而会造成“牛鞭效应”的加剧与物流成本的提高。结果表明, 基于计算机技术和数学运算的Matlab/Simulink仿真技术, 是对物流系统进行科学分析的有效工具。
- 物流 /
- 仿真 /
- 啤酒游戏 /
- 牛鞭效应
Abstract: A beer game model was developed with Matlab/Simulink software, it was simulated with computer. Through this model, the influence of order delay on logistic system inventory was analyzed, the effect of different procurement plans on beer game was researched. It is pointed out that the order delay is the main reason for bullwhip effect in beer game, if sellers pay too much attention to the inventory, the bullwhip effect will be aggravated, and the logistic cost will be in-creased. The results show that the Matlab/Simulink simulation technique is efficient for analyzing logistic system.
- logistics /
- simulation /
- beer game /
- bullwhip effect

图 1 啤酒供应链

Figure 1. Supply chain of beer

下载: 全尺寸图片幻灯片

图 2 啤酒游戏模型

Figure 2. Model of beer game

下载: 全尺寸图片幻灯片

图 3 物流单元内部构造

Figure 3. Logistics units composition

下载: 全尺寸图片幻灯片

图 4 模拟结果

Figure 4. Simulation results

下载: 全尺寸图片幻灯片

图 5 A策略下的库存情况

Figure 5. A strategy inventory

下载: 全尺寸图片幻灯片

图 6 B策略下的库存情况

Figure 6. B strategy inventory

下载: 全尺寸图片幻灯片

图 7 B策略调整后的库存情况

Figure 7. Modified B strategy inventory

下载: 全尺寸图片幻灯片

[1]	[美]彼得·圣吉. 第五项修炼[M]. 上海: 生活读书新知三联书店上海分店, 2002.
[2]	王其藩. 系统动力学[M]. 北京: 清华大学出版社, 1994.
[3]	郭振宇. 中国物流现状及改善建议(一)[J]. 物流技术与应用, 2001, 6(1): 57-62. https://www.cnki.com.cn/Article/CJFDTOTAL-WLJY200101018.htm Guo Zhenyu. Current status & improvement recommendation of China's logistics (1)[J]. Logistics & Material Handling, 2001, 6(1): 57-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLJY200101018.htm
[4]	郭振宇. 中国物流现状及改善建议(二)[J]. 物流技术与应用, 2001, 6(2): 58-63. https://www.cnki.com.cn/Article/CJFDTOTAL-WLJY200102008.htm Guo Zhenyu. Current status & improvement recommendation of China's logistics (2)[J]. Logistics & Material Handling, 2001, 6(2): 58-63. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLJY200102008.htm
[5]	Simchitevi D. Designing and Managing the Supply Chain[M]. The MeGraw-Hill Companies, Inc., 2000.
[6]	杰里米夏皮罗. 供应链建模[M]. 北京: 中信出版社, 2002.
[7]	陈永春. 从Matlab/Simulink模型到代码实现[M]. 北京: 清华大学出版社, 2002.
[8]	薛定宇, 陈阳泉. 系统仿真技术与应用[M]. 北京: 清华大学出版社, 2002.