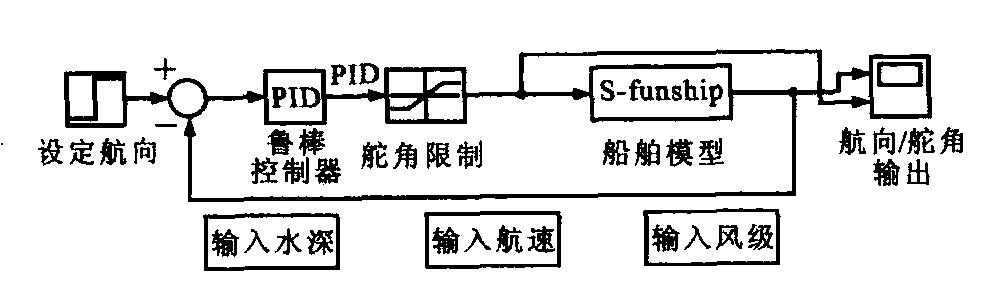
Course-keeping of inward-and-outward low speed ship
Article Text (Baidu Translation)
-
摘要: 为了在船舶进出港时, 船舶处于浅水域并以低速航行, 在风、浪等强扰动作用下, 增强航向控制性能, 减小能源损耗, 选择三阶Nomoto模型, 将航速和水深变化反映到模型参数的变化上, 基于闭环增益成形算法设计出一种具有适应性的鲁棒PID控制器, 建立基于风、浪干扰的非线性船舶运动数学模型, 并用S函数来实现。用PID控制器对非线性船舶运动数学模型进行控制, 在Simulink环境中对各种水深、船速及海况进行航向控制仿真。从仿真曲线可看出其航向跟踪效果良好, 静差为0, 且施舵合理, 所设计的控制器对非线性船舶运动数学模型具有良好的控制性能。Abstract: In order to improve ship control performance, reduce ship energy consumption when ship navigates at low speed in inward-and-outward shallow water under strong wind and wave disturbance, third-order Nomoto model was chosen, ship speed and water depth were reflected into the changes of its parameters, a robust PID controller with adaptability based on closed-loop gain shaping algorithm was designed.The nonlinear mathematical model of ship motion with wind and wave disturbance was built and realized through programming its S-function.The designed PID controller was used to control the nonlinear mathematical model of ship motion in the conditions of various water depths, ship speeds and sea states.The simulation result shows that the course-tracking effect is satisfactory, the steady state error is zero, the rudder angle is reasonable, and the designed controller has good performance for the nonlinear mathematical model.
-
表 1 Mariner轮的主要尺寸
Table 1. Main parameters of mariner ship
船长/m 160.93 舵展弦比 1.67 船宽/m 23.17 桨直径/m 6.707 吃水/m 8.23 桨螺距比 1.038 方形系数 0.588 排水量/m3 18 541 舵叶面积/m2 30.012 航速/kn 15 
下载: 导出CSV
表 2 K、T与水深的关系
Table 2. Relationship of K、T and water depth
h/d ∞ 2.50 1.93 1.50 1.21 K′ 2.386 2.848 2.449 0.957 0.234 T′1 2.749 3.244 2.678 1.072 0.231+0.153 1i T′2 0.367 0.381 0.356 0.362 0.231-0.153 1i T′3 0.729 0.788 0.585 0.477 0.277 T1+T2 3.116 3.626 3.034 1.434 0.462 T1T2 1.009 1.239 0.953 0.388 0.077
下载: 导出CSV
-
[1] 贾欣乐, 杨盐生. 船舶运动数学模型[M]. 大连: 大连海事大学出版社, 1999. [2] 贾欣乐, 张显库. 船舶运动智能控制与H∞鲁棒控制[M]. 大连: 大连海事大学出版社, 2002. [3] Zhang Xian-ku, Jia Xin-le. Simplification of H∞ mixed sensitivity algorithmandits application[J]. Automatic Control and Computer Sciences, 2002, 36(3): 28—33. [4] 张显库, 贾欣乐. 闭环增益成形算法在船舶自动舵中的应用[J]. 中国航海, 1999, 41(2): 89—93. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHH199902019.htmZhang Xian-ku, Jia Xin-le. Application of closed-loop gain shaping algorithmon autopilot for ships[J]. Navigation of China, 1999, 41(2): 89—93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHH199902019.htm [5] 张显库, 贾欣乐. 用镜像映射方法求非稳定过程的鲁棒控制器[J]. 系统工程与电子技术, 2000, 22(4): 10—12. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200004003.htmZhang Xian-ku, Jia Xin-le. Solving robust controller of unstable process using mirror-injection method[J]. Systems Engineering and Electronics, 2000, 22(4): 10—12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200004003.htm [6] 张显库, 贾欣乐. 基于闭环增益成形的鲁棒PID算法及在液位控制中的应用[J]. 中国造船, 2000, 41(3): 35—39. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC200003005.htmZhang Xian-ku, Jia Xin-le. Robust PID algorithm based on closed-loop gain shaping and its application on level control[J]. Shipbuilding of China, 2000, 41(3): 35—39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC200003005.htm [7] 张显库, 贾欣乐. 求PID参数新方法[J]. 系统工程与电子技术, 2000, 22(8): 4—5. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200008001.htmZhang Xian-ku, Jia Xin-le. A new method for solving PID Parameters[J]. Systems Engineering and Electronics, 2000, 22(8): 4—5. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200008001.htm [8] 张显库, 贾欣乐. 用闭环增益成形算法的精馏塔鲁棒控制[J]. 系统工程与电子技术, 2001, 23(5): 15—18. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200105005.htmZhang Xian-ku, Jia Xin-le. Robust control of a high purity distillation column using closed-loop gain shaping algorithm[J]. Systems Engineering and Electronics, 2001, 23(5): 15—18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD200105005.htm [9] 张显库, 张丽坤, 贾欣乐. 非方阵被控对象闭环增益成形算法及其应用[J]. 大连海事大学学报, 2001, 27(2): 63—67. https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS200102014.htmZhang Xian-ku, Zhang Li-kun, Jia Xin-le. Closed-loop gain shaping algorithm with unsquare matrix plant and its application[J]. Journal of Dalian Maritime University, 2001, 27(2): 63—67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS200102014.htm [10] 赵月林, 古文贤. 浅水低速状态下操纵运动数学模型研究[J]. 大连海运学院学报, 1993, 18(3): 242—246. https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS199203003.htmZhao Yue-lin, Gu Wen-xian. Research on mathematic ship motion model under shoal water and low speed[J]. Journal of Dalian Maritime University, 1993, 18(3): 242—246. (in Chi-nese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS199203003.htm [11] 杨盐生. 船舶运动控制研究[J]. 交通运输工程学报, 2003, 3(2): 34—39. http://transport.chd.edu.cn/article/id/200302008Yang Yan-sheng. Review on ship motion control[J]. Journal of Traffic and Transportation Engineering, 2003, 3(2): 34—39. (in Chinese) http://transport.chd.edu.cn/article/id/200302008 -
点击查看大图
图(5) / 表(2)
计量
- 文章访问数: 337
- HTML全文浏览量: 128
- PDF下载量: 279
- 被引次数: 0
