-
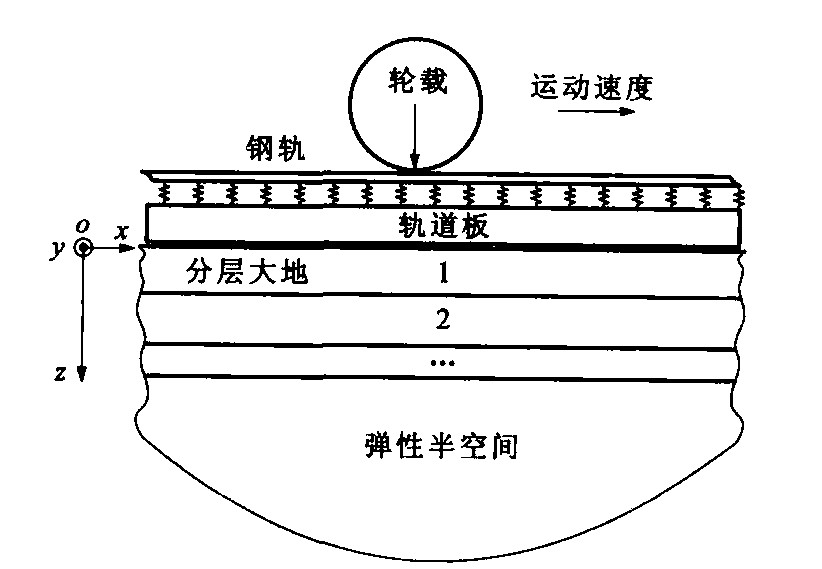
摘要: 为了研究板式轨道交通引起的地面振动, 建立了单个载荷作用下板式轨道引起的地面振动计算模型。在模型中, 考虑了板式轨道的结构特性, 大地按多层各向同性无限大弹性体建模, 其底层为弹性半空间体。对模型的动力学微分方程先在波数-频率域内进行求解, 然后利用傅立叶逆变换得到地面振动的垂向位移幅值计算表达式。算例表明, 该模型能反映出层状大地中波的频散特性, 荷载移动速度对地面振动有显著影响, 荷载速度增大, 振动响应及影响范围随之增大, 当其超过瑞利波波速时, 将会出现多普勒效应, 这说明该模型能模拟地质沉积作用下的层状大地特性。Abstract: A model was established for the study of ground vibrations generated by slab track that was subject to a unit force, the characteristics of slab track were considered, ground was modeled as a number of infinite-parallel-homogeneous-elastic layers overlying elastic half-space, the dynamic differential equations of the system were solved in wave-number domain, and then the vertical displacement amplitude of ground surface was obtained by implementing inverse Fourier transform.The applied result of the model shows that the dispersion characteristics of the vibrations propagating in ground can be demonstrated, the load speed has significant influence on ground vibrations, the spread scope and response amplitude of vibrations increase with load speed increase, Doppler effects occur when the speed is greater than Rayleigh wave speed, which indicates that the model can simulate the alluvial depositing stratification characteristics of ground.
-
Key words:
- track traffic /
- slab track /
- ground vibration /
- wave-number domain /
- vibration model
-
表 1 分层大地参数
Table 1. Layered ground parameters
层数j 厚度zj/m 杨氏模量Ej/(N·m-2) 密度ρj/(kg·m-3) 泊松比υj 损失因子ηj 1 5 30×106 1 550 0.47 0.1 无限半空间 360×106 2 000 0.49 0.1 表 2 板式轨道参数
Table 2. Slab track parameters
单位长度钢轨的质量Mr/(kg·m-1) 120 单位长度轨道板的质量Msb/(kg·m-1) 4 000 轨下支撑损失因子ηrs 0.25 轨道板的弯曲刚度EIsb/(N·m2) 1.11×108 钢轨的弯曲刚度EI/(N·m2) 6.621×107 轨下支撑刚度Krs/(N·m-2) 1.7×108 轨道和地面的接触宽度B/m 2.4 轨道板的损失因子ηsb 0.03 -
[1] 江岛淳. 地盘振动と对策—基础. 法令から交通. 建设振动まで[M]. 东京: 吉井书店, 1982. [2] Takemiya H. Simulation of track-ground vibrations due to a high-speed train: the case of X-2000 at Ledsgard[J]. Journal of Sound and Vibration, 2003, 261(3): 503-526. doi: 10.1016/S0022-460X(02)01007-6 [3] Yang Y B, Hung H H, Chang D W. Train-induced wave propagationin layered soils using finite/infinite element simulation[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(4): 263-278. doi: 10.1016/S0267-7261(03)00003-4 [4] Antes H, Von Estorff O. Dynamic response analysis of rigid foundations and of elastic structures by boundary element procedures[J]. Soil Dynamics and Earthquack Engineering, 1989, 8(2): 68-74. doi: 10.1016/S0267-7261(89)80014-4 [5] Sheng X, Jones CJ C, Petyt M. Ground vibration generated by a harmonic load acting on a railwaytrack[J]. Journal of Soundand Vibration, 1999, 225(1): 3-28. doi: 10.1006/jsvi.1999.2232 [6] Sheng X, Jones CJ C, Petyt M. Ground vibration generated by a load moving along a railway track[J]. Journal of Sound and Vibration, 1999, 228(1): 129-156. doi: 10.1006/jsvi.1999.2406 [7] 徐志胜, 翟婉明. 轨道交通轮轨噪声预测模型[J]. 交通运输工程学报, 2005, 5(3): 14-18. http://transport.chd.edu.cn/article/id/200503004Xu Zhi-sheng, Zhai Wan-ming. Prediction model of wheel-rail noise for rail transit[J]. Journal of Traffic and Transportation Engineering, 2005, 5(3): 14-18. (in Chinese) http://transport.chd.edu.cn/article/id/200503004 [8] 王逢朝, 夏禾, 吴萱. 列车振动对环境及建筑物的影响分析[J]. 北方交通大学学报, 1999, 23(4): 13-17. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT904.003.htmWang Feng-chao, Xia He, Wu Xuan. Vibration effects of trains on surrounding environments and buildings[J]. Journal of Northern Jiaotong University, 1999, 23(4): 13-17. (in Chi-nese). https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT904.003.htm [9] 夏禾, 张楠, 曹艳梅. 列车对周围地面及建筑物振动影响试验研究[J]. 铁道学报, 2004, 26(4): 93-98. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200404020.htmXia He, Zhang Nan, Cao Yan-mei. Experimental study of train-induced vibrations of ground and nearby buildings[J]. Journal of the China Railway Society, 2004, 26(4): 93-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200404020.htm [10] 蒋通, 张昕. 高架轨道交通引起环境振动实测与数值模拟[J]. 同济大学学报: 自然科学版, 2004, 23(5): 566-569. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200405001.htmJiang Tong, Zhang Xin. In situs Experimental and numerical predictions of environmental vibration by urban viaduct rail transit[J]. Journal of Tongji University: Natural Science, 2004, 23(5): 566-569. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200405001.htm [11] 何华武. 无碴轨道技术[M]. 北京: 中国铁道出版社, 2005. [12] 雷晓燕, 圣小珍. 铁路交通噪声与振动[M]. 北京: 科学出版社, 2004. -





 下载:
下载: