高速公路意外事件影响下的车辆跟驰模型

陈斌; 魏朗

高速公路意外事件影响下的车辆跟驰模型

陈斌^1,,
魏朗²

1.
四川交通职业技术学院汽车工程系，四川成都 611130
2.
长安大学汽车学院，陕西西安 710064

基金项目:

四川交通科技项目 2003-0710A

四川交通优秀教师科技项目 2003-U491-01Z

详细信息

作者简介:
陈斌(1973-)，男，四川中江人，四川交通职业技术学院副教授，工学博士，从事交通信息工程及控制研究

中图分类号: U491.255
计量
- 文章访问数: 358
- HTML全文浏览量: 110
- PDF下载量: 275
- 被引次数: 0
出版历程
- 收稿日期: 2005-12-16
- 刊出日期: 2006-09-25

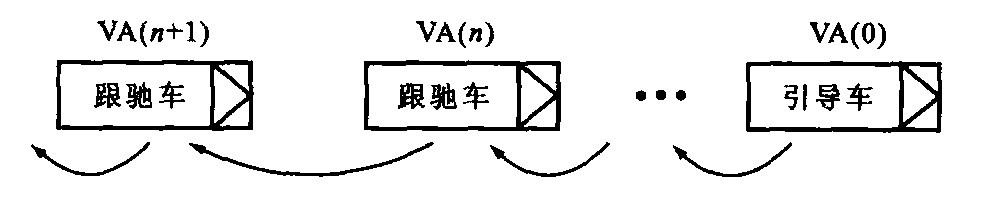
Car-following model under influence of expressway accident

CHEN Bin^1
,,
WEI Lang²

1.
Department of Automobile Engineering, Sichuan Vocational and Technical College of Communications, Chengdu 611130, Sichuan, China
2.
School of Automobile, Chang'an University, Xi'an 710064, Shaanxi, China

More Information

Author Bio:
Chen Bin(1973-), male, PhD, associate professor, 86-28-82680060, cbll03@tom.com

Article Text (Baidu Translation)

摘要

摘要: 应用智能主体技术, 针对双向四车道高速公路意外事件影响下的车辆跟驰行为, 建立了基于智能主体的车辆跟驰模型, 利用西部高速公路交通调查统计的数据, 对车辆主体的间距愿望进行了定量分析, 利用比例微分控制确定车辆主体的加速度响应, 建立了不同加速度队列的逻辑意图, 使模型的加速度响应符合车辆的动力特性。利用开发的EAD-Simulation系统, 在特定和随机两种不同过程下对模型进行的测试表明: 利用智能主体技术描述高速公路意外事件影响下的跟驰行为, 可充分发挥其个性、自治性和自适应性的特点, 在主体的属性描述中利用比例微分控制“类阻尼”的特性, 可有效地对车辆主体的稳定性进行控制。
- 交通工程 /
- 跟驰模型 /
- 智能主体 /
- 意外事件
Abstract: With agent technology and in view of car-following behavior under the influence of accidents happening on bidirectional four-carriageway expressway, a car-following model based on agent was established.In the description of vehicle agent properties, the quantitative analysis of its separation-desire was carried out according to the data of West China expressway traffic surveys and statistics, the acceleration of vehicle agent was determined by proportional-derivative control theory, the logic intention queue with different accelerations was set up, which made the acceleration response of the model comply with vehicle dynamic features.The model was tested both under specified condition and in random process according to EAD-simulation system.Test result shows that the model can represent the individuality, self-constraint characteristic and self-adaptability of vehicle agent, control its stability by the similar damped character of proportional-derivative control.
- traffic engineering /
- car-following model /
- agent /
- accident

HTML全文

图 1 跟驰框架

Figure 1. Fallowing framework

下载: 全尺寸图片幻灯片

图 2 车辆主体结构

Figure 2. Structure of vehicle agent

下载: 全尺寸图片幻灯片

图 3 意图决策的逻辑流程

Figure 3. Logic program of intention decision

下载: 全尺寸图片幻灯片

图 4 间距愿望与当前速度关系

Figure 4. Relationship of separation-desire and velocity

下载: 全尺寸图片幻灯片

图 5 反馈控制系统

Figure 5. Feedback control system

下载: 全尺寸图片幻灯片

图 6 R_rv和R_rd关系

Figure 6. Relationship of R_rv and R_rd

下载: 全尺寸图片幻灯片

图 7 车辆跟驰模型性能对比

Figure 7. Property comparison of car-following models

下载: 全尺寸图片幻灯片

图 8 车辆跟驰特性

Figure 8. Characteristics of car-following model

下载: 全尺寸图片幻灯片

参考文献(8)

[1]	陈斌. 高速公路意外事件下的车辆行为模型与事件检测研究[D]. 成都: 西南交通大学, 2005.
[2]	陈斌, 金炜东, 高利. 特殊过程下的车辆跟驰模型数值模拟分析[J]. 中国公路学报, 2005, 18 (1): 90-94. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200501020.htm Chen Bin, Jin Wei-dong, Gao Li. Numerical simulation and analysis of car-following models in particular progress[J]. China Journal of Highway and Transport, 2005, 18 (1): 90-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200501020.htm
[3]	杨佩昆. 智能交通运输系统体系结构[M]. 上海: 同济大学出版社, 2001.
[4]	Hilaire V, Koukam A, Gruer P. Multi-agent approach to modeling and simulation of urban transportation systems[A]∥Proceedings of the IEEEInternational Conference on Systems, Man and Cybernetics[C]. Tucson: IEEE Press, 2001.
[5]	王震宇, 高更君, 黄卫. 基于多智能主体的高速公路控制系统结构[J]. 交通运输工程学报, 2003, 3 (1): 76-79. http://transport.chd.edu.cn/article/id/200301017 Wang Zhen-yu, Gao Geng-jun, Huang Wei. Architecture of expressway traffic control systembased on multi-agent[J]. Journal of Traffic and Transportation Engineering, 2003, 3 (1): 76-79. (in Chinese) http://transport.chd.edu.cn/article/id/200301017
[6]	陈斌. 基于多智能主体系统的车道变换模型[J]. 中国公路学报, 2005, 18 (3): 104-108. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200503022.htm Chen Bin. Lane-changing model based on multi-agent system[J]. China Journal of Highway and Transport, 2005, 18 (3): 104-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200503022.htm
[7]	贾鸿飞, 隽志才. 基于期望间距的车辆跟驰模型的建立[J]. 中国公路学报, 2000, 13 (4): 86-87. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200004019.htm Jia Hong-fei, Juan Zhi-cai. Development of a car-following model based on desired spacing[J]. China Journal of Highway and Transport, 2000, 13 (4): 86-87. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200004019.htm
[8]	徐薇莉, 曹柱中. 自动控制理论与设计[M]. 上海: 上海交通大学出版社, 2001.