Increment feedback control algorithm of ship track based on nonlinear sliding mode
Article Text (Baidu Translation)
-
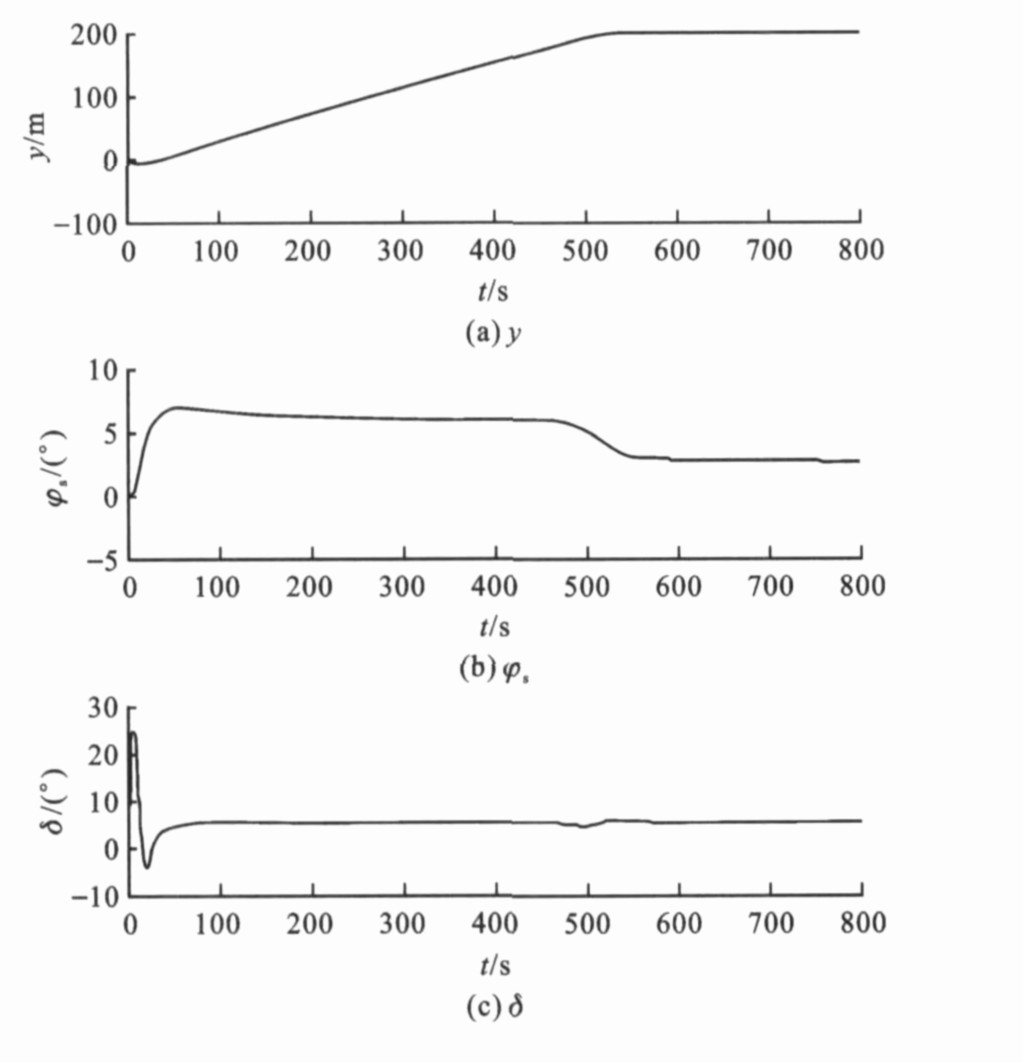
摘要: 分析了带有状态变量及控制输入约束条件的欠驱动船舶航迹控制问题, 结合增量反馈技术, 对控制系统输出进行动态非线性滑动模态分解迭代设计, 提出了一种基于分解迭代非线性滑模的船舶航迹增量反馈控制方法, 以避免定常干扰引起的稳态误差及变结构控制的抖振问题, 无需对不确定风、流干扰以及模型参数进行估计, 能够同时稳定船舶的航向和航迹。应用“育龙”轮的系统模型进行了仿真, 结果表明, 控制器对系统参数摄动及外界干扰不敏感, 具有强的鲁棒性, 且其设计参数物理意义明显, 易于调节。Abstract: The straight-path tracking problem of underactuated ship with state constraints and actuator saturation was analysed, a nonlinear control algorithm was developed by integrating increment feedback and dynamic nonlinear sliding mode based on an iterative designing procedure, so that the problems of static error caused by constant disturbances and chattering in variable structure control were circumvented, the heading and the cross-track error of ship were stabilized without necessary estimating the parametric uncertainties and disturbances induced by wind and current.Numerical simulation result of training ship "Yulong" shows that the controller is robust to systemic variation or outside disturbances and easy to adjust due to the clearness of parametric functions.
-
Key words:
- ship engineering /
- track control /
- nonlinear sliding mode /
- increment feedback
-
[1] Fossen T I. Marine Control Systems-Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles[M]. Trondheim: Norwegian University of Science and Technology, 2002. [2] Pettersen K Y, Lefeber E. Way-point tracking control of ships[A]// Proceedings of the 40th IEEE Conference on Decision and Control[C]. Orlando: IEEE CNF, 2001. [3] Do K D, Pan J. Global waypoint tracking control of underactuated ships under relaxed assumptions[A]// Proceedings of the 42nd IEEE Conference on Decision and Control[C]. Maui: IEEE CNF, 2003. [4] Michele A, Giuseppe C, Giovanni I, et al. A planar path following controller for underactuated marine vehicles[A]// The 9th IEEE Conference on Control and Automation[C]. Dubrovnik: IEEE CNF, 2001. [5] Han Bing, Zhao Guo-liang. Path tracking control of underactuated surface vessels based on the differential flatness[J]. Journal of Harbin Engineering University, 2004, 25(6): 709-713. [6] 李铁山, 杨盐生, 郑云峰. 不完全驱动船舶非线性控制[J]. 交通运输工程学报, 2003, 3(4): 39-43. doi: 10.3321/j.issn:1671-1637.2003.04.010Li Tie-shan, Yang Yan-sheng, Zheng Yun-feng. Nonlinear control of underactuated ships[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4): 39-43. (in Chinese) doi: 10.3321/j.issn:1671-1637.2003.04.010 [7] 李铁山, 杨盐生, 郑云峰. 不完全驱动船舶航迹控制输入输出线性化设计[J]. 系统工程与电子技术, 2004, 26(7): 945-948. doi: 10.3321/j.issn:1001-506X.2004.07.025Li Tie-shan, Yang Yan-sheng, Zheng Yun-feng. Input-output linearization designs for straight-line tracking control of underactuated ships[J]. Systems Engineering and Electronics, 2004, 26(7): 945-948. (in Chinese) doi: 10.3321/j.issn:1001-506X.2004.07.025 [8] 李铁山, 杨盐生. 基于耗散理论的不完全驱动船舶直线航迹控制设计[J]. 应用科学学报, 2005, 23(2): 204-208. doi: 10.3969/j.issn.0255-8297.2005.02.021Li Tie-shan, Yang Yan-sheng. A robust design based on the dissipation theory for the linear course trajectory control of underactuated ships[J]. Journal of Applied Sciences, 2005, 23(2): 204-208. (in Chinese) doi: 10.3969/j.issn.0255-8297.2005.02.021 [9] Michael G P, Ailan C C, Cao Yu-song. An assessment of fuzzy logic vessel path control[J]. IEEE Journal of Oceanic Engineering, 1995, 20(4): 276-284. doi: 10.1109/48.468247 [10] Zhang Yao, Grant E H, Pratyush S. A neural approach to ship track-keeping control[J]. IEEE Journal of Oceanic Engineering, 1996, 21(4): 513-527. -





 下载:
下载: