-
摘要: 为了克服单一的交通流预测模型性能不稳定的问题, 提出了基于约束卡尔曼滤波的短时交通流量组合预测模型。约束卡尔曼滤波组合预测模型以各单一预测模型的权重为状态变量, 交通流量为观测变量, 预测结果是单一预测模型的加权和, 加权系数由约束卡尔曼滤波方程递推动态确定, 最后通过广深高速公路上采集的交通流量数据对算法进行了验证。结果表明, 在不同预测步长情况下, 约束卡尔曼滤波组合预测模型要优于最佳的单一预测模型或与其持平, 并且不受某一较差的预测模型影响, 具有较高的鲁棒性。Abstract: In order to avoid the unstableness of single traffic flow prediction model, a constrained Kalman filter combined(CKFC) predictor was proposed for short-term traffic flow, the weight of each single predictor was used as state variable for the predictor, traffic flow was used as measurement variable, CKFC predictor's result was a weighted sum of single predictor, the weights were decided by constrained Kalman filter dynamically, and CKFC predictor was tested using traffic flow data collected on Guangshen freeway.Analysis result indicates that CKFC predictor is better than or at least as good as the optimum single predictor, it is not influenced by poor predictor and has high robustness.
-
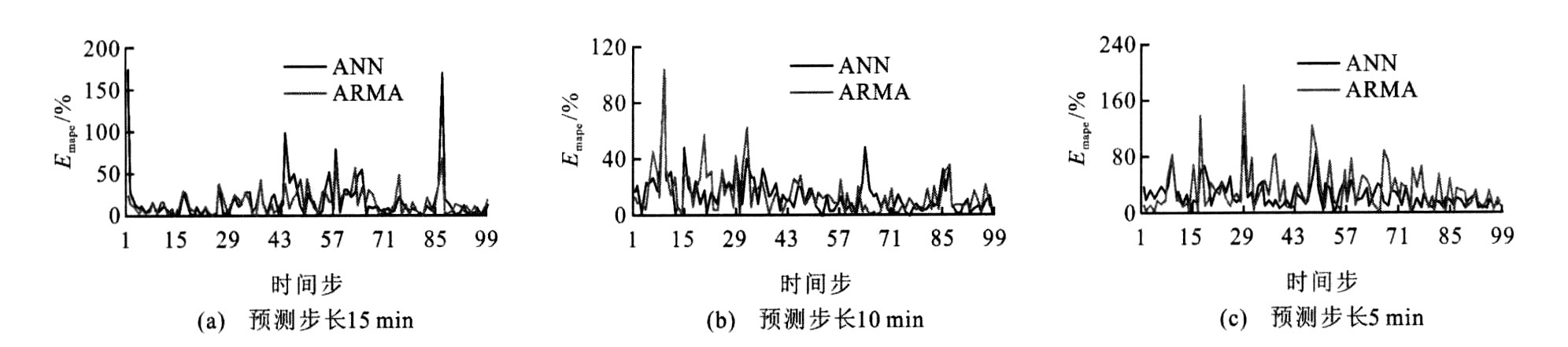
表 1 无噪声情况下3种预测方法性能对比
Table 1. Performance comparison among three predictors for noise-free data
模型 5 min间隔数据 10 min间隔数据 15 min间隔数据 Emape/% Eec Emape/% Eec Emape/% Eec ANN 18.2 0.920 14.0 0.930 17.5 0.927 ARMA 24.3 0.906 16.8 0.926 16.2 0.927 CKFC 18.3 0.925 14.0 0.936 15.8 0.930 
下载: 导出CSV
表 2 有噪声情况下3种预测方法性能对比
Table 2. Performance comparison among three predictors for noise data
模型 5 min间隔数据 10 min间隔数据 15 min间隔数据 Emape/% Eec Emape/% Eec Emape/% Eec ANN 18.2 0.920 14.0 0.930 17.5 0.927 ARMA 24.3 0.906 16.8 0.926 16.2 0.927 模拟预测 39.7 0.796 38.0 0.801 37.7 0.774 CKFC 16.9 0.929 13.8 0.936 15.2 0.927
下载: 导出CSV
-
[1] WILLI AMS B M, DURVASULA P K, BROWN D E. Urban freeway traffic flowprediction: application of seasonal autoregressive integrated moving average and exponential smoothing models[R]. Washington DC: Transportation Research Record 1644, 1998. [2] OKUTANI I, STEPHANEDES Y J. Dynamic prediction of traffic volume through Kal man filtering theory[J]. Transportation Research Part B, 1984, 18(1): 1-11. doi: 10.1016/0191-2615(84)90002-X [3] DAVIS G A, NI HAN N L. Nonparametric regression and short termfreeway traffic forecasting[J]. Journal of Transportation Engineering, 1991, 117(2): 178-188. doi: 10.1061/(ASCE)0733-947X(1991)117:2(178) [4] SMITHB L, DEMETSKY MJ. Short-termtraffic flow prediction: neural network approach[R]. Washington DC: Transportation Research Record 1453, 1994. [5] 刘静, 关伟. 交通流预测方法综述[J]. 公路交通科技, 2004, 21(3): 82-85. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK2020S1025.htmLI UJing, GUAN Wei. Asummary of traffic flowforecastin gmethods[J]. Journal of Highway and Transportation Research and Development, 2004, 21(3): 82-85. (in Chi-nese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK2020S1025.htm [6] 郑为中, 史其信. 基于贝叶斯组合模型的短期交通量预测研究[J]. 中国公路学报, 2005, 18(1): 85-89. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200501019.htmZHENG Wei-zhong, SHI Qi-xin. Study of short-termfreeway traffic flow prediction based on Bayesian combined model[J]. China Journal of Highway and Transport, 2005, 18(1): 85-89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200501019.htm [7] ANDERSON B, MOORE J. Opti mal Filtering[M]. New Jersey: Prentice Hall, 1979. [8] SI MON D, SI MON D L. Kal man filtering with inequality constraints for turbofan engine health esti mation[J]. Control Theory and Applications, IEE Proceedings, 2006, 153(3): 371-378. doi: 10.1049/ip-cta:20050074 [9] SI MON D, CHI A T L. Kal man filtering with state equality constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 128-136. https://ieeexplore.ieee.org/document/993234 [10] 何兆成, 余志. 城市道路网络动态OD估计模型[J]. 交通运输工程学报, 2005, 5(2): 94-98. http://transport.chd.edu.cn/article/id/200502023HE Zhao-cheng, YU Zhi. Dynamic OD esti mation model of urban network[J]. Journal of Traffic and Transportation Engineering, 2005, 5(2): 94-98. (in Chinese) http://transport.chd.edu.cn/article/id/200502023 -
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 323
- HTML全文浏览量: 127
- PDF下载量: 479
- 被引次数: 0
