Reserve depot location of railway emergency material
Article Text (Baidu Translation)
-
摘要: 为求解满足应急时间约束及数量最少的铁路应急物资储备点选址问题, 分析了铁路应急物资储备点选址问题的独特性, 将复杂的铁路路网简化为路段, 依托供需可达矩阵建立数学模型, 结合改进的分支剪支搜索方法给出了求解程序, 并以某铁路局的应急物资储备点选址问题为例进行了实证分析。分析结果表明: 选取阎良作为防洪物资储备点符合实际情况, 该模型能够在保证有效解一致的前提下, 将复杂的铁路路网简化为路段, 消除了点覆盖线的约束, 适用于铁路应急物资储备点选址问题。Abstract: In order to solve the reserve depot location problem of railway emergency material with the restrictions of response time and minimum number of reserve depots, complex railway network was simplified to sections by analyzing the uniqueness of the problem. A mathematic model was established relying on supply and demand matrix, and its solving program with improved branch and cut search method was introduced. The reserve depot location problem of a railway bureau was taken as an empirical analysis. Analysis result indicates that choosing Yanliang as reserve depot is correspond to reality, the model simplifies complex railway network to sections with the premise of ensuring the consistency of effective solution, and eliminates the constraint of point covering line, so the model is more applicable to the reserve depot location problem of railway emergency material.
-
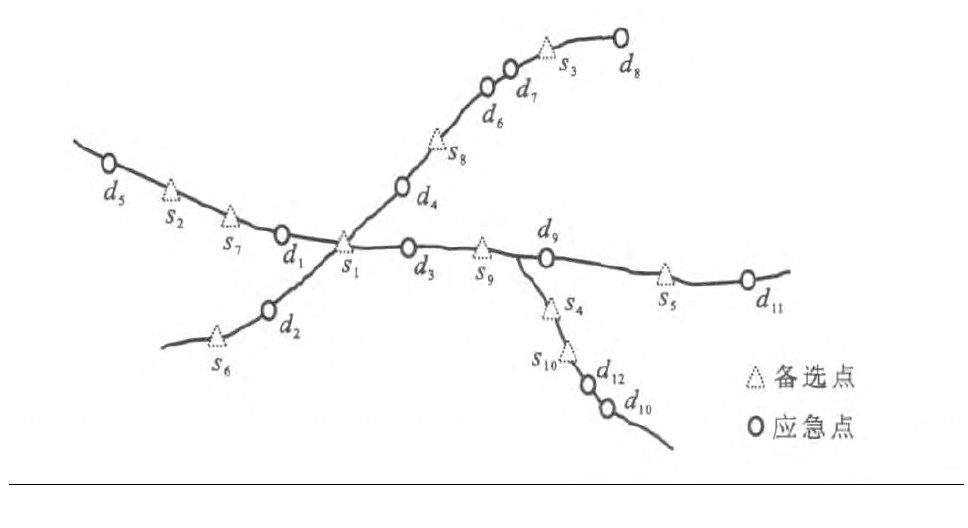
表 1 备选点与应急点之间的距离
Table 1. Distances between alternative reserve depots and emergency depots

-
[1] 李卫军, 王娟, 马剑. 城市轨道交通网络化应急抢险资源优化配置[J]. 现代城市轨道交通, 2009 (4): 9-13. doi: 10.3969/j.issn.1672-7533.2009.04.004LI Wei-jun, WANG Juan, MA Jian. Optimal allocation of emergency resource for urban rail transit network[J]. Modern Urban Transit, 2009 (4): 9-13. (in Chinese) doi: 10.3969/j.issn.1672-7533.2009.04.004 [2] 濮居一, 柴干. 高速公路应急系统单救援服务点选址问题研究[C]∥中国人工智能学会. 第一届智能交通与人工智能学术研讨会论文集. 广州: 中国人工智能学会, 2006: 223-226.PU Ju-yi, CHAI Gan. A study on single rescue facility location problemof freeway emergency system[C]∥Chinese Association for Artificial Intelligence. Collected Papers of First Symposium on Intelligent Transportation and Artificial Intelligence. Guangzhou: Chinese Association for Artificial Intelligence, 2006: 223-226. (in Chinese) [3] 金卓. 高速公路养护站点布设及设备配置研究[D]. 西安: 长安大学, 2009.JI N Zhuo. The study on maintenance site distribution and device configuration of expressway[D]. Xi'an: Chang' an University, 2009. (in Chinese) [4] 向红艳, 邵毅明, 王亮亮. 高速公路应急救助的资源规划选址模型[J]. 科学技术与工程, 2009, 9 (10): 2655-2658. doi: 10.3969/j.issn.1671-1815.2009.10.024XI ANG Hong-yan, SHAO Yi-ming, WANG Liang-liang. Resource distribution model for expressway emergencyrescue[J]. Science Technology and Engineering, 2009, 9 (10): 2655-2658. (in Chinese) doi: 10.3969/j.issn.1671-1815.2009.10.024 [5] 蔡文学, 宋尚江. 考虑最大弧段覆盖连续衰退的危险品运输应急选址问题[J]. 物流技术, 2010, 29 (4): 68-70. doi: 10.3969/j.issn.1005-152X.2010.08.023CAI Wen-xue, SONG Shang-jiang. Maximum arc-covering continuous decay-considered emergency allocation of hazardous materials transportation[J]. Logistics Technology, 2010, 29 (4): 68-70. (in Chinese) doi: 10.3969/j.issn.1005-152X.2010.08.023 [6] 王文峰, 郭波, 刘新亮. 多级覆盖设施选址问题建模及求解方法研究[J]. 中国管理科学, 2007, 15 (增): 144-148. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZHYJ200710001032.htmWANG Wen-feng, GUO Bo, LIU Xin-liang. Model and solution approach for multiple-quality-of-coverage facility location problem[J]. Chinese Journal of Management Science, 2007, 15 (S): 144-148. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZHYJ200710001032.htm [7] 方磊, 何建敏. 综合AHP和目标规划方法的应急系统选址规划模型[J]. 系统工程理论与实践, 2003, 23 (12): 116-120. doi: 10.3321/j.issn:1000-6788.2003.12.019FANG Lei, HE Jian-min. Combining the analytic hierarchy process and goal programming for location model of emergency systems[J]. Systems Engineering—Theory and Practice, 2003, 23 (12): 116-120. (in Chinese) doi: 10.3321/j.issn:1000-6788.2003.12.019 [8] 张静, 刘茂. 广义最大覆盖模型在消防站优化选址中的应用[J]. 安全与环境学报, 2009, 9 (1): 169-172. doi: 10.3969/j.issn.1009-6094.2009.01.046ZHANG Jing, LIU Mao. Application of the general maximum covering model tothelocality choice of fire stations[J]. Journal of Safety and Environment, 2009, 9 (1): 169-172. (in Chinese) doi: 10.3969/j.issn.1009-6094.2009.01.046 [9] 于瑛英, 池宏, 祁明亮, 等. 应急管理中资源布局评估与调整的模型和算法[J]. 系统工程, 2008, 26 (2): 75-81. doi: 10.3969/j.issn.1009-6744.2008.02.012YU Ying-ying, CHI Hong, QI Ming-liang, et al. Modelling and algorithm of resource location and allocation assessment and adjustment in emergency management[J]. Systems Engineering, 2008, 26 (2): 75-81. (in Chinese) doi: 10.3969/j.issn.1009-6744.2008.02.012 [10] 赵远飞, 陈国华. 基于改进逼近理想解排序(TOPSIS) 法的应急系统优化选址模型研究[J]. 中国安全科学学报, 2008, 18 (9): 22-28. doi: 10.3969/j.issn.1003-3033.2008.09.004ZHAO Yuan-fei, CHEN Guo-hua. Study on location optimizing model of emergency system based on improved TOPSIS method[J]. China Safety Science Journal, 2008, 18 (9): 22-28. (in Chinese) doi: 10.3969/j.issn.1003-3033.2008.09.004 [11] 方磊, 何建敏. 城市应急系统优化选址决策模型和算法[J]. 管理科学学报, 2005, 8 (1): 12-16. doi: 10.3321/j.issn:1007-9807.2005.01.003FANG Lei, HE Jian-min. Optimal location model and algorithm of urban emergency systems[J]. Journal of Management Sciences in China, 2005, 8 (1): 12-16. (in Chinese) doi: 10.3321/j.issn:1007-9807.2005.01.003 [12] 张玲, 黄钧, 朱建明. 应对大规模突发事件的资源布局模型与算法[J]. 系统工程, 2008, 26 (9): 26-31. doi: 10.3969/j.issn.1001-4098.2008.09.005ZHANG Ling, HUANG Jun, ZHU Jian-ming. Thelocation and allocation model and algorithm of response to large-scale emergency[J]. Systems Engineering, 2008, 26 (9): 26-31. (in Chinese) doi: 10.3969/j.issn.1001-4098.2008.09.005 [13] 王炜, 刘茂. 多阶段优化规划模型在天津应急资源基站优化规划中的应用[J]. 安全与环境学报, 2009, 9 (1): 164-168. https://www.cnki.com.cn/Article/CJFDTOTAL-AQHJ200901046.htmWANG Wei, LIU Mao. Multi-stagedlocation-choosing model for optimizing the location-choice of the emergency resource depots in Tianjin[J]. Journal of Safety and Environment, 2009, 9 (1): 164-168. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-AQHJ200901046.htm [14] BERMAN O, KRASS D, DREZNER Z. The gradual covering decay location problemon a network[J]. European Journal of Operational Research, 2003, 151 (3): 474-480. doi: 10.1016/S0377-2217(02)00604-5 [15] 汪定伟, 张国祥. 突发性灾害救援中心选址优化的模型与算法[J]. 东北大学学报: 自然科学版, 2005, 26 (10): 953-956. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX200510009.htmWANG Ding-wei, ZHANG Guo-xiang. Model and algorithm to optimize location of catastrophic rescue center[J]. Journal of Northeastern University: Natural Science, 2005, 26 (10): 953-956. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX200510009.htm -





 下载:
下载: