Loading test and finite element analysis on convex steel box section of arch rib
-
摘要: 以宁波市东外环甬江大桥凸形钢箱拱肋截面为对象, 应用预应力钢绞线的自平衡加载方式进行了1∶4的拱肋节段缩尺模型荷载试验, 采用板壳单元和实体单元建立了有限元模型, 进行了非线性分析, 研究了考虑初始缺陷和局部屈曲的凸形钢箱拱肋截面的受力特性、实际承载能力和局部失稳机理。研究结果表明: 各测点实测应力与截面平均应力较接近, 根据测点实测应力与截面平均应力之间的关系可将凸形截面分成4类测点; 有限元所得应力与实测应力趋势相同, 数值相近; 凸形钢箱拱肋截面的强度折减系数为0.94~0.98;纵向加劲肋和横隔板结构能有效防止凸形截面加劲板件的局部屈曲; 在极限荷载作用下节段出现了凹凸的波节, 由于各加劲板出平面位移过大而导致无法继续承载。Abstract: The convex steel box section of arch rib for Yongjiang Bridge in East Outer Ring Road of Ningbo City was taken as object, the 1/4 scale-model loading experiment of arch rib segment was conducted by using the self-balanced loading mode of prestressed steel strand. A finite element model was built based on shell and solid elements, and nonlinear analysis was carried out. The mechanical characteristic, actual bearing capacity and local instability mechanism of convex steel box section of arch rib were studied considering initial imperfections and local buckling. Analysis result shows that the measured stress of each measurement point is close to section average stress, and measurement points can be categorized into four kinds according to the relationship between measured stress and section average stress. The stresses from experiment and finite element analysis show the same tendency and similar value. The strength reduction coefficient of convex steel box section of arch rib is 0.94-0.98. The local buckling of stiffened plate can be prevented effectively by longitudinal stiffeners and diaphragms. Segment has wave shape under ultimate load, and fails to resist applied load due to the larger out-of-plate deformation of each stiffened plate. 1 tab, 18 figs, 12 refs.
-
0. 引言
随着钢桥理论的发展及钢材质量等级的提高，钢拱桥的跨径逐渐向大跨径方向发展。近几年来，作为大跨度桥梁主要形式之一的钢箱拱桥得到了迅速发展。现已建成的较大跨度的钢箱拱桥有：2002年建成的主跨130 m的云南小湾大桥，是中国首座中承式钢箱提篮拱桥；2003年建成的主跨550 m的卢浦大桥，是当今世界上跨度最大的钢箱拱桥；2004年建成的主跨208 m的厦门纳潮口大桥，是中国首座海上钢箱提篮拱桥；2007年建成的的主跨420 m的重庆菜园坝大桥，是中国第一座特大公轨两用钢箱提篮拱桥；2010年建成的主跨300 m的广西南宁大桥，是中国第一座大跨径的异形钢箱拱桥[1]。以上有代表性的钢拱桥中除卢浦大桥外均为单肢钢箱拱，即钢箱拱肋为单箱，这种标准截面的单箱钢拱的经验积累较为丰富，设计计算较为成熟。
目前建成的宁波东外环甬江大桥（明州大桥）的主拱拱肋是由上下肢组成的双肢钢箱拱肋，它与卢浦大桥的矩形钢箱和倒梯形钢箱组成的陀螺形拱肋截面有所区别，其拱肋在跨中区域以外，上下肢分开，各自独立，在以主拱跨中为中心的315 m节段内，上下肢矩形钢箱结合成一凸形截面。该凸形截面形式新颖，在国内外大跨度钢拱桥中很少采用这种截面形式，可借鉴的工程实例非常少。该桥在截面设计时，采用日本道路协会出版的《道路桥示方书· 同解说Ⅰ共通篇Ⅱ钢桥篇》（以下简称《道路桥示方书》）中标准箱形截面的加劲肋设计和抗压强度标准来设计凸形截面的加劲肋，并定义截面抗压强度，以确保该凸形截面各板件的局部稳定。但是，由于该凸形截面不同于标准箱形截面，目前国内外还没有规范对这种凸形钢箱截面的加劲肋设计和考虑局部屈曲的抗压强度做出相应的规定，同时对于非规则的钢箱截面的研究，只发现日本的足立正和等对八角形柱的极限承载力进行过参数分析[2]。
本文以宁波市东外环甬江大桥凸形拱肋截面为研究对象，进行了1∶4拱肋节段缩尺模型试验，并结合非线性有限元分析，研究该凸形钢箱拱肋截面的受力特性、实际承载能力和局部失稳机理。
1. 工程概况
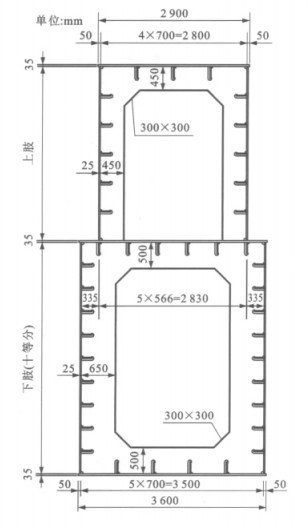
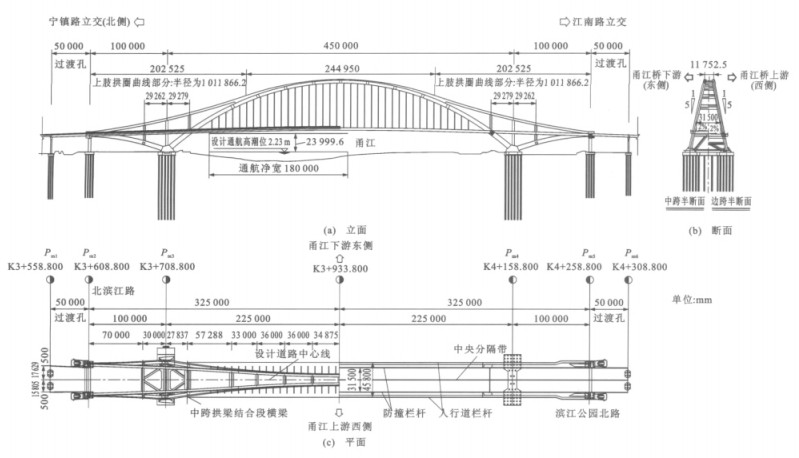
宁波市东外环甬江大桥主桥采用双肢中承式钢箱系杆拱桥，跨径布置为100 m+450 m+100 m，主桥桥面竖曲线半径R为4500 m，主桥桥面宽度为45.8 m，总体布置见图 1。边跨拱肋与中跨拱肋保持在一个平面内，横向倾斜度为1∶5。拱肋分为上下两肢，边跨下肢拱采用二次抛物线，净矢高为4.5 m；主跨下肢拱采用悬链线，矢跨比为1/5，拱轴系数为1.6；上肢拱采用两端圆曲线和中间二次抛物线组合，中间二次抛物线部分矢跨比为1/11.5。主跨下肢拱截面宽度为3.5 m，截面高度从拱座处的6.5 m变至拱顶处上下肢结合的凸形截面的4.8 m，顶、底板厚度为30~55 mm，腹板厚度为25~30 mm；边拱下肢拱截面宽度为3.5 m，截面高度从拱座处的6.0 m变至尾端处5.0 m，顶、底板厚度为30~35 mm，腹板厚度为20~30 mm；上肢拱截面宽度为2.8 m，高度为3.0 m，顶、底板厚度为16~20 mm，腹板厚度16~20 mm。在以主拱跨中为中心的315 m节段内，上下肢结合成一凸形截面，见图 2[3-6]。
凸形钢箱拱肋截面设计时，采用《道路桥示方书》中的相关规定。该规范采用容许应力设计方法，同时规定加劲肋的最小刚度比和面积比，使受压加劲肋板件整体、局部屈曲系数相等。受压加劲板件的容许应力为
$$ \sigma_{\mathrm{ca}}=\sigma_{\mathrm{cag}} \sigma_{\mathrm{cal}} / \sigma_{\mathrm{cao}} $$ (1) 式中：σca为考虑结构局部屈曲时钢材的容许应力；σcag为不考虑结构局部屈曲时钢材的容许应力，与结构长细比有关（考虑了整体稳定）；σcal为有加劲肋且考虑局部屈曲的钢材容许应力；σcao为不考虑结构局部屈曲时钢材的容许应力。
2. 节段模型试验
2.1 模型设计与制作
在实桥凸形拱肋截面中约1/4跨径处截面的上下箱截面高度较高，该处截面发生局部屈曲的可能性较大，因此，以该截面作为试验对象。在综合考虑结构的外形尺寸、制作安装、加载方式及试验场地等因素，最终确定了模型与实桥的长度相似比为1∶4。拱肋节段模型采用与实桥拱肋相同的钢板Q345。
模型总体布置见图 3，加工后的具体形状见图 4。本节段模型模拟的是拱肋截面轴向受压时的受力特性，试验中将两加载端部放置于灌注机油的底座钢板上，以便模型在纵向上可以自由移动。为防止节段模型的两端部在加载过程中发生局部损坏，节段模型的两端采用钢-混凝土组合结构的形式进行局部加强处理。在节段模型端部焊接2块钢板，距离0.5 m，用工字钢和钢管进行钢板之间的连接，并支模浇注混凝土，加强段和节段模型用加劲腋板连接，使工字钢和混凝土共同承受外界施加的荷载，并将荷载均匀传至模型。此外，为防止加载端屈曲，将靠近加载端部的横隔板间距减小一半。
2.2 测点布置
试验是为了确定轴压荷载作用下凸形拱箱发生局部失稳或材料达到屈服极限时的荷载，故对加载过程中各板平面内的应变和出平面的位移（垂直板件中面的位移）测量是试验的主要测试内容。
为能监测构件局部屈曲的部位以及顶板、中板、底板和腹板的应变，测点均沿构件的长度方向成排布置。在顶板、中板、底板均设3条纵向应变监测线及1条横向应变监测线；在左右两侧的上腹板、下腹板均设置2条竖向和2条横向的应变监测线。同时，为了能测得加劲板在加载时的应力状态，在相应位置也布置了应变片。整个构件共布置应变片337片。为能够量测节段模型的局部变形及整体滑移等，在构件的不同位置布置了相应的位移计。在顶板、底板上各布置3个竖向位移计和1个纵向位移计，在一侧的上下腹板各布置3个横向位移计和1个纵向位移计，共布置16个位移计。
2.3 加载方式
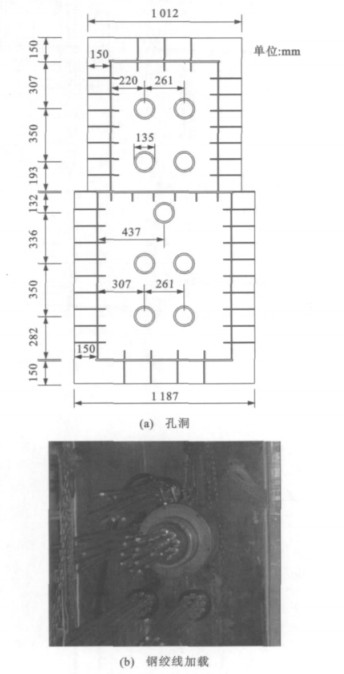
根据《钢结构设计规范》（GB50017—2003）[7]中考虑构件长细比的构件承载力计算方法，可以得到该截面可承受的屈服荷载为23024 kN，故初定最终试验荷载为23500 kN。若按常规的试验加载方式，需要强劲的反力架和复杂的荷载分配装置，为避免上述问题，采用预应力自反力加载方式，具体的做法是在节段模型的两端焊接加载端板，并将节段模型的两端做局部加强处理，在加载端板上开9个孔洞，以供预应力钢绞线的贯穿。为了避免加载时产生过大的偏心弯矩，孔洞的位置严格按模型形心的位置来定，使各孔洞预应力钢绞线的合力与模型截面的形心相重合。加载端板孔洞及钢绞线加载见图 5。待钢绞线穿过孔洞后，在模型一端安装锚头，另一端安装千斤顶逐根张拉钢绞线，对试件施加荷载。模型加载采用的预应力钢绞线为7Φ5 mm，面积为138 mm 2，标准强度为1860 MPa，每根钢绞线张拉的最大值为其标准强度的0.75倍。加载时采用117束7Φ5 mm的钢绞线，每孔13束，加载工况见表 1。
表 1 加载工况Table 1. Loadin gcases工况 张拉次数 步长/kN 每孔轴力/kN 截面总轴力/kN 截面平均应力/MPa 1 3 290.3 871 7840 124.3 2 3 290.3 1742 15680 248.7 3 2 290.0 2322 20898 346.2 4 1 289.0 2611 23500 372.7 3. 有限元模型
本文采用通用有限元软件MSC.Marc建立节段缩尺有限元模型，对结构进行单元离散是有限元分析的第一步。单元划分采用手动划分的形式，选用含横剪变形的4节点四边形双曲Shell75单元，保证在每一几何曲线上划分成的单元数为偶数，带横隔板截面的有限元单元划分见图 6（a）。在模型长度方向，设置单元长度均为12.5 cm，见图 6（b）。由于拱肋节段缩尺模型均由单一钢板焊接而成，故除两端加载端板采用Solid7模拟外，均采用Shell75单元模拟。整个有限元模型共划分成12484个单元，有限元网格见图 6（c）。根据缩尺模型试验的实际边界情况，有限元模型中限制加载端底面单元的竖向及横向两个方向的平动，并在加载端板预应力孔洞的中心位置施加压力。
采用理想弹塑性模型模拟Q345钢材的应力-应变关系，钢材的屈服应力等特征值根据材性试验的实测值确定。钢材的屈服条件满足Von Mises准则。
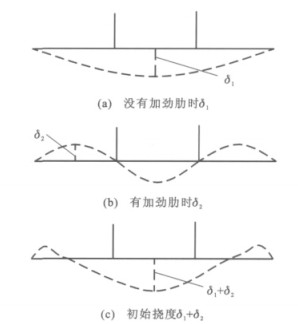
初始挠度根据《道路桥示方书》中的相关结果进行设定，假定在没有加劲肋时钢板板宽范围内的变形形状δ1呈正弦半波；有加劲肋时，相邻两加劲肋间的变形形状δ2也为正弦半波。δ1与δ2叠加的结果即为各钢板的初始挠度，见图 7。δ1、δ2分别为
$$ \left\{\begin{array}{l}\frac{\delta_{1}}{B}=2\left(7.5 \times 10^{-6} \frac{B}{t}\right) \\ \frac{\delta_{2}}{b}=2\left(5.0 \times 10^{-5} \frac{b}{t}\right)\end{array}\right. $$ (2) 式中：B为钢板宽度；t为钢板厚度；b为相邻两加劲肋间距。
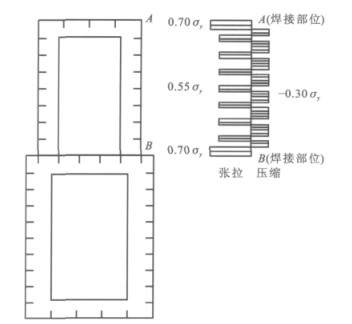
残余应力对构件来说是存在于截面内自相平衡的初始应力，钢材焊接时产生的残余应力是钢结构的最主要的一种残余应力，因此，残余应力的大小及分布与加工方法、加工过程密切相关。本文根据《道路桥示方书》及文献[8-12]模拟残余应力的分布，以一侧的上腹板为例，其残余应力的分布见图 8，图中σy为钢材的屈服应力。
4. 计算结果分析
4.1 测点应力与截面平均应力
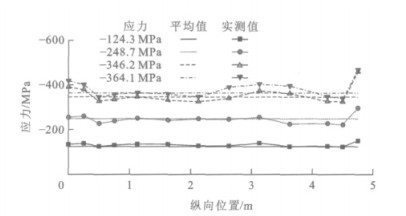
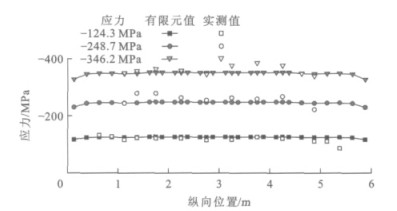
定义截面平均应力为施加的轴压荷载与截面积之比。测点应力为试验实测的各点应变，并根据自身所处的应力状态分别按照单向应力状态或平面应力状态计算所得的应力。以中板为例，加载试验截面平均应力为-124.3、-248.7、-346.2、-364.1 MPa时，各测点应力沿纵向的分布见图 9。可以看出，在加载过程中，除模型两端部外，各荷载等级下测点应力与截面平均应力较接近，这说明拱肋节段缩尺模型在加载过程中未产生偏心，两加劲端板能够有效传递荷载，模型处于轴压受力状态。当截面平均应力分别为-124.3、-248.7、-346.2 MPa时，实测应力和有限元模型的计算值沿纵向的分布见图 10，从图中可以看出二者较为接近，因此，该有限元模型具有较高的精度，能够较好地模拟缩尺模型的荷载试验过程。
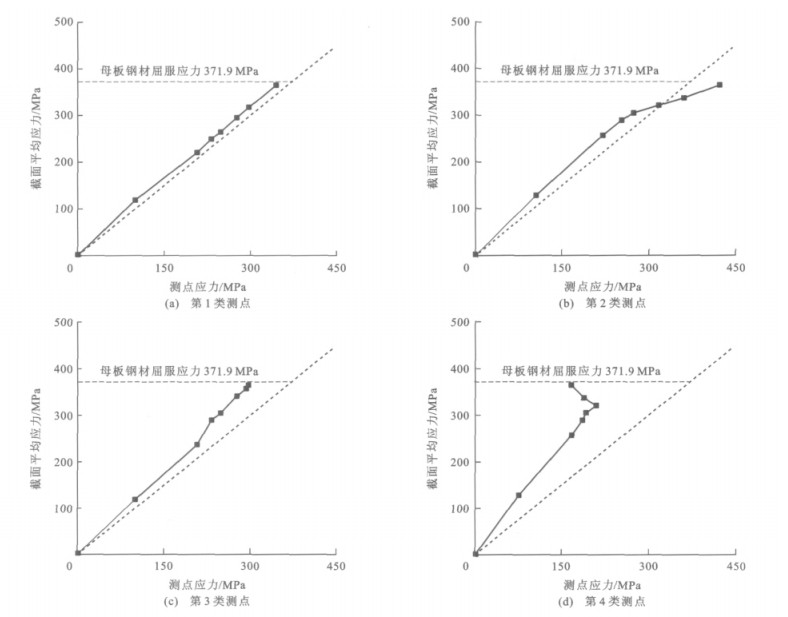
为了能够准确统计各测点达到屈服极限时的截面平均应力，比较各测点应力值与截面平均应力值可以看出，由于制作误差引起的结构初始变形、焊接应力等因素的影响，各测点应力与截面平均应力之间存在着一定的差异，可以将各测点应力与截面平均应力的变化过程大致分成4类，见图 11。其中，图 11中45°虚线表示测点应力与截面平均应力按1∶1线性增加。
图 11 测点应力与截面平均应力之间的关系Figure 11. Relationships between measured stresses and section average stresses第1类测点见图 11（a），在整个加载过程中始终处于轴心受压状态，其纵向应变变化特点是：在整个加载过程中，应变随截面平均应力成比例增加。这些测点直至整个节段模型加载至最后一个工况，板件未屈服。
第2类测点见图 11（b），外荷载较小时板件处于轴心受压状态，随截面平均应力的增加应变按比例增加；当截面平均应力增加到一定水平时，板件向箱内侧凹弯，板件进入压弯受力状态，轴向压应变与弯曲压应变叠加后，测点应变迅速增加，很快达到流限。
第3类测点见图 11（c），外荷载较小时板件处于轴心受压状态，随截面平均应力的增加应变按比例增加；当截面平均应力增加到一定水平时，板件向箱外侧凸出，板件进入压弯受力状态，轴向压应变与弯曲拉应变叠加后，测点应变增长变缓。
第4类测点见图 11（d），在外荷载很小时板件就处于受压弯状态，且板件是向箱外侧凸弯，这些测点处的轴向压应变与弯曲拉应变叠加，在整个加载过程中，应变都较同一应变测量线上其他测点处的应变要小，直至荷载加到最大值时这些测点上板件外表面处的应变均较小。
4.2 截面承载力
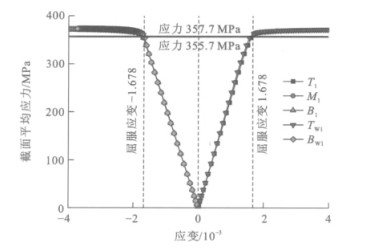
根据上述对各类应变变化规律的分析，统计所有测点应力达到流限时对应的截面平均应力值，对于第3、4类测点，流限值根据测点处压弯一侧的应变值确定。通过统计可得实测截面发生局部屈曲时的平均应力为343.2~357.8 MPa。
按照《道路桥示方书》中标准箱梁的方法来计算该凸形截面的抗压强度时，根据凸形截面的板件大小和加劲情况可不用考虑局部屈曲的影响，使得该凸形截面可承受的截面平均应力为365.1 MPa。
定义考虑局部屈曲的截面强度折减系数β为
$$ \beta=\sigma_{\text {cal }} / \sigma_{\text {cao }} $$ (3) 则通过模型试验可以得到该凸形截面强度折减系数β为0.94~0.98。
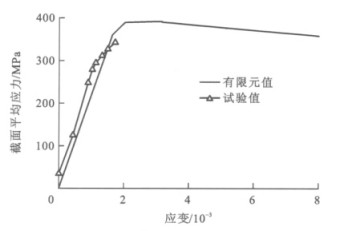
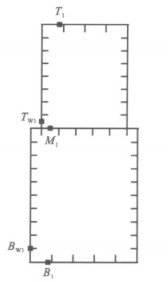
在有限元计算中，取长度方向3.25 m处位于两横隔板间的截面为研究对象，该截面处各测点的应力-应变曲线和有限元分析得到的应力-应变曲线的变化趋势一致且数值接近，以中板为例，二者的比较见图 12。选取该截面每块母板中应变增长最快、最有可能发生局部屈曲的点（图 13中T1、M1、B1、TW1、BW1），这些点的截面平均应力-应变曲线见图 14。可以看出，当荷载施加至22430 kN，即截面平均应力为355.7 MPa时，中板、底板的应变达到屈服应变；当荷载施加至22556 kN，即截面平均应力为357.7 MPa时，顶板、上下腹板的应变达到屈服应变，因此，通过有限元计算得到的该凸形截面平均应力在355.7~357.7 MPa之间，则通过有限元计算得到该凸形截面强度折减系数为0.97~0.98，与模型试验所得到的0.94~0.98相类似。
图 14 应力最大点的截面平均应力-应变曲线Figure 14. Section average stress-strain curves with maximum stress points模型试验和有限元分析结果均表明，局部屈曲对设计的凸形拱肋截面轴向容许抗压强度的影响很小，该凸形截面强度折减系数为0.94~0.98。
4.3 截面变形形态
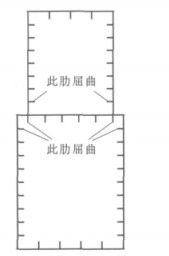
加劲肋结构是为了保证主要受力构件不提前发生局部屈曲而设置的，在整个试验过程中，横向加劲肋未发生屈曲变形，对于纵向加劲肋，除靠近中板的几道纵向加劲肋发生明显的屈曲变形外，其余处在弹性阶段，说明该凸形拱肋截面的加劲肋结构总体设计合理，能有效防止主要受力构件的局部屈曲。
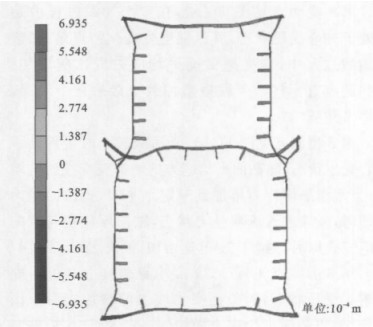
图 15、16中，发生局部屈曲的纵向加劲肋的位置主要在截面刚度发生较大变化的中板附近。图 17为有限元计算得到的截面变形形态，可以看出，在轴压荷载下，顶板、中板、底板与腹板交接的各角点的变形比各板中间部分的变形大，且中板处角点变形比顶板、底板的角点变形大，因此，对于凸形截面，应注意各角点附近的纵向加劲肋的设计，特别是中板处角点附近的纵向加劲肋。
4.4 屈曲形态
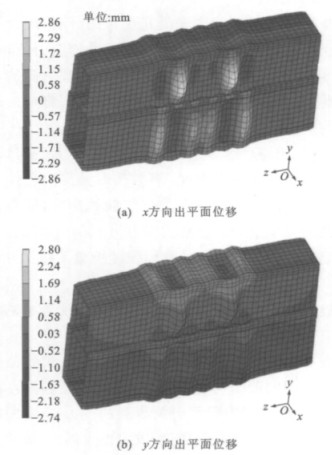
由于节段模型布置的预应力有限，且从安全的角度出发，所施加的试验荷载不能使试验模型发生明显的屈曲变形，因此，通过有限元计算得到极限荷载作用下试验模型的屈曲形态。在极限荷载下试验模型的整体变形见图 18，此时，横隔板应力很小，其余各板件的应变只略大于钢材屈服应变；左右按实桥尺寸缩放后横隔板加密一倍的1.5 m段未出现较大的变形，中间与实桥成比例的3 m段出现了凹凸的波节，说明由于中间3 m段板件发生了局部屈曲，由于各板出平面位移过大而导致其无法继续承载。
5. 结语
（1）在各荷载等级下试验得到测点应力与截面平均应力较接近，表明拱肋节段模型处于轴压的受力状态，根据测点应力与截面平均应力之间的关系可将凸形截面分成4类测点。有限元所得应力与实测应力趋势相同，数值相近，说明有限元模型能较准确地模拟试验模型。
（2）局部屈曲对该凸形拱肋截面轴向抗压强度的影响很小，通过模型试验和有限元分析得到该凸形钢箱拱肋截面的强度折减系数为0.94~0.98。
（3）凸形拱肋截面的纵向加劲肋和横隔板结构能有效地防止主要受力构件的局部屈曲，但应注意各角点附近的纵向加劲肋的设计和施工，特别是中板处角点附近的纵向加劲肋。
（4）在极限荷载作用下节段出现了凹凸的波节，由于各主要板出平面位移过大而导致无法继续承载。
-
图 11 测点应力与截面平均应力之间的关系
Figure 11. Relationships between measured stresses and section average stresses
图 14 应力最大点的截面平均应力-应变曲线
Figure 14. Section average stress-strain curves with maximum stress points
表 1 加载工况
Table 1. Loadin gcases
工况 张拉次数 步长/kN 每孔轴力/kN 截面总轴力/kN 截面平均应力/MPa 1 3 290.3 871 7840 124.3 2 3 290.3 1742 15680 248.7 3 2 290.0 2322 20898 346.2 4 1 289.0 2611 23500 372.7 
下载: 导出CSV
-
[1] CHEN Bao-chun, CHEN Kang-ming, NAKAMURA S, et al. A survey of steel arch bridges in China[J]. Journal ofCivil Engineering and Architecture, 2011, 5(9): 799-808. [2] 足立正和, 崎元達郎, 村上秀樹, 等. 鋼製八角形断面柱脚の局部座屈考慮した応力—ひずみ型復元力モデル[J]. 構造工学論文集, 2001, 47A(1): 65-76.ADACHI M, SAKIMOTO T, MURAKAMI H, et al. Hysteretic stress-strain models for octagonal cross-section steel piers in consideration of local buckling[J]. Journal of Structural Engineering, 2001, 47A(1): 65-76. [3] 龚建峰, 马骉, 吴伟胜. 宁波五路四桥大跨径桥梁设计综述[J]. 城市道桥与防洪, 2008(10): 66-71. doi: 10.3969/j.issn.1009-7716.2008.10.018GONG Jian-feng, MA Biao, WU Wei-sheng. General description on large-span bridge design of five roads and four bridges in Ningbo[J]. Urban Roads Bridges and Flood Control, 2008(10): 66-71. (inChinese doi: 10.3969/j.issn.1009-7716.2008.10.018 [4] 全军. 宁波明州大桥主桥设计与施工[J]. 世界桥梁, 2010, 38(2): 29-32. https://www.cnki.com.cn/Article/CJFDTOTAL-GWQL201002008.htmQUAN Jun. Design and construction of main bridge of Ming-zhou Bridge in Ningbo[J]. World Bridges, 2010, 38(2): 29-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWQL201002008.htm [5] 吴忠. 大跨度中承式双肢钢箱系杆拱桥施工工艺研究———宁波东外环甬江大桥施工方案比选[J]. 建筑施工, 2007, 29(4): 281-283. doi: 10.3969/j.issn.1004-1001.2007.04.022WU Zhong. Study on construction technology for long-span and mid-supported double steel-box tie-bar arch bridge-comparison and selection of construction proposal for Yongjiang Bridge in East Outer Ring Road of Ningbo[J]. Building Construction, 2007, 29(4): 281-283. (in Chinese) doi: 10.3969/j.issn.1004-1001.2007.04.022 [6] 周超舟, 姚森. 大跨度中承式双肢钢箱系杆提篮拱桥施工方案研究[J]. 桥梁建设, 2008(6): 53-56, 83. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS200806014.htmZHOU Chao-zhou, YAO Sen. Research of construction schemes for a long span half-through basket handle tied arch bridge with double-leg steel box section[J]. Bridge Construction, 2008(6): 53-56, 83. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS200806014.htm [7] GB 50017—2003, 钢结构设计规范[S].GB 50017—2003, code for design of steel structures[S]. (in Chinese) [8] 﨑元達郎, 渡辺浩, 中島黄太. 局部座屈を考慮した鋼箱形断面部材の復元力モ デ ル[J]. 土木学会論文集, 2000(647): 343-355. https://cdmd.cnki.com.cn/Article/CDMD-10724-1015960690.htmSAKIMOTO T, WATANABE H, NAKASHIMA K. Hysteretic models of steel box members with local buckling damage[J]. Proceedings of Japan Society of Civil Engineers, 2000(647): 343-355. https://cdmd.cnki.com.cn/Article/CDMD-10724-1015960690.htm [9] 渡辺浩, 﨑元達郎. コンクリートを充填した角形鋼管柱の局部座屈を考慮し た地震応答解析[J]. 土木学会論文集, 2000(647): 357-368.WATANABE H, SAKIMOTO T. Seismic response analysis of concrete-filled steel box piers considered on local buckling[J]. Proceedings of Japan Society of Civil Engineers, 2000(647): 357-368. [10] HASEGAWA A, ABO H, MAUROOF M, et al. Optimum cross sectional shapes of steel compression members with local buckling[J]. Proceedings of Japan Society of Civil Engineers, 1985, 2(1): 121-129. [11] HASEGAWA A, ABO H, MAUROOF M, et al. A simplified analysis and optimality on the steel column behavior with local buckling[J]. Proceedings of Japan Society of Civil Engineers, 1986, 3(2): 195-204. [12] 崎元達郎, 鶴田栄一, 木下照章, 等. 局部座屈とねじりを考慮した鋼箱形断面を有する骨組の終局挙動解析法[J]. 構造工学論文集, 2002, 48A(1): 87-97.SAKIMOTO T, TSURUTA E, KINOSHITA T, et al. A numerical method of analysis of steel frames considering local buckling and torsion[J]. Journal of Structural Engineering, 2002, 48A(1): 87-97. -
下载:
点击查看大图
计量
- 文章访问数: 1128
- HTML全文浏览量: 171
- PDF下载量: 916
- 被引次数: 0
