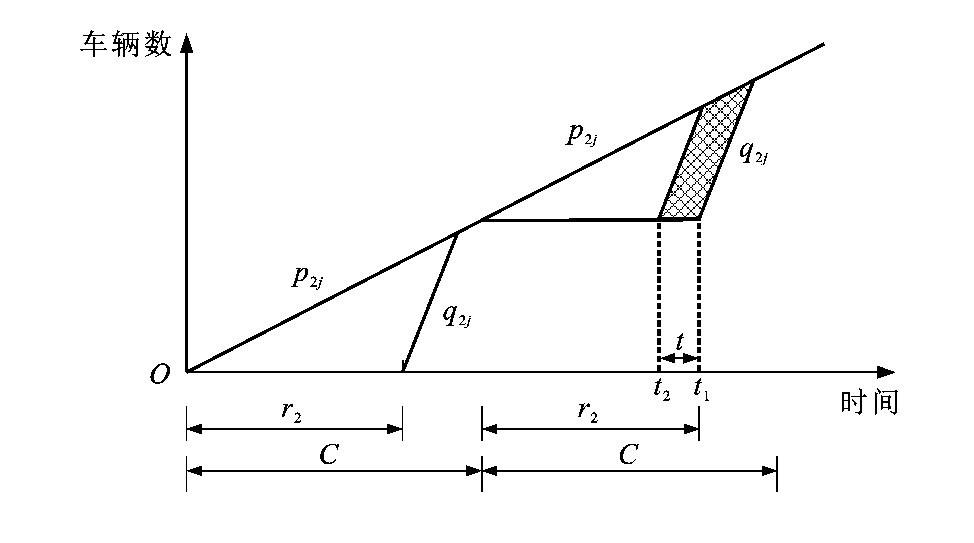
-
摘要: 以车辆延误和交叉口饱和度为约束条件, 针对绿灯提前和绿灯延长2种优先策略, 建立了求解有轨电车信号优先时长阈值的优化模型, 考虑了有轨电车车身长度的影响, 通过案例对模型进行验证。分析结果表明: 绿灯提前策略下优先时长的阈值为0~13s, 绿灯延长策略下优先时长的阈值为5~11s;以出行者作为研究单元时, 不同的非优先相位的公交车辆数对应不同的整体效益曲线, 而以车辆作为研究单元时, 不同的非优先相位的公交车辆数只对应一条整体效益曲线; 非优先相位的公交车辆数的临界值为16veh, 非优先相位的车辆到达率的临界值为0.115pcu·s-1, 红灯时长的临界值为101s, 这些参数超过临界值后, 不再适合给有轨电车设置信号优先。本文提出的有轨电车信号优先时长阈值的优化模型为给予有轨电车合理范围内的信号优先提供了依据。Abstract: Vehicle delay and intersection saturation were taken as constraint conditions, early green and extended green priority strategies were used, and the model of solving signal priority time threshold of tram was built.The influence of tram length was considered, and the model was verified through real case.Analysis result shows that the priority time thresholds under early green strategy are 0-13 s, and the priority time thresholds under extended green strategy are 5-11 s.When travelers are regarded as research units, different bus numbers under non-priority phase correspond to different overall benefit curves.When vehicles are regarded as research units, different bus numbers under non-priority phase correspond to only one overall benefit curve.The critical value of bus number under non-priority phase is 16 veh, the critical value of vehicle arrival rate under non-priority phase is 0.115pcu·s-1, and critical value of red time is 101 s.When they exceed critical values, it is not suitable to set signal priority for tram.The optimization model of signal priority time threshold of tram in this paper provides basis for giving signal priority of tram within reasonable range.
-
Key words:
- rail transit /
- tram /
- signal priority /
- priority strategy /
- priority time threshold /
- traveler delay
-
图 1 绿灯提前策略下优先相位减少的延误
Figure 1. Decreased delay of priority phase under early green strategy
图 2 绿灯提前策略下非优先相位增加的延误
Figure 2. Increased delay of non-priority phase under early green strategy
图 3 绿灯延长策略下优先相位减少的延误
Figure 3. Decreased delay of priority phase under extended green strategy
图 4 绿灯延长策略下非优先相位增加的延误
Figure 4. Increased delay of non-priority phase under extended green strategy
图 5 两种策略下非优先相位单个车辆的延误
Figure 5. Single vehicle delays of non-priority phase under two strategies
图 6 两种策略下非优先相位交叉口的饱和度
Figure 6. Intersection saturations of non-priority phase under two strategies
图 7 两种策略下非优先相位交叉口的整体效益
Figure 7. Intersection overall benefits of non-priority phase under two strategies
-
[1] 中国城市轨道交通协会. 城市轨道交通2014年度统计分析报告[R]. 北京: 中国城市轨道交通协会, 2015. China Association of Metros. Annual statistical analysis report of urban rail transit in 2014[R]. Beijing: China Association of Metros, 2015. (in Chinese). [2] 王舒祺. 现代有轨电车交叉路口优先控制管理方法研究综述[J]. 城市轨道交通研究, 2014, 17(6): 17-22. https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201406007.htmWANG Shu-qi. Study on signal priority control of modern tramcar at intersection[J]. Urban Mass Transit, 2014, 17(6): 17-22. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201406007.htm [3] SERMPIS D, PAPADAKOS P, FOUSEKIS K. Tram priority at signal-controlled junctions[J]. Transport, 2012, 165(2): 87-96. [4] GATENBY M, FEDZIN S. Traffic signal network operation within the Nottingham Express Transit system[J]. Traffic Engineering and Control, 2004, 45(2): 44-49. [5] SHALABY A, ABDULHAI B, LEE J. Assessment of streetcar transit priority options using microsimulation modelling[J]. Canadian Journal of Civil Engineering, 2003, 30(6): 1000-1009. doi: 10.1139/l03-010 [6] MATSUMOTO S, KUMAGAO Y, KAWASGIMA H. A study on the traffic signal strategy in city traffic consideration of streetcar[J]. Japan Society of Civil Engineers, 2004, 21: 677-685. [7] JEONG Y, KIM Y. Tram passive signal priority strategy based on the MAXBAND model[J]. KSCE Journal of Civil Engineering, 2014, 18(5): 1518-1527. doi: 10.1007/s12205-014-0159-1 [8] ZHOU Yang-fan, JIA Shun-ping, MAO Bao-hua, et al. An arterial signal coordination optimization model for trams based on modified AM-BAND[J]. Discrete Dynamics in Nature and Society, 2016, 2016: 1-10. [9] 张伟, 王军利, 王瑞斌. 快速公交信号优先控制研究[J]. 中国人民公安大学学报: 自然科学版, 2010, 16(4): 28-31. doi: 10.3969/j.issn.1007-1784.2010.04.007ZHANG Wei, WANG Jun-li, WANG Rui-bin. Study on signal priority control for bus rapid transit[J]. Journal of Chinese People's Public Security University: Science and Technology, 2010, 16(4): 28-31. (in Chinese). doi: 10.3969/j.issn.1007-1784.2010.04.007 [10] WEI Li-ying, ZHANG Li-li, WANG Zhi-long. A cellular automata model on bus signal priority strategies considering resource constraints[J]. Practical Applications of Intelligent Systems, 2014, 279: 689-698. [11] 马万经, 吴明敏, 韩宝新, 等. 考虑可变速度调节的单点交叉口公交信号优先控制方法[J]. 中国公路学报, 2013, 26(2): 127-133. doi: 10.3969/j.issn.1001-7372.2013.02.018MA Wan-jing, WU Ming-min, HAN Bao-xin, et al. Bus signal priority control method for isolated intersection based on dynamic variable speed adjustment[J]. China Journal of Highway and Transport, 2013, 26(2): 127-133. (in Chinese). doi: 10.3969/j.issn.1001-7372.2013.02.018 [12] MIRCHANDANI P B, LI J Q, HICKMAN M. A macroscopic model for integrating bus signal priority with vehicle rescheduling[J]. Public Transport, 2010, 2(3): 159-172. doi: 10.1007/s12469-010-0028-3 [13] KIM S, PARK M, CHON K S. Bus signal priority strategies for multi-directional bus routes[J]. KSCE Journal of Civil Engineering, 2012, 16(5): 855-861. doi: 10.1007/s12205-012-1507-7 [14] KOEHLERL A, KRAUS W J. Simultaneous control of traffic lights and bus departure for priority operation[J]. Transportation Research Part C: Emerging Technologies, 2010, 18(3): 288-298. doi: 10.1016/j.trc.2009.01.007 [15] BAGHERIAN M, MESBAH M, FERREIRA L. Using delay functions to evaluate transit priority at signals[J]. Public Transport, 2015, 7(1): 61-75. doi: 10.1007/s12469-014-0090-3 [16] 杨远舟, 毛保华, 张建鹏, 等. 基于元胞自动机模型的快速公交信号优先仿真研究[J]. 中国公路学报, 2010, 23(5): 90-95, 106. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201005013.htmYANG Yuan-zhou, MAO Bao-hua, ZHANG Jian-peng, et al. Research on signal priority simulation for bus rapid transit using cellular automaton model[J]. China Journal of Highway and Transport, 2010, 23(5): 90-95, 106. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201005013.htm [17] AHMED F, HAWAS Y E. An integrated real-time traffic signal system for transit signal priority, incident detection and congestion management[J]. Transportation Research Part C: Emerging Technologies, 2015, 60: 52-76. doi: 10.1016/j.trc.2015.08.004 [18] ZHOU Guang-wei, GAN A, SHEN L D. Optimization of adaptive transit signal priority using parallel genetic algorithm[J]. Tsinghua Science and Technology, 2007, 12(2): 131-140. doi: 10.1016/S1007-0214(07)70020-2 [19] HU Jia, PARK B B, LEE Y J. Coordinated transit signal priority supporting transit progression under connected vehicle technology[J]. Transportation Research Part C: Emerging Technologies, 2015, 55: 393-408. doi: 10.1016/j.trc.2014.12.005 [20] WAHLSTEDT J. Impacts of bus priority in coordinated traffic signals[J]. Procedia-Social and Behavioral Sciences, 2011, 16: 578-587. doi: 10.1016/j.sbspro.2011.04.478 [21] LIU Hong-chao, ZHANG Jie, CHENG Ding-xin. Analytical approach to evaluating transit signal priority[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(2): 48-57. [22] 朱晓宁, 隆冰. 多路公交优先交叉口配时优化的双层规划模型[J]. 交通运输工程学报, 2014, 14(1): 103-111. http://transport.chd.edu.cn/article/id/201401014ZHU Xiao-ning, LONG Bing. Bi-level programming model of timing optimization for multiple bus priority intersection[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 103-111. (in Chinese). http://transport.chd.edu.cn/article/id/201401014 [23] 孙煦, 陆化普. 公交优先下交叉口配时优化的双层模型与遗传算法[J]. 北京工业大学学报, 2012, 38(6): 859-864. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201206011.htmSUN Xu, LU Hua-pu. Bi-level optimization model of intersection timing about bus priority condition based on genetic algorithm[J]. Journal of Beijing University of Technology, 2012, 38(6): 859-864. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201206011.htm [24] 杨晓光, 林瑜, 杭明升. 信号控制交叉口公共汽车优先信号确定方法研究[J]. 中国公路学报, 2001, 14(增): 101-104, 108. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL2001S1025.htmYANG Xiao-guang, LIN Yu, HANG Ming-sheng. Study of solution for transit priority signal[J]. China Journal of Highway and Transport, 2001, 14(S): 101-104, 108. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL2001S1025.htm -
下载:
点击查看大图
图(11) / 表(1)
计量
- 文章访问数: 2148
- HTML全文浏览量: 168
- PDF下载量: 1732
- 被引次数: 0
