目前, 国内对集装箱运价的研究, 多以定性分析为主^[1-2], 然而, 运价终究是由市场中供、求的互相作用来决定的^[3-4], 不考虑供求关系的模型是不合理的。本文试图对集装箱运价建立一种基于供求关系分析的预测模型, 用数学推导的方法得出箱运市场的经济学模型, 并同时得出一些重要的结论。

1.   航运生产函数的定义

一艘集装箱船的运输生产能力取决于两个要素: 箱位数和航速, 本节以此为出发点, 推导出一些函数, 给定这些函数, 航运业可以使用不同的燃油消耗和箱位数组合来达到某一产量水平。

1.1   基本生产关系

航运业的产品是运输, 可以箱海里来衡量集装箱运输业的产品, 生产的基本单位是船舶或船队。因此, 对i艘船舶来说, 若生产函数以每天箱海里为指标, 自变量为船舶载箱能力X₁和营运航速X₂, 则

$Q{}_i=24X{}_{1i}X{}_{2i}(1)$

式中: Q_i每天箱海里(第i艘船); X₁为船舶箱位数(TEU); X₂为营运航速(节)。

从短期看, 航线运力的制约为船队总载箱能力X₁^*、船队最大设计航速X₂^*[5]。从长期看, 通过订造新船, X₁和X₂都可改变。

船舶营运航速可认为是每天每箱位投入燃油数量的函数, 其范围是上限为最大设计航速, 下限为主机低速运转的技术能力。在这个范围内, 燃油消耗和航速的关系可由下式近似表示

$X{}_{2i}=X{}_{2i}^{*}(X{}_{3i}/X{}_{3i}^{*}){}^{\alpha }(2)$

式中: α为船舶燃油效率系数(对低速柴油机船, α=1/3);X₃为每天每箱位耗油量; X₃^*为最大设计航速时燃油消耗数。

上式实际上是一种燃油效率函数, 说明船队全速营运时, 要增加运力只能靠增加船舶。

燃油投入量越接近最大设计航速燃油消耗额, 航速越高。取代X₂, 可以两个基本生产要X₁素和X₃重新定义生产函数

Q_i=24X_1iX_2i^* (X_3i/X_3i^*)^α (3)

简化得Q_i=A_iX_1iX ${}_{3i}^{\alpha }$ (4)

A_i=24X_2i^* (1/X_3i^*)^α (5)

式(4) 表示, 以每天箱海里为指标的运输生产函数是常数A、投入载箱能力X₁和每天每箱位耗油量X₃的α次方。换言之, 产量的增长和所投入的载箱能力成比例增长, 但增加燃油投入的效果递减。常数A可定义为“船舶效率系数”, 因为它定义了第i艘船舶把1 kg燃油转化为所运输的箱海里的技术能力。每艘船舶的A值取决于其基本设计参数, 虽然船壳锈蚀、机械磨损都可使其值发生变化, 因此, 可以认为

$A{}_i=f(t)(6)$

就整个船队而言, 如新造船舶由于主机效率提高等原因而使性能发生了变化, 都将使参数A_i值发生变化。从短期看, 若船队的能力、状况设为固定, 则每船A值为常数。

1.2   船队生产函数

从单船进而考虑整个船队, 船队运力供应函数为每船供应函数之和

${\displaystyle \sum _{i}Q}{}_i={\displaystyle \sum _i(}A{}_{i}X{}_{1i}X{}_{3i}^{\alpha })(7)$

即总箱海里供应为每船产量之和。总产量的改变可由投入营运的船舶数X₁、每天每箱位耗油量X₃的改变而得。

1.3   船队效率函数

为便于分析, 假设可以船舶效率系数A的降序来排列船队, 燃油投入保持不变, 逐渐排除效率最低的船, 船队以每天箱海里计的产量因此而变, 生产函数可重写为

$Q{}_i={\displaystyle \sum _i(}A{}_i^{*}X{}_{1i}X{}_{3i}^{\alpha })(8)$

式中: A^*为已排序效率系数。

减少营运船数将增加A^*的边际值和平均值, 整个船队的A^*平均值为

$\overline{A}{}^{*}=\frac{{\displaystyle \sum _{i}A}{}_{i}X{}_{1i}}{{\displaystyle \sum _{i}X}{}_{1i}}=A{}^0(9)$

一定船舶数的船队的平均A⁰可设定为营运中船舶箱位数的某种简单函数

$A{}^0=f(X{}_1^0)(10)$

式中: X ${}_1^0$为以A值升序排列的营运船队(箱位数)。

本函数代表了一定的船队将燃油转化为运输的能力, 因此, 可定义为“船队效率函数”。假设船舶大小一致, 生产函数可简化为(去掉下标i)

$Q=A{}^{0}X{}_1^{0}X{}_3^{\alpha }=f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha }(11)$

式中: X ${}_1^0$为营运中船舶总箱位数; X₃为每天每箱位平均燃油投入。

1.4   燃油生产率函数

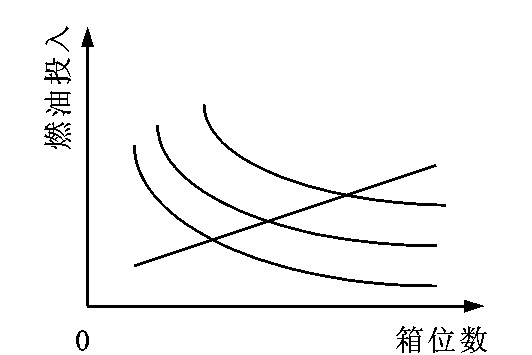
在一个相当大的范围内, 一定的船舶载箱能力的产量可通过改变使用的燃油数量而改变, 见图 1。

图  1  燃油生产率函数

Figure  1.  Fuel productivity function

下载: 全尺寸图片 幻灯片

图  2  箱位生产率函数

Figure  2.  TEU productivity function

下载: 全尺寸图片 幻灯片

通常认为航速低于最大设计速度为一种非正常情况, 但观察生产函数可知, 其实这种观点有局限性。造船工程师做这个假设的目的是优化流体动力学计算, 实际中, 船公司可选择各种燃油投入量和载箱能力组合以达到一定的产量水平, 而这种选择又受这两种要素相对价格的影响。

1.5   箱位生产率函数

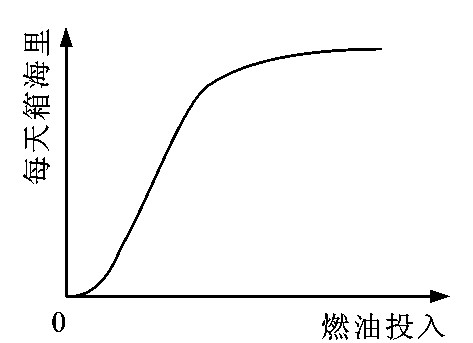
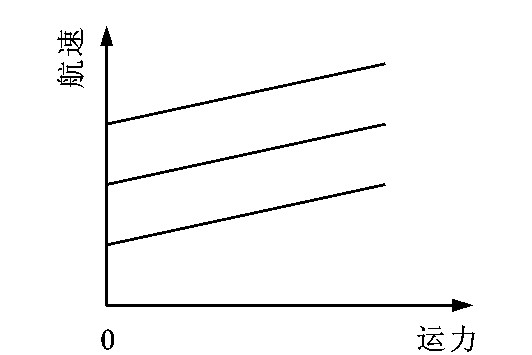
与燃油生产率函数类似, 保持每天每箱位燃油投入不变, 增加船舶艘数, 则箱位生产率函数代表所得的箱海里, 见图 2。

图  3  燃油的边际和平均产量

Figure  3.  Marginal and average productivity of fuel

下载: 全尺寸图片 幻灯片

1.6   燃油的边际及平均生产率

从式(2) 可以看出, 随着燃油投入量的增多, 产量的增加递减。边际产量(MP) 用于衡量因燃油消耗的微小增加而获得的产量的增加, 求式(11) 燃油消耗的偏导

${\rm M}{\rm P}{}_f=\frac{\text{d}Q}{\text{d}X{}_3}=\alpha f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha -1}(12)$

把上述关系标示于图 3。

正如所预期, 随着投入的增加, 燃油的边际产量递减。平均产量衡量的是总产量除以所使用的燃油总量, 其定义为

$A{\rm P}{}_f=\frac{Q}{X{}_1^{0}X{}_3}=\frac{f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha }}{X{}_1^{0}X{}_3}=f(X{}_1^0)X{}_3^{\alpha -1}(13)$

式中: AP_f为燃油的平均产量。

1.7   有效载箱能力(箱位) 的边际生产率

对船公司而言, 改变所投入的箱位数可以达到改变燃油消耗数量的同样效果。对于整个船队, 边际产量可以认为是把一艘闲置的船舶投入使用而增加的产量, 即效率最低的那艘船舶的平均产量, 从式(11) 得

${\rm M}{\rm P}{}_{slot}=\frac{\text{d}Q}{\text{d}X{}_1^0}=X{}_3^{\alpha }[X{}_1^{0}f{}^{´}(X{}_1^0)+f(X{}_1^0)](14)$

式中: MP_slot为箱位的边际产量; X₁⁰为已排序的投入使用的船队。

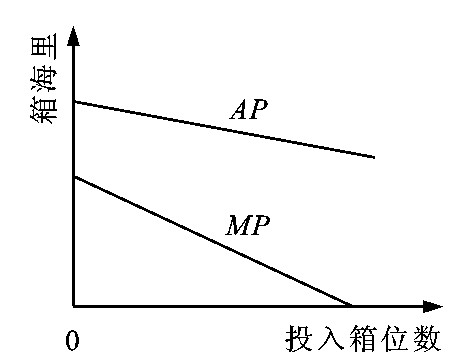
箱位边际产量函数见图 4, 箱位的平均产量可定义为

$A{\rm P}{}_{slot}=\frac{Q}{X{}_1^0}=\frac{f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha }}{X{}_1^0}=f(X{}_1^0)X{}_3^{\alpha }(15)$

图  4  运力(箱位) 的边际和平均产量

Figure  4.  Marginal and average productivity of TEU slot capacity

下载: 全尺寸图片 幻灯片

根据生产的两个基本要素——燃油和船舶定义了航运生产函数, 运输产量由所投入的燃油量决定。燃油的边际产量(即每天每箱位多投入1 kg燃油所额外获得的箱海里数) 随燃油投入量的增加而递减。类似地, 产量也可以通过改变投入运营的船舶箱位数而改变。为了考虑船舶效率不同的事实, 定义了“船队效率函数”。给定这些函数, 航运业可以使用不同的燃油消耗和箱位数组合来达到某一产量水平。要确定那一种组合利润最大(或亏损最小) 则要引入成本, 特别是“成本函数”。

2.   集装箱航运市场供方的短期单位总成本

本节从集装箱船舶运输生产的总成本为出发点, 推导出集装箱航运市场供方的短期单位总成本, 从而可以计算边际成本, 其中还得到了航运扩张路径等一些有用的结论。

2.1   集装箱航运市场供方成本函数

第i艘船舶进行运输生产的总成本(C_T) 可以定义为^[6]

$C{}_{{\rm T}i}=r{}_{1i}{\rm Z}{}_{i}X{}_{1i}+r{}_{3}X{}_{1i}X{}_{3i}{\rm Z}{}_i+{\rm K}{}_i{\rm Z}{}_{i}X{}_{1i}(16)$

式中: C_Ti为第i艘船的总成本; r₁为每天每额定载箱能力的平均营运成本; Z为航行天数; X₁为船舶载箱能力; r₃为每公斤燃油成本; X₃为每天每额定载箱能力耗油量; K为每天每额定载箱能力资本成本。

集装箱船舶成本由三部分组成: 营运成本, 为每天每箱位平均营运成本(r₁)、航行天数(Z)、船舶载箱能力(X₁) 的乘积; 燃油成本, 为每公斤燃油成本(r₃)、每天每箱位油耗(X₃)、航行天数、载箱能力的乘积; 资本成本, 为每天每额定载箱能力资本成本(K)、航行天数(Z) 和额定载箱能力的乘积。

式(16) 揭示了航速和时间之间的某种平衡: 航速降低, 燃油成本将降低, 但航行天数将增加, 而这会提升营运成本和资本成本。

以上是单船成本, 考虑整个船队就遇到一个问题: 各船由于船龄、吨位、船员配备、原始设计不同而使成本效率水平有很大不同。对式(16) 两边同除以X_1iZ_i, 就可以把成本降为每天每箱位成本的共同基础

$\begin{array}{l}C{}_i=r{}_{1i}+r{}_{3}X{}_{3i}+{\rm K}{}_i(17)\\ C{}_i=C{}_{{\rm T}i}/X{}_{1i}{\rm Z}{}_i\end{array}$

原则上, 可根据每天营运成本(r₁) 来对船舶进行排序。但这又引起一个基本问题, 这种排序如何与式(10) 中的燃油效率系数联系起来。这两种排序可能并不相关, 但为推导下去, 必须假设就整个船队它们平均相关。这样, 可定义每天营运成本的新函数, 自变量为已排序有效总载箱能力X ${}_1^0$

$r{}_1=g(X{}_1^0)(18)$

这是船队“成本效率函数”, 定义了不同产量水平上的单位成本, 则每天每载箱能力的成本函数为

$C=g(X{}_1^0)+r{}_{3}X{}_3+{\rm K}(19)$

式(19) 指出, 船队每天每箱位成本取决于投入使用的船舶吨位、所使用的燃油量、燃油价格和资本成本K。

2.2   等产量线和等成本线

为了达到某一固定产量, 船东可选择各种投入组合, 这些组合的全部由等产量线代表, 其定义如下

$Q{}^{*}=f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha }(20)$

式中: Q^*为每天以箱海里计的固定产量, 等产量线如图 5所示。

图  5  等产量线和扩张路径

Figure  5.  Isoquant and expansion path

下载: 全尺寸图片 幻灯片

分析的下一步是引入预算限制线, 它可以表示一定的资金所能购买的各种投入组合。预算线与Y轴的截距表示预算全部投入用于购买燃油所能达到的消耗水平, 与X轴的截距表示预算全部用于购买船舶所能达到的箱位数。实际中当然不可能出现这两种极端的情况, 预算线的定义为

$C{}^{*}=g(X{}_1^0)+r{}_{3}X{}_3(21)$

式中: C^*为每天每箱位固定成本; g (X₁⁰) 为已排序的投入使用的船队平均每箱位营运成本。

一定量的预算所能获得的最大产出是预算线和等产量线的切点, 此点所对应的投入组合为最佳组合。换言之, 理性的船公司将选择某种箱位数和燃油消耗的组合, 使产量最大, 成本最低。

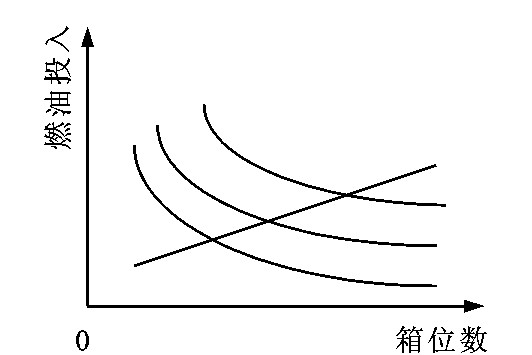
2.3   扩张路径

对一定的要素价格r₁和r₃, 在整个产量范围内把等产量线和等成本线之间的切点连成线, 就形成航运能力扩张路径。如果箱位和燃油的相对价格(r₁/r₃) 发生变化, 则等产量线和等成本线的切点发生变化, 因此扩张路径也将变化。例如, 1973年和1979年两次油价上涨的结果是最佳要素投入组合移向较多的吨位数、较慢的航速。用数学语言, 扩张路径可定义为一簇点的连线, 其上要素价格r₁和r₃的比例等于它们相应的边际产量的比例, 因此

$\frac{r{}_1}{r{}_3}=\frac{{\rm M}{\rm P}{}_{slot}}{{\rm M}{\rm P}{}_f}(22)$

代入式(12)、(14), 得

$\frac{r{}_1}{r{}_3}=\frac{X{}_3^{\alpha }[X{}_1^{0}f{}^{´}(X{}_1^0)+f(X{}_1^0)]}{\alpha f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha -1}}(23)$

简化得扩张路径

$\begin{array}{l}r{}_{1}X{}_1^0{\rm H}-r{}_{3}X{}_{3}G=0(24)\\ {\rm H}=\alpha f(X{}_1^0)\\ G=X{}_1^{0}f{}^{´}(X{}_1^0)+f(X{}_1^0)\end{array}$

式(24) 指出, 随着需求水平的变化, 船队的产量也扩大或收缩, 箱位数(X₁⁰) 和燃油量(X₃) 的平衡将取决于两个因素: 相对价格和船队效率。关于价格, 如果燃油价格(r₃) 相对箱位的价格(r₁) 发生改变, 则使用的燃油量相对数量将发生改变。船队效率情形略微复杂。式(24) 中的相对成本元素的权重分别为G和H, 其取值依赖于船队效率

图  6  扩张路径

Figure  6.  Fleet expansion path

下载: 全尺寸图片 幻灯片

函数和“燃油效率函数”见式(2), G值含有船队效率函数的一阶导数, 这意味着如果船队效率函数是非线性的, 则G值将随不同的产量水平而不同。扩张路径如图 6所示。

从上图得出海运供应函数的二个重要性质: ①当更多船舶投入营运, 航速有相对较小的增长, 这表示油价较高时期, 如果大多数闲置船舶都已投入使用, 船队才会加速; ②燃油价格对箱位价格比的改变对最佳航速有重大影响。如果在实际中这个关系确实存在, 随着实际燃油价格的改变, 航运业会运营在不同的“扩张路径”上。

2.4   短期单位成本函数

前面所得到的一系列方程一起就可定义船队的单位成本函数。生产函数式(8) 定义了一定产量所需要的燃油和箱位数, 扩张路径式(24) 定义在一组给定价格下最经济的要素投入组合; 总成本函数式(19) 使总成本得以计算。下列三式分别是总产量、总成本和扩张线路

$\begin{array}{l}Q=f(X{}_1^0)X{}_1^{0}X{}_3^{\alpha }\\ C=g(X{}_1^0)+r{}_{3}X{}_3+{\rm K}\\ r{}_{1}X{}_1^0{\rm H}-r{}_{3}X{}_{3}G=0\end{array}$

要求使函数f和g的形式具体化, 解方程组得作为Q函数的C, 求成本函数对产量的一阶导数得边际成本。根据经济理论, 在完全竞争市场中价格等于边际成本时利润最大, 这可作为航运供应函数。

3.   价格机制的模拟

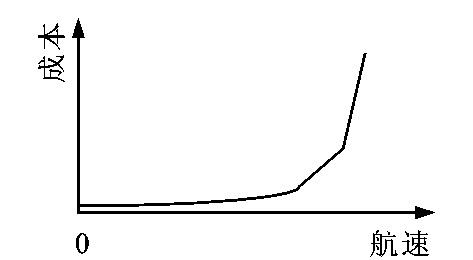
3.1   航速和边际成本的关系

对函数f和g引入简单的线性函数, 就可对成本函数产生一个数值模拟模型, 结果见图 7、8, 计算方法为: ①对一组给定价格, 利用扩张路径, 确定一定产量的要素投入组合; ②把载箱能力和每箱位耗油量代入生产函数以确定产出水平; ③利用成本函数, 确定在每个产量水平上相应的总变动成本; ④计算在每个产量水平上相应的总成本的变化, 作为边际成本, 不考虑资本成本, 因为短期定价决策中不含此项。

图  7  平均成本函数

Figure  7.  Fleet average cost function

下载: 全尺寸图片 幻灯片

图  8  产量的边际成本

Figure  8.  Marginal cost of output

下载: 全尺寸图片 幻灯片

3.2   边际成本和供应函数

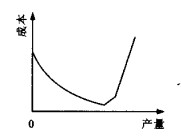
当产量增长时, 由于能力得到充分利用, 平均成本下降, 至某点达到最低, 之后边际成本开始迅速上升, 如图 9所示。

在建立航运模型时, 边际成本特别重要, 因为它定义了航运产出的可能供应函数。或者说, 它定义了船东提供额外运输所要求的价格。在完全竞争市场中, 当边际成本等于价格时, 船东的利润最大(或亏损最小), 同时表明社会效益的消费者剩余达到最大^[7], 这使边际成本函数的形状特别重要。图 9显

图  9  航速和边际成本

Figure  9.  Speed and marginal cost

下载: 全尺寸图片 幻灯片

示, 在一个大范围内, 边际成本对需求相对较不敏感, 运价相对稳定。但当船队已完全利用, 边际成本以及船东要求的运价上升很快, 通俗地讲, 这意味着当需求低于供应时运价将相对稳定, 当需求水平接近现有供应能力时, 运价将很不稳定。