0.   引言

以A380、B777为代表的新一代大型飞机具有轮轴构型复杂、起飞荷载大等特点, 使得目前基于经验的机场沥青道面结构设计方法已经不能够满足大型飞机发展的需要^[1-2], 一些研究者和研究机构已致力于力学-经验法的道面结构设计方法, 以应对新一代大型飞机的运营对道面结构设计的挑战。在20世纪70年代, 比较有代表性的是美国沥青协会制定的全厚度道面设计方法^[3]和美国空军制定的弹性层状体系法^[4]; 20世纪90年代中期, 随着新一代大型飞机的出现, 美国联邦航空局(FAA)基于弹性层状体系理论建立了包含B777机型的道面结构设计方法, 并编制了相关的设计程序LEDFAA^[5]。飞机轮载作用下道面结构的力学响应量的准确获取是力学-经验法设计的关键一步^[6-8]。

Sukumaran等分析了B777飞机荷载作用下沥青道面的力学响应, 采用的模型尺寸(滑行向、道面宽度方向、厚度方向)为13.71 m×18.28 m×3.00 m, 靠近荷载作用中心的单元最小, 模型共使用了4 526个缩减单元和336个无限单元^[9]; Saad等认为三维模型要比二维模型在分析时更具有优势, 提出汽车荷载作用时模型的几何尺寸(水平向、水平向、路面深度方向)为2.5 m×2.5 m×3.0 m^[10]; Kuo等认为水平向的尺寸应该为荷载作用面直径的3倍, 垂直向为1倍, 所有边界采用无限单元^[11]。然而以上分析都存在一定的局限性, 如无限单元虽然可以减少有限单元带来的误差, 但是静态分析时会增加计算的成本, 另外并未就全起落荷载作用时进行考虑。

本文以ABAQUS通用有限元软件为平台, 建立3层道面结构有限元模型, 分析模型几何尺寸、边界条件、层间接触条件、单元类型、网格的划分等对力学响应的影响, 提出适应大型飞机荷载特点的机场沥青道面结构有限元参数, 并利用现场实测的力学响应数据验证了模型参数的合理性。

1.   道面结构有限元模型边界条件

1.1   几何尺寸

弹性层状体系中对计算区域的假设为: 土基在水平方向和向下的深度方向均为无限, 其上的道面结构各层厚度均为有限, 但水平方向仍为无限。

数值模拟中一般采用扩大模型几何尺寸达到消除边界对计算结果的影响。尺寸选择的合理性不仅直接决定了计算的精度, 同时会对计算机的内存和CPU提出更高的要求。综合分析国内外对弹性层状体系有限元的模拟^[12-13], 结合大型飞机起落架尺寸的特点和荷载影响范围, 考虑全起落架荷载作用时, 模型平面尺寸宜选取为30 m×30 m。

为了验证有限元模型所取的结构厚度对计算结果的影响, 采用30 m×30 m的平面尺寸, 平面正中心作用0.3 m×0.3 m的方形荷载, 荷载大小为0.7 MPa, 道面结构基本参数见表 1。

表  1  道面结构参数

Table  1.  Parameters of pavement structure

结构层	厚度/m	弹性模量/MPa	泊松比
面层	0.10	1 400	0.35
基层	1.16	500	0.35
土基	4.00、8.00、12.00、16.00	120	0.40

下载: 导出CSV 

| 显示表格

荷载区域网格大小为0.05 m×0.05 m, 不同厚度条件下计算得到的表面最大弯沉见图 1。当厚度为8 m时, 道面表面的弯沉与16 m厚度的差值为0.66×10^-2 mm, 仅为16 m时的1.61%, 因而采用8 m以上的厚度对道面的结构响应分析来说已经足够, 在本文的分析中, 选择道面结构总厚度为10 m。

图  1  表面最大弯沉曲线

Figure  1.  Surface maximum deflection curve

下载: 全尺寸图片 幻灯片

大型机场沥青跑道宽度可达到60 m, 大型飞机起落架的间距一般在10 m左右, 按照以上分析, 考虑全起落架荷载作用时, 模型几何尺寸(沿着飞机滑行方向、垂直飞机滑行方向、厚度方向)为30 m×30 m×10 m, 满足计算精度的网格划分在现有的PC机上运行就变得非常困难。

利用荷载和几何的对称特性, 半对称的荷载其尺寸可缩减到30 m×15 m×10 m(1/2模型), 全对称的荷载其尺寸可采用15 m×15 m×10 m的模型尺寸(1/4模型), 2种模型分别见图 2、3。

图  2  30m×15 m×10 m模型

Figure  2.  Model of 30 m×15 m×10 m

下载: 全尺寸图片 幻灯片

图  3  15m×15 m×10 m模型

Figure  3.  Model of 15 m×15 m×10 m

下载: 全尺寸图片 幻灯片

1.2   边界条件

按照以上几何尺寸建立有限元模型, 约束模型底部的所有自由度, 层间接触采用tie连接, 单元类型选择为C3D8R, 控制荷载区域网格大小为0.05 m×0.05 m, 单元总数为69 696个。分别对水平向全部约束、约束1个水平方向、水平方向全部不约束3种不同的边界条件进行分析, 计算结果见表 2。

表  2  边界条件对计算结果的影响

Table  2.  Influences of boundary conditions on calculation results

边界条件	整个CPU使用时间/s	Mises应力/MPa	表面弯沉/mm	土基顶面压应变/10-5
约束某一个水平向的位移	603.1	0.586 5	0.406 9	-7.371
约束所有水平位移	381.7	0.584 9	0.404 4	-6.804
水平方向自由	7 699.3	0.586 6	0.408 7	-7.378
极差百分比/%		0.29	1.10	7.80

下载: 导出CSV 

| 显示表格

水平方向的边界约束对表面弯沉和最大Mises应力几乎没有影响; 随着深度的增加, 由于应力的扩散, 使得水平向的约束条件对计算结果的影响较表面要明显, 但其极差百分比也在10%以内。从整个CPU的时间来看, 随着约束条件的增强, 所需要的时间逐渐减少, 因为边界条件增多后, 使得在有限元计算时判断收敛变得更加容易, 这样所计算的时间就大大减少, 对于水平向全自由的边界条件, 在进行收敛判断时要根据底部的约束条件来进行, 这样就导致了计算时间的增加。

综合不同约束条件对计算结果的影响和所占用的整个CPU时间, 整个道面的边界条件为x方向边界v和y方向侧边界u均为0, v、u分别为沿坐标x、y方向的位移, 假定x方向为垂直于飞机滑行方向, y方向为飞机滑行方向, 土基底面为固定端约束。

1.3   层间接触条件

弹性层状体系理论中在层次之间的接触面上采用2种假定: 层间接触完全连续, 即在接触面上, 应力和位移完全连续; 层间接触完全光滑, 其上剪应力为0。

ABAQUS有限元软件中连接2个面并定义相互之间关系的接触模式有很多, 其中道路工程中经常使用的主要有tie连接、rough连接、层间剖分。tie和rough通过对2个不同的面之间设置属性, 来实现2个面之间的接触属性, 设置tie连接后使得相互作用的主面与从面之间的节点具有相同的物理量, rough连接控制的是主面与从面在水平方向的约束, 对于法向的约束还要重新进行定义, 例如要等价于完全连续则需要在法向进行约束。层间剖分则相对简单, 直接通过剖分将几何部件分成2个部分, 彼此之间并没有主面与从面的产生, 分开的2个部分完全联系在一起, 界面上的变形完全连续。

在以上建立的有限元模型基础上, 按照层间接触完全连续的假设, 分别采用tie、rough、层间剖分3种接触约束模拟, 计算结果见表 3。

表  3  层间接触条件对计算结果的影响

Table  3.  Influences of interfacing conditions on calculation results

类型	整个CPU使用时间/s	Mises应力/MPa	表面弯沉/mm	土基顶面压应变/10-5
tie	576.5	0.586 3	0.403 8	-7.352
rough	8 217.8	0.607 2	0.417 4	-7.030
层间剖分	500.3	0.585 3	0.403 0	-7.345
极差百分比/%		3.6	3.4	4.4

下载: 导出CSV 

| 显示表格

从表 3可知: 3种不同的层间连续条件的模拟对计算结果的差值都在5%以内, 可以认为对计算结果的影响相对较小, 可以忽略不计。tie连接是将临近的2个面的节点或是单元绑定在一起, 彼此之间没有相对位移, 在计算时, 这些节点具有相同的特性。rough约束包括了切向的约束和法向的约束, 这样在层间接触计算判定时要经历切向和法向的两次判断来平衡线性方程组, 将导致整个CPU时间急剧增加, 特别是当单元数量较多时所花费的计算机时更加明显。在实现层间完全连续模拟条件下, 3种不同的接触条件都能实现, 但是rough要占用更多CPU时间。在模拟层状体系的结构时, 层间完全连续时层间的接触可以采用tie连接或是直接建立一个部件进行剖分。但对于复杂结构, 为了方便后处理, 宜使用tie连接将不同的部件之间联系起来。

2.   有限元单元

2.1   单元类型

ABAQUS软件中为用户提供了丰富的有限元单元, 按照节点位移插值的阶数, 可以分为线性单元、二次单元、修正的二次单元; 按照积分方式的不同, 可以分为完全积分单元、减缩积分单元、非协调模式单元等。

有限元法仅仅在单元节点处计算位移、转动等自由度结果, 在单元内任何其他点处的位移是由节点位移插值获得的, 通常插值的阶数由单元采用的节点数目决定, 具体分3种情况: 仅在角点处布置节点的单元, 见图 4(a)的8节点实体单元, 在每个方向上采用线性插值, 常常称它们为线性单元或一阶单元; 在每条边上有中间节点的单元, 见图 4(b)的20节点实体单元, 采用二次插值, 常常称它们为二次单元或二阶单元; 在每条边上有中间节点的修正三角形或四面体单元, 见图 4(c)的10节点四面体单元, 采用修正的二阶插值, 常称它们为修正单元或修正的二阶单元。

图  4  三维有限元单元

Figure  4.  Elements of 3D finite element

下载: 全尺寸图片 幻灯片

道面结构三维有限元分析常采用六面体实体单元进行模拟, 常用的六面体单元基本性质见表 4。

表  4  三维六面体单元的基本性质

Table  4.  Basic properties of 3D hexahedral elements

单元名称	单元类型	结点数/积分点数	位移形函数	优点	存在问题
C3D8	线性等参单元, 完全积分	8/8	一阶	计算成本低	剪切自锁, 精度较差
C3D8R	线性等参单元, 减缩积分	8/8	一阶	对位移的求解较精确, 弯曲时不易剪切自锁	沙漏
C3D8I	线性等参单元, 非协调模式	8/8	一阶	克服了剪切自锁, 在弯曲问题中计算成本降低	扭曲过大, 分析精度会降低
C3D20	二次等参单元, 完全积分	20/27	Serendipity二阶	对应力的计算很精确, 一般无剪切自锁	不能用于接触分析, 体积自锁, 弯曲自锁
C3D20R	二次等参单元, 减缩积分	20/8	Serendipity二阶	不会出现严重的沙漏问题, 对自锁问题不敏感	不能在接触分析中使用, 不适用于大变形问题

下载: 导出CSV 

| 显示表格

考虑到计算成本的原因, 将荷载区域网格密度划分为0.1 m×0.1 m, 考察不同单元类型对计算结果的影响, 见表 5。由表 5可知: 在同样的网格密度条件下, 计算沥青层顶的变形和应力时, 使用缩减积分单元要比线性积分单元计算的结果更加收敛, 20节点的单元计算结果并不比8节点单元计算结果有明显优势, 相反20节点由于增加了积分节点数, 使得CPU使用时间大幅增加; 在计算土基顶面的变形和应力时, 4种单元类型的计算结果相差不大, 主要因为模型沿厚度方向网格划分较疏, 在0.1 m×0.1 m大小网格情况下, 4种单元类型计算的土基顶面的力学指标相差不大。

表  5  不同单元类型数值计算结果

Table  5.  Numerical calculation results of different elements types

单元名称		C3D8	C3D8R	C3D8I	C3D20R
道面表面	竖向变形/mm	0.373 7	0.392 7	0.376 9	0.382 1
	竖向压力/MPa	-0.631 0	-0.650 9	-0.712 6	-0.801 0
土基顶面	竖向变形/mm	0.116 2	0.125 9	0.116 0	0.117 5
	竖向压力/kPa	-8.587	-8.626	-8.345	-9.715
整个CPU使用时间/s		164.7	131.7	235.6	2 185.2

下载: 导出CSV 

| 显示表格

要想获得更为精确的数值解, 除了水平向的单元大小控制外, 沿着厚度方向的单元大小也要合理控制, 综合分析得出在进行三维有限元模拟时, 不同的单元类型在同一网格密度条件下, 所得到的数值结果以C3D8R单元更精确, 同时CPU使用时间更少。

2.2   单元大小

有限元中单元的大小对计算精度会产生很大的影响, 单元过密会造成计算成本增加。为降低计算机时, 一般对荷载作用区域的网格密度进行细化, 以荷载作用区域为中心渐变增加网格的大小, 以减少单元的数量, 节约计算成本。采用不同的网格密度计算的结果见表 6。

表  6  不同网格密度计算结果

Table  6.  Calculation results of different mesh densities

单元大小/m		0.2×0.2	0.1×0.1	0.05×0.05
道面表面	竖向变形/mm	0.495 5	0.392 7	0.404 4
	竖向压力/MPa	-0.586 5	-0.650 9	-0.683 9
单元总数		17 408	33 282	69 696
整个CPU使用时间/s		53.5	131.7	381.7

下载: 导出CSV 

| 显示表格

由表 6可知: 单元大小不断细化, 由0.1 m×0.1 m变化到0.05 m×0.05 m时, 两者弯沉的变化在3%以内, 表明在单元尺寸细化到一定程度时, 弯沉对网格尺寸已经不很敏感, 同时该有限元软件是基于位移法而设计的, 位移收敛的速度要快于其他力学响应量; 对于表面应力, 随着单元逐步变小, 不断收敛, 单元大小由0.1 m×0.1 m细化到0.05 m×0.05 m时, 应力变化幅度为4.8%, 能够满足工程的需要。故建议在计算时荷载作用区域单元的大小取为0.1 m×0.1 m, 以荷载区域为中心逐步放大单元, 以节省计算资源。

3.   有限元模型验证

为了应对大飞机的超大荷载对机场道面带来的破坏, 并由此可能引发的飞机安全事故, FAA建立了国家机场道面试验中心(National Airport Pavement Test Facility, NAPTF), 致力于机场道面结构的研究。NAPTF位于大西洋城国际机场的威廉休斯技术中心, 通过足尺试验来分析大飞机对机场道面的影响。为了减少环境对足尺试验的影响, NAPTF设计为一个室内直线式加载试验中心, 试槽长度为274 m, 宽度为18.3 m, NAPTF在铺筑路面的同时, 在路面结构内部安装了大量的不同类型的传感器, 形成了一个综合的测试系统, 能够对路面结构在轮载作用下的响应进行准确测量, 测量包括湿度、温度、轮载引起的应力与应变及挠度等路面结构响应信息。

为了验证本模型的有效性, 选择中等强度土基的沥青稳定基层柔性道面(MFS)进行分析, 以B777作为作用荷载, 轮胎充气压力根据NAPTF的实测值取1.296 MPa^[14], 道面材料参数选取见表 7。

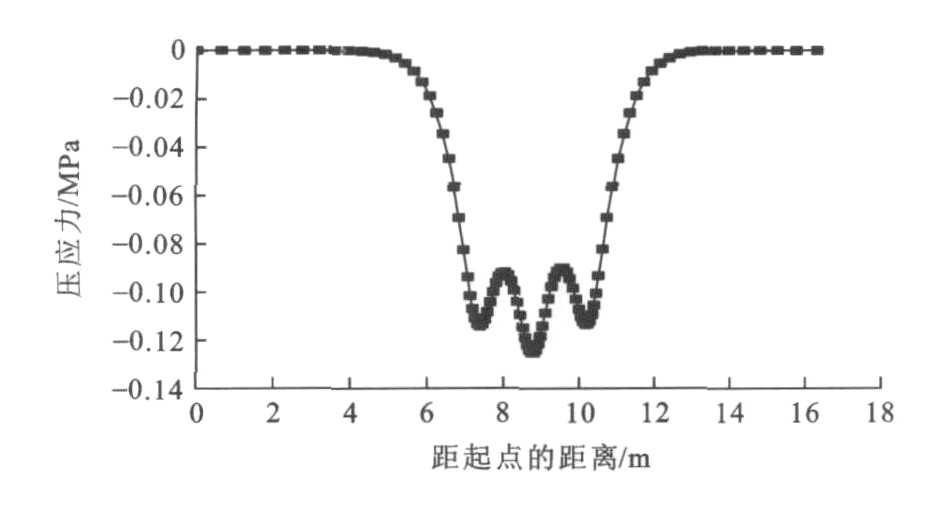
表  7  材料参数

Table  7.  Material parameters

结构层	厚度/cm	回弹模量/MPa	泊松比
沥青混凝土面层	12.7	8 963	0.35
沥青混凝土基层	12.4	8 963	0.35
级配碎石底基层	21.6	450	0.38
土基	258.1	55	0.40

下载: 导出CSV 

| 显示表格

采用本文所得出的三维有限元模型模拟NAPTF试验道面结构, 计算B777飞机静态荷载作用下道面结构力学响应, 得到的数值结果见图 5, 实测结果见图 6, 图 5、6中纵坐标为土基顶面竖向压应力。图形的变化趋势基本一致, 实测结果第1峰值要比第3峰值小, 而计算结果峰值关于中心对称, 且实测结果要比计算结果小50%, 主要因为实测数据是飞机轮载动荷载作用下道面结构的力学响应, 计算结果仅仅只考虑静态荷载作用, 同时也没有考虑材料的非线性特性。

图  5  有限元计算结果

Figure  5.  Calculation result of finite element

下载: 全尺寸图片 幻灯片

图  6  NAPTF实测数据

Figure  6.  Measured data of NAPTF

下载: 全尺寸图片 幻灯片

考虑以上因素, 综合本文有限元模型的数值结果, 本文的有限元计算模型在静态线弹性条件下对大型飞机荷载响应进行分析得到的应力、应变量是可靠的。

4.   结语

飞机轮载作用下道面结构的力学响应规律对道面结构性能预估的准确性至关重要, 建立三维有限元模型能够准确地获取轮载作用下道面结构的空间响应, 本文通过对有限元模型的边界条件、单元类型等进行分析, 得出以下结论。

(1) 利用通用有限元软件对沥青道面结构力学响应进行模拟, 考虑全起落架荷载作用时, 模型的几何尺寸宜为30 m×30 m×10 m(沿着飞机滑行方向、垂直飞机滑行方向、厚度方向), 约束水平方向的水平位移和模型底部的所有自由度, 采用tie连接模拟层间接触完全连续条件。

(2) 对比分析了常用三维六面体实体单元的优缺点, 结合计算分析结果和CPU使用时间, 得出了在进行沥青道面结构模拟时, 宜采用C3D8R单元。

(3) 采用C3D8R单元, 分别对0.2 m×0.2 m、0.1 m×0.1 m、0.05 m×0.05 m三种不同的荷载区域单元大小进行分析, 得出考虑位移指标时, 荷载区域的大小取0.1 m×0.1 m就可以, 需要考虑应力时, 荷载区域单元的大小需要0.05 m×0.05 m, 才能保证计算结果的收敛满足工程需要。

(4) 建立的道面结构三维有限元模型能够模拟B777-300、A380-800飞机荷载作用道面结构表面弯沉和土基顶面的竖向压应变的变化规律, 具有普遍的适用性。