Multi-level clustering algorithm for crack detection of concrete surface
-
摘要: 为了检测混凝土表面裂缝及其宽度, 对含有裂缝的数字图像进行k-均值聚类, 提取出所有疑似裂缝的像素点, 进行了二值化处理。根据像素点的位置关系, 提取连通分量, 将连通分量作为聚类对象, 构造连通分量间的距离函数。利用谱聚类算法将连通分量聚类, 根据裂缝特征, 去掉伪裂缝部分, 得到完整的裂缝对象, 并通过局部旋转算法对裂缝的宽度进行了2次数值计算。分析结果表明: 与Canny、Sobel算子比较, 多级聚类算法在裂缝提取时能去掉较多的噪声, 抗噪能力强; 通过局部旋转算法计算裂缝宽度时, 计算值与实际值的平均相对误差分别为3.86%、2.40%, 算法精度高, 适用于各种类型裂缝宽度计算。Abstract: In order to detect the crack and its width of concrete surface, the k-means clustering was applied for crack digital image, and binary image was got based on taking out entire suspected crack pixels from clustering results. The connected components of binary image were extracted according to the ubiety of pixels, the distance function of connected components was constructed considering connected components as clustering objects. Connected components could be clustered by spectral clustering algorithm, pseudo cracks were removed on the basis of crack features, and whole crack image was obtained. Numerical calculations of crack width were carried out twice by local rotation algorithm. Research result shows that multi-level clustering algorithm can get rid of more noises during extracting crack, and has stronger anti-noise ability compared with Canny operator and Sobel operator. When the crack width is calculated by local rotation algorithm, the average relative errors of calculated value and actual value are 3.86%and 2.40% respectively, so the algorithm has high accuracy and can be used for width calculations of all kinds of cracks.
-
Key words:
- pavement engineering /
- crack detection /
- image processing /
- k-means clustering /
- spectral clustering
-
0. 引言
随着经济的发展, 建造了大量的道路与桥梁, 而这些建筑物会随着时间出现许多裂缝, 过宽的裂缝不但影响建筑结构的外观, 而且会导致混凝土中钢筋锈蚀, 加速混凝土老化, 削弱建筑物的承载能力, 影响建筑物的正常使用。为了确保这些建筑物的使用安全, 必须对其进行定期检测, 从而涉及到结构表面裂缝及其宽度检测。
随着计算机的快速发展, 数字图像处理技术被广泛应用于土木结构的裂缝检测中[1-7]。Bhandarkar等利用计算机断层摄影技术对原木中的裂缝进行了检测[1]; Cheng等在裂缝检测中, 基于样本空间减少与插值方法对实时图像的阈值选取给出了一种方法[2]; 邹勤等把裂缝看作是最小生成树, 通过对最小生成树的提取来实现对裂缝的提取, 此方法适用于宽度较小的裂缝, 而且后续拼接裂缝会影响裂缝宽度的计算准确度[3]; 王兴建等针对路面裂缝的不同噪声构造了不同的去噪模型, 采用多级噪声模型对裂缝图像进行去噪处理[4]; Abdel-Qader等将快速Haar小波变换、快速傅立叶变换、Sobel与Canny算子4种边缘检测方法应用到桥梁裂缝识别过程中, 并对它们的识别效果进行对比, 得出了快速Haar小波变换比其他3种方法识别率高, 但是Haar小波变换算法对细微裂纹的检测效果较差, 影响裂缝的提取, 而且计算量较大[7-8]; 张宏等构造了一种智能算法, 大量的种子经随机游走后落入到缝内, 从而检测出图像中的裂缝[9]; 基于图像的裂缝宽度检测的研究还不多见, 查旭东等对连续配筋混凝土路面提出了一种测量裂缝宽度的算法, 它是一种几何算法, 用裂缝的面积与裂缝的长度之商作为裂缝的宽度, 该方法只能检测出整个裂缝的评价宽度, 无法得到每个截面的宽度[10]; 卢晓霞介绍了2种测量裂缝宽度的方法, 分别是水平左右边缘点法与垂线法, 这2种方法只是基于裂缝是垂直或水平走向的情形, 而裂缝的分布与走向往往是很复杂的[11]。
本文对混凝土裂缝检测提出了一种新的检测方法———基于聚类的检测方法, 该方法首先对拍摄到的裂缝图像进行k-均值聚类, 根据裂缝的颜色特征可知平均灰度最小的一类即为包含裂缝的图像, 然后二值化该图像, 并提取二值化图像中的连通分量, 根据裂缝的形态特征去掉含像素点少的连通分量(噪声), 最后定义剩余连通分量间的距离, 通过一个阈值, 将图像转化为一个拓扑图, 这样图像中裂缝检测问题就转化为图中最大团的检测问题, 利用谱聚类算法实现对裂缝的提取。本文对裂缝宽度检测也提出了一种新的算法———局部旋转法, 该方法把非垂直的裂缝通过公式进行旋转, 使其走向趋于垂直, 能适用于各种形式的裂缝。
1. 基于聚类的图像二值化
考虑到裂缝图像的的色彩信息不多, 首先将获取的图像转化为灰度图像, 再进行二值化处理。
1.1 k-均值聚类算法
对于一幅尺寸为m×n的彩色图像(已归一化), 它的红、绿、蓝三层矩阵记为R、G、B, 记
F中所有像素点si集合记为
对S中N个对象划分成k个集合, 分别为K1、K2、…、Kk, 其中k需要提前给出。聚类所得的集合满足
对于任意的si, 根据“距离”来判断它属于Kj中的哪一个类, “距离”通常取欧氏距离。具体算法流程如下。
Step 1:输入需要聚类的数目k与对象集S。
Step 2:任意选取k个数(在对象集S中选取)作为k个初始聚类中心。
Step 3:将对象集S中的元素按照最小距离原则分配到最邻近聚类。
Step 4:使用每个聚类中的样本均值作为新的聚类中心。若新的聚类中心与旧的聚类中心不相等, 转Step 2, 否则, 结束。
Step 5:输出k个聚类。
1.2 图像二值化
在实际拍摄裂缝图像的过程中, 裂缝及其背景往往很复杂。通常裂缝比较深或背景色偏亮的时候, 裂缝的灰度值与背景色相比要偏暗, 这样聚很少的类就能得到较理想的目标图像, 但是当裂缝很浅或背景色很暗的时候, 在聚的类多的情况下才能得到比较好的裂缝图像, 并且当对图像聚类的时候, 如果聚的类少, 不足以得到理想的裂缝粗略图, 但是当聚的类较多时, 得到的图像中裂缝会断掉很多, 所以聚的类数很重要, 图像聚的类数因图而异。
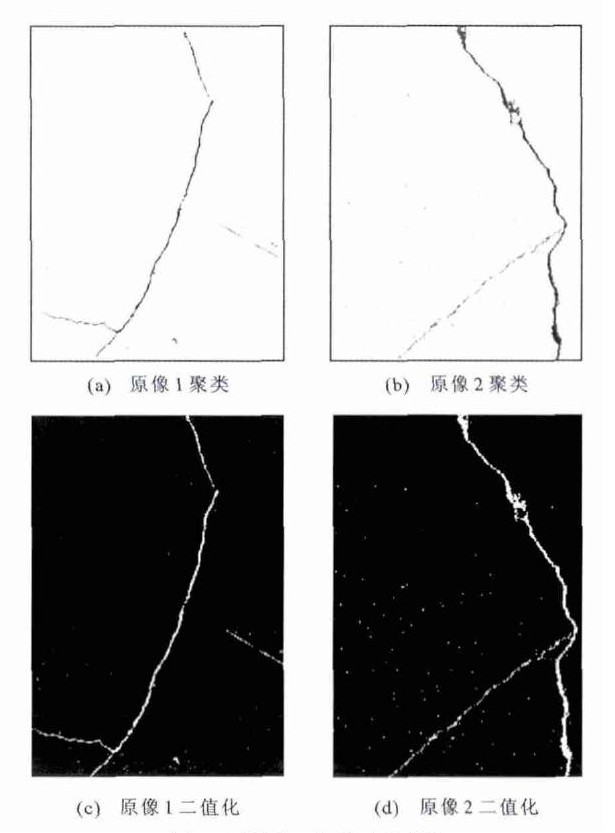
本文对两幅带裂缝的图像(图 1)采用上述聚类算法进行计算, 结果见图 2。
图 1(b)与图 1(a)相比较, 易看出图 1(b)中的裂缝要比图 1(a)清晰, 也就是图 1(b)的裂缝与背景色对比程度较大。根据裂缝自身灰度偏暗的特点, 可知裂缝一般会被划分到整体均值小的类中。经过试验, 可以得到图 1(a)聚五类与图 1(b)聚三类最合适, 然后从所得的聚类中提取均值最小的一类即为所求, 见图 2(a)、(b), 再把图 2(a)、(b)中所有灰度值小于1的点赋值为1, 其余为0, 即二值化, 见图 2(c)、(d)。
由于聚类后的图像除了裂缝外还有很多的“噪声”, 想要得到干净的裂缝, 就必须去掉这些“噪声”, 提取出清晰完整的裂缝, 对此, 本文采用谱聚类算法。
2. 基于谱聚类的裂缝提取算法
对于不同的图像, 细提取时算法一般不一样, 即使算法步骤一样, 但阈值的选取通常情况下也不同, 这是因为在用聚类粗提取裂缝的过程中, 得到的裂缝图像是多样的, “噪声”也是多样的, 本文只叙述主要的算法步骤。
首先对二值化后的图像提取连通分量, 此连通分量记录的是灰度值为1的像素点的位置。给一阈值, 把像素点少的连通分量去掉, 其目的是将图像中小的“噪声”去掉, 然后记剩下的连通分量集合为
zu为一个连通分量, 计算这q个连通分量之间的距离, 距离矩阵D与邻接矩阵A分别为
式中: d(P1, P2)为平面两点P1、P2间的欧氏距离。
当2个连通分量间的距离(duv)小于阈值δ时, 就认为连通分量zu与zv相连, 否则不相连。阈值δ的选取规则如下: 对所有的duv(第u个连通分量与第v个连通分量的距离, u < v), 按从小到大的顺序排列, 取其第q+1个数或稍大的数, q为连通分量个数。
由于裂缝上的连通分量两两相连, 如果从图论角度来描述, 裂缝上的对象(连通分量)是连通的。规定2个连通的对象都相连, 并设其邻接矩阵为
由A产生
Step 1:A(1)=A, t=1, t为迭代步数。
Step 2:A(t+1)=A(t)A, 同时更新A(t+1)的非零元素为1。
Step 3:如果A(t+1)≠A(t), t=t+1, 转Step 2, 否则A=A(t+1), 结束。
按邻接矩阵
利用谱聚类[12-14]就可以将连接紧密的对象聚成一个类, 最大的一个类即为裂缝上的所有连通分量, 从而检测出图像中的裂缝。谱聚类算法如下: 求出
P的非零分量对应的序号即为所求的连通分量的序号, 这些连通分量就构成整条裂缝。
在图 2的基础上, 通过上述计算就可以检测出裂缝的连通分量, 计算结果见图 3。
3. 算法比较
与其他检测算法(Canny、Sobel算子)比较, 本文算法能很好地保存裂缝的特征信息, 有利于裂缝的提取, 图 4是用Canny、Sobel算子处理图 1(b)得到的图像。从图 4中看出, 本文算法(图 2(b))优于Sobel算子与Canny算子, 特别是Canny算子, 几乎把裂缝的所有信息都遗失了。
为了更好地说明试验效果, 本文选取了一背景比较复杂的图像进行对比, 能准确检测出裂缝位置, 检测过程见图 5。从图 5(a)中不难看出, 裂缝的背景很复杂。通过k-均值聚类提取出裂缝的基本轮廓并二值化后得到图 5(b), 图 5(b)与图 5(c)对比可知, 本文方法在粗提取裂缝时能去掉较多的噪声, 对后续工作的进展有利。由于图 5(b)中的背景有很多的噪声, 本文先用文献[9]中的连通分量过滤算法得到图 5(d), 其中还有一些非裂缝连通分量, 再根据本文谱聚类方法, 能很好地把裂缝提取出来, 见图 5(e)。
图 5 复杂背景裂缝检测过程及方法对比Figure 5. Process of crack detection with complicated background and method comparison4. 裂缝宽度计算
在裂缝宽度检测时, 需要确定曲线在某一截面的宽度, 当给定的裂缝是水平(或垂直)方向的直线时, 其宽度就是截面所在位置的列(或行)的像素个数, 但在实际裂缝宽度检测时, 裂缝曲线的形态很复杂, 通常都是倾斜或弯曲的曲线, 这时裂缝的宽度就不再是截面所在位置的列(或行)的像素个数, 对于这种问题, 可以采取局部旋转法来解决。
为了检测裂缝宽度, 根据本文算法, 首先要确定裂缝所在曲线在每一个截面的法线方向, 由于裂缝曲线是由一些互相邻接的目标像素点组成, 从微观上看是有宽度并且是锯齿形的, 而数学中描述的曲线是没有宽度的, 所以不宜通过求导数或差分等方法确定曲线的走向, 本文将利用裂缝像素的坐标通过最小二乘法来确定裂缝截面的法线方向。
4.1 裂缝截面法线方向的确定
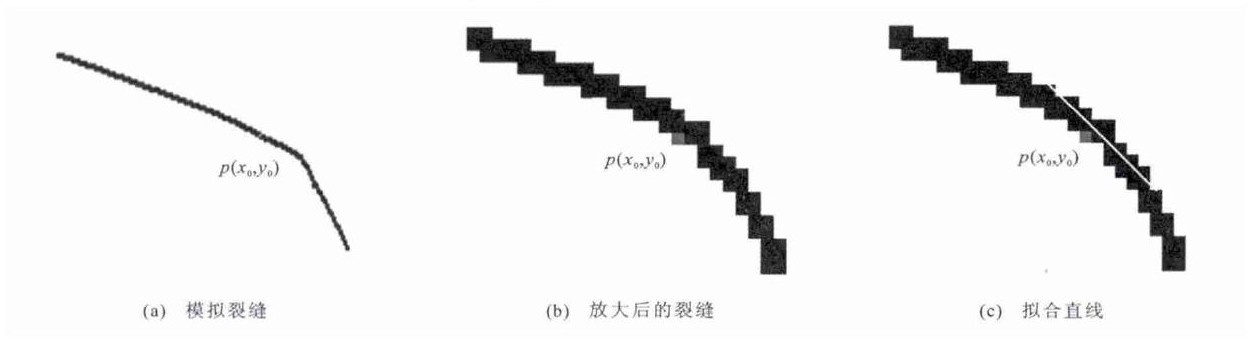
在图 6(a)中, 设p(x0, y0)为裂缝上的一点, 裂缝曲线在该点的法线与x轴正向的夹角为θ, 为便于描述, 从图像中取出一个包含p(x0, y0)的子图进行放大(图 6(b)), 再在该子图中取出以p(x0, y0)为中心的N′×N′的子块T, 子块T内裂缝像素点占到20%左右, 并记录所有裂缝像素点坐标(xe, yf), 以T的左上角为(1, 1), 向下为x轴正向, 向右为y轴正向。对这些点进行线性拟合, 得到一条直线l(图 6(c)), 这样, 经过p(x0, y0)点且与直线l垂直的直线即为裂缝曲线在点p(x0, y0)的法线。
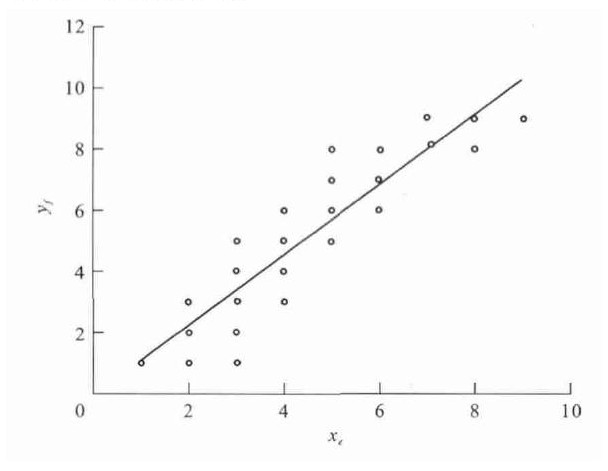
以图 6(c)为例, 取N′=9, 子块内共有25个黑点, 其坐标见表 1。
表 1 裂缝像素点坐标Table 1. Coordinates of crack pixels
对这些点做最小二乘拟合, 得到直线l的斜率为1.148 1, 见图 7。
4.2 裂缝宽度检测
首先从裂缝图像中(图 6(c))取出一个以p(x0, y0)为中心的N′×N′的子块T, 确定出曲线在该点的法线方向θ(法线与x轴不大于
设旋转前的坐标为(x, y), 旋转后的坐标为(X, Y), 则有
由式(1), 对于旋转后的图像T′上的一个像素点Q(X, Y), 其灰度值等于T中点(x, y)的灰度值, 其中
显然, 式(2)计算的结果一般不是正整数值, 无法对应到T中的一个像素点, 这里采用最近像素点赋值法, 即用T中离(x, y)最近的像素点的灰度值给T′上的像素点Q(X, Y)赋值。这样, 子块T经旋转后在点p(x0, y0)的局部范围内就是一条垂直的线段E, 由于p(x0, y0)是旋转时的不动点, 所以T′上的点p(x0, y0)对应行的像素个数就是该点的裂缝宽度, 但由于旋转过程存在计算误差, 可以用垂直线段E上各截面的宽度(加权)平均作为p(x0, y0)点的裂缝宽度。
以图 6(c)为例, 由于直线l的斜率为1.148 1, 所以sin(θ)、cos(θ)分别为0.656 8、0.754 1, 子块T经旋转后的图像见图 8。这样p(x0, y0)的像素宽度为2, 由于裂缝曲线比较复杂, 旋转时可能有误差, 所以可用p(x0, y0)点上下若干个行的像素宽度的平均值作为p(x0, y0)点的像素宽度。
利用上述算法, 可以计算出裂缝每一个截面的宽度, 这样就可以得到整条裂缝的平均宽度
4.3 数值试验
为了验证本文算法, 采集了2个带裂缝的混凝土图像, 见图 9, 图 9(a)实际测量了13个裂缝截面的宽度并记录了每个截面中心坐标(表 2), 图 9(b)实际测量了10个裂缝截面的宽度并记录了每个截面中心坐标(表 3), 根据尺子尺寸及其对应的像素个数可以求出图 9(a)、(b)每个像素对应的实际尺寸分别为0.185 mm×0.185 mm、0.313 mm×0.313mm。试验采用本文算法对图像进行处理, 并获取裂缝目标, 利用局部旋转算法计算出每个截面的宽度, 结果见表 2、3。
通过比较计算宽度与实际测量宽度, 图 9(a)其平均误差为0.05mm, 平均相对误差为3.86%, 图 9(b)其平均误差为0.10mm, 平均相对误差为2.40%, 算法精度基本达到实际应用的要求。从计算结果可见, 个别截面的误差还比较大, 如表 2中第10个, 表 3中第2个, 其主要原因是在裂缝检测时二值化过程造成的, 显然, 二值化时阈值的大小直接影响裂缝的宽度。此外, 在裂缝检测时还涉及对图像的腐蚀、膨胀等操作, 这也会影响裂缝的计算宽度, 所以, 本实例出现的误差主要产生于裂缝检测过程。总体来说本文的裂缝宽度检测算法精度较高。现有的一些裂缝宽度检测算法对本算例都不适应, 文献[10]通过估计裂缝长度来计算裂缝的平均宽度, 文献[11]只适用于水平或者垂直走向的裂缝。
5. 结语
对裂缝图像的检测与裂缝宽度的计算, 由于裂缝图像背景的复杂性, 通常找不到一种通用的方法来解决所有的裂缝检测问题, 本文算法一定程度上解决了裂缝检测及其宽度计算问题。对图像进行二值化处理是裂缝检测的基本环节, 本文利用k-均值聚类对图像进行二值化, 通过对连通分量的过滤, 实现裂缝粗提取; 由于二值化步骤造成裂缝的断裂, 为此, 对连通分量进行谱聚类, 实现对裂缝的拼接与提取; 在计算裂缝宽度时, 由于计算机读取图像的时候是把图像离散成了一个个小块, 成像时就存在着一定的误差, 二值化步骤也对裂缝宽度造成了误差。为了提高裂缝宽度检测的精度, 需要综合考虑检测出来的裂缝与原始图像在裂缝及其边缘处的灰度; 为了提高算法的适应性, 对算法中的参数还有待做进一步的优化。
-
图 5 复杂背景裂缝检测过程及方法对比
Figure 5. Process of crack detection with complicated background and method comparison
-
[1] BHANDARKAR S M, LUO Xing-zhi, DANIELS R, et al. Detection of cracks in computer tomography images of logs[J]. Pattern Recognition Letters, 2005, 26(14): 2282-2294. doi: 10.1016/j.patrec.2005.04.004 [2] CHENG H D, SHI X J, GLAZIER C. Real-time image thresholding based on sample space reduction and interpolation approach[J]. Journal of Computing in Civil Engineering, 2003, 17(4): 264-272. doi: 10.1061/(ASCE)0887-3801(2003)17:4(264) [3] 邹勤, 李清泉, 毛庆洲, 等. 利用目标点最小生成树的路面裂缝检测[J]. 武汉大学学报: 信息科学版, 2011, 36(1): 71-75. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201101017.htmZOU Qin, LI Qing-quan, MAO Qing-zhou, et al. Targetpoints MST for pavement crack detection[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 71-75. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201101017.htm [4] 王兴建, 秦国锋, 赵慧丽. 基于多级去噪模型的路面裂缝检测方法[J]. 计算机应用, 2010, 30(6): 1606-1609, 1612. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201006051.htmWANG Xing-jian, QIN Guo-feng, ZHAO Hui-li. Pavement crack detection method based on multilevel denosing model[J]. Journal of Computer Applications, 2010, 30(6): 1606-1609, 1612. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201006051.htm [5] 段跃华, 张肖宁, 李智, 等. 基于工业CT的混凝土集料二维及三维轮廓表征方法[J]. 中国公路学报, 2011, 24(6): 9-15. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201106004.htmDUAN Yue-hua, ZHANG Xiao-ning, LI Zhi, et al. Methods about digital representation on surface profile of concrete aggregates from 2-D to 3-D based on X-ray computed tomography[J]. China Journal of Highway and Transport, 2011, 24(6): 9-15. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201106004.htm [6] 万成, 张肖宁, 贺玲凤, 等. 沥青混合料动态模量数值预测方法[J]. 中国公路学报, 2012, 25(4): 16-28. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201204003.htmWAN Cheng, ZHANG Xiao-ning, HE Ling-feng, et al. Numerical prediction method for dynamic modulus of asphalt mixture[J]. China Journal of Highway and Transport, 2012, 25(4): 16-28. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201204003.htm [7] ABDEL-QADER I, ABUDAYYEH O, KELLY M E. Analysis of edge-detection techniques for crack identification in bridges[J]. Journal of Computing in Civil Engineering, 2003, 17(4): 255-263. [8] ROSALES M B, FILIPICH C P, BUEZAS F S. Crack detection in beam-like structures[J]. Engineering Structures, 2009, 31(10): 2257-2264. [9] ZHANG Hong, DONG An-guo, XU Zhi-gang, et al. Seeds moving algorithm and its application on bridge crack detection[C]//IEEE. 2010 3rd International Conference on Power Electronics and Intelligent Transportation System. Shenzhen: IEEE, 2010: 270-274. (in Chinese). [10] 查旭东, 王文强. 基于图像处理技术的连续配筋混凝土路面裂缝宽度检测方法[J]. 长沙理工大学学报: 自然科学版, 2007, 4(1): 13-17. https://www.cnki.com.cn/Article/CJFDTOTAL-HNQG200701002.htmZHA Xu-dong, WANG Wen-qiang. The testing method of crack width for continuously reinforced concrete pavement based on image processing technique[J]. Journal of Changsha University of Science and Technology: Natural Science, 2007, 4(1): 13-17. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HNQG200701002.htm [11] 卢晓霞. 基于图像处理的混凝土裂缝宽度检测技术的研究[D]. 成都: 电子科技大学, 2010.LU Xiao-xia. Concrete crack width detection technology based on image processing[D]. Chengdu: University of Electronic Science and Technology of China, 2010. (in Chinese). [12] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//University of California Press. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press, 1967: 281-297. [13] 田铮, 李小斌, 句彦伟. 谱聚类的扰动分析[J]. 中国科学E辑: 信息科学, 2007, 37(4): 527-543. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200704004.htmTIAN Zheng, LI Xiao-bin, GOU Yan-wei. Perturbation analysis of spectral clustering[J]. Science in China Series E: Information Sciences, 2007, 37(4): 527-543. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200704004.htm [14] REGE M, DONG Ming, FOTOUHI F. Bipartite isoperimetric graph partitioning for data co-clustering[J]. Data Mining and Knowledge Discovery, 2008, 16(3): 276-312. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 638
- HTML全文浏览量: 130
- PDF下载量: 1338
- 被引次数: 0
