Optimization model of urban parking fare based on equilibrium flow
-
摘要: 基于随机用户平衡原则, 分析了出行者的路径选择和停车选择行为, 建立了满足Logit关系的城市道路停车流量分配模型。基于收益管理思想, 以停车收益最大为决策目标, 建立了城市停车费用的双层规划模型, 并以7个节点和2个停车场的小型网络进行实例验证。分析结果表明: 当停车需求为10 000pcu·h-1时, 随着停车场2停车费用的提高, 停车流量不断向停车场1转移, 停车场1在停车费用不变的情况下收益不断增加, 当停车场2的停车费用为4元·h-1时, 总的停车收益达到最大; 当停车需求为20 000pcu·h-1时, 随着停车费用的上升, 总的停车收益将持续增加; 2个停车场之间存在博弈关系, 停车费用存在纳什均衡点, 当停车需求为10 000pcu·h-1时, 2个停车场的最优停车费用均为5元·h-1; 当停车需求为20 000pcu·h-1时, 2个停车场的最优停车费用均为最高限价10元·h-1。Abstract: Based on stochastic user equilibrium principle, the route choice and parking choice behaviors of travelers were analyzed, and the urban road parking assignment model meeting the logit relation was set up.Based on the revenue management ideology, the maximum parking revenue was taken as decision target, the bi-level programming model of urban parking fare was set up, and the example verification was carried out by using a small-size network with 7 nodes and 2 parking plots.Analysis result shows that when parking demand is 10 000 pcu·h-1, the parking flow will continue to shift from parking plot 2 to parking plot 1 with the increase of parking fare of plot 2, the parking revenue of parking plot 1 increases unceasing though its fare has no change.The total parking revenue reaches the maximum value when the parking fare of plot 2 is 4 yuan·h-1.When parking demand is 20 000 pcu·h-1, the total parking revenue will continue to increase with the increase of parking fare.On the other hand, the game relation exists betweenthe two parking plots and there is a Nash equilibrium point.In the case of 10 000 pcu·h-1, the optimal fare is 5 yuan·h-1 for the two parking plots, while the optimal fare is ceiling price 10 yuan·h-1 in the case of 20 000 pcu·h-1.
-
Key words:
- traffic planning /
- parking fare /
- bi-level programming /
- revenue management /
- user equilibrium
-
0. 引言
近年来, 随着中国经济的快速发展, 城市交通需求激增, 导致出行汽车化趋势明显。在这种条件下, 国内一些城市产生了道路交通拥堵, 进而带来了城市停车问题。尽管一些学者从不同角度对城市停车问题进行了分析和探讨, 包括停车设施规划、停车交通诱导及停车的交通影响评价等[1-5], 但对于城市停车收费问题的研究相对较少。从经济学角度来说, 城市停车资源是一种不可存储的服务商品, 在短期内, 提供这种商品的固定成本无法随着停车流量的增加而明显变化, 而城市停车需求却在不同的时间段与不同类型的停车设施(停车场) 之间存在很大差别, 因此, 利用差别化停车收费政策来改变出行行为是平衡停车需求与有效缓解城市道路交通拥堵的重要手段之一。
通常, 在制定停车收费价格时, 首先需要明确的问题是停车收费与停车需求之间的相互关系。目前, 相关学者对城市停车需求问题进行了研究, Gur等分析了非拥挤条件下道路交通和停车需求的分配问题, 并采用平衡分配理论对上述分配问题进行建模和分析[6]; Phansak将交通需求分为2类, 即拥有停车许可和随机停车, 对不同类别的出行者构造了相应的停车综合配流模型, 并以麦迪逊科尔中心的篮球比赛为例对模型和算法进行了验证和分析[7]; 严海等考虑了特殊条件下的停车配流问题, 构造了交通选择Logit模型[8]; 田琼等研究了多种交通方式的停车换乘问题, 建立了基于Logit随机均衡的停车换乘模型[9]。上述研究大多没有考虑出行者路径选择和停车选择的组合配流问题。事实上, 出行者在出行中会同时考虑这2个问题, 且两者之间存在相互关联。有些学者将这2个问题结合起来研究, 李志纯等同时考虑了出行者对路径和停车设施的选择问题, 基于用户平衡理论提出了等价的数学优化模型, 并采用增广Lagrange对偶算法进行求解[10]; 四兵锋等考虑了停车能力与道路能力限制等因素, 提出了具有能力约束的停车流量分配的平衡模型, 并采用乘子法进行求解[11]。上述2个研究均假设出行者对各类停车设施具有完全相同的信息, 即满足确定性的用户平衡条件, 而在实际中, 这种假设显然存在不足, 出行者的停车选择行为总会受到一些具有不确定性因素的影响。同时, 上述相关研究均没有考虑差别化停车收费对停车需求的影响与在此基础上的停车收费优化问题。
收益管理是20世纪70年代美国联邦政府取消民航管制后发展起来的管理科学的一个分支, 主要适用于服务性行业。40多年来, 收益管理已广泛应用在航空、酒店、租车、旅游、电网等管理中, 成为发展现代服务业最重要的工具。差别化定价、存量控制、超售及需求预测构成了收益管理理论的主要内容[12], 其中差别化定价针对具有不同价格弹性的需求实施差别定价, 以最大限度地增加收益。国外学者在此方面进行了大量研究, Gallego等提出了产品综合定价模型, 并建立了网络定价的随机模型, 采用相应的确定性模型求解网络定价问题[13-14]; Feng等提出了一般需求函数下的两级价格模型, 并基于最大凹向包络理论建立了价格和存量的综合优化模型[15-16]; Zhang等研究了考虑产品具有可替代性的多资源定价模型, 并给出了求近似最优解的算法[17]。而在中国, 收益管理的应用处于起步阶段, 主要运用于航空售票业、酒店管理等方面, 在服务业其他领域的推广和运用还不是很深入。
本文把收益管理思想引入到城市停车收费管理的问题中, 通过分析停车选择行为, 运用离散选择模型对城市停车在不同时间、不同停车设施之间的停车流量分配问题进行建模。在此基础上, 分析停车费用对于停车流量分配的影响, 运用双层规划模型研究不同时段、不同停车设施的停车收费优化方法, 以引导停车流量的分配模式, 从而实现停车资源的合理利用。
1. 停车行为建模
停车行为是指出行者在驾车终点附近寻找并选择停车的个体行为。通常, 出行者驾车从起点到终点后, 可以在多个停车场进行停车, 同时, 在起点到不同停车场之间存在多条路径。显然, 出行者的停车行为包含3方面: 从起点到停车场之间的路径选择、停车选择以及从停车场到目的地的步行过程。
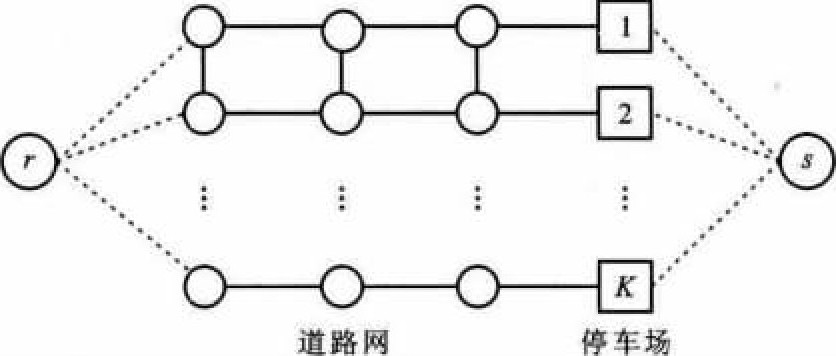
假设出行者从起点r出发驾车去终点s, 而目的地附近有K个停车场可供其选择, 从起点到达停车场k (k=1, 2, …, K) 之间存在多条路径, 停车选择过程见图 1。
从图 1可以看出, 停车选择和路径选择之间存在多种组合方式。假定某区域内起点r与终点s之间有K个停车场可供选择, 在t时段出行从起点r到终点s选择停车场k的广义费用Crskt为

式中: μrkt为t时段内出行者从起点r到停车场k的道路出行时间; pkt为t时段内停车场k的收费; tkt为t时段内出行者在停车场k中找到停车位的时间, 与停车流量有关; wks为出行者从停车场k到终点s的步行时间; εrskt为t时段内出行者从起点r到终点s途经停车场k的随机费用; α、β、γ均为参数。
随机费用是由出行者的选择行为产生的, 主要分为2方面: 出行者对出行费用判断的随机性, 即由于出行者自身对确定性费用的估计偏差所产生; 系统产生的随机费用, 即由于出行者的选择行为偏好受到其他出行者的影响所产生。通常, 能够获取更多、更及时的停车信息的出行者的随机误差要小于得不到停车信息的出行者的随机误差。
从式(1) 可以看出, 广义停车费用为随机变量, 显然, 停车选择问题本质上是概率问题。根据消费者行为理论, 某停车场的选择概率就是其广义费用在所有可供选项中最小的概率, 即

式中: Prskt为t时段出行者从起点r到终点s选择停车场k的概率。
假定随机误差项εrskt互相独立并且服从双指数分布, Prskt可以表示为Logit形式, 即

式中: θ为待定参数。
2. 城市停车流量分配模型
令qrst为t时段内出行者从起点r出发到终点s的驾车出行需求, qrskt为qrst中选择停车场k的需求, 则有

不失一般性, 本文假定出行者的路径选择满足Wardrop用户平衡条件, 即

式中: crkpt为t时段内出行者从起点r到停车场k的第p条路径上的出行时间; frkpt为t时段内从起点r到停车场k的第p条路径上的流量。
在图 1的停车选择过程中, 出行OD需求、路径流量与停车流量的关系为

式中: xat为t时段内路段a上的流量; δaprk为路网中路段与路径间的关联系数, 若路段a属于r到k之间的路径p, δaprk取值为1, 否则为0。
令tat为t时段路段a上的行驶时间, 通常可以表示为xat的单调递增函数为tat (xat), 根据路径与路段的关联性, 有

基于以上分析, 本文构造了描述城市道路网络中不同时段OD需求在不同停车设施与路径之间的分配问题的数学模型, 即

约束条件在式(6)、(7) 的基础上增加1个新的约束条件

式中: Z为目标函数; x为单位流量。
3. 基于收益管理的城市停车收费优化模型
根据前面的分析, 停车场在某个时段的停车收费是出行者广义费用中的一部分, 是停车流量分配模型中的一个参变量, 显然, 停车收费的变化会影响到各个时段的停车流量在各个停车场之间的分配状况, 因此, 停车收费与停车需求之间存在某种关系, 可通过数学优化模型来进行描述。停车收益最大化是指通过不同时段、不同停车场的差异化收费, 使得在研究时间和空间内所有停车场的总收益达到最大。
本文用双层规划模型来描述停车收益管理问题, 即: 下层模型描述出行者基于费用最小化的停车选择问题, 满足用户平衡条件; 上层模型描述如何制定最佳的停车收费, 以实现停车收益最大化。如果可得到双层规划问题的最优解, 则出行者和管理者的利益将同时满足。本文提出的双层规划模型中的上层模型为

下层模型的目标函数可由Z代替, 约束条件中, 式(11) 不变, 其他2个条件更新为

式中: pmax为出行者所能接受的最高停车费用; Ck为停车场k的运营成本; qrskt (pkt) 为停车流量qrskt和停车费用pkt之间的隐函数。
约束条件(13) 表示任意时段、任意类型停车设施的停车收费不可以超过政府规定的最高上限; 约束条件(14) 表示确定停车费用后, 各时段、各类停车设施的停车收益不少于其运营成本。
4. 求解算法
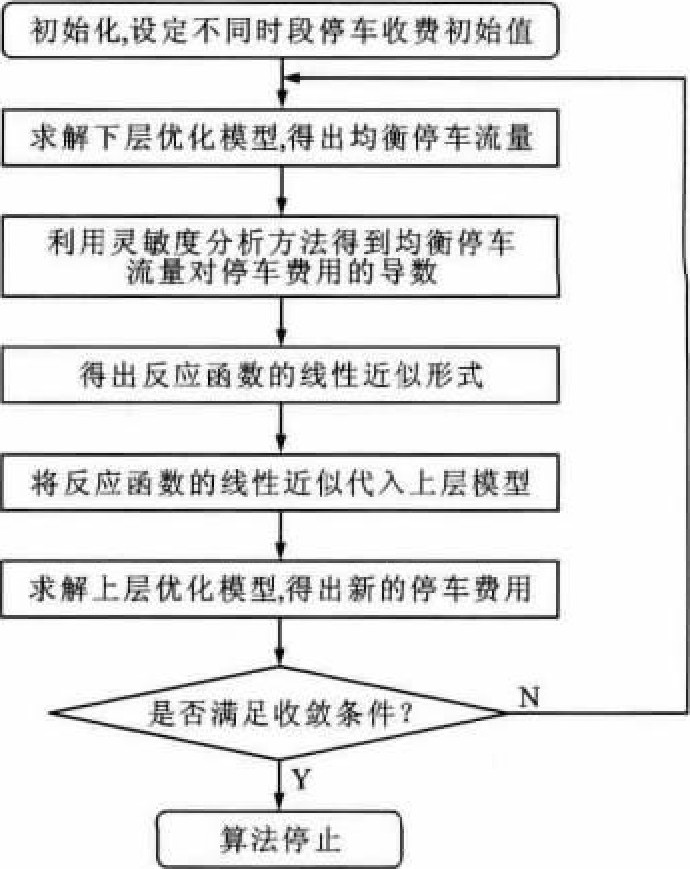
在本文提出的双层规划模型中, 确定停车流量qrskt和停车费用pkt之间的映射关系qrskt (pkt) 是求解上述双层规划模型的关键, 可采用灵敏度分析方法得出各个时段、各个类型停车需求对停车收费的定量关系, 然后, 再应用泰勒展开式进行线性近似, 从而将双层优化问题转换为单层优化问题以求解[18-19], 算法流程见图 2。
5. 计算结果分析
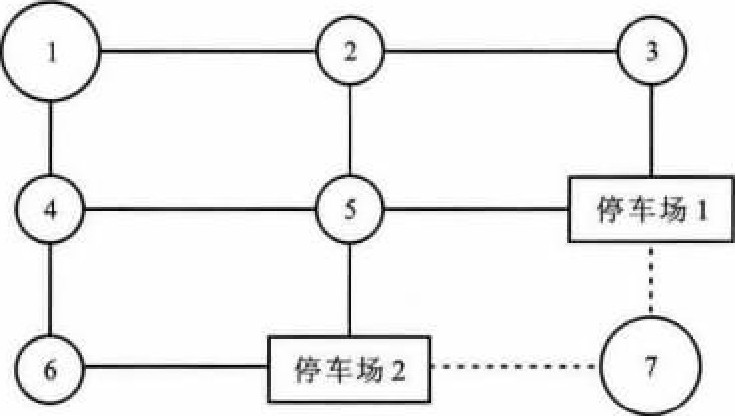
本文通过简单算例来说明本文模型及算法的有效性, 算例路网中包括1个OD对、2个停车场、9条道路和2个步行路段。假定停车场1、2分别为路内和路外停车场, 网络结构见图 3, 节点1与7分别为起点与终点。
本文采用BPR形式的路段阻抗函数, tat (xat) 可表示为

式中: ta0为路段a上的零流阻抗; Va为路段a上的通行能力; α1与α2分别为待定参数, 本文分别取为0.15和4.00。
路段a上的路段零流阻抗ta0与路段通行能力Va的取值(简称为路段数据) 见表 1。
表 1 路段参数Table 1. Road section parameters
通常, 停车时间与停车流量有关, 并受到停车设施供给能力的限制, t时段内在停车场k的停车延误tkt (qkt) 为[20-21]

式中: tk0为停车流量为0时, 出行者在停车场k中找到停车位的时间; Hk为停车场k的停车能力; qkt为在时段t内出行者选择停车场k的总停车流量。
假定停车场1距离目的地(节点7) 较近, 停车场2距离目的地较远, 2个停车场的停车能力均为8 000pcu, 停车场相关数据见表 2。
表 2 停车场参数Table 2. Parameters of parking plots
下层模型中的相关参数θ、α、β、γ分别取值为1、0.5、1、1。为便于分析, 分停车高峰和停车平峰2个时段进行计算。假设平峰时段从起点到终点的出行需求为10 000pcu·h-1, 高峰时段从起点到终点的出行需求为20 000pcu·h-1。在上层模型中, 假定pmax为10元·h-1, Ck为2 000元。
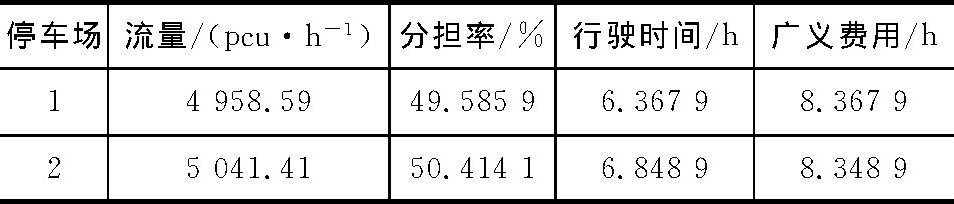
表 3为平峰时段的不同路段均衡流量与阻抗的计算结果, 表 4为在相同条件下停车场1、2的停车流量、分担率、道路行驶费用以及停车广义费用的计算结果。
表 3 不同路段的计算结果Table 3. Calculation results for different road sections 表 4 不同停车场的计算结果Table 4. Calculation results for different parking plots
表 4 不同停车场的计算结果Table 4. Calculation results for different parking plots
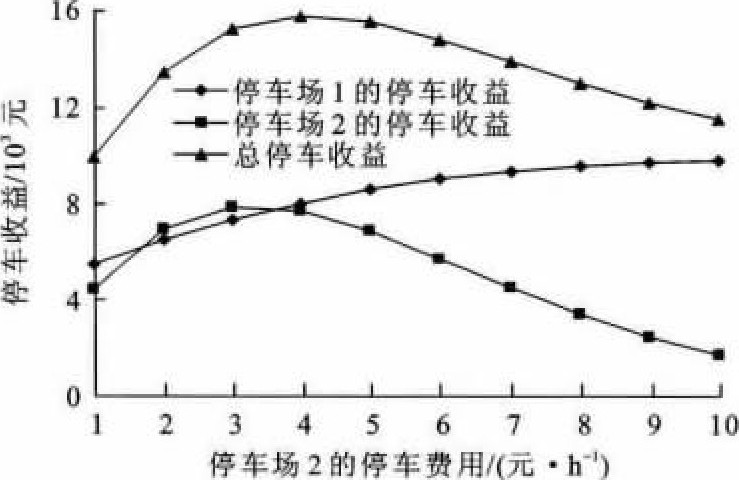
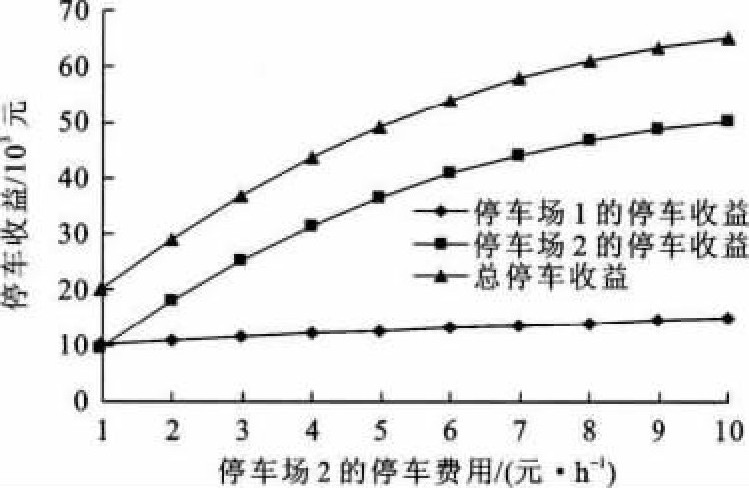
首先分析停车收益随停车费用的变化情况。当停车场1的停车费用为2元·h-1保持不变, 停车场2的停车费用从1元·h-1变化到10元·h-1时, 图 4、5分别为在平峰时段和高峰时段不同停车收益的变化情况, 从中可以看出, 在平峰时段, 随着停车场2停车费用的上升, 停车流量不断向停车场1转移, 使停车场1在费用不变的情况下收益不断增加, 而停车场2的收益在其费用为3元·h-1时达到最大值, 其后由于停车流量的减少而降低, 当停车场2的费用为4元·h-1, 2个停车场的总收益达到最大值。而在高峰时段, 随着停车场2停车费用的上升, 2个停车场的停车收益均不断增加, 总收益也随之不断增加, 这是由于高峰时段停车流量大, 超过了停车场的供给能力, 停车费用的上升对停车流量分配的影响相对较小, 因此, 2个停车场的停车收益均随着停车费用的上升而增加。
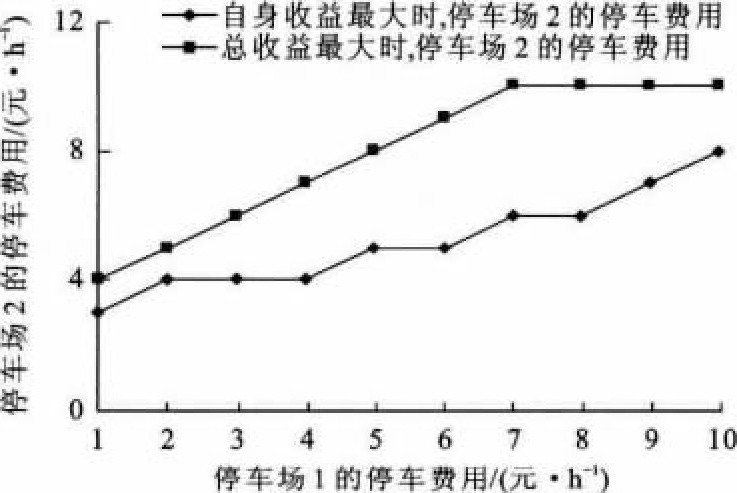
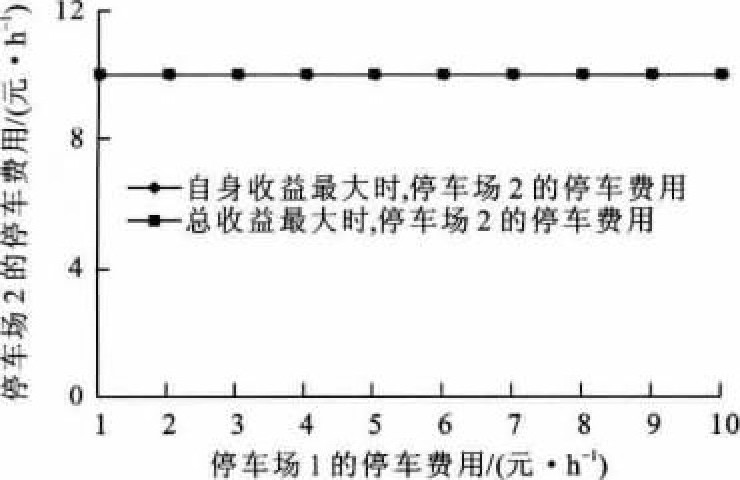
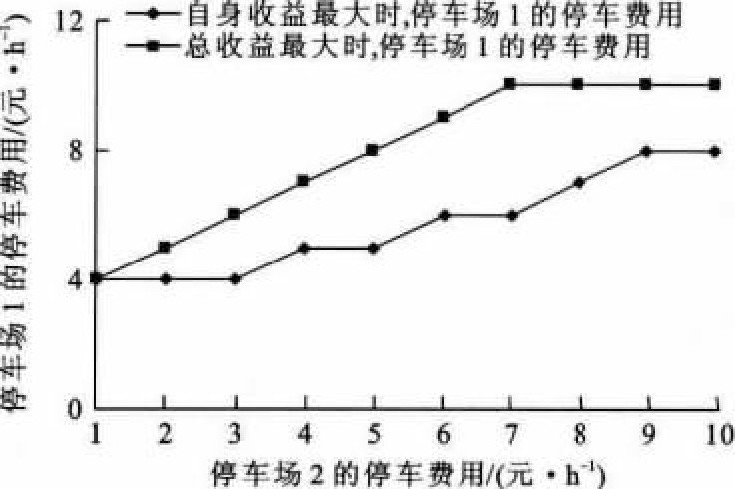
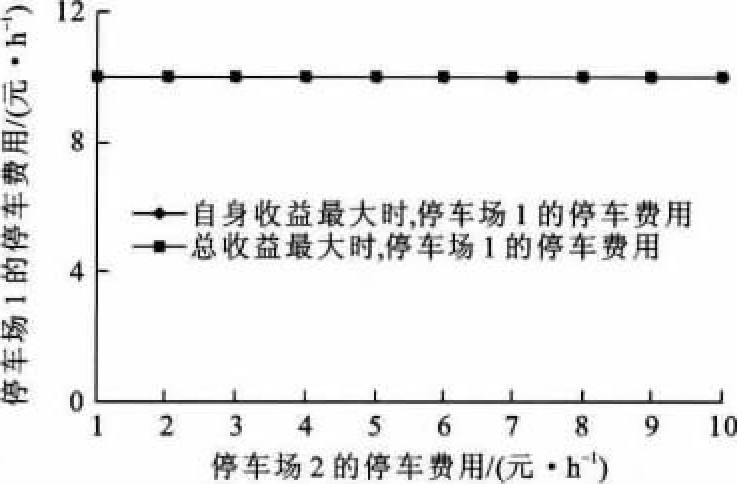
当停车场1的停车费用在1~10元·h-1时, 图 6、7分别为平峰时段和高峰时段停车场2随停车场1收费的变化而对应的最优收费。同样, 当停车场2的停车费用在1~10元·h-1时, 图 8、9分别为平峰时段和高峰时段停车场1随停车场2停车费用的变化而对应的最优收费。
从图 6~9可以看出, 在平峰时段, 随着停车场1停车费用的增加, 停车场2令其自身停车收益最大的停车费用呈上升趋势, 令总停车收益最大的停车费用先上升, 达到10元·h-1后保持不变, 反之亦然。这是因为在平峰时段, 随着停车费用的增加, 停车流量的转移相对于流量基数来说比较大, 影响明显。当一个停车场的停车费用较低时, 另一个停车场的费用增加到一个较小值时, 停车流量已大量转移, 使其停车收益开始降低, 当一个停车场的停车费用较高时, 另一个停车场的费用需增加到一个较大值时, 减少的停车流量才会使停车收益开始降低。而对于总停车收益, 当一个停车场的停车费用达到7元·h-1及以上时, 即使另一个停车场的停车收益开始降低, 两者之和仍继续上升, 始终在停车费用为10元·h-1时才达到最大收益。而在高峰时段, 尽管一个停车场停车费用的增加使其停车流量有所减小, 但由于停车流量基数很大, 因此, 停车收益仍不断上升。一个停车场的停车费用在1~10元·h-1时, 另一个停车场令其自身收益和总收益最大的停车费用均始终为10元·h-1。
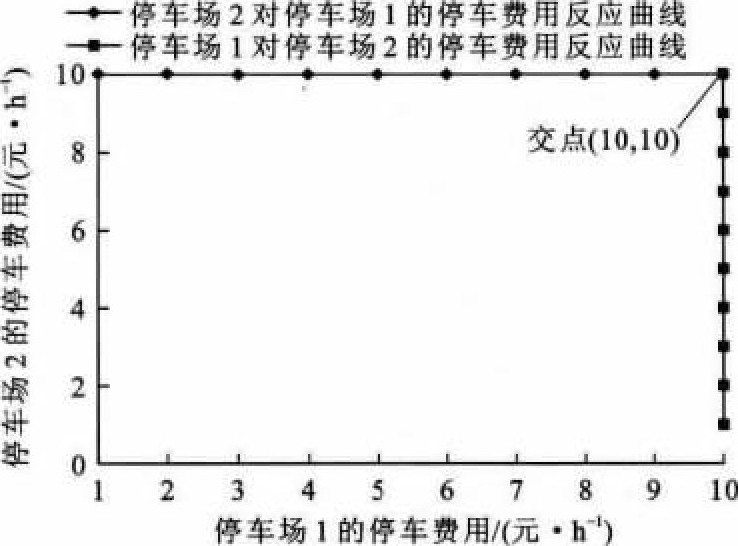
在上述算例中, 2个停车场之间存在博弈关系, 均根据另一个停车场的停车费用来制定自身的费用, 以达到自身停车收益最大。在停车场1的停车费用变化时, 停车场2令其自身停车收益最大的停车费用曲线即为停车场2对停车场1的停车费用反应曲线, 也是停车场2的最优决策曲线, 反之亦然。将2个停车场的停车费用反应曲线画到一个图上, 两者交于一点, 该点即纳什均衡点, 即最优决策点, 其对应的2个停车场的停车费用, 为最优决策停车费用。图 10、11分别给出了平峰时段和高峰时段的纳什均衡点。
从图 10、11可以看出, 在平峰时段, 2个停车场的最优决策费用均为5元·h-1。在高峰时段, 停车流量很大, 2个停车场之间的分配随停车费用变化而变化的影响不明显, 停车收益始终随着停车费用的增加而上升, 因此, 2个停车场的最优决策费用均为最高限价10元·h-1, 此时停车收益最大。
6. 结语
本文主要在理论上对城市停车收费优化模型进行了研究, 提出了一种新的研究方法和思路。在本文算例中, 简化了网络结构与停车设施分类, 并假定某一时段内的区域停车总需求固定不变, 即不会因为停车费用的变化而变化, 这与实际情况有所出入。另外, 停车费用变化范围也不能完全反映停车费用与停车收益的相互关系, 因此, 本文的结果与分析都存在着一定的局限性, 只是在一定程度和范围内给出了城市停车收费优化问题的理论依据。此外, 本文中所采用的算例为相关研究中的经典网络, 相关数据和参数的获取较容易, 然而, 算例太过简单, 只能说明所提模型及算法的有效性, 而无法论证本文的实用价值。由于可获取的城市交通数据过于粗略, 模型中的相关数据和参数无法通过这些数据进行估算, 而规模较小的城市又缺乏基础数据的采集制度, 因此, 在目前条件下, 很难通过实际数据分析和验证所提交通模型和方法。如果条件成熟, 采用实际数据对模型进行测算分析, 将具有更加重要的现实意义。
需要指出的是, 本文借鉴了收益管理的思想, 采用双层规划模型描述了城市停车收费的优化问题, 其目标是停车收益最大化。然而在实际中, 城市停车管理的目标不仅仅是收益最大化, 还包括降低道路拥挤与实现社会公平等目标, 因此, 如何更加全面地描述停车收费优化目标与如何更加科学地对动态停车流量分配进行建模是需要进一步研究的问题。参考文献:
-
表 1 路段参数
Table 1. Road section parameters

表 2 停车场参数
Table 2. Parameters of parking plots

表 3 不同路段的计算结果
Table 3. Calculation results for different road sections
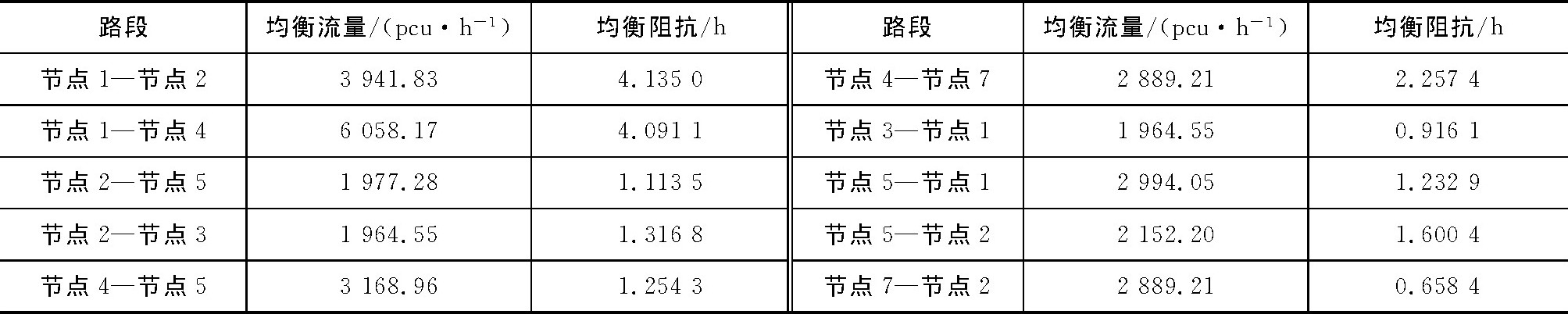
表 4 不同停车场的计算结果
Table 4. Calculation results for different parking plots
-
[1] 郭涛, 杨涛, 王瑞萍, 等. 城市停车设施规划的一种新决策方法[J]. 交通运输系统工程与信息, 2006, 6 (4): 95-99. doi: 10.3969/j.issn.1009-6744.2006.04.020GUO Tao, YANG Tao, WANG Rui-ping, et al. A new decision-making method of urban parking facilities[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6 (4): 95-99. (in Chinese). doi: 10.3969/j.issn.1009-6744.2006.04.020 [2] 石琼, 吴群琪. 拥挤收费为主导缓解城市交通拥挤可行性研究[J]. 长安大学学报: 社会科学版, 2004, 6 (3): 38-42. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200403010.htmSHI Qiong, WU Qun-qi. Feasibility research on congestion pricing for our urban traf fic congestion[J]. Journal of Chang'an University: Social Science Edition, 2004, 6 (3): 38-42. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XBJZ200403010.htm [3] 裴玉龙, 刘春晓. 停车换乘站位置选择及换乘需求预测[J]. 长安大学学报: 自然科学版, 2005, 25 (1): 60-64. doi: 10.3321/j.issn:1671-8879.2005.01.015PEI Yu-long, LIU Chun-xiao. Park-and-ride station location and its demand predicting[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25 (1): 60-64. (in Chinese). doi: 10.3321/j.issn:1671-8879.2005.01.015 [4] 钟慧玲, 徐建闽, 屠宇. 基于专用短程通信的停车引导和信息系统[J]. 长安大学学报: 自然科学版, 2004, 24 (2): 66-69. doi: 10.3321/j.issn:1671-8879.2004.02.016ZHONG Hui-ling, XU Jian-min, TU Yu. Parking guidance and information system (PGIS) based on dedicated short range communication (DSRC)[J]. Journal of Chang'an University: Natural Science Edition, 2004, 24 (2): 66-69. (in Chinese). doi: 10.3321/j.issn:1671-8879.2004.02.016 [5] 樊建强, 郝国瑞, 童夏. 城市道路拥堵收费的理论架构、实践效果及启示[J]. 长安大学学报: 社会科学版, 2013, 15 (4): 31-38. doi: 10.3969/j.issn.1671-6248.2013.04.006FAN Jian-qiang, HAO Guo-rui, TONG Xia. Urban road congestion charging theory, practice and enlightenment[J]. Journal of Chang'an University: Social Science Edition, 2013, 15 (4): 31-38. (in Chinese). doi: 10.3969/j.issn.1671-6248.2013.04.006 [6] GUR Y J, BEIMBORN E A. Analysis of parking in urban centers: equilibrium assignment approach[J]. Transportation Research Record, 1984 (957): 55-62. [7] PHANSAK S. Development of parking choice models for special events[R]. Madison: University of Wisconsin-Madison, 2002. [8] 严海, 杨晓光, 严宝杰. 特殊活动的停车选择模型研究[J]. 中国公路学报, 2005, 18 (2): 90-93. doi: 10.3321/j.issn:1001-7372.2005.02.018YAN Hai, YANG Xiao-guang, YAN Bao-jie. Parking choice model study for special event[J]. China Journal of Highway and Transport, 2005, 18 (2): 90-93. (in Chinese). doi: 10.3321/j.issn:1001-7372.2005.02.018 [9] 田琼, 黄海军, 杨海. 瓶颈处停车换乘logit随机均衡选择模型[J]. 管理科学学报, 2005, 8 (1): 1-6. doi: 10.3321/j.issn:1007-9807.2005.01.001TIAN Qiong, HUANG Hai-jun, YANG Hai. Mode choice models based on logit stochastic equilibrium in transportation systems with park-and-ride option[J]. Journal of Management Sciences in China, 2005, 8 (1): 1-6. (in Chinese). doi: 10.3321/j.issn:1007-9807.2005.01.001 [10] 李志纯, 朱道立. 能力约束下的停车行为模型及其求解算法[J]. 中国公路学报, 2007, 20 (5): 89-94. doi: 10.3321/j.issn:1001-7372.2007.05.016LI Zhi-chun, ZHU Dao-li. Model and its algorithm for modeling parking behavior with capacity constraints[J]. China Journal of Highway and Transport, 2007, 20 (5): 89-94. (in Chinese). doi: 10.3321/j.issn:1001-7372.2007.05.016 [11] 四兵锋, 张好智, 孙会君, 等. 能力约束条件下的城市道路及停车流量分配模型及算法[J]. 交通运输系统工程与信息, 2009, 9 (3): 78-85. doi: 10.3969/j.issn.1009-6744.2009.03.012SI Bing-feng, ZHANG Hao-zhi, SUN Hui-jun, et al. Urban road and parking assignment model and its algorithm with capacity constrain[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9 (3): 78-85. (in Chinese). doi: 10.3969/j.issn.1009-6744.2009.03.012 [12] BELOBABA P P. Airline yield management: an overview of seat inventory control[J]. Transportation Science, 1987, 21 (2): 63-73. doi: 10.1287/trsc.21.2.63 [13] GALLEGO G, RYZIN G V. Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J]. Management Science, 1994, 40 (11): 999-1020. [14] GALLEGO G, VAN RYZIN G G. A multiproduct dynamic pricing problem and its applications to network yield management[J]. Operation Research, 1997, 45 (1): 24-41. [15] FENG You-yi, GALLEGO G. Optimal stopping times for end of season sales and optimal stopping times for promotional fares[J]. Management Science, 1995, 41 (8): 941-956. [16] FENG You-yi, XIAO Bao-chun. Optimal policies of yield management with multiple predetermined prices[J]. Operations Research, 2000, 48 (3): 332-343. [17] ZHANG Dan, COOPER W L. Revenue management for parallel flights with customer-choice behavior[J]. Operation Research, 2005, 53 (3): 415-431. [18] 四兵锋, 孙壮志, 赵小梅. 基于随机用户平衡的混合交通网络流量分离模型[J]. 中国公路学报, 2006, 19 (1): 93-98. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601019.htmSI Bing-feng, SUN Zhuang-zhi, ZHAO Xiao-mei. Urban mixed network flow-split model and its algorithm based on stochastic user equilibrium[J]. China Journal of Highway and Transport, 2006, 19 (1): 93-98. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200601019.htm [19] 四兵锋, 赵小梅, 孙壮志. 城市混合交通网络系统优化模型及算法[J]. 中国公路学报, 2008, 21 (1): 77-82. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200801015.htmSI Bing-feng, ZHAO Xiao-mei, SUN Zhuang-zhi. System optimization model and its algorithm for urban mixed traffic network[J]. China Journal of Highway and Transport, 2008, 21 (1): 77-82. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200801015.htm [20] 四兵锋, 高自友, 林兴强. 停车诱导信息系统条件下的城市交通网络SUE配流模型及算法[J]. 公路交通科技, 2006, 23 (1): 120-124. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200601029.htmSI Bing-feng, GAO Zi-you, LAM W H K. Stochastic user equilibrium model for traffic assignment under parking guidance information system[J]. Journal of Highway and Transportation Research and Development, 2006, 23 (1): 120-124. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200601029.htm [21] 四兵锋, 林兴强. 交通信息条件下道路和停车选择SUE模型及算法[J]. 管理科学学报, 2007, 10 (2): 19-25. https://www.cnki.com.cn/Article/CJFDTOTAL-JCYJ200702003.htmSI Bing-feng, LAM W H K. Stochastic user equilibrium model for parking and route choice under advanced travel information system[J]. Journal of Management Science in China, 2007, 10 (2): 19-25. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JCYJ200702003.htm -






 下载:
下载:











 下载:
下载: