Phase-state identification of traffic flow in terminal area incorporated with prior experience clustering
-
摘要: 以终端区交通流为研究对象, 基于航迹谱聚类结果定义并提取交通流特征, 分析了特征间关系与交通流相态演化规律, 发掘了实测数据下交通流的自由态、平稳态与拥堵态, 以此为先验经验进一步设计因子分析与遗传期望最大化模糊聚类算法相结合的终端区交通流态势识别方法, 实现对交通流状态影响因素与交通流隐性特征的提取, 选取典型繁忙终端区的实测数据进行验证。分析结果表明: 基于客观数据挖掘的交通流态势识别方法具有良好的适应性与准确性, 自由态、平稳态与拥堵态的模型识别数量分别为6、36、37, 管制员判别数量分别为7、40、32, 误差率分别为14.3%、10.0%、15.6%, 模型识别率均在84%以上; 提取的交通流相态及时空特征可从局部细节构建终端区整体运行态势, 为终端区流量时空分布调配与进离场程序优化提供支撑。Abstract: The traffic flow in terminal area was taken as research object, and the characteristics of traffic flow were defined and extracted based on the result of trajectory spectral clustering.The relationship of characteristics and phase-state transition law of traffic flow were analyzed to reveal three phase-states of traffic flow under observed data, including free state, steady state and congestion state, which was regarded as prior experience to further design the identification method of traffic flow situation in terminal area combining factor analysis and fuzzy clustering algorithm of genetic expectation maximization, the influence factor of traffic flow state and the recessive characteristics of traffic flow were extracted, and the observed data from typical busy terminal area were chosen to do the verification.Analysis result shows that the identification method of traffic flow situation based on objective data mining has good adaptability and accuracy, the identification numbers by the method for free state, steady state and congestion state are 6, 36 and 37 respectively, the discrimination numbers by the controller are 7, 40 and 32 respectively, the error rates are 14.3%, 10.0% and 15.6% respectively, and the identification rates are all above 84%;the extracted phase-state and time-spatial characteristic of traffic flow can be used to structure the overall operation situation in terminal area from local detail, which can provide support for the time-spatial distribution allocation of flow in terminal area and theoptimization of arrival and departure procedure.
-
0. 引言
交通流状态的识别与分析在道路交通领域已经进行了较为深入的探索, 这些研究以交通流基本特征与相变原理为理论基础[1], 利用地面智能交通设备采集实际数据, 使用不同的统计分析与挖掘方法提取数据间的变化特征与关系[2], 实现交通状态及特殊事故的有效识别, 为空中交通的相关研究提供了有益的借鉴。
空中交通流特性研究起步较晚, 目前, 国内外研究基本集中于交通流建模与运行仿真层面, 侧重理论模型的构建及特点分析。Menon等采用欧拉方法建立了宏观的交通流模型以简化其特征描述[3]; Hu等通过交通流量与密度关系描述交通流状态并构建了相应的状态预测模型[4]; 王莉莉等研究了空中高速路交通流微观跟驰模型, 分析了航空器间隔、初始速度及流量间的影响关系[5]; Zhang等基于广义跟驰行为的建模与仿真试验研究了终端区交通流的相变问题[6-7]。由于运行环境与约束条件的不同, 空中交通与地面交通间存在固有差异, 对于空中交通流的基本特征发掘及相变关系研究尚不深入, 未形成较为统一的认知, 因此, 相应的交通态势判别与评估仍采用空管传统指标进行整体态势分析。李楠等以航班数、复杂度、容流比、高度层变化数量及速度等传统指标构成的特征向量, 并引入主观交通状态变量, 运用聚类方法对终端区交通态势进行判别[8-9]。另一方面, 对于空管实测数据的挖掘分析, 除航迹聚类与预测外, 大多以空域运行效率指标及流量策略实施数据为特征[10], 发掘不同交通场景下的空域运行特点, 识别影响空域系统效能的主要因素[11-13], 以帮助验证流量管理的有效性, 或者利用聚类分析局部空域中航空器聚集密度来刻画交通态势及拥塞程度[14-15]。
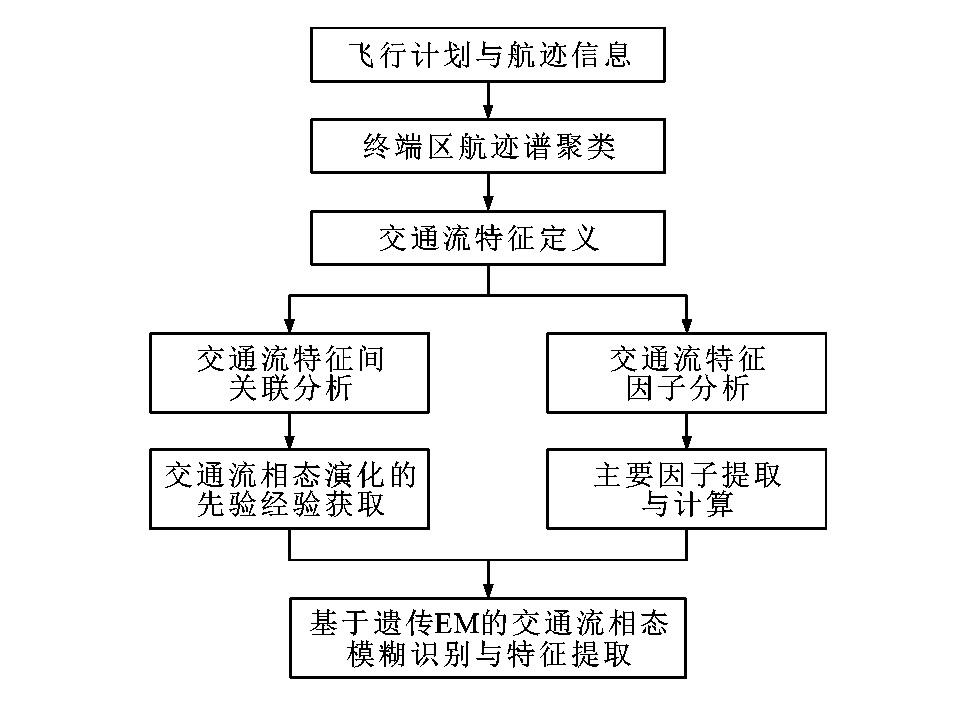
上述这些研究以建模仿真数据或传统量化指标为依据进行空域运行特征与态势分析, 缺乏实测的交通流时空特性与演化规律支撑, 并不能全面、客观地反映空域及交通流的实际运行状态, 对流量管理策略的准确实施难以形成有效辅助决策, 因此, 本文提出了一种融合先验经验聚类的交通流相态识别方法, 具体过程见图 1。该方法以终端区交通流相态为研究对象, 先依据实际采集的航班飞行计划与雷达航迹数据, 借助优化的航迹谱聚类方法进行进离场交通流的划分, 提取相应的航迹属性与交通流特征。以此为基础, 进一步分析各特征间的关系与变化规律, 发掘管制认知下的交通相态演化现象, 获取先验知识, 并通过因子分析提取表征交通流相态的主要因素, 消除特征间的相关性。之后, 采用遗传期望最大化(Expectation Maximization, EM)算法构建交通流相态的模糊聚类判别方法与模型, 抽象出终端区交通相态隐性特征向量。选取国内典型繁忙终端区, 分析了终端区进场交通态势时空分布特征, 验证了方法的有效性。提出的交通流特征指标与相态识别方法的目的是通过单个交通流相态的准确识别, 构建全面、客观的终端区整体运行态势表征与监控, 以支持战术预战术阶段的流量管理决策, 如终端区走廊口间的流量调配、临时航线使用等, 提升终端区运行效率。
1. 基于航迹的交通流特征定义
1.1 航迹数据处理与聚类
终端区航迹聚类可应用于交通流与进离场程序识别[16-17]、空域运行状态监视[18]。采用一种基于图论的航迹谱聚类方法, 可识别不同形态的样本空间, 避免样本导致的局部最优解情况[19], 其基本思想是依据航空器飞行轨迹构建相似性矩阵, 利用图的最优分割方法实现航迹划分及中心航迹提取。
航迹数据以终端区内机场基准点为中心, 按照半径为50kn、高度为5 000m以下的空间范围进行筛选, 剔除飞越航班与孤立的异常雷达数据, 确定原始航迹样本。单个航空器原始航迹由间隔为16s的多个雷达点序列构成。为适应谱聚类算法要求, 对原始样本重新采样。通过航迹的时间归一化, 将原始航迹样本转换至[0, 1]时间段上的航迹分布, 依据时间间隔进行航迹点线性插值计算, 将航迹表示为数量相同且时间分布一致的雷达点所构成的等长向量以满足相似度计算的条件。引入距离修正因子与航线修正因子, 采用基于欧式距离的度量方法所得相似度r为

式中: xk为不同航班对应点之间航迹k的等角距离; M为航迹总数; v为等角距离集合方差; h为航迹间的距离小于1kn且航线夹角小于10°状况的出现数量。
由此构建航迹间的相似度矩阵, 进一步获取规范化的亲和度矩阵及特征矩阵, 并实施无监督的聚类计算[20], 自行判别聚类划分数量。以广州白云机场终端区单日进场航迹数据为样本, 针对北向与南向两种运行模式分别进行聚类, 聚类结果见图 2。北向模式下包含7类划分, 南向模式下包含9类划分, 不同的航迹划分可较准确地识别各进场定位点所对应的进场航班流及进场程序。
1.2 航迹属性与交通流特征向量定义
由航班构成的交通流是空域运行的动态性主体, 对于空域运行态势的表现仅以宏观架次、容流比及延误水平进行度量并不完善。借助交通流的状态变化及其分布特征, 可发掘管制动态特征、交通流与空域的适应情况, 从管制负荷及运行效能层面表征详细的空域态势, 实施客观的评价与度量, 从而为流量调配决策提供数据依据。以此为考量, 可从聚类结果中提取相关特征。
以终端区不同运行模式下每个划分的聚类中心作为对应进场定位点的参考航迹或参考进场程序[20-21]。其聚类成员为遵循该程序运行的航空器轨迹向量, 构成实际的交通流。由于气象及军事活动影响, 参考航迹并不等同于标准程序, 仅依赖于雷达数据的时空特征可更客观地表征实际飞行特征与管制意图。单个航迹的基本属性包括航迹距离、航迹时长与高度下降率, 航迹距离为终端区内航迹雷达起始点至末点的实际飞行距离, 航迹时长为航迹自雷达起始点至末点间的飞行时间, 高度下降率为航迹起始点、末点间高度差值与航迹时间的比值, 表征航空器下降平均速率。
基于聚类结果及参考航迹, 进一步定义单条航迹的3个属性值, 相对飞行速度、航迹吻合度与前序等待落地航班数。相对飞行速度为标称飞行距离与航迹时长的比值, 标称飞行距离即聚类对应的参考航迹长度[22]。与地面交通不同, 终端区内航空器通过调速、雷达引导下的机动运行或空中等待实现间隔保持以及场面时隙的匹配。由于航空器速度不可能无限减小, 平均飞行速度只能一定程度上反映航空器的调速行为, 而相对飞行速度可同时实现对引导机动及空中等待行为的表述。航迹吻合度为航班的航迹与所属聚类的参考航迹间的差异性, 以航迹相似度进行度量。吻合度为0表示与参考航迹完全一致, 取值越大表示航迹间差异越明显。吻合度可体现交通流中航迹的规范程度及运行的有序性。当吻合度取值增大时, 空域及交通流复杂度上升, 管制员为保证运行安全与机场跑道资源的高利用率, 所投入的管制精力及负荷水平将明显增加。前序等待落地航班数为航班进入终端区至落地的时间范围内到达的航班架次。纳入统计的航班限定于与该航迹存在航段汇聚的航班流, 航班流以聚类划分结果为依据。由于终端区进场航班流最终必然呈现交汇状态, 因此, 采用通过汇聚点或公用航段的航班排队数可有效体现交通运行瓶颈态势。
基于上述单条航迹属性, 按照统计间隔进行属性均值与标准差计算, 定义某时间段内交通流特征向量e为

式中: D为平均航迹距离, 由所有航迹距离之和除以航迹数得出; T、H、C、V、W分别为平均航迹时长、平均下降率、平均吻合度、平均相对速度与平均等待队列, 计算公式与D相似; σ1、σ2、σ3、σ4、σ5分别为航迹距离标准差、航迹时长标准差、下降率标准差、吻合度标准差与相对速度标准差, 标准差指标用以表征交通流中航空器运行的可预测性与相似性。
由此构建的终端区交通流态势时空变化的特征向量, 其度量涵盖水平距离、高度剖面、时间、相似性及波动程度等维度。依据原始样本与聚类输出, 可获取聚类划分对应交通流的特征矩阵。
2. 终端区进场相态特征分析
针对已定义的交通流特征, 依据实测数据计算特征数值, 通过非线性拟合的方法分析不同特征量之间的变化关系, 发掘典型的交通流相态演化规律, 提取相态划分的先验知识。本文采用广州白云机场终端区2014年3月的实测数据, 以北向模式定位点GYA进场航班流为例。
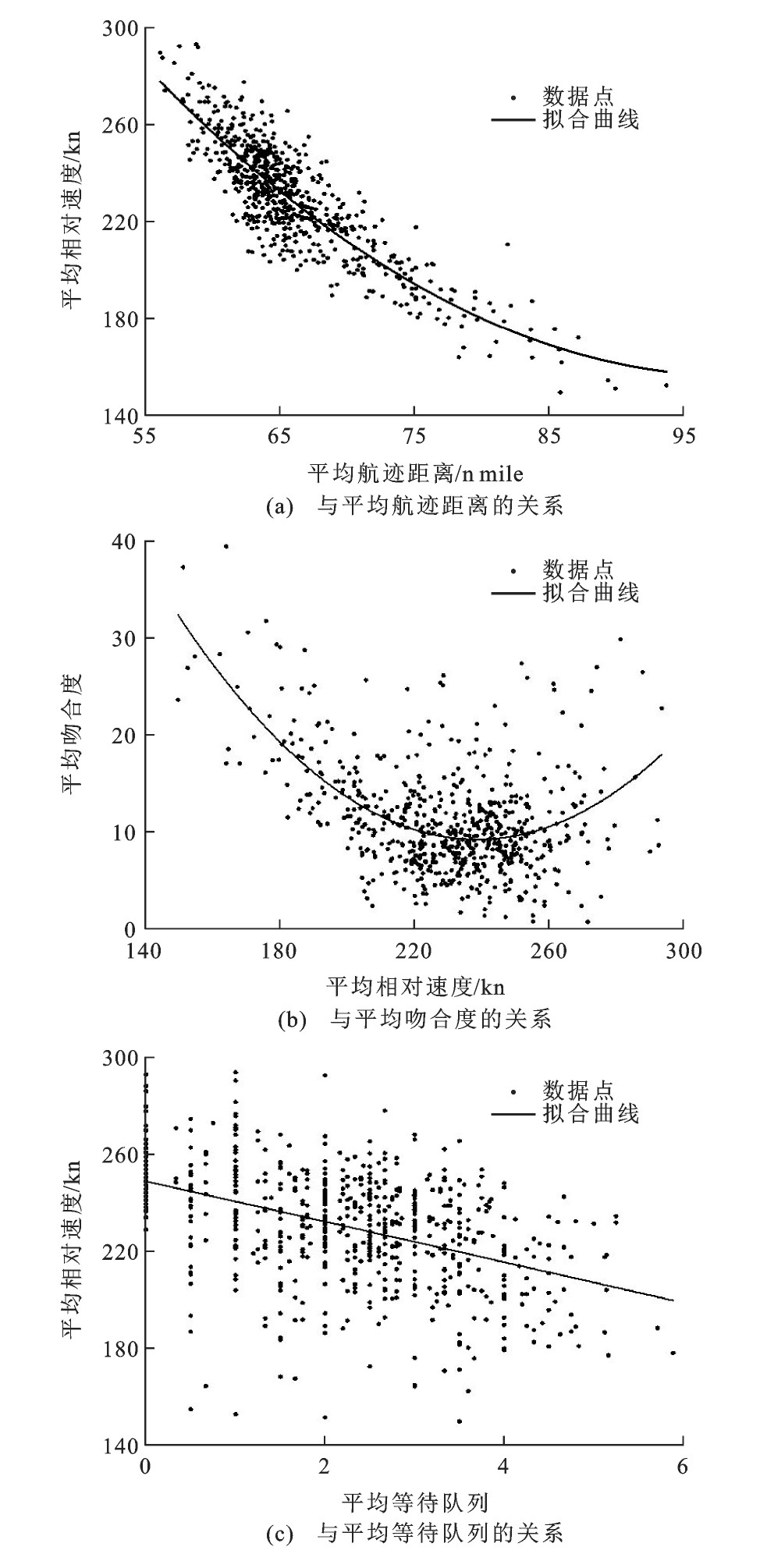
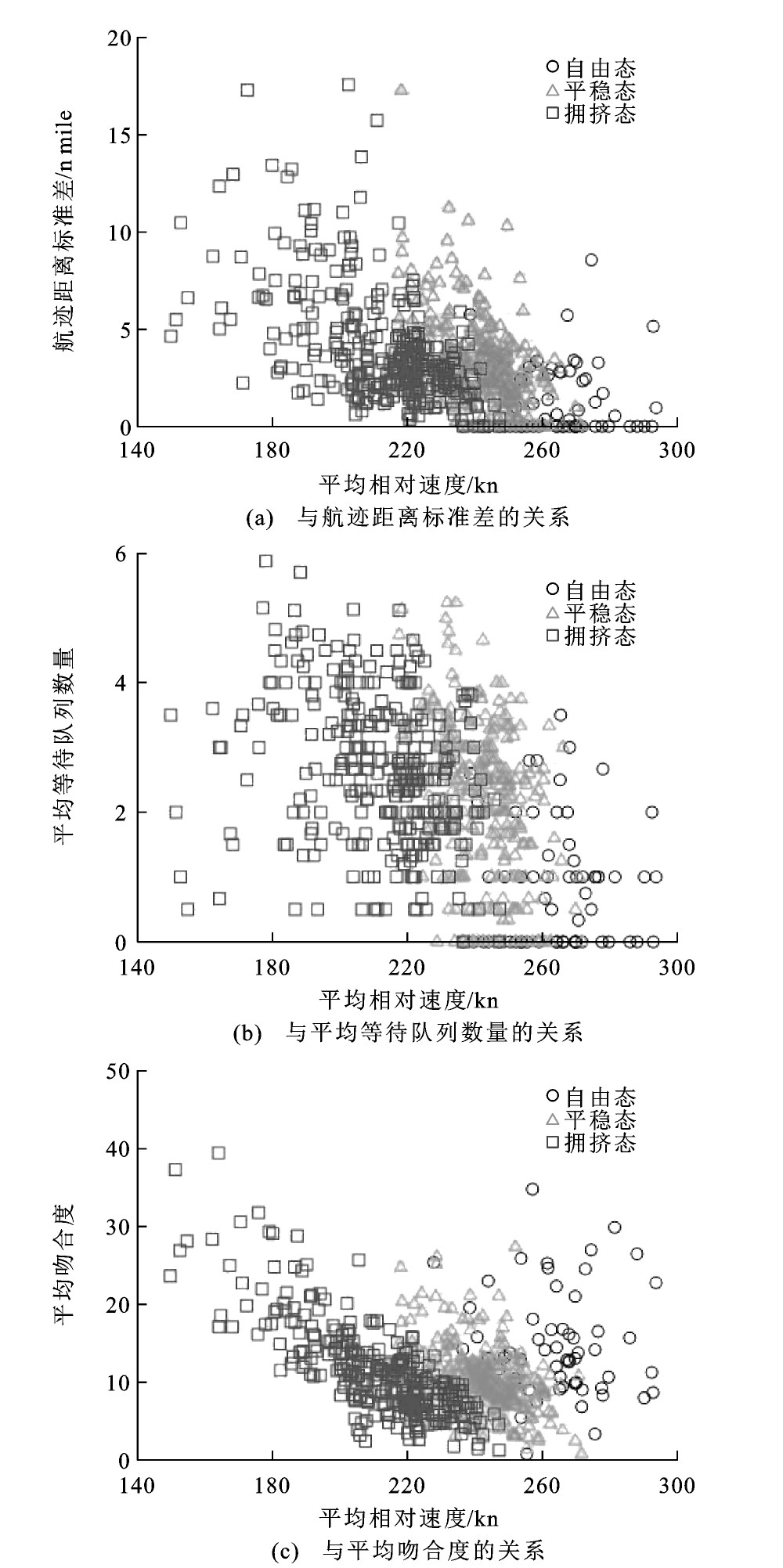
首先, 选取平均相对速度进行分析, 平均相对速度与平均航迹距离、平均吻合度、平均等待队列的关系见图 3。当平均相对速度快速下降时, 平均航迹距离起初呈现相对缓慢增长, 之后逐渐加速并转变为快速递增; 平均吻合度的趋势变化更为显著, 当平均相对速度减小, 吻合度数值逐步减小, 呈现相对稳定的汇聚状态, 之后, 平均相对速度进一步降低, 吻合度反转而快速升高, 形成明显的相态转换; 随着平均等待队列数的不断增加, 平均相对速度则表现为整体下降趋势。
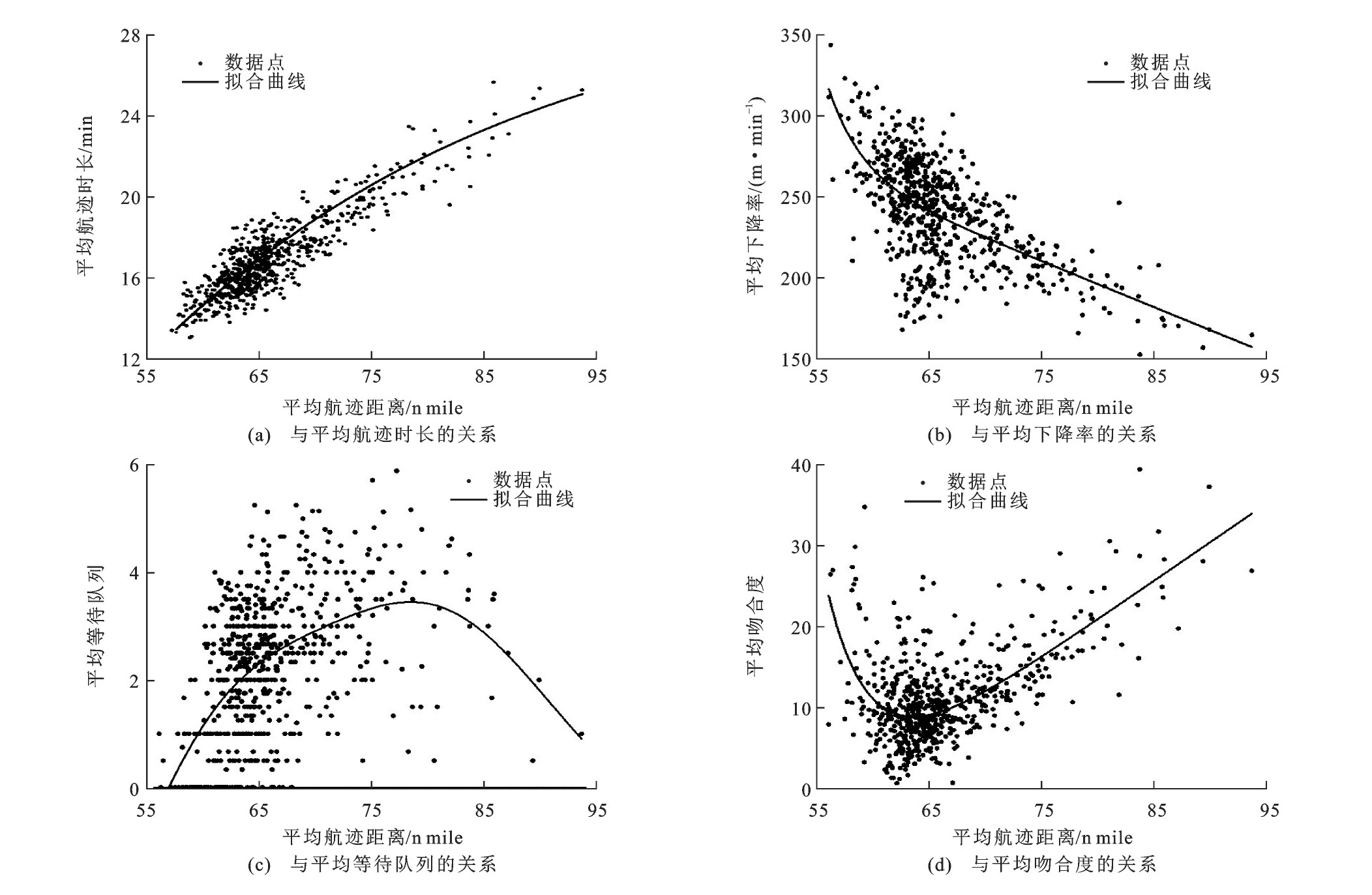
之后, 选取较为直观的平均航迹距离进行分析, 平均航迹距离与其他均值的关系见图 4。当平均航迹距离处于较低水平时, 平均航迹时长相对于平均航迹距离呈现更快速的增长, 而后逐步转变为同步递增。平均下降率处于快速减小的阶段时, 平均航迹距离仅小幅增加, 而航空器平均等待队列数则上升明显, 表明此时更多采用调速控制间隔, 相应的航迹时长显著增加。随着平均航迹距离继续增加, 平均下降率变化逐渐变缓并维持在低位, 而平均等待队列数增长趋势同样减弱并表现出一定程度的回落。平均吻合度随着平均航迹长度持续增加表现为快速回落再反向持续上升。在特殊情况下, 终端区通行能力下降, 一般调速与雷达引导已无法满足航班运行安全要求, 需实施空中等待或大范围绕飞机动, 此时各特征量间的数值分布区域会产生较大偏移, 图 4各分图中的右侧散点, 对应2014年3月12日至13日终端区进场高峰时段存在明显气象影响的运行场景。
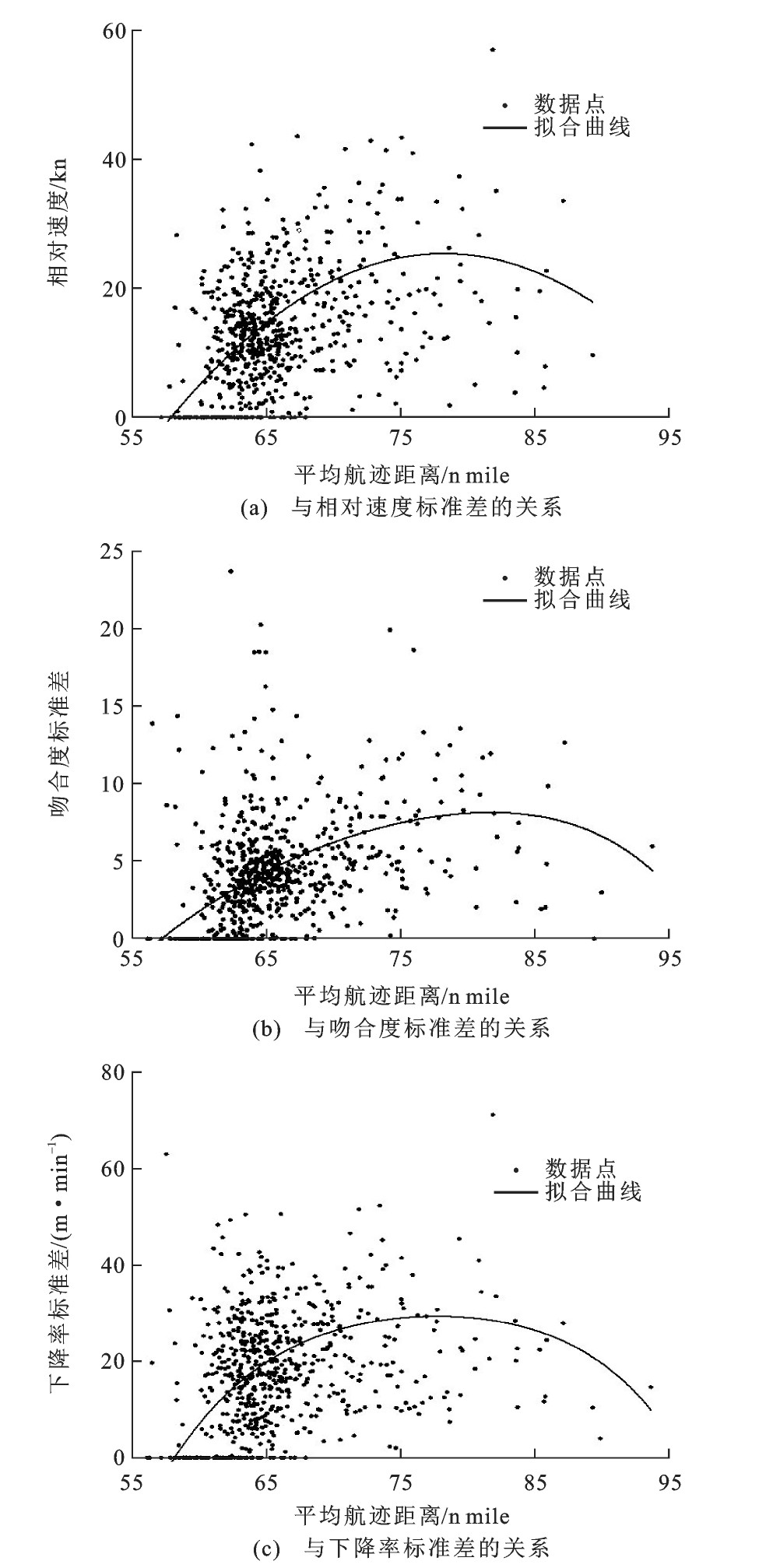
为考量交通流整体状态与航空器个体运行特征间的关系, 以平均航迹距离与标准差特征进行比较, 平均航迹距离与各标准差的关系见图 5。当仅有单架航空器时航空器相对自由, 可选择合适路径实施进场, 其航迹距离呈现在横轴上的散落分布。当交通流中存在多个航班, 个体间影响及运行差异逐渐呈现, 各标准差指标明显上升, 而平均航迹距离变化幅度较小, 表明此时实施以调速为主的管制干预。随着标准差所表征个体运行差异的进一步加剧, 航迹距离增速加快, 说明管制中采用了更多的雷达引导。标准差特征的数值回落则是由于在特殊条件下采取等待或机动措施, 尽管航迹产生了较大偏离, 但航班整体运行特征再次趋同。
最后, 分析各标准差特征间的分布, 可发现类似的交通流相态与管制偏好, 各标准差之间的关系见图 6。吻合度标准差相较于航迹距离标准差表现出先快后慢的增长速率变化, 而相对于航迹时长标准差则体现为相反的趋势, 表明交通流经历由无干预到调速干预, 再逐步转变为大量机动引导的策略变化。相对速度标准差与航迹距离标准差间的这种趋势变化表现更为明显。
基于各特征量之间变化关系所表现的运行特征一致性, 对交通流相态形成较为良好的表述与解释。参考地面交通中基于交通流基本参数的状态判别, 上述特征之间的分布关系可作为空中交通流状态变化的显性表征, 由此将终端区交通流较为直观地划分为3类相态, 即自由态、平稳态与拥堵态。自由态基本特征为航班流相对速度快、航迹距离短、航班实现连续下降以及航迹吻合度低, 其原因是交通密度较低, 航空器间基本无冲突, 管制员可选择最合适程序实施进场, 无须完全遵循标准程序, 相应管制负荷较低。平稳态特征表现为相对速度与下降率的显著降低, 航迹时长明显增加而航迹距离变化小, 航迹呈现极高的吻合度。此状态下排队数量持续增加并维持在较高水平, 交通流内部逐渐产生相互影响与制约, 管制员更倾向于按照标准程序实施进近, 并以调速为主要手段来保持间隔, 因此, 交通流整体相对速度下降, 航空器间形成明显的跟随行为, 航迹簇呈现高聚集性。航班个体间运行差异不大, 主要体现在速度与下降率的差别。拥堵态以较低的航迹吻合度及快速增加的航迹距离为主要特征。交通流整体相对速度与下降率进一步降低并保持低位。拥堵态下航空器相互制约进一步增强, 仅采用调速的管制干预方式难以持续, 为保证安全和时隙资源利用率, 管制员倾向使用更多的雷达引导机动。宏观上航迹束由汇聚逐渐转为发散状态, 微观上航空器运行差异快速分化, 部分航迹明显延长, 形成调速与航迹偏离的混合多发现象, 高度剖面则表现为长距离平飞与多阶段分步下降。空域交通复杂性加剧, 造成管制负荷迅速提升。随着交通量再次增加, 机动引导波及范围持续扩大, 航空器运行特征再次趋同, 标准差特征数值有小幅下降, 此时空域通行能力基本处于饱和, 无法容纳更多的航班。
针对各相态特征, 以2014年3月14日广州白云机场终端区航迹数据为例, 显示不同相态下交通流特征的差异, 交通流典型相态下航迹的水平与垂直分布见图 7。航迹在水平维度上呈现由离散至汇聚再转为大范围发散的变化。高度剖面方面, 以调速为主的平稳态下部分航空器呈现较为一致的高度改变方式, 航迹距离由自由态的60 n mile水平扩展为65 n mile左右, 拥堵态下航空器下降趋势表现为相互交错的分阶段下降, 个体差异性显著, 航迹距离进一步扩大为70~80 n mile。
3. 交通流特征因子分析
尽管显性特征可较好体现交通流的状态变化, 但各指标数值间相关性及固有的信息冗余将对相态评估与识别的效果产生影响, 尤其在基于模糊聚类分析的状态识别中, 输入数据无法满足相对独立的要求, 因此, 采用因子分析实现原始数据的降维处理, 通过多重共线性的消除将相似特征转化为相互独立的因子, 并依据其贡献程度保留核心特征的主要信息。
对特征向量中的各分量, 依据其相关性矩阵及主成分法提取主要因子。主要因子特征值应大于1, 累计贡献率超过80%, 显著性水平小于0.05且KMO统计量大于0.7[23-24]。同样以北向运行模式GYA的典型繁忙进场航班流实测数据为例进行因子提取, GYA交通流特征的因子分析结果见表 1, F1、F2、F3分别为密度调整因子、相似性因子、航迹吻合因子。
通过降维处理, 共提取3个主要因子, 累计贡献率超过81%, 各航迹特征具备较高共同度, 表明分析结果良好。依据贡献率排序, 将主要因子分别定义为密度调整因子、相似性因子、航迹吻合因子。密度调整因子数值显示, 平均航迹距离、航迹时长、下降率及相对飞行速度表现出较大的载荷, 表明该航班流的进场程序结构是影响其相态及通行能力的重要因素。无论调速或引导机动, 其目的都是通过管制干预使航迹距离或时长增加与下降率降低, 从而使进场航线在维持高承载能力的同时, 控制交通流局部时空密度, 从而确保汇聚点、公共进近航段或跑道等瓶颈部分的间隔安全与整体资源利用率。相似性因子与各主要标准差特征与平均等待队列关联明显, 体现构成交通流航班个体运行的有序性及运行可预测性对态势的影响, 而运行瓶颈所导致的等待队列是造成航空器运行特征分化的重要原因。航迹吻合因子含义最为明显, 它仅与航迹吻合度相关指标表现出高关联度, 吻合度作为航迹聚类的直观特征具有较好的判别意义, 体现当前时刻的管制偏好与航班整体运行特征。
表 1 交通流特征的因子分析Table 1. Factor analysis for traffic flow characteristic
4. 进场交通流相态提取方法
以提取的主要因子代替原有特征向量, 描述终端区交通流特征及相态变化。依据因子分析所得得分系数矩阵与样本数据, 计算各因子数值并分析其概率密度, 特征因子的概率分布见图 8。概率分布表现为混合高斯特征, 而不同相态下的交通流参数与航迹特征也符合高斯分布。基于此, 采用EM聚类对终端区交通流相态进行划分与识别[23]。
EM算法是解决缺值问题的传统方法, 其基本思想是依据当前参数对隐藏变量的期望值进行估计, 再计算混合分布的待估参数使其期望最大化, 并获取对数似然, 通过这2步的交替迭代使过程不断收敛。与K-means聚类不同, EM聚类不将某个实例明确归入某个划分, 而是提供其隶属与不同分布的概率, 是一种基于原型训练的模糊聚类方法, 适用于终端区交通流相态识别这类边界模糊的不确定性问题。虽然EM算法可利用对数似然函数作为聚类效果的评判, 实现无干预的类别划分, 但划分数量的搜索过程会导致算法效率的急速下降, 特别是对于高维向量的处理, 还可能引起局部最优问题的出现, 造成聚类含义的解释困难, 因此, 使用主要因子代替原有特征向量, 降低聚类对象维度, 并对聚类算法输入及收敛判别分别引入先验经验与适应度函数。具体步骤为: 依据交通特征的相变分析结果将聚类数量设置为3类, 即对应交通流自由态、平稳态及拥挤态, 采用K-means快速聚类进行效果初步验证, 并据此设置各混合分布的概率、向量均值等初始参数, 从而快速降低EM算法的时间复杂度; 在EM中引入遗传算法以实现全局最优[25], 采用改进的对数似然函数, 基于给定的阀值判别适应性的提高水平, 从而决定迭代的终止。改进的对数似然函数L(E|Θ)为

式中: E为交通流特征矩阵; Θ为EM算法输出的混合模型参数向量; αj为混合模型中第j个分布的权重; J为分布总数; ei为第i个统计时间段的交通流特征向量; I为统计时间段总数; θj为混合模型中第j个分布参数; gj(ei|θj)为第i个统计时间段内混合模型中第j个分布的密度函数。
依据最终的划分结果及输出的混合模型, 可提取终端区单个交通流相态隐性特征S=(S1, S2, S3)且S1+S2+S3=1, S1、S2、S3分别为自由态、平稳态、拥挤态对应的特征分量。若交通流整体负荷较轻, 表征自由态的特征分量S1呈现较高数值; 若交通流呈现多发拥堵, 则特征分量S3明显增加。由此, 隐性特征可直观表征交通流宏观运行状态。同时, 基于大样本训练获取的混合分布模型可依据实时航迹特征数据计算结果提供交通流相态动态判别。
5. 实例分析
5.1 交通流整体相态的隐性特征提取与分析
基于2014年3月广州白云机场终端区航班动态数据, 进行异常数据筛选, 按南向、北向运行模式分别实施航迹聚类, 计算各进场交通流基本特征矩阵, 并进行标准化处理。采用因子分析与遗传EM聚类结合的方法抽取各进场交通流相态隐性特征。其中, 定位点GYA、ATAGA、IGONO进场流为繁忙进场流, 流量在有效运行时间内基本维持在较高水平, P270与IDUMA整体流量水平较低。提取的交通流相态隐性特征见表 2。
依据提取特征可发现, 在北向运行模式下, GYA进场航班流呈现较明显的拥挤状态, 其概率与平稳态相当, 在有效运行时间内基本处于繁忙或拥堵状态, 管制干预程度较强。原因是GYA进场飞行距离短, 流量大, 并且落地不同跑道的航班存在较长的公共进近航段, 造成安全间隔上的控制困难; ATAGA与IGONO的流量与GYA相当, 但其进场程序飞行距离较长, 具备更大的调配余度, 表现为较好的航迹聚集程度, 交通流相态主要呈现平稳态; P270与IDUMA的流量相对较低, 呈现高比例的自由态与平稳态, 但由于进场距离偏短并与IGONO等航班流形成五边汇聚, 仍然存在少量拥挤状态。在南向运行模式下, GYA航班流相态分布发生较明显的变化, 拥挤程度大幅下降, 呈现高平稳态, 航迹规范性明显增强, 交通运行状态良好, 资源利用较高; 对于ATAGA与IGONO, 尽管其进场程序飞行距离显著减小, 但对应不同跑道划设了完全分离的进场路径, 无公共进近航段且航班量分布相对均匀, 可降低单股交通流密度, 并提供了空间上的调配余度, 因此, 飞经两点的交通流整体运行状态变化不大, 平稳态与拥挤态比率略有上升; P270与IDUMA则由于进场距离的增加, 交通流相态进一步向自由态偏移。
表 2 进场交通流相态隐性特征Table 2. Recessive characteristics of phase-states for inbound traffic flow
5.2 特征量与相态关联分析
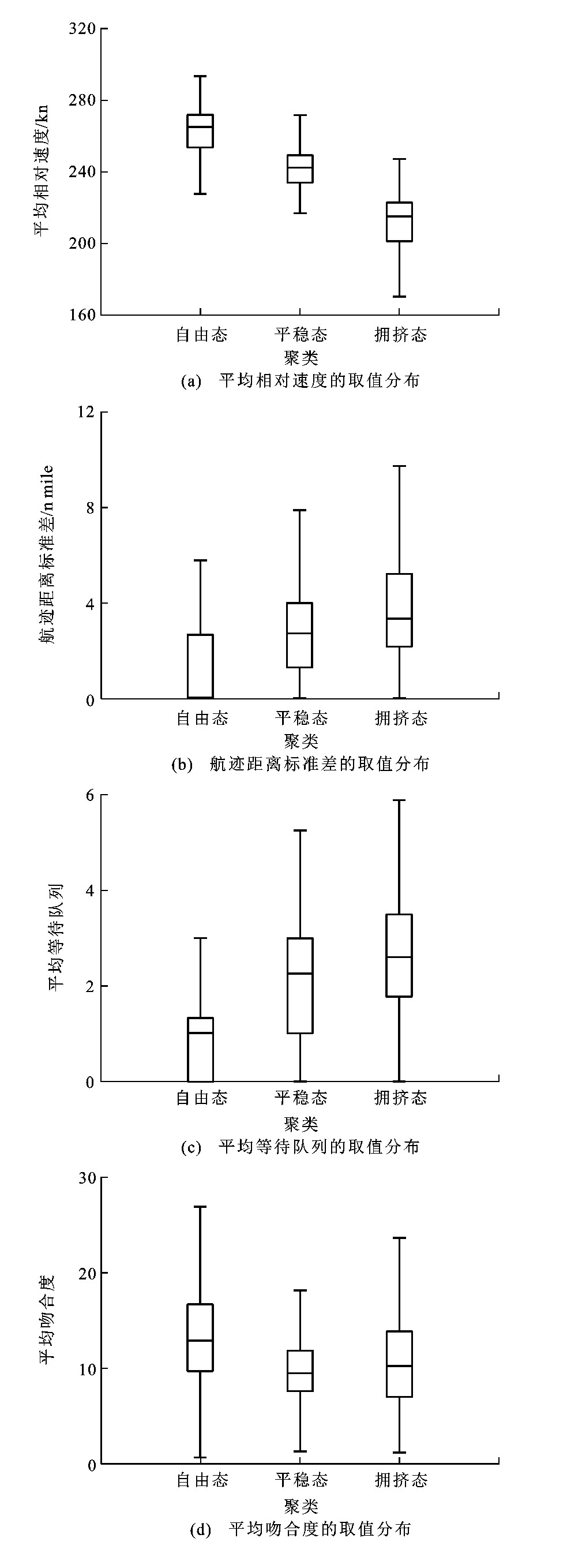
为验证原始航迹特征向量与交通流相态识别的关联性, 对不同聚类中特征分量的数值分布进行分析, 以北向模式下GYA航班流为例选取各主要因子中载荷较大的特征分量, 平均相对速度与其他特征分量的关系见图 9, 特征分量在不同聚类中的取值分布箱形图见图 10。各特征分量的数值间形成明显的划分聚集关系, 特征数值与聚类间具有显著关联, 其分布符合交通流相态演化的特征要素, 对交通流相态形成良好的判别度。其中, 平均相对速度具有最高的区分度, 不同聚类间仅存在小范围数值重叠, 表明密度调整因子提供的贡献度较高。航迹距离标准差与平均等待队列数量随相态迁移呈现数值上的增加, 在分布的高密度区间形成相对明显的差异。平均吻合度的聚类间分布差异性稍小, 原因是进场程序对航班运行的固定性约束, 使得平均吻合度不会表现为巨幅变化。同时, 在自由态与拥挤态下, 吻合度具备相似的高数值分布特征, 但表征了两类相态下不同的管制特征, 即自由选择路径与强管制干预。吻合度在配合密度调整因子的相关特征分量时, 可形成更显著的相态区分。
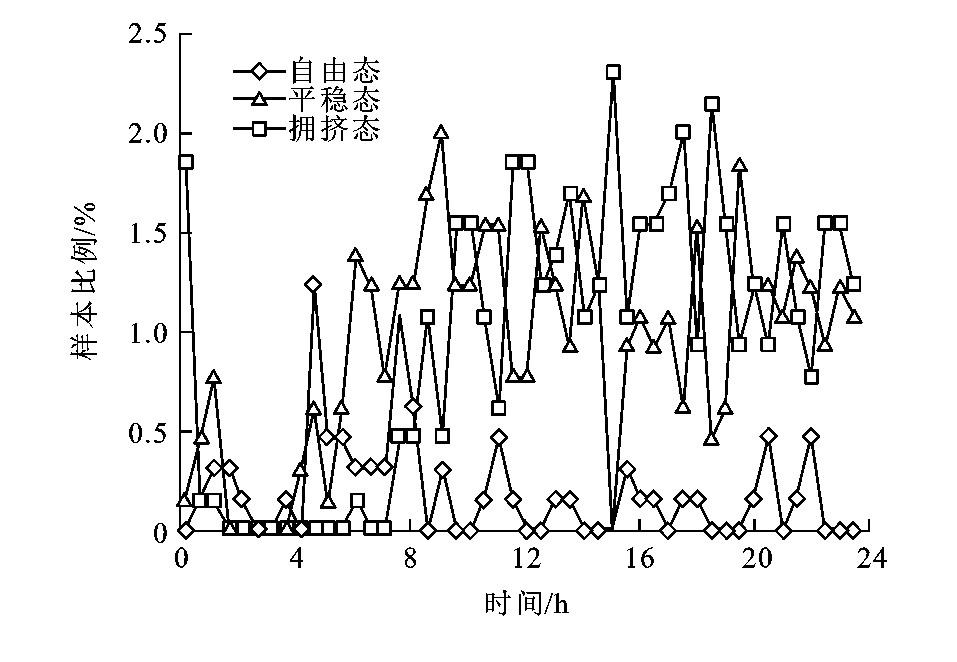
为验证交通态势的时空特征, 继续将样本数据与统计时间段关联, 每个时间段为30min, 各时间段中不同聚类样本的比例见图 11。在凌晨及7:30~8:30, GYA进场流中自由态呈现较高比例, 11:30~12:30、14:30~19:00以及22:30以后, 拥挤态呈现较高比例, 其余时段交通流以平稳态为主要特征。相态时空分布同样符合广州白云机场终端区日常运行特征, 其中高概率拥挤态时间的区间与白云机场进港高峰时段基本一致, 由此可知依据实测航迹特征的知识发掘结果符合交通流相态的特征要素, 其特性与相态的分布与实际交通流对象的相态变化规律相吻合。
5.3 交通流相态识别模型效果验证
基于样本学习获取的混合分布模型是遗传EM聚类的核心产物之一, 借助模型具备的缺值分析能力与实测航迹数据动态判别交通流在指定时间内的相态概率, 并按照最大隶属度原则将交通流归入高概率的相态。以2014年3月22日至23日GYA进场航班流为测试样本, 选取30min为观测时间段进行交通流相态识别。同时, 采集管制员对相态的主观评判进行比对, 对比结果见表 3。可知, 混合模型具有较高的判别精度, 识别率均在84%以上。判别出现偏差的样本基本处于相态迁移的交叠部分, 符合交通流相态及EM聚类本身具备的模糊性。
表 3 交通流相态识别对比结果Table 3. Comparison result of traffic flow phase-state identification
依据验证结果可知, 所构建的终端区交通流态势识别方法效果良好, 提取的隐性特征所反映的交通流整体态势与时空分布特征, 可作为战术预战术阶段的流量管理、进离场航线设计与优化的决策支持, 及辅助临时航线使用方案与实施条件的制定; 输出的混合概率模型所具备的交通流相态判别能力, 可实现战术阶段的终端区运行态势辅助监控, 提供管制运行负荷与效率的实施评测参考。相较于传统的、以终端区整体为对象的评判方法, 针对终端区不同走廊口进离场交通流的相态分析, 可表征终端区内部交通流的差异性特征, 构建更加客观、完备、细节化的终端区态势描述, 从而支持终端区不同方向流量比例与时空调配的决策, 适应实际管制运行的需求, 提升终端区运行效率。
6. 结语
(1) 本文依据无干预的航迹谱聚类结果提取终端区交通流特征矩阵, 基于特征间关联关系与变化规律进行交通流相态的演化分析, 讨论了不同相态下的航迹特性与管制干预偏好, 并以此作为先验经验, 采用因子分析法与遗传EM算法相结合的模糊聚类方法, 挖掘表征交通流相态的隐性特征并训练基于混合分布的相态识别模型。
(2) 以广州白云机场终端区为实例, 针对不同运行模式下进场航班流的实测数据进行了分析与验证, 其聚类结果及时空分布状态符合实际运行状况与管制认知, 具有良好的态势识别效果, 可作为实施不同阶段流量管理策略、优化进离场航线设计的重要依据, 有助于平衡终端区运行效率与管制负荷, 具有良好的理论与实践指导价值。
(3) 在本文基础上, 可进一步融合先验经验分析交通流特征的客观权重, 并结合部分宏观特征, 进一步优化交通流态势识别方法的适应性与准确性; 同时, 可发掘终端区内部交通流间的相互影响与内在机理, 尝试模式识别与模糊分类规则的提取, 以提供对交通流时空调配的理论与实践方法支撑。
-
表 1 交通流特征的因子分析
Table 1. Factor analysis for traffic flow characteristic
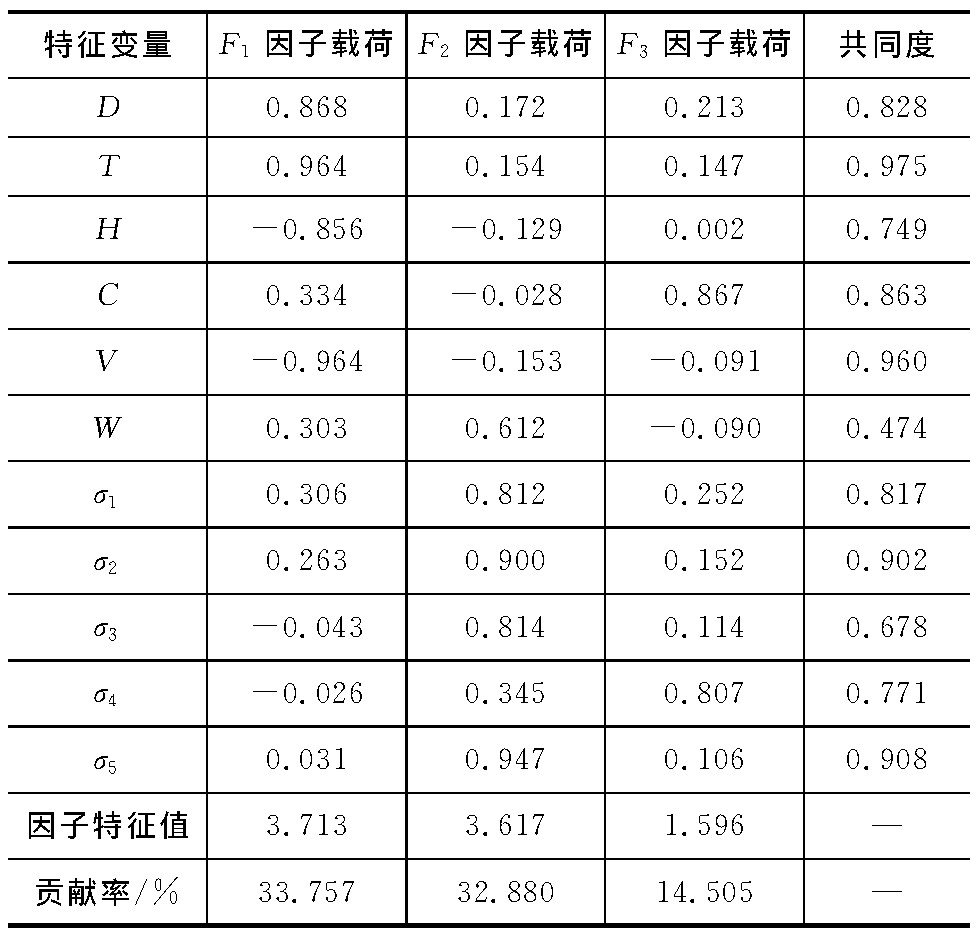
表 2 进场交通流相态隐性特征
Table 2. Recessive characteristics of phase-states for inbound traffic flow
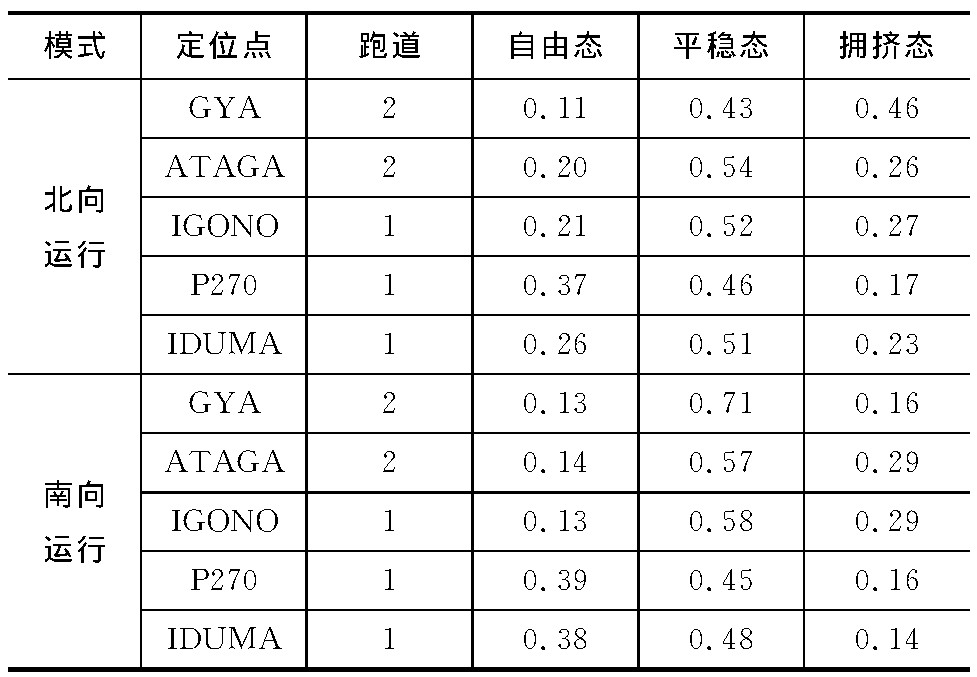
表 3 交通流相态识别对比结果
Table 3. Comparison result of traffic flow phase-state identification

-
[1] 陈德望. 基于模糊聚类的快速路交通流状况分类[J]. 交通运输系统工程与信息, 2005, 5(1): 62-67. doi: 10.3969/j.issn.1009-6744.2005.01.012CHEN De-wang. Classification of traffic flow situation of urban freeways based on fuzzy clustering[J]. Journal of Transportation Systems Engineering and Information Technology, 2005, 5(1): 62-67. (in Chinese). doi: 10.3969/j.issn.1009-6744.2005.01.012 [2] 徐琳, 曲仕茹. 基于数据流挖掘的交通流状态辨识方法研究[J]. 西北工业大学学报, 2011, 29(1): 34-38. doi: 10.3969/j.issn.1000-2758.2011.01.007XU Lin, QU Shi-ru. An effective RTRC-TFD method for detecting traffic flow using data stream mining[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 34-38. (in Chinese). doi: 10.3969/j.issn.1000-2758.2011.01.007 [3] MENON P K, TANDALE M D, KIM J, et al. A framework for stochastic air traffic flow modeling and analysis[C]//AIAA. 2010 AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2010: 1-28. [4] HU Jun, WU Zhen-ya. Research on the net amount of air traffic network[C]//SPIE. 2012International Conference on Graphic and Image Processing. Bellingham: SPIE, 2013: 1-7. [5] 王莉莉, 张新瑜, 张兆宁. 空中高速路交通流的跟驰现象及流量模型[J]. 西南交通大学学报, 2012, 47(1): 158-162. doi: 10.3969/j.issn.0258-2724.2012.01.026WANG Li-li, ZHANG Xin-yu, ZHANG Zhao-ning. Following phenomenon and air freeway flow model[J]. Journal of Southwest Jiaotong University, 2012, 47(1): 158-162. (in Chinese). doi: 10.3969/j.issn.0258-2724.2012.01.026 [6] ZHANG Hong-hai, XU Yan, YANG Lei, et al. Macroscopic model and simulation analysis of air traffic flow in airport terminal area[J]. Discrete Dynamics in Nature and Society, 2014, 2014: 1-15. [7] 张洪海, 杨磊, 别翌荟, 等. 终端区进场交通流广义跟驰行为与复杂相变研究[J]. 航空学报, 2015, 36(3): 949-961. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201503029.htmZHANG Hong-hai, YANG Lei, BIE Yi-hui, et al. Research on generalized following behavior and complex phase-transition law of approaching traffic flow in terminal airspace[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 949-961. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201503029.htm [8] 李楠, 任杰, 徐肖豪. 终端区交通态势识别研究[J]. 科学技术与工程, 2014, 14(11): 256-261. doi: 10.3969/j.issn.1671-1815.2014.11.056LI Nan, REN Jie, XU Xiao-hao. Identification of terminal area traffic situation[J]. Science Technology and Engineering, 2014, 14(11): 256-261. (in Chinese). doi: 10.3969/j.issn.1671-1815.2014.11.056 [9] 徐肖豪, 任杰, 李楠. 基于FCM的终端区交通态势识别[J]. 航空计算技术, 2014, 44(1): 1-4, 8. doi: 10.3969/j.issn.1671-654X.2014.01.001XU Xiao-hao, REN Jie, LI Nan. Identification of terminal area traffic situation based on FCM[J]. Aeronautical Computing Technique, 2014, 44(1): 1-4, 8. (in Chinese). doi: 10.3969/j.issn.1671-654X.2014.01.001 [10] REYNOLDS T G. Air traffic management performance assessment using flight inefficiency metrics[J]. Transport Policy, 2014, 34: 63-74. doi: 10.1016/j.tranpol.2014.02.019 [11] HOFFMAN B, KROZEL J, PENNY S, et al. A cluster analysis to classify days in the national airspace system[C]//AIAA. 2003AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2003: 1-12. [12] CHATTERJI G B, MUSAFFAR B. Characterization of days based on analysis of national airspace system performance metrics[C]//AIAA. 2007 AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2007: 1-15. [13] MUKHERJEE A, GRABBE S, SRIDHAR B. Classification of days using weather impacted traffic in the national airspace system[C]//AIAA. 2013Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2013: 1-11. [14] BILIMORIA K D, LEE H Q. Analysis of aircraft clusters to measure sector-independent airspace congestion[C]//AIAA. AIAA 5th Aviation, Technology, Integration, and Operations Conference. Reston: AIAA, 2005: 1-9. [15] BILIMORIA K D, JASTRZEBSKI M. Properties of aircraft cluster in the national airspace system[C]//AIAA. AIAA6th Aviation Technology, Integration, and Operations Conference. Reston: AIAA, 2006: 1-8. [16] 王超, 徐肖豪, 王飞. 基于航迹聚类的终端区进场程序管制适用性分析[J]. 南京航空航天大学学报, 2013, 45(1): 130-139. doi: 10.3969/j.issn.1005-2615.2013.01.022WANG Chao, XU Xiao-hao, WANG Fei. ATC serviceability analysis of terminal arrival procedures using trajectory clustering[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(1): 130-139. (in Chinese). doi: 10.3969/j.issn.1005-2615.2013.01.022 [17] 王超, 韩邦村, 王飞. 基于轨迹谱聚类的终端区盛行交通流识别方法[J]. 西南交通大学学报, 2014, 49(3): 546-552. doi: 10.3969/j.issn.0258-2724.2014.03.027WANG Chao, HAN Bang-cun, WANG Fei. Identification of prevalent air traffic flow in terminal airspace based on trajectory spectral clustering[J]. Journal of Southwest Jiaotong University, 2014, 49(3): 546-552. (in Chinese). doi: 10.3969/j.issn.0258-2724.2014.03.027 [18] GARIEL M, SRIVASTAVA A N, FERON E. Trajectory clustering and an application to airspace monitoring[J]. IEEETransactions on Intelligent Transportation Systems, 2011, 12(4): 1511-1524. doi: 10.1109/TITS.2011.2160628 [19] VON LUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416. doi: 10.1007/s11222-007-9033-z [20] 马勇, 胡明华, 顾欣, 等. 基于谱聚类的终端区飞行轨迹分析[J]. 航空计算技术, 2015, 45(5): 46-50. doi: 10.3969/j.issn.1671-654X.2015.05.012MA Yong, HU Ming-hua, GU Xin, et al. Trajectory analysis in terminal area based on spectral clustering[J]. Aeronautical Computing Technique, 2015, 45(5): 46-50. (in Chinese). doi: 10.3969/j.issn.1671-654X.2015.05.012 [21] ANNONIR J, FORSTER C H Q. Analysis of aircraft trajectories using Fourier descriptors and kernel density estimation[C]//IEEE. 15th International IEEE Conference on Intelligent Transportation Systems. New York: IEEE, 2012: 1441-1446. [22] EUROCONTROL. European medium-term ATM network capacity plan assessment 2009-2012[R]. Brussels: EUROCONTROL, 2009. [23] 姚洪亮, 王秀芳, 王浩. 一种基于结构分解与因子分析的贝叶斯网络隐变量发现算法[J]. 计算机科学, 2012, 39(2): 244-249. doi: 10.3969/j.issn.1002-137X.2012.02.057YAO Hong-liang, WANG Xiu-fang, WANG Hao. Hidden variable discovering algorithm of Bayesian networks based on structural decomposition and factor analysis[J]. Computer Science, 2012, 39(2): 244-249. (in Chinese). doi: 10.3969/j.issn.1002-137X.2012.02.057 [24] 李琦, 姜桂艳, 杨聚芬. 基于因子分析与聚类分析的交通事件自动检测算法融合[J]. 吉林大学学报: 工学版, 2012, 42(5): 1191-1197. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201205021.htmLI Qi, JIANG Gui-yan, YANG Ju-fen. Automatic incident detecting algorithms fusion method based on factor analysis and cluster analysis[J]. Journal of Jilin University: Engineering and Technology Edition, 2012, 42(5): 1191-1197. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201205021.htm [25] PERNKOPF F, BOUCHAFFRA D. Genetic-based EMalgorithm for learning Gaussian mixture models[J]. IEEETransactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1344-1348. -






 下载:
下载:











 下载:
下载: